Koshe Dekhi 15.1 Class 9

1. আমি কামালদের বাড়ির ছবি দেখি ও উত্তর খুঁজি।

কষে দেখি 15.1

(i) কামালদের বাগানের ক্ষেত্রফল হিসাব করে লিখি।

সমাধানঃ

কামালদের বাগানটি বর্গক্ষেত্রাকার অর্থাৎ, বাগানটির দৈর্ঘ্য ও প্রস্থ সমান।

আমরা জানি,

বর্গক্ষেত্রের ক্ষেত্রফল

= (বাহু × বাহু )

= (বাহু)²বর্গ একক

∴ বাগানটির ক্ষেত্রফল

= (20)²

= 400 বর্গমিটার

উত্তরঃ কামালদের বাগানের ক্ষেত্রফল 400 বর্গমিটার।

koshe dekhi 15.1 class 9

1. আমি কামালদের বাড়ির ছবি দেখি ও উত্তর খুঁজি।

কষে দেখি 15.1

(ii) প্রতি বর্গমিটারে 30 টাকা হিসাবে কামালদের বারান্দার মেঝে মেরামত করতে কত খরচ হবে হিসাব করে লিখি।

সমাধানঃ

কামালদের বারান্দাটি আয়তক্ষেত্রাকার যার

দৈর্ঘ্য = 10 মিটার ও প্রস্থ = 5 মিটার

আমরা জানি,

আয়তক্ষেত্রের ক্ষেত্রফল

= (দৈর্ঘ্য × প্রস্থ ) বর্গ একক

∴ বারান্দার ক্ষেত্রফল

= (10 × 5) বর্গমিটার

= 50 বর্গমিটার

এখন,

যেহেতু, 1 বর্গমিটার মেঝে মেরামত করতে খরচ হয় 30 টাকা

∴ 50 বর্গমিটার মেঝে মেরামত করতে খরচ হবে

= 30 × 50 টাকা

= 1500 টাকা

উত্তরঃ কামালদের বারান্দার মেঝে মেরামত করতে 1500 টাকা খরচ হবে।

koshe dekhi 15.1 class 9

1. আমি কামালদের বাড়ির ছবি দেখি ও উত্তর খুঁজি।

কষে দেখি 15.1

(iii) কামাল তার পড়ার ঘরের মেঝেতে টালি বসাতে চায়। যদি প্রতিটি টালি 25 সেমি. × 25 সেমি. হয়, তবে তার পড়ার ঘরের মেঝেতে টালি বসাতে কতগুলি টালি লাগবে হিসাব করে লিখি।

সমাধানঃ

কামালদের পড়ার ঘরটি আয়তক্ষেত্রাকার যার

দৈর্ঘ্য = 6 মিটার ও প্রস্থ = 5 মিটার

আমরা জানি,

আয়তক্ষেত্রের ক্ষেত্রফল

= (দৈর্ঘ্য × প্রস্থ ) বর্গ একক

∴ পড়ার ঘরের ক্ষেত্রফল

= (6 × 5) বর্গমিটার

= 30 বর্গ মিটার

= 300000 বর্গসেমি.

প্রতিটি টালির ক্ষেত্রফল

= 25 সেমি. × 25 সেমি.

= 625 বর্গসেমি.

∴ পড়ার ঘরের মেঝেতে টালি বসাতে লাগবে

$=\frac{300000}{625}$

= 480 টি

উত্তরঃ পড়ার ঘরের মেঝেতে টালি বসাতে 480 টি টালি লাগবে।

koshe dekhi 15.1 class 9

2. নীচের ছবি দেখি ও রঙিন অংশের ক্ষেত্রফল হিসাব করে লিখি।

(i)

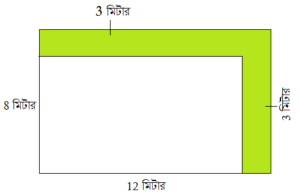
কষে দেখি 15.1

সমাধানঃ

উপরের ছবিটি আয়তক্ষেত্রাকার যার

দৈর্ঘ্য = 12 মিটার ও প্রস্থ = 8 মিটার

আমরা জানি,

আয়তক্ষেত্রের ক্ষেত্রফল

= (দৈর্ঘ্য × প্রস্থ) বর্গ একক

∴ আয়তক্ষেত্রাকার অংশটির ক্ষেত্রফল

= (12 × 8) বর্গমিটার

= 96 বর্গমিটার

উপরের ছবিতে রঙিন অংশটি দৈর্ঘ্যে ও প্রস্থে 3 মিটার করে চওড়া।

সুতরাং, রঙহীন অংশটির দৈর্ঘ্য = (12 − 3) মিটার = 9 মিটার

ও প্রস্থ = (8 − 3) মিটার = 5 মিটার

∴ রঙহীন অংশটির ক্ষেত্রফল

= 9 মিটার × 5 মিটার

= 45 বর্গমিটার

∴ রঙিন অংশের ক্ষেত্রফল

= সম্পূর্ণ চিত্রটির ক্ষেত্রফল − রঙহীন অংশটির ক্ষেত্রফল

= 96 বর্গমিটার − 45 বর্গমিটার

= 51 বর্গমিটার

উত্তরঃ নির্ণেয় রঙিন অংশটির ক্ষেত্রফল 51 বর্গমিটার।

koshe dekhi 15.1 class 9

2. নীচের ছবি দেখি ও রঙিন অংশের ক্ষেত্রফল হিসাব করে লিখি।

(ii)

কষে দেখি 15.1

সমাধানঃ

উপরের ছবিটি আয়তক্ষেত্রাকার যার

দৈর্ঘ্য = 26 মিটার ও প্রস্থ = 14 মিটার

আমরা জানি,

আয়তক্ষেত্রের ক্ষেত্রফল

= (দৈর্ঘ্য × প্রস্থ) বর্গ একক

∴ আয়তক্ষেত্রাকার অংশটির ক্ষেত্রফল

= (26 × 14) বর্গমিটার

= 364 বর্গমিটার

উপরের ছবিতে রঙিন অংশটির প্রতিটি প্রান্ত 3 মিটার করে চওড়া।

এখন, চিত্রটিতে রঙিন অংশটি বাদ দিলে চারটি সমান মাপের আয়তক্ষেত্র পাওয়া যায় যাদের প্রত্যেকের দৈর্ঘ্য

$=\frac{26-3}{2}$ মিটার

$=\frac{23}{2}$ মিটার

ও প্রস্থ

$=\frac{14-3}{2}$ মিটার

$=\frac{11}{2}$ মিটার

∴ প্রত্যেকটি আয়তক্ষেত্রের ক্ষেত্রফল

$= \frac{23}{2}\times \frac{11}{2}$ বর্গমিটার

$=\frac{253}{4}$ বর্গমিটার

∴ চিত্রটিতে রঙিন অংশটি বাদ দিলে যে চারটি সমান মাপের আয়তক্ষেত্র পাওয়া যায় তাদের মোট ক্ষেত্রফল

$=4\times \frac{253}{4}$ বর্গমিটার

= 253 বর্গমিটার

সুতরাং, রঙিন অংশের ক্ষেত্রফল

= সম্পূর্ণ চিত্রটির ক্ষেত্রফল − রঙহীন অংশটির ক্ষেত্রফল

= 364 বর্গমিটার − 253 বর্গমিটার

= 111 বর্গমিটার

উত্তরঃ নির্ণেয় রঙিন অংশটির ক্ষেত্রফল 111বর্গমিটার।

koshe dekhi 15.1 class 9

2. নীচের ছবি দেখি ও রঙিন অংশের ক্ষেত্রফল হিসাব করে লিখি।

(iii)

কষে দেখি 15.1

সমাধানঃ

উপরের ছবিটি আয়তক্ষেত্রাকার যার

দৈর্ঘ্য = (4 + 16 + 4) মিটার = 24 মিটার

ও প্রস্থ = (4 + 9 + 4) মিটার = 17 মিটার

আমরা জানি,

আয়তক্ষেত্রের ক্ষেত্রফল

= (দৈর্ঘ্য × প্রস্থ) বর্গ একক

∴ আয়তক্ষেত্রাকার অংশটির ক্ষেত্রফল

= (24 × 17) বর্গমিটার

= 408 বর্গমিটার

আবার, উপরের চিত্রে রঙহীন অংশটিও আয়তাকার যার

দৈর্ঘ্য = 16 মিটার ও প্রস্থ = 9 মিটার

∴ রঙহীন অংশটির ক্ষেত্রফল

= (16 × 9) বর্গমিটার

= 144 বর্গমিটার

সুতরাং, রঙিন অংশের ক্ষেত্রফল

= সম্পূর্ণ চিত্রটির ক্ষেত্রফল − রঙহীন অংশটির ক্ষেত্রফল

= 408 বর্গমিটার − 144 বর্গমিটার

= 264 বর্গমিটার

উত্তরঃ নির্ণেয় রঙিন অংশটির ক্ষেত্রফল 264 বর্গমিটার।

koshe dekhi 15.1 class 9

2. নীচের ছবি দেখি ও রঙিন অংশের ক্ষেত্রফল হিসাব করে লিখি।

(iv)

কষে দেখি 15.1

সমাধানঃ

উপরের ছবিটি আয়তক্ষেত্রাকার যার

দৈর্ঘ্য = 28 মিটার ও প্রস্থ = 20 মিটার

আমরা জানি,

আয়তক্ষেত্রের ক্ষেত্রফল

= (দৈর্ঘ্য × প্রস্থ) বর্গ একক

∴ আয়তক্ষেত্রাকার অংশটির ক্ষেত্রফল

= (28 × 20) বর্গমিটার

= 560 বর্গমিটার

আবার, উপরের চিত্রে রঙহীন অংশটিও আয়তাকার যার

দৈর্ঘ্য = (28 − 3 − 3) মিটার = 22 মিটার

ও প্রস্থ = (20 − 3 − 3) মিটার = 14 মিটার

∴ রঙহীন অংশটির ক্ষেত্রফল

= (22 × 14) বর্গমিটার

= 308 বর্গমিটার

সুতরাং, রঙিন অংশের ক্ষেত্রফল

= সম্পূর্ণ চিত্রটির ক্ষেত্রফল − রঙহীন অংশটির ক্ষেত্রফল

= 560 বর্গমিটার − 308 বর্গমিটার

= 252 বর্গমিটার

উত্তরঃ নির্ণেয় রঙিন অংশটির ক্ষেত্রফল 252 বর্গমিটার।

koshe dekhi 15.1 class 9

2. নীচের ছবি দেখি ও রঙিন অংশের ক্ষেত্রফল হিসাব করে লিখি।

(v)

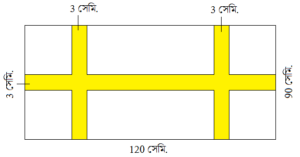
কষে দেখি 15.1

সমাধানঃ

সম্পূর্ণ চিত্রটির ক্ষেত্রফল

= 120 সেমি × 90 সেমি

= 10800 বর্গসেমি

রঙিন অংশ বাদে চিত্রটির দৈর্ঘ্য

= 120 − (3 + 3)

= 114 সেমি

ও প্রস্থ

= 90 − 3

= 87 সেমি

∴ রঙিন অংশ বাদে চিত্রটির ক্ষেত্রফল

= 114 সেমি × 87 সেমি

= 9918 বর্গসেমি

∴ রঙিন অংশের ক্ষেত্রফল

= সম্পূর্ণ চিত্রটির ক্ষেত্রফল − রঙিন অংশ বাদে চিত্রটির ক্ষেত্রফল

= (10800 − 9918) বর্গসেমি

= 882 বর্গসেমি

উত্তরঃ রঙিন অংশের ক্ষেত্রফল 882 বর্গসেমি।

koshe dekhi 15.1 class 9

3. বিরাটি মহাজাতি সঙ্ঘের আয়তাকার মাঠের দৈর্ঘ্য ও প্রস্থের অনুপাত 4:3 ; মাঠটির চারিদিকে একবার হেঁটে এলে 336 মিটার পথ অতিক্রম করা যায়। মাঠের ক্ষেত্রফল হিসাব করে লিখি।

সমাধানঃ

ধরি, আয়তাকার মাঠের দৈর্ঘ্য 4x একক ও প্রস্থ 3x একক।

∴ মাঠটির পরিসীমা

= 2 × (দৈর্ঘ্য + প্রস্থ ) একক

= 2 × (4x + 3x) একক

= 2 × 7x একক

= 14x একক

প্রশ্নানুসারে,

14x = 336

বা, $x=\frac{336}{14}$

∴ x = 24

সুতরাং, আয়তাকার মাঠের দৈর্ঘ্য = 4 × 24 = 96 একক

ও প্রস্থ = 3 × 24 = 72 একক।

∴ মাঠটির ক্ষেত্রফল

= দৈর্ঘ্য × প্রস্থ বর্গএকক

= 96 × 72 বর্গএকক

= 6912 বর্গএকক

উত্তরঃ আয়তাকার মাঠের ক্ষেত্রফল 6912 বর্গএকক।

koshe dekhi 15.1 class 9

4. প্রতি বর্গমিটারে 3.50 টাকা হিসাবে সমরদের একটি বর্গাকার জমি চাষ করতে খরচ হয় 1400 টাকা। প্রতি মিটারে 8.50 টাকা হিসাবে সমরদের জমিটির চারিধারে একই উচ্চতার তারের বেড়া দিতে কত খরচ হবে হিসাব করি।

সমাধানঃ

প্রতি বর্গমিটারে 3.50 টাকা হিসাবে সমরদের বর্গাকার জমি চাষ করতে 1400 টাকা খরচ হলে, জমিটির ক্ষেত্রফল

$=\frac{1400}{3.50}$

= 400 বর্গমিটার

∴ বর্গাকার জমির বাহুর দৈর্ঘ্য

$=\sqrt{400}$

= 20 মিটার

ও পরিসীমা

= 4 × বাহুর দৈর্ঘ্য

= 4 × 20

= 80 মিটার

এখন প্রতি মিটারে 8.50 টাকা হিসাবে সমরদের জমিটির চারিধারে একই উচ্চতার তারের বেড়া দিতে খরচ হবে

= 80 × 8.50

= 680 টাকা

উত্তরঃ সমরদের জমিটির চারিধারে তারের বেড়া দিতে 680 টাকা খরচ হবে।

koshe dekhi 15.1 class 9

5. সুহাসদের আয়তাকার জমির ক্ষেত্রফল 500 বর্গমিটার। জমিটির দৈর্ঘ্য 3 মিটার কমালে ও প্রস্থ 2 মিটার বাড়ালে জমিটি বর্গাকার হয়। সুহাসদের জমিটির দৈর্ঘ্য ও প্রস্থ হিসাব করে লিখি।

সমাধানঃ

দৈর্ঘ্য 3 মিটার কমিয়ে ও প্রস্থ 2 মিটার বাড়িয়ে যে বর্গক্ষেত্র তৈরি হয়, ধরি তার বাহুর দৈর্ঘ্য x মিটার।

∴ আয়তাকার জমিটির দৈর্ঘ্য = (x +3) মিটার ও প্রস্থ = (x −2) মিটার

প্রশ্নানুসারে,

(x +3) × (x −2) = 500

বা, x²− 2x + 3x − 6 = 500

বা, x²+ x − 6 − 500 = 0

বা, x²+ x − 506 = 0

বা, x²+ 23x − 22x − 506 = 0

বা, x (x + 23) − 22 (x + 23) = 0

বা, (x + 23) (x − 22) = 0

আমরা জানি, দুটি রাশির গুনফল শূন্য হলে তারা প্রত্যেকে পৃথক পৃথক ভাবে শূন্য হয়। সুতরাং,

(x + 23) = 0

∴ x = − 23

অথবা

(x − 22) = 0

∴ x = 22

যেহেতু বাহুর দৈর্ঘ্য ঋণাত্মক হয় না, তাই ঋণাত্মক মানটি অগ্রাহ্য করে পাই, x = 22

∴ আয়তাকার জমিটির দৈর্ঘ্য = (22 + 3) মিটার = 25 মিটার

ও প্রস্থ = (22−2) মিটার = 20 মিটার

উত্তরঃ সুহাসদের জমিটির দৈর্ঘ্য 25 মিটার ও প্রস্থ 25 মিটার।

koshe dekhi 15.1 class 9

6. আমাদের গ্রামের একটি বর্গাকার জমির প্রতিটি বাহুর দৈর্ঘ্য 300 মিটার। এই বর্গাকার জমির চারধার একই উচ্চতার 3 ডেসিমিটার চওড়া দেওয়াল দিয়ে ঘিরব। হিসাব করে দেখি প্রতি 100 বর্গমিটার জমিতে 5000 টাকা হিসাবে দেওয়ালের জন্য কত খরচ পড়বে।

সমাধানঃ

বর্গাকার জমির প্রতিটি বাহুর দৈর্ঘ্য 300 মিটার

∴ বর্গাকার জমির ক্ষেত্রফল

= (300)²বর্গমিটার

3 ডেসিমিটার

$=\frac{3}{10}$ মিটার

= 0.3 মিটার

রাস্তা বাদে জমিটির প্রতিটি বাহুর দৈর্ঘ্য

= 300 − (0.3 + 0.3) মিটার

= 299.4 মিটার

∴ রাস্তা বাদে জমিটির ক্ষেত্রফল

= (299.4)²বর্গমিটার

∴ রাস্তার ক্ষেত্রফল

= (300)²− (299.4)²

= (300 + 299.4) (300 −299.4) ${\color{Blue} \left [\because a^{2}-b^{2}=\left ( a+b \right )\left ( a-b \right ) \right ]}$

= 599.4 × 0.6

= 359.64 বর্গমিটার

100 বর্গমিটার জমিতে দেওয়াল দিতে খরচ হয় 5000 টাকা

1 বর্গমিটার জমিতে দেওয়াল দিতে খরচ হবে $=\frac{5000}{100}=50$ টাকা

∴ 359.64 বর্গমিটার জমিতে দেওয়াল দিতে খরচ হবে = 359.64 × 50 = 17982 টাকা

উত্তরঃ 359.64 বর্গমিটার জমিতে দেওয়াল দিতে খরচ হবে 17982 টাকা।

koshe dekhi 15.1 class 9

7. রেহানাদের আয়তাকার বাগানের দৈর্ঘ্য 14 মিটার এবং প্রস্থ 12 মিটার। বাগানটির ভিতরে চারিদিকে সমান চওড়া একটি রাস্তা তৈরি করতে প্রতি বর্গ মিটারে 20 টাকা হিসাবে মোট 1380 টাকা খরচ হলে, রাস্তাটি কত চওড়া হিসাব করে লিখি।

সমাধানঃ

ধরি, রাস্তাটি x মিটার চওড়া।

রাস্তাসহ আয়তাকার বাগানের ক্ষেত্রফল

= 14 মিটার × 12 মিটার

= 168 বর্গমিটার

রাস্তা বাদে বাগানের দৈর্ঘ্য = 14 −(x + x) মিটার = (14 − 2x) মিটার

এবং প্রস্থ = 12 −(x + x) মিটার = (12 − 2x) মিটার

∴ রাস্তা বাদে বাগানের ক্ষেত্রফল

= (14 − 2x) × (12 − 2x) বর্গমিটার

= (168 − 28x − 24x + 4x² )বর্গমিটার

= (168 − 52x + 4x²) বর্গমিটার

∴ রাস্তার ক্ষেত্রফল

= 168 − (168 − 52x + 4x²) বর্গমিটার

= 52x − 4x² বর্গমিটার

আবার, প্রতি বর্গ মিটারে 20 টাকা হিসাবে মোট 1380 টাকা খরচ হলে, রাস্তাটির ক্ষেত্রফল $=\frac{1380}{20}$ বর্গমিটার = 69 বর্গমিটার

প্রশ্নানুসারে,

52x − 4x²= 69

বা, 52x − 4x²− 69 = 0

বা, 4x²− 52x + 69 = 0

বা, 4x²− 46x − 6x + 69 = 0

বা, 2x (2x − 23) − 3(2x − 23) = 0

বা, (2x − 23) (2x − 3) = 0

(2x − 23) = 0

বা, 2x = 23

$\therefore x=\frac{23}{2}=11.5$

অথবা

(2x − 3) = 0

বা, 2x = 3

$\therefore x=\frac{3}{2}=1.5$

যেহেতু আয়তাকার বাগানের প্রস্থ 12 মিটার সুতরাং, বাগানটির ভিতরের চারিদিকে 11.5 মিটার চওড়া রাস্তা হওয়া সম্ভব না।

তাই, রাস্তাটি 1.5 মিটার চওড়া।

উত্তরঃ রাস্তাটি 1.5 মিটার চওড়া।

koshe dekhi 15.1 class 9

8. 1200 বর্গ সেমি ক্ষেত্রফল বিশিষ্ট একটি আয়তক্ষেত্রাকার জমির দৈর্ঘ্য 40 সেমি তার কর্ণের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি।

সমাধানঃ

আমরা জানি,

আয়তক্ষেত্রাকার জমির দৈর্ঘ্য × প্রস্থ = জমিটির ক্ষেত্রফল

বা, 40 × প্রস্থ = 1200

বা, প্রস্থ $=\frac{1200}{40}$

∴ প্রস্থ = 30 সেমি

আয়তক্ষেত্রাকার জমির কর্ণ

= √(দৈর্ঘ্য)²+ (প্রস্থ)²

$=\sqrt{\left ( 40 \right )^{2}+\left ( 30 \right )^{2}}$

$=\sqrt{1600+900}$

$=\sqrt{2500}$

= 50 সেমি

= বর্গক্ষেত্রের বাহুর দৈর্ঘ্য

∴ বর্গক্ষেত্রের ক্ষেত্রফল

= (50)²

= 2500 বর্গ সেমি

উত্তরঃ আয়তক্ষেত্রাকার জমির কর্ণের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল 2500 বর্গ সেমি।

koshe dekhi 15.1 class 9

9. একটি হল ঘরের দৈর্ঘ্য 6 মিটার, প্রস্থ 4 মিটার এবং উচ্চতা 4 মিটার। ঘরটিতে তিনটি দরজা আছে যাদের প্রত্যেকটি 1.5মি. × 1মি. এবং চারটি জানলা আছে যাদের প্রত্যেকটি 1.2মি. × 1মি.। ঘরটির চার দেওয়াল প্রতি বর্গমিটারে 70 টাকা হিসাবে রঙিন কাগজ দিয়ে ঢাকতে কত খরচ হবে ?

সমাধানঃ

দরজা, জানলা সমেত চার দেওয়ালের ক্ষেত্রফল = 2 (দৈর্ঘ্য + প্রস্থ) × উচ্চতা

= 2 (4 + 6) × 4

= 2 × 10 × 4

= 80 বর্গমিটার

তিনটি দরজার ক্ষেত্রফল

= 3 × (1.5 × 1) বর্গমিটার

= 4.5 বর্গমিটার

চারটি জানলার ক্ষেত্রফল

= 4 × (1.2 × 1) বর্গমিটার

= 4.8 বর্গমিটার

তিনটি দরজা ও চারটি জানলার মোট ক্ষেত্রফল

= 4.5 বর্গমিটার + 4.8 বর্গমিটার

= 9.3 বর্গমিটার

∴ দরজা ও জানলা বাদে চার দেওয়ালের ক্ষেত্রফল

= (80 − 9.3) বর্গমিটার

= 70.7 বর্গমিটার

∴ ঘরটির চার দেওয়াল প্রতি বর্গমিটারে 70 টাকা হিসাবে রঙিন কাগজ দিয়ে ঢাকতে খরচ হবে = (70.7 × 70) টাকা = 4949 টাকা

উত্তরঃ ঘরটির চার দেওয়াল প্রতি বর্গমিটারে 70 টাকা হিসাবে রঙিন কাগজ দিয়ে ঢাকতে 4949 টাকা খরচ হবে।

koshe dekhi 15.1 class 9

10. একটি ঘরের চার দেওয়ালের ক্ষেত্রফল 42 বর্গ মিটার এবং মেঝের ক্ষেত্রফল 12 বর্গ মিটার। ঘরটির দৈর্ঘ্য 4 মিটার হলে উচ্চতা হিসাব করে লিখি।

সমাধানঃ

ঘরটির দৈর্ঘ্য × প্রস্থ = মেঝের ক্ষেত্রফল

বা, 4 × প্রস্থ = 12

বা, প্রস্থ $=\frac{12}{4}$

∴ প্রস্থ = 3 মিটার

আমরা জানি,

ঘরের চার দেওয়ালের ক্ষেত্রফল = 2 (দৈর্ঘ্য + প্রস্থ) × উচ্চতা

আবার, প্রদত্ত ঘরের চার দেওয়ালের ক্ষেত্রফল 42 বর্গ মিটার

সুতরাং,

2 (দৈর্ঘ্য + প্রস্থ) × উচ্চতা = 42

বা, 2 (4 + 3) × উচ্চতা = 42

বা, 2 × 7 × উচ্চতা = 42

বা, 14 × উচ্চতা = 42

বা, উচ্চতা $=\frac{42}{14}$

∴ উচ্চতা = 3 মিটার

উত্তরঃ ঘরটির উচ্চতা 3 মিটার।

koshe dekhi 15.1 class 9

11. সুজাতা 84 বর্গ সেমি ক্ষেত্রফল বিশিষ্ট একটি আয়তকার কাগজে ছবি আঁকবে। কাগজটির দৈর্ঘ্য ও প্রস্থের অন্তর 5 সেমি। সুজাতার কাগজটির পরিসীমা হিসাব করি।

সমাধানঃ

ধরি, কাগজটির প্রস্থ x সেমি

∴ কাগজটির দৈর্ঘ্য = (x + 5) সেমি

প্রশ্নানুসারে,

x (x + 5) = 84

বা, x²+ 5x = 84

বা, x²+ 5x − 84 = 0

বা, x²+ 12x − 7x − 84 = 0

বা, x(x + 12) − 7(x + 12) = 0

বা, (x + 12) (x − 7) = 0

(x + 12) = 0

∴ x = − 12

অথবা

(x − 7) = 0

∴ x = 7

যেহেতু কাগজটির প্রস্থ ঋণাত্মক হয় না, তাই ঋণাত্মক মানটি অগ্রাহ্য করে পাই, x = 7

∴ আয়তাকার কাগজটির প্রস্থ = 7 সেমি

ও দৈর্ঘ্য = (7 + 5) সেমি= 12 সেমি

∴ সুজাতার কাগজটির পরিসীমা

= 2 (দৈর্ঘ্য + প্রস্থ)

= 2 (12 + 7)

= 2 × 19

= 38 সেমি

উত্তরঃ সুজাতার কাগজটির পরিসীমা 38 সেমি।

koshe dekhi 15.1 class 9

12. সিরাজদের বর্গাকার বাগানের বাইরের চারিদিকে 2.5 মিটার চওড়া একটি রাস্তা আছে। রাস্তাটির ক্ষেত্রফল 165 বর্গ মিটার। বাগানটির ক্ষেত্রফল ও কর্ণের দৈর্ঘ্য হিসাব করি। (√2 = 1.414)

সমাধানঃ

ধরি, বর্গাকার বাগানের প্রতিটি বাহুর দৈর্ঘ্য x মিটার।

∴ বাগানটির ক্ষেত্রফল = x² বর্গ মিটার

রাস্তাসহ বাগানটির প্রতিটি বাহুর দৈর্ঘ্য

= (x + 2 × 2.5) মিটার

= (x + 5) মিটার

∴ রাস্তাসহ বাগানটির ক্ষেত্রফল = (x + 5)²বর্গ মিটার

প্রশ্নানুসারে,

(x + 5)²− x²= 165

বা, x²+ 10x + 25 − x²= 165

বা, 10x + 25 = 165

বা, 10x = 165 − 25

বা, 10x = 140

∴ x = 14

∴ বাগানটির ক্ষেত্রফল = x² = 14²= 196 বর্গ মিটার

ও কর্ণের দৈর্ঘ্য

= √2 × x

= 1.414 × 14

= 19.796 মিটার।

উত্তরঃ সিরাজদের বর্গাকার বাগানটির ক্ষেত্রফল 196 বর্গ মিটার ও কর্ণের দৈর্ঘ্য 19.796 মিটার।

koshe dekhi 15.1 class 9

13. যে বর্গাকার জমির কর্ণের দৈর্ঘ্য 20√2 মিটার তার চারধার পাঁচিল দিয়ে ঘিরতে কত মিটার দৈর্ঘ্যের পাঁচিল দিতে হবে হিসাব করে লিখি। প্রতি বর্গ মিটারে 20 টাকা হিসাবে ঘাস বসাতে কত টাকা খরচ হবে হিসাব করে লিখি।

সমাধানঃ

ধরি, বর্গক্ষেত্রের বাহুর দৈর্ঘ্য x মিটার

আমরা জানি,

$x\sqrt{2}=20\sqrt{2}$

বা, $x=\frac{20\sqrt{2}}{\sqrt{2}}$

∴ x = 20 মিটার

∴ বর্গক্ষেত্রের পরিসীমা

= 4 × x

= 4 × 20

= 80 মিটার

এবং ক্ষেত্রফল

= x²বর্গ মিটার

= 20²

= 400 বর্গ মিটার

∴ প্রতি বর্গ মিটারে 20 টাকা হিসাবে ঘাস বসাতে খরচ হবে

= 20 × 400

= 8000 টাকা

উত্তরঃ বর্গাকার জমির চারধার পাঁচিল দিয়ে ঘিরতে 80 মিটার দৈর্ঘ্যের পাঁচিল দিতে হবে এবং প্রতি বর্গ মিটারে 20 টাকা হিসাবে ঘাস বসাতে 8000 টাকা খরচ হবে।

koshe dekhi 15.1 class 9

14. আমাদের আয়তাকার বাগানের একটি কর্ণ বরাবর একটি বেড়া দেব। আয়তাকার বাগানের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 12 মিটার ও 7 মিটার হলে বেড়ার দৈর্ঘ্য হিসাব করে দেখি। বেড়াটি আয়তাকার বাগানকে যে দুটি ত্রিভুজে ভাগ করবে তার পরিসীমা লিখি।

সমাধানঃ

প্রদত্ত,আয়তাকার বাগানের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 12 মিটার ও 7 মিটার

∴ আয়তাকার বাগানের কর্ণের দৈর্ঘ্য

= √(দৈর্ঘ্য)²+ (প্রস্থ)²

$=\sqrt{\left ( 12\right )^{2}+\left ( 7\right )^{2}}$

$=\sqrt{144+49}$

$=\sqrt{193}$ মিটার

অর্থাৎ, বেড়ার দৈর্ঘ্য $=\sqrt{193}$ মিটার (উত্তর)

এখন,বেড়াটি আয়তাকার বাগানকে যে দুটি ত্রিভুজে ভাগ করেছে তার পরিসীমা

$=\left ( 12+7+\sqrt{193} \right )$ মিটার

$=\left ( 19+\sqrt{193} \right )$ মিটার (উত্তর)

koshe dekhi 15.1 class 9

15. মৌসুমীদের বাড়ির আয়তাকার বড় হলঘরের দৈর্ঘ্য ও প্রস্থের অনুপাত 9:5 এবং পরিসীমা 140 মিটার। মৌসুমীরা হলঘরের মেঝেতে 25 সেমি. × 20 সেমি. আকারের আয়তাকার টালি বসাতে চায়। প্রতি 100 টালির দাম 500 টাকা হলে, মৌসুমীদের হলঘরের মেঝেতে টালি বসাতে কত খরচ হবে হিসাব করি।

সমাধানঃ

ধরি, হলঘরের দৈর্ঘ্য 9x মিটার ও প্রস্থ 5x মিটার

∴ হলঘরের পরিসীমা

2 (দৈর্ঘ্য + প্রস্থ) = 140

বা, 2 (9x + 5x) = 140

বা, 2 × 14x = 140

বা, 28x = 140

বা, $x=\frac{140}{28}$

∴ x = 5

∴ হলঘরের দৈর্ঘ্য = 9 × 5 = 45 মিটার ও প্রস্থ 5 × 5 = 25 মিটার

∴ হলঘরের মেঝের ক্ষেত্রফল

= দৈর্ঘ্য × প্রস্থ

= 45 মিটার × 25 মিটার

= 1125 বর্গ মিটার

= 11250000 বর্গ সেমি.

আয়তাকার টালির ক্ষেত্রফল

= 25 সেমি. × 20 সেমি.

= 500 বর্গ সেমি.

∴ মেঝেতে বসাতে টালি লাগবে

$=\frac{11250000}{500}$

= 22500 টি

এখন, প্রতিটি টালির মূল্য

$=\frac{500}{100}$

= 5 টাকা

∴ মৌসুমীদের হলঘরের মেঝেতে টালি বসাতে খরচ হবে

= 5 × 22500

= 112500 টাকা

উত্তরঃ মৌসুমীদের হলঘরের মেঝেতে টালি বসাতে 112500 টাকা খরচ হবে।

koshe dekhi 15.1 class 9

16. 18 মিটার দৈর্ঘ্য বিশিষ্ট একটি বড়াে হলঘর কার্পেট দিয়ে মুড়তে 2160 টাকা খরচ হয়। যদি হলঘরের প্রস্থ 4 মিটার কম হতাে তাহলে 1620 টাকা খরচ হতাে। হলঘরের ক্ষেত্রফল হিসাব করি।

সমাধানঃ

হলঘরের প্রস্থ 4 মিটার কম হওয়ার কারণে কার্পেট দিয়ে মুড়তে (2160 – 1620) টাকা অর্থাৎ, 540 টাকা কম খরচ হয়।

যেহেতু হলঘরের (এক্ষেত্রে হলঘরের মেঝের কথা বলা হয়েছে) দৈর্ঘ্য 18 মিটার এবং প্রস্থ 4 মিটার কম হয়, এই কারণে ক্ষেত্রফলের হ্রাস ঘটে (18 × 4) বর্গ মিটার।

∴ প্রতি বর্গমিটার ক্ষেত্রফল কার্পেট দিয়ে মুড়তে খরচ হয়

$=\frac{540}{18\times 4}$ টাকা।

= 7.5 টাকা।

প্রদত্ত, হলঘরের সম্পূর্ণটা কার্পেট দিয়ে মুড়তে মোট খরচ হয় = 2160 টাকা।

সুতরাং, হলঘরের ক্ষেত্রফল

$=\frac{2160}{7.5}$ বর্গ মিটার

= 288 বর্গ মিটার।

উত্তরঃ হলঘরের ক্ষেত্রফল 288 বর্গ মিটার।

koshe dekhi 15.1 class 9

17. একটি আয়তাকার জমির কর্ণের দৈর্ঘ্য 15 মিটার এবং দৈর্ঘ্য ও প্রস্থের অন্তর 3 মিটার। জমিটির পরিসীমা ও ক্ষেত্রফল নির্ণয় করি।

সমাধানঃ

ধরি, আয়তাকার জমির দৈর্ঘ্য x মিটার ও প্রস্থ (x − 3) মিটার

∴ আয়তাকার জমির কর্ণের দৈর্ঘ্য

$=\sqrt{x^{2}+\left ( x-3 \right )^{2}}$ মিটার

প্রশ্নানুসারে,

$\sqrt{x^{2}+\left ( x-3 \right )^{2}}= 15$

উভয়দিকে বর্গ করে পাই,

বা, $x^{2}+\left ( x-3 \right )^{2}= 225$

বা, x²+ x²− 6x + 9 − 225 = 0

বা, 2x²− 6x − 216 = 0

বা, x²− 3x − 108= 0

বা, x²− 12x + 9x − 108 = 0

বা, x (x − 12) + 9 (x − 12) = 0

বা, (x − 12) (x + 9) = 0

(x − 12) = 0

∴ x = 12

অথবা

(x + 9) = 0

∴ x = − 9

যেহেতু আয়তাকার জমির দৈর্ঘ্য ঋণাত্মক হয় না, তাই ঋণাত্মক মানটি অগ্রাহ্য করে পাই, x = 12

∴ আয়তাকার জমির দৈর্ঘ্য = 12 মিটার

ও প্রস্থ = (12 − 3) মিটার = 9 মিটার

∴ আয়তাকার জমির পরিসীমা

= 2 (দৈর্ঘ্য + প্রস্থ) মিটার

= 2 (12 + 9)

= 2 × 21

= 42 মিটার

ও ক্ষেত্রফল

= দৈর্ঘ্য × প্রস্থ

= 12 মিটার × 9 মিটার

= 108 বর্গ মিটার

উত্তরঃ আয়তাকার জমিটির পরিসীমা 42 মিটার ও ক্ষেত্রফল 108 বর্গ মিটার।

koshe dekhi 15.1 class 9

18. 385 মিটার × 60 মিটার পরিমাপের একটি আয়তাকার চাতাল পাকা করতে সর্ববৃহৎ কত মাপের বর্গাকার টাইলস ব্যবহার করা যাবে এবং সেক্ষেত্রে টাইলসের সংখ্যা কত হবে হিসাব করি।

সমাধানঃ

আয়তাকার চাতালটির দৈর্ঘ্য

= 385 মিটার

= 5 × 7 × 11 মিটার

ও প্রস্থ

= 60 মিটার

= 2 × 2 × 3 × 5 মিটার

∴ আয়তাকার চাতালটির দৈর্ঘ্য ও প্রস্থের গ.সা.গু = 5 মিটার

∴ সর্ববৃহৎ বর্গাকার টাইলস -এর মাপ হবে = 5 মিটার × 5 মিটার

এবং টাইলসের সংখ্যা হবে

$=\frac{385\times 60}{5\times 5}$

= 924 টি

উত্তরঃ আয়তাকার চাতাল পাকা করতে সর্ববৃহৎ 5 মিটার × 5 মিটার মাপের বর্গাকার টাইলস ব্যবহার করা যাবে এবং সেক্ষেত্রে টাইলসের সংখ্যা 924 টি হবে।

koshe dekhi 15.1 class 9

19. বহু বিকল্পীয় প্রশ্ন: (M.CQ)

(i) একটি বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য 12√2 সেমি.। বর্গক্ষেত্রটির ক্ষেত্রফল

(a) 28৪ বর্গ সেমি. (b) 144 বর্গ সেমি. (C) 72 বর্গ সেমি. (d) 18 বর্গ সেমি.

সমাধানঃ

ধরি, বর্গক্ষেত্রের বাহুর দৈর্ঘ্য x সেমি.

আমরা জানি,

$x\sqrt{2}=12\sqrt{2}$

বা, $x=\frac{12\sqrt{2}}{\sqrt{2}}$

∴ x = 12 সেমি.

∴ বর্গক্ষেত্রের ক্ষেত্রফল

= x²বর্গ সেমি.

= 12²

= 144 বর্গ সেমি.

উত্তরঃ (b) 144 বর্গ সেমি.

koshe dekhi 15.1 class 9

19. (ii) যদি একটি বর্গক্ষেত্রের ক্ষেত্রফল A₁ বর্গ একক এবং ওই বর্গক্ষেত্রের কর্ণের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল A₂ বর্গ একক হয়,তাহলে A₁ : A₂হবে

(a) 1:2 (b) 2:1 (C) 1:4 (d) 4:1

সমাধানঃ

ধরি, বর্গক্ষেত্রের বাহুর দৈর্ঘ্য x একক

বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য = x√2 একক

প্রশ্নানুসারে,

A₁= x²এবং

A₂= (x√2)² = 2x²

∴ A₁ : A₂

= x²: 2x²

= 1 : 2

উত্তরঃ (a) 1:2

koshe dekhi 15.1 class 9

19. (iii) 6 মিটার লম্বা ও 4 মিটার চওড়া একটি আয়তাকার জায়গা 2 ডেসিমি. বর্গ টালি দিয়ে বাঁধাতে হলে টালি লাগবে

(a) 1200 (b) 2400 (c) 600 (d) 1800

সমাধানঃ

আয়তাকার জায়গার দৈর্ঘ্য

= 6 মিটার

= 60 ডেসিমি

ও প্রস্থ

= 4 মিটার

= 40 ডেসিমি

আয়তাকার জায়গার ক্ষেত্রফল

= 60 ডেসিমি × 40 ডেসিমি

= 2400 বর্গডেসিমি

প্রতিটি টালির ক্ষেত্রফল

= 2 × 2

= 4 বর্গডেসিমি

∴ টালি লাগবে

$=\frac{2400}{4}$

= 600 টি

উত্তরঃ (c) 600

koshe dekhi 15.1 class 9

19. (iv) সমান পরিসীমাবিশিষ্ট একটি বর্গক্ষেত্র এবং একটি আয়তক্ষেত্রের ক্ষেত্রফল যথাক্রমে S এবং R হলে,

(a) S = R (b) S> R (c) s < R

সমাধানঃ

ধরি, বর্গক্ষেত্রের বাহুর দৈর্ঘ্য x একক

এবং আয়তক্ষেত্রটির দৈর্ঘ্য a একক ও প্রস্থ b একক

বর্গক্ষেত্রের ক্ষেত্রফল S = x²বর্গএকক ও পরিসীমা = 4x একক এবং আয়তক্ষেত্রের ক্ষেত্রফল R = ab বর্গএকক ও পরিসীমা = 2 (a + b) একক

প্রশ্নানুসারে,

4x = 2 (a + b)

বা, 2x = (a + b)

উভয়দিকে বর্গ করে পাই,

বা, 4x²= (a + b)²

বা, 4x²= (a − b)²+ 4ab

বা, 4S= (a − b)²+ 4R

বা, 4S− 4R = (a − b)²

বা, 4S− 4R > 0 [যেহেতু,(a − b)²>0]

বা, 4S > 4R

∴ S > R

উত্তরঃ (b) S> R

koshe dekhi 15.1 class 9

19. (v) একটি আয়তক্ষেত্রের কর্ণের দৈর্ঘ্য 10 সেমি. এবং ক্ষেত্রফল 62.5 বর্গ সেমি. হলে আয়তক্ষেত্রটির দৈর্ঘ্য ও প্রস্থের সমষ্টি

(a) 12 সেমি. (b) 15 সেমি. (C) 20 সেমি. (d) 25 সেমি.

সমাধানঃ

ধরি,আয়তক্ষেত্রটির দৈর্ঘ্য a সেমি ও প্রস্থ b সেমি

∴ আয়তক্ষেত্রটির কর্ণ $=\sqrt{a^{2}+b^{2}}$ সেমি এবং ক্ষেত্রফল = ab = 62.5 বর্গ সেমি

প্রশ্নানুসারে,

$\sqrt{a^{2}+b^{2}}=10$

বা, $a^{2}+b^{2}=100$

বা, $\left ( a+b \right )^{2}-2ab=100$

বা, $\left ( a+b \right )^{2}-2\times 62.5=100$

বা, $\left ( a+b \right )^{2}=100+125$

বা, $\left ( a+b \right )^{2}=225$

বা, $\left ( a+b \right )=\sqrt{225}$

∴ a + b = 15

আয়তক্ষেত্রটির দৈর্ঘ্য ও প্রস্থের সমষ্টি 15 সেমি.

উত্তরঃ (b) 15 সেমি.

koshe dekhi 15.1 class 9

20. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন :

(i) একটি বর্গক্ষেত্রের বাহুর দৈর্ঘ্য 10% বৃদ্ধি করলে বর্গক্ষেত্রটির ক্ষেত্রফল শতকরা কত বৃদ্ধি পাবে?

সমাধানঃ

ধরি, বর্গক্ষেত্রের বাহুর দৈর্ঘ্য x একক

∴ ক্ষেত্রফল = x²বর্গএকক

বাহুর দৈর্ঘ্য 10% বৃদ্ধি করলে নতুন বাহুর দৈর্ঘ্য হবে

$=x+x\times \frac{10}{100}$

$=x+\frac{x}{10}$

$=\frac{10x+x}{10}$

$=\frac{11x}{10}$ একক

∴ নতুন ক্ষেত্রফল হয়

$=\left (\frac{11x}{10} \right )^{2}$

$=\frac{121x^{2}}{100}$ বর্গএকক

∴ ক্ষেত্রফল বৃদ্ধি পায়

$=\frac{121x^{2}}{100}-x^{2}$ বর্গএকক

$=\frac{121x^{2}-100x^{2}}{100}$ বর্গএকক

$=\frac{21x^{2}}{100}$ বর্গএকক

∴ ক্ষেত্রফল শতকরা বৃদ্ধিপায়

$=\frac{\frac{21x^{2}}{100}}{x^{2}}\times 100%$

$=\frac{21x^{2}}{100\times x^{2}}\times 100%$

= 21%

উত্তরঃ বর্গক্ষেত্রটির ক্ষেত্রফল শতকরা 21% বৃদ্ধি পাবে।

koshe dekhi 15.1 class 9

20. (ii) একটি আয়তক্ষেত্রের দৈর্ঘ্য 10% বৃদ্ধি এবং প্রস্থ 10 % হ্রাস করা হলে ক্ষেত্রফল শতকরা কত বৃদ্ধি বা হ্রাস পাবে?

সমাধানঃ

ধরি,আয়তক্ষেত্রটির দৈর্ঘ্য x একক ও প্রস্থ y একক।

∴ ক্ষেত্রফল = xyবর্গএকক

আয়তক্ষেত্রটির দৈর্ঘ্য 10% বৃদ্ধি পেলে নতুন দৈর্ঘ্য হবে

$=x+x\times \frac{10}{100}$

$=x+\frac{x}{10}$

$=\frac{10x+x}{10}$

$=\frac{11x}{10}$ একক

আয়তক্ষেত্রটির প্রস্থ 10% হ্রাস পেলে নতুন প্রস্থ হবে

$=y-y\times \frac{10}{100}$

$=y-\frac{y}{10}$

$=\frac{10y-y}{10}$

$=\frac{9y}{10}$ একক

∴ নতুন ক্ষেত্রফল হয়

$=\frac{11x}{10}\times \frac{9y}{10}$

$=\frac{99xy}{100}$ বর্গএকক

∴ ক্ষেত্রফল হ্রাস পায়

$=xy-\frac{99xy}{100}$ বর্গএকক

$=\frac{100xy-99xy}{100}$ বর্গএকক

$=\frac{xy}{100}$ বর্গএকক

∴ ক্ষেত্রফল শতকরা হ্রাস পায়

$=\frac{\frac{xy}{100}}{xy}\times 100%$

$=\frac{xy}{100\times xy}\times 100%$

= 1%

উত্তরঃ আয়তক্ষেত্রটির ক্ষেত্রফল শতকরা 1% হ্রাস পাবে।

koshe dekhi 15.1 class 9

20. (iii) একটি আয়তক্ষেত্রের কর্ণের দৈর্ঘ্য 5 সেমি.। কর্ণদ্বয়ের ছেদবিন্দু থেকে আয়তক্ষেত্রের একটি প্রস্থের উপর লম্বের দৈর্ঘ্য 2 সেমি.। আয়তক্ষেত্রের প্রস্থের দৈর্ঘ্য কত?

সমাধানঃ

koshe dekhi 15.1 class 9

ধরি, ABCD আয়তক্ষেত্রের কর্ণ BD = 5 সেমি. এবং কর্ণদ্বয়ের ছেদবিন্দু O থেকে প্রস্থ AD এর ওপর অঙ্কিত লম্ব OP = 2 সেমি.

∴ AB = 2 × OP = 2 × 2 = 4 সেমি.

সমকোণী ত্রিভুজ ABD এর ক্ষেত্রে

আমরা জানি,

AD²= BD²− AB²

বা, AD²= 5²− 4²

বা, AD²= 25 − 16

বা, AD²= 9

বা, $AD=\sqrt{9}$

∴ AD = 3

উত্তরঃ আয়তক্ষেত্রের প্রস্থের দৈর্ঘ্য 3 সেমি.

koshe dekhi 15.1 class 9

20. (iv) একটি বর্গক্ষেত্রের কর্ণদ্বয়ের ছেদবিন্দু থেকে তার যেকোনাে বাহুর উপর অঙ্কিত লম্বের দৈর্ঘ্য 2√2 সেমি. হলে, বর্গক্ষেত্রটির প্রতিটি কর্ণের দৈর্ঘ্য কত?

সমাধানঃ

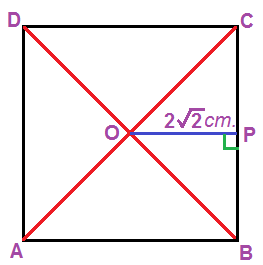
koshe dekhi 15.1 class 9

ABCD বর্গক্ষেত্রের কর্ণদ্বয়ের (AC ও BD) ছেদবিন্দু O থেকে তার যেকোনাে বাহুর উপর অঙ্কিত লম্বের দৈর্ঘ্য OP = 2√2 সেমি.

∴ বর্গক্ষেত্রের বাহুর দৈর্ঘ্য

= 2 × OP = 2 × 2√2= 4√2 সেমি.

∴ বর্গক্ষেত্রটির প্রতিটি কর্ণের দৈর্ঘ্য

= √2 × বর্গক্ষেত্রের বাহুর দৈর্ঘ্য

= √2 × 4√2

= 8 সেমি.

উত্তরঃ বর্গক্ষেত্রটির প্রতিটি কর্ণের দৈর্ঘ্য 8 সেমি.

koshe dekhi 15.1 class 9

20. (v) একটি আয়তক্ষেত্রের পরিসীমা 34 সেমি, এবং ক্ষেত্রফল 60 বর্গসেমি. আয়তক্ষেত্রের প্রতিটি কর্ণের দৈর্ঘ্য কত?

সমাধানঃ

ধরি,আয়তক্ষেত্রটির দৈর্ঘ্য x সেমি. ও প্রস্থ y সেমি.।

∴ ক্ষেত্রফল = xy = 60 বর্গসেমি.

এবং পরিসীমা 2 (x + y) = 34

বা, (x + y) = 17

উভয়দিকে বর্গ করে পাই,

বা, (x + y)² = 17²

বা, (x + y)² = 289

বা, x² + y² + 2xy = 289

বা, x² + y² + 2 × 60 = 289

বা, x² + y² + 120= 289

বা, x² + y² = 289 − 120

বা, x² + y² = 169

উভয়দিকে বর্গমূল করে পাই,

বা, $\sqrt{x^{2}+y^{2}}=\sqrt{169}$

$\therefore \sqrt{x^{2}+y^{2}}=13$

উত্তরঃ আয়তক্ষেত্রের প্রতিটি কর্ণের দৈর্ঘ্য 13 সেমি।

koshe dekhi 15.1 class 9

Support Me

If you appreciate my work and would like to support me, your contribution would be immensely valuable. Even a small amount can make a big difference in helping me grow my website.

You can donate via PhonePe, Paytm, or GPay using the details below:

Phone Number: 7980608289
UPI ID: 7980608289-2@ybl
Name: Prasanta Naskar

Thank you for your support!

and visit Our website : learningscience.co.in

গণিত প্রকাশ (দশম শ্রেণী) সম্পূর্ণ সমাধান

গণিত প্রকাশ (নবম শ্রেণী) সম্পূর্ণ সমাধান

গণিত প্রভা (ষষ্ঠ শ্রেণী) সম্পূর্ণ সমাধান

জীবন বিজ্ঞান (দশম শ্রেণী) (Life Science)

Thank You