Koshe dekhi 15.2 class 9
koshe dekhi 15.2 class 9
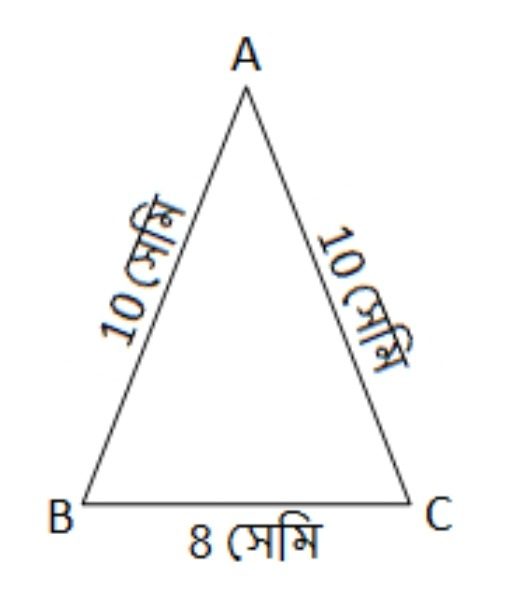
1. নীচের ছবিগুলির ক্ষেত্রের ক্ষেত্রফল হিসাব করে লিখি। সমাধানঃ ΔABC এর AB = BC = CA = 10 সেমি সুতরাং, ΔABC একটি সমবাহু ত্রিভুজ। ∴ ΔABC এর ক্ষেত্রফল = 25√3 বর্গ সেমি (উত্তর) সমাধানঃ A বিন্দু থেকে BC এর ওপর AD লম্ব অঙ্কন করলাম। এখন সমকোণী ত্রিভুজ ABD এর AD2 = AB2 − BD2 ∴ AD = 2 √21 সেমি ∴ ΔABC এর ক্ষেত্রফল = 8√21 বর্গ সেমি (উত্তর) সমাধানঃ ট্রাপিজিয়াম ABCD এর ক্ষেত্রফল = 13.5 বর্গ সেমি (উত্তর) সমাধানঃ ট্রাপিজিয়াম ABCD এর ক্ষেত্রফল = 247.5 বর্গ সেমি (উত্তর) সমাধানঃ ΔADC একটি সমকোণী ত্রিভুজ যার AD2 = AC2 − DC2 বা, AD2 = (AC + DC) (AC − DC) বা, AD2 = (42+ 38) (42 − 38) বা, AD2 = 80 × 4 বা, ∴ AD = 8 √5 সেমি ∴ ABCD আয়তক্ষেত্রের ক্ষেত্রফল = দৈর্ঘ্য × প্রস্থ = DC × AD = 38 × 8 √5 = 304 √5 বর্গ সেমি (উত্তর)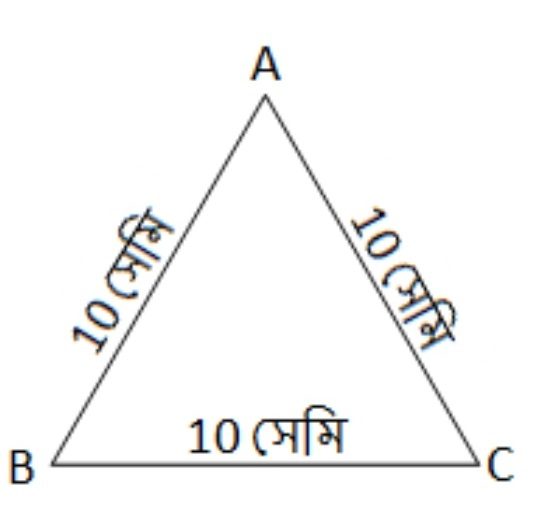
(বাহু)2
সেমি
× ভূমি × উচ্চতা
× সমান্তরাল বাহুদ্বয় এর যোগফল × সমান্তরাল বাহুদ্বয় এর মধ্যবর্তী দূরত্ব

× সমান্তরাল বাহুদ্বয় এর যোগফল × সমান্তরাল বাহুদ্বয় এর মধ্যবর্তী দূরত্ব

koshe dekhi 15.2 class 9
2. কোনাে সমবাহু ত্রিভুজের পরিসীমা 48 সেমি. হলে, তার ক্ষেত্রফল হিসাব করে লিখি। সমাধানঃ ধরি, সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য a সেমি. ∴ পরিসীমা = 3a সেমি. প্রশ্নানুসারে, 3a = 48 বা, ∴ a = 16 সেমি. ∴ সমবাহু ত্রিভুজ এর ক্ষেত্রফল = 64√3 বর্গ সেমি (উত্তর) (বাহু)2
koshe dekhi 15.2 class 9
3. ABC সমবাহু ত্রিভুজের উচ্চতা 5√3 সেমি. হলে, ত্রিভুজটির পরিসীমা ও ক্ষেত্রফল হিসাব করে লিখি। সমাধানঃ ধরি, সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য a সেমি. আমরা জানি, সমবাহু ত্রিভুজের উচ্চতা বা, ∴ a = 10 সেমি. ∴ ABC সমবাহু ত্রিভুজের পরিসীমা = 3a সেমি. = 3 × 10 = 30 সেমি. (উত্তর) ∴ ABC সমবাহু ত্রিভুজ এর ক্ষেত্রফল = 25√3 বর্গ সেমি (উত্তর) সেমি.
(বাহু)2
koshe dekhi 15.2 class 9
4. ΔABC সমদ্বিবাহু ত্রিভুজের সমান বাহুদুটির প্রত্যেকটির দৈর্ঘ্য 10 সেমি. এবং ভূমির দৈর্ঘ্য 4 সেমি. হলে, ΔABC -এর ক্ষেত্রফল হিসাব করে লিখি। সমাধানঃ A বিন্দু থেকে BC এর ওপর AD লম্ব অঙ্কন করলাম। এখন সমকোণী ত্রিভুজ ABD এর AD2 = AB2 − BD2 ∴ AD = 4 √6 সেমি ∴ ΔABC এর ক্ষেত্রফল = 8√6 বর্গ সেমি উত্তরঃ ΔABC -এর ক্ষেত্রফল 8√6 বর্গ সেমি। 
সেমি
× ভূমি × উচ্চতা
koshe dekhi 15.2 class 9
5. যদি কোনাে সমদ্বিবাহু ত্রিভুজের ভুমির দৈর্ঘ্য 12 সেমি. এবং সমান বাহুর প্রত্যেকটির দৈর্ঘ্য 10 সেমি. হয়, তবে ওই সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল হিসাব করে লিখি। সমাধানঃ A বিন্দু থেকে BC এর ওপর AD লম্ব অঙ্কন করলাম। এখন সমকোণী ত্রিভুজ ABD এর AD2 = AB2 − BD2 ∴ AD = 8 সেমি ∴ ΔABC এর ক্ষেত্রফল = 48 বর্গ সেমি উত্তরঃ সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল 48 বর্গ সেমি। 
সেমি
× ভূমি × উচ্চতা
koshe dekhi 15.2 class 9
6. কোনাে সমদ্বিবাহু ত্রিভুজের পরিসীমা 544 সেমি, এবং সমান বাহুর প্রত্যেকটির দৈর্ঘ্য ভূমির দৈর্ঘ্যের সমাধানঃ ধরি, সমদ্বিবাহু ত্রিভুজের ভূমির দৈর্ঘ্য x সেমি ∴ সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য প্রশ্নানুসারে, বা, বা, বা, ∴ x = 204 ∴ সমদ্বিবাহু ত্রিভুজের ভূমির দৈর্ঘ্য 204 সেমি এবং সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য = 170 সেমি A বিন্দু থেকে BC এর ওপর AD লম্ব অঙ্কন করলাম। এখন সমকোণী ত্রিভুজ ABD এর AD2 = AB2 − BD2 বা, AD2 = (AB + BD) (AB − BD) বা, AD2 = (170+ 102) (170 − 102) বা, AD2 = 272 × 68 বা, ∴ AD = 136 সেমি ∴ ΔABC এর ক্ষেত্রফল = 13872 বর্গ সেমি উত্তরঃ সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল 13872 বর্গ সেমি। অংশ; ত্রিভুজটির ক্ষেত্রফল হিসাব করে লিখি।

সেমি
সেমি
× ভূমি × উচ্চতা
koshe dekhi 15.2 class 9
7. একটি সমকোণী সমদ্বিবাহু ত্রিভুজের অতিভুজের দৈর্ঘ্য 12√2 সেমি. হলে, ত্রিভুজটির ক্ষেত্রফল হিসাব করে লিখি। সমাধানঃ ধরি, সমকোণী সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য x সেমি আমরা জানি, সমকোণী ত্রিভুজের ক্ষেত্রে, (ভূমি)2 + (লম্ব)2 = (অতি)2 বা, x2 + x2 = (12√2)2 বা, 2x2 = 288 বা, x2 = 144 বা, ∴ x = 12 সেমি ∴ সমকোণী সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল = 72 বর্গ সেমি উত্তরঃ সমকোণী সমদ্বিবাহু ত্রিভুজের ক্ষেত্রফল 72 বর্গ সেমি। × ভূমি × উচ্চতা
koshe dekhi 15.2 class 9
8.পৃথা একটি সামান্তরিক এঁকেছে যার কর্ণদ্বয়ের দৈর্ঘ্য যথাক্রমে 6 সেমি. ও 8 সেমি. এবং কর্ণদ্বয়ের মধ্যবর্তী কোণগুলির প্রত্যেকটি 90°; সামান্তরিকের বাহুগুলির দৈর্ঘ্য লিখি ও সামান্তরিকটির বৈশিষ্ট্য লিখি। সমাধানঃ যেহেতু, সামান্তরিকটির কর্ণদ্বয়ের দৈর্ঘ্য ভিন্ন এবং তারা পরস্পরকে সমকোণে সমদ্বিখন্ডিত করে সুতরাং, সামান্তরিকটি একটি রম্বস। ABCD একটি সামান্তরিক যার কর্ণদ্বয় AC = 6 সেমি. ও BD = 8 সেমি. পরস্পর P বিন্দুতে ছেদ করবে। ∴ সমকোণী ত্রিভুজ APB এর AP = 3 সেমি. ও BP = 4 সেমি. আমরা জানি, সমকোণী ত্রিভুজের ক্ষেত্রে, (AB)2 = (AP)2 + (BP)2 বা, (AB)2 = (3)2 + (4)2 বা, (AB)2 = 9 + 16 বা, (AB)2 = 25 বা, ∴ AB = 5 সেমি. উত্তরঃ সামান্তরিকের বাহুগুলির প্রত্যেকটির দৈর্ঘ্য 5 সেমি. এবং সামান্তরিকটি একটি রম্বস। 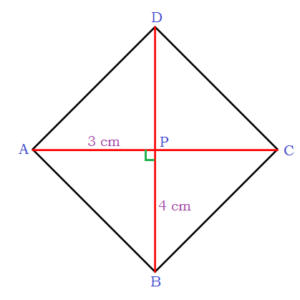
koshe dekhi 15.2 class 9
koshe dekhi 15.2 class 9
9. আমাদের পাড়ার ত্রিভুজাকৃতি একটি পার্কের বাহুগুলির দৈর্ঘ্যের অনুপাত 2:3:4; পার্কটির পরিসীমা 216 মিটার। (i) হিসাব করে পার্কটির ক্ষেত্রফল লিখি। (i) পার্কটির বৃহত্তম বাহুর বিপরীত কৌণিক বিন্দু থেকে ওই বাহুতে সােজাসুজি যেতে কত পথ হাঁটতে হবে হিসাব করে লিখি। সমাধানঃ ধরি, ত্রিভুজাকৃতি পার্কের বাহুগুলির দৈর্ঘ্য যথাক্রমে 2x মিটার, 3x মিটার এবং 4x মিটার। প্রশ্নানুসারে, 2x + 3x + 4x = 216 বা, 9x = 216 বা, ∴ x = 24 ∴ ত্রিভুজাকৃতি পার্কের বাহুগুলির দৈর্ঘ্য যথাক্রমে 2x মিটার = 2 × 24 = 48 মিটার = (ধরি a) , 3x মিটার = 3 × 24 = 72 মিটার = (ধরি b) এবং 4x মিটার = 4 × 24 = 96 মিটার = (ধরি c) ত্রিভুজটির প্রত্যেকটি বাহুর দৈর্ঘ্য ভিন্ন সুতরাং, ত্রিভুজটি বিষমবাহু ত্রিভুজ। এখন, পার্কটির অৰ্ধপরিসীমা ∴ ত্রিভুজটির ক্ষেত্রফল ধরি, পার্কটির বৃহত্তম বাহুর বিপরীত কৌণিক বিন্দু থেকে ওই বাহুতে সােজাসুজি যেতে p মিটার পথ হাঁটতে হবে। সুতরাং, বা, বা, উত্তরঃ (i) পার্কটির ক্ষেত্রফল (ii) পার্কটির বৃহত্তম বাহুর বিপরীত কৌণিক বিন্দু থেকে ওই বাহুতে সােজাসুজি যেতে মিটার
[যেখানে, a, b, c ত্রিভুজের বাহু ]
বর্গ মিটার
বর্গ মিটার।
মিটার পথ হাঁটতে হবে।
koshe dekhi 15.2 class 9
koshe dekhi 15.2 class 9
10. পহলমপুর গ্রামের ত্রিভুজাকৃতি মাঠের তিনদিকের দৈর্ঘ্য যথাক্রমে 26 মিটার, 28 মিটার ও 30 মিটার। (i) প্রতি বর্গমিটারে 5 টাকা হিসাবে ত্রিভুজাকৃতি মাঠে ঘাস লাগাতে মােট কত টাকা খরচ হবে হিসাব করে লিখি। (ii) ওই ত্রিভুজাকৃতি মাঠে প্রবেশের গেট তৈরির জন্য 5 মিটার জায়গা ছেড়ে বাকি চারধার বেড়া দিয়ে ঘিরতে প্রতি মিটার 18 টাকা হিসাবে মােট কত টাকা খরচ হবে হিসাব করে লিখি। সমাধানঃ ত্রিভুজটির প্রত্যেকটি বাহুর দৈর্ঘ্য ভিন্ন সুতরাং, ত্রিভুজটি বিষমবাহু ত্রিভুজ। এখন, পার্কটির অৰ্ধপরিসীমা ∴ ত্রিভুজটির ক্ষেত্রফল = 14 × 3 × 4 × 2 = 336 বর্গ মিটার (i) 1 বর্গমিটার মাঠে ঘাস লাগাতে খরচ 5 টাকা ∴ 336 বর্গমিটার মাঠে ঘাস লাগাতে খরচ হবে = 5 × 336 = 1680 টাকা। (উত্তর) (ii) ত্রিভুজাকৃতি মাঠটির পরিসীমা = (26 + 28 + 30) মিটার = 84 মিটার মাঠে প্রবেশের গেট তৈরির জন্য 5 মিটার জায়গা ছেড়ে দিলে বাকি জায়গা পরে থাকবে = 84 মিটার − 5 মিটার = 79 মিটার ∴ 79 মিটার বেড়া দিয়ে ঘিরতে প্রতি মিটার 18 টাকা হিসাবে মােট খরচ হবে = (79 × 18) টাকা = 1442 টাকা (উত্তর) মিটার
[যেখানে, a, b, c ত্রিভুজের বাহু ]
koshe dekhi 15.2 class 9
11. শাকিল একটি সমবাহু ত্রিভুজ PQR এঁকেছে। আমি ওই সমবাহু ত্রিভুজের অন্তঃস্থ কোনাে বিন্দু থেকে ত্রিভুজের বাহুগুলির উপর তিনটি লম্ব অঙ্কন করেছি যাদের দৈর্ঘ্য যথাক্রমে 10 সেমি., 12 সেমি. ও 8 সেমি। হিসাব করে ΔPQR-এর ক্ষেত্রফল লিখি। সমাধানঃ ধরি, সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য a সেমি. এবং অন্তঃস্থ বিন্দু O থেকে ত্রিভুজের বাহুগুলির উপর তিনটি লম্ব যথাক্রমে OA = 10 সেমি., OB = 12 সেমি. ও OC = 8 সেমি. ∴ ΔPQR = ΔOPQ + ΔOQR + ΔOPR বা, বা, বা, বা, ∴ ΔPQR = 15a বর্গ সেমি আবার আমরা জানি, সমবাহু ত্রিভুজের ক্ষেত্রফল সুতারাং, বা, ∴ a = 20√3 সেমি. ∴ ত্রিভুজের ক্ষেত্রফল = 15 × 20√3 = 300√3 বর্গ সেমি. উত্তরঃ ΔPQR-এর ক্ষেত্রফল 300√3 বর্গ সেমি.। বর্গ সেমি
koshe dekhi 15.2 class 9
12. একটি সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য 20 সেমি. এবং ওই বাহুদ্বয়ের অন্তর্ভুক্ত কোণ 45° হলে, ত্রিভুজটির ক্ষেত্রফল হিসাব করে লিখি। সমাধানঃ ধরি, ΔPQR-এর PQ = PR = 20 সেমি. এবং ∠QPR = 45° Q বিন্দু থেকে PR বাহুর ওপর QA লম্ব অঙ্কন করলাম। ∠PAQ = 90° ∴ সমকোণী ΔPAQ-এর বা, বা, ∴ QA = 10√2 সেমি. ∴ ΔPQR-এর ক্ষেত্রফল = 100√2 বর্গ সেমি. উত্তরঃ ΔPQR-এর ক্ষেত্রফল 100√2 বর্গ সেমি.।
koshe dekhi 15.2 class 9
13. একটি সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য 20 সেমি. এবং ওই বাহুদ্বয়ের অন্তর্ভুক্ত কোণ 30° হলে, ত্রিভুজটির ক্ষেত্রফল হিসাব করে লিখি। সমাধানঃ ধরি, ΔPQR-এর PQ = PR = 20 সেমি. এবং ∠QPR = 30° Q বিন্দু থেকে PR বাহুর ওপর QA লম্ব অঙ্কন করলাম। ∠PAQ = 90° ∴ সমকোণী ΔPAQ-এর বা, বা, ∴ QA = 10 সেমি. ∴ ΔPQR-এর ক্ষেত্রফল = 100 বর্গ সেমি. উত্তরঃ ΔPQR-এর ক্ষেত্রফল 100 বর্গ সেমি.।
koshe dekhi 15.2 class 9
14. একটি সমকোণী সমদ্বিবাহু ত্রিভুজের পরিসীমা (√2 +1) সেমি. হলে ত্রিভুজটির অতিভুজের দৈর্ঘ্য ও ক্ষেত্রফল হিসাব করে লিখি। সমাধানঃ ধরি, সমকোণী সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য a সেমি. আমরা জানি, সমকোণী ত্রিভুজের ক্ষেত্রে, (অতিভুজ)2 = (লম্ব)2 + (ভূমি)2 বা, (অতিভুজ)2 = (a)2 + (a)2 বা, (অতিভুজ)2 = 2a2 বা, অতিভুজ ∴ অতিভুজ = a√2 প্রশ্নানুসারে, a + a + a√2 = √2 + 1 বা, 2a + a√2 = √2 + 1 বা, a√2 (√2 + 1) = (√2 + 1) বা, a√2 = 1 ∴ অতিভুজ = a√2 ও ত্রিভুজটির ক্ষেত্রফল = 0.25 বর্গ সেমি. উত্তরঃ ত্রিভুজটির অতিভুজের দৈর্ঘ্য 1 সেমি. ও ক্ষেত্রফল 0.25 বর্গ সেমি.। = 1 সেমি.
koshe dekhi 15.2 class 9
15. মারিয়া ঘন্টায় 18 কিমি. বেগে সাইকেল চালিয়ে 10 মিনিটে একটি সমবাহু ত্রিভুজাকার মাঠের পরিসীমা বরাবর ঘুরে এল। ত্রিভুজটির একটি কৌণিক বিন্দু থেকে বিপরীত বাহুর মধ্যবিন্দু পর্যন্ত সােজা যেতে মারিয়ার কত সময় লাগবে হিসাব করে লিখি (√3 ≈ 1.732) সমাধানঃ 1 ঘন্টা = 60 মিনিট 18 কিমি. = 18 × 1000 = 18000 মিটার মারিয়া 60 মিনিটে যায় 18000 মিটার 1 মিনিটে যায় ∴ 10 মিনিটে যায় ∴ সমবাহু ত্রিভুজাকার মাঠের পরিসীমা 3000 মিটার ∴ ত্রিভুজটির প্রতিটি বাহুর দৈর্ঘ্য = 1000 মিটার এখন সমবাহু ত্রিভুজের উচ্চতা = 500√3 = 500 × 1.732 = 866 মিটার (প্রায়) ∴ ত্রিভুজটির একটি কৌণিক বিন্দু থেকে বিপরীত বাহুর মধ্যবিন্দু পর্যন্ত দূরত্ব 866 মিটার (প্রায়) মারিয়া 18000 মিটার যায় 60 মিনিটে 1 মিটার যায় ∴ 866 মিটার (প্রায়) যায় উত্তরঃ ত্রিভুজটির একটি কৌণিক বিন্দু থেকে বিপরীত বাহুর মধ্যবিন্দু পর্যন্ত সােজা যেতে মারিয়ার প্রায় 2.89 মিনিট সময় লাগবে। মিটার
মিটার
বাহুর দৈর্ঘ্য
মিনিটে
মিনিটে (প্রায়)
16. একটি সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য 1 মিটার বৃদ্ধি করলে ত্রিভুজটির ক্ষেত্রফল √3 বর্গমিটার বৃদ্ধি পায়। সমবাহু ত্রিভুজটির বাহুর দৈর্ঘ্য হিসাব করে লিখি। সমাধানঃ ধরি, সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য a মিটার আমরা জানি, সমবাহু ত্রিভুজের ক্ষেত্রফল সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য 1 মিটার বৃদ্ধি করলে নতুন ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য হবে = (a + 1) মিটার ∴ নতুন ক্ষেত্রফল হবে প্রশ্নানুসারে, বা, বা, বা, 2a + 1 = 4 বা, 2a = 4 − 1 বা, 2a = 3 বা, ∴ a = 1.5 উত্তরঃ সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য 1.5 মিটার। বর্গমিটার
বর্গমিটার
17. একটি সমবাহু ত্রিভুজ এবং বর্গক্ষেত্রের ক্ষেত্রফলের অনুপাত √3: 2; বর্গক্ষেত্রটির কর্ণের দৈর্ঘ্য 60 সেমি. হলে, সমবাহু ত্রিভুজটির পরিসীমা হিসাব করে লিখি। সমাধানঃ ধরি, সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য a সেমি. এবং বর্গক্ষেত্রের প্রতিটি বাহুর দৈর্ঘ্য x সেমি. আমরা জানি, সমবাহু ত্রিভুজের ক্ষেত্রফল ও বর্গক্ষেত্রের ক্ষেত্রফল = x2 বর্গসেমি. প্রশ্নানুসারে, বা, বা, বা, বা, a2 = 2x2 ∴ a = √2x বর্গক্ষেত্রটির কর্ণের দৈর্ঘ্য √2x = 60 সেমি. ∴ a = 60 সেমি. ∴ সমবাহু ত্রিভুজটির পরিসীমা = 3a = 3 × 60 = 180 সেমি. উত্তরঃ সমবাহু ত্রিভুজটির পরিসীমা 180 সেমি. বর্গসেমি.
18. একটি সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য এবং পরিসীমা যথাক্রমে 13 সেমি. এবং 30 সেমি.। ত্রিভুজটির ক্ষেত্রফল হিসাব করে লিখি। সমাধানঃ ধরি, সমকোণী ত্রিভুজের অপর দুটি বাহুর দৈর্ঘ্য x সেমি. ও y সেমি. অতিভুজের দৈর্ঘ্য 13 সেমি. এবং পরিসীমা 30 সেমি. হলে অপর দুটি বাহুর যোগফল (x + y) = 30 − 13 = 17 সেমি. আমরা জানি, সমকোণী ত্রিভুজের ক্ষেত্রে (লম্ব)2 + (ভূমি)2 = (অতি)2 বা, x2 + y2 = 132 বা, (x + y)2 − 2xy = 169 বা, (17)2 − 2xy = 169 বা, 289 − 2xy = 169 বা, − 2xy = 169 − 289 বা, − 2xy = − 120 ∴ xy = 60 ∴ ত্রিভুজটির ক্ষেত্রফল = 30 বর্গসেমি. উত্তরঃ ত্রিভুজটির ক্ষেত্রফল 30 বর্গসেমি. 60
19. একটি সমকোণী ত্রিভুজের সমকোণ সংলগ্ন বাহু দুটির দৈর্ঘ্য যথাক্রমে 12 সেমি. এবং 5 সেমি.। সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্বের দৈর্ঘ্য হিসাব করে লিখি (3 দশমিক স্থান পর্যন্ত আসন্নমান) সমাধানঃ আমরা জানি, সমকোণী ত্রিভুজের ক্ষেত্রে (অতি)2 = (লম্ব)2 + (ভূমি)2 বা, (অতি)2 = (12)2 + (5)2 বা, (অতি)2 = 144 + 25 বা, (অতি)2 = 169 ∴ অতিভুজ = 13 সেমি. ∴ ত্রিভুজটির ক্ষেত্রফল = 30 বর্গসেমি. ধরি, সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্বের দৈর্ঘ্য x সেমি. সুতরাং, বা, ∴ x = 4.615 সেমি. (প্রায়) উত্তরঃ সমকৌণিক বিন্দু থেকে অতিভুজের উপর লম্বের দৈর্ঘ্য প্রায় 4.615 সেমি.
20. 3 সেমি, 4 সেমি, ও 5 সেমি, দৈর্ঘ্যের বাহুবিশিষ্ট একটি সমকোণী ত্রিভুজাকার ক্ষেত্র থেকে একটি সর্ববৃহৎ বর্গাকারক্ষেত্র এমনভাবে কেটে নেওয়া হলাে যার একটি শীর্ষবিন্দু ত্রিভুজটির অতিভুজের ওপর অবস্থিত। বর্গাকারক্ষেত্রটির বাহুর দৈর্ঘ্য হিসাব করে লিখি। সমাধানঃ ধরি, সমকোণী ত্রিভুজ ABC AB = 4 সেমি. , BC = 3 সেমি. এবং AC = 5 সেমি. সমকোণী ত্রিভুজাকার ক্ষেত্র থেকে একটি সর্ববৃহৎ বর্গাকারক্ষেত্র BDEF কেটে নেওয়া হল যার একটি শীর্ষবিন্দু E ত্রিভুজটির অতিভুজ AC এর ওপর অবস্থিত। ধরি, বর্গক্ষেত্রের বাহুর দৈর্ঘ্য x সেমি অর্থাৎ, BD = DE = EF = FB = x সেমি ∴ AF = AB − FB = (4 − x) সেমি, DC = BC − BD = (3 − x) সেমি এখন, ΔAFE + বর্গক্ষেত্র BDEF + ΔDCE = ΔABC বা, বা, বা, বা, বা, 4x − x2 + 2x2 + 3x − x2 = 12 বা, 7x − 2x2 + 2x2 = 12 বা, 7x = 12 বা, উত্তরঃ বর্গাকারক্ষেত্রটির বাহুর দৈর্ঘ্য সেমি।
21. বহু বিকল্পীয় প্রশ্ন: (M.C.Q.) (i) একটি সমবাহু ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য 4 সেমি. হলে ত্রিভুজটির উচ্চতার পরিমাপ (a) 4√3 সেমি. (b) 16√3 সেমি. (C) ৪√3 সেমি. (d) 2√3 সেমি. সমাধানঃ সমবাহু ত্রিভুজের উচ্চতা = 2√3 সেমি. উত্তরঃ (d) 2√3 সেমি. বাহুর দৈর্ঘ্য
4
koshe dekhi 15.2 class 9
21. (ii) একটি সমকোণী সমদ্বিবাহু ত্রিভুজ যার সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য a একক। ত্রিভুজটির পরিসীমা (a) (1+√2)a একক (b) (2 + √2) a একক (c) 3a একক (d) (3 + 2√2)a একক সমাধানঃ আমরা জানি, সমকোণী ত্রিভুজের ক্ষেত্রে, (অতিভুজ)2 = (লম্ব)2 + (ভূমি)2 বা, (অতিভুজ)2 = (a)2 + (a)2 বা, (অতিভুজ)2 = 2a2 বা, অতিভুজ ∴ অতিভুজ = a√2 একক ∴ ত্রিভুজটির পরিসীমা = a + a + a√2 = 2a + a√2 = a(2 + √2) একক উত্তরঃ (b) (2 + √2) a একক
koshe dekhi 15.2 class 9
koshe dekhi 15.2 class 9
21. (iii) একটি সমবাহু ত্রিভুজের ক্ষেত্রফল, পরিসীমা এবং উচ্চতা যথাক্রমে a, s এবং h হলে, (a) 1 (b) সমাধানঃ ধরি, সমবাহু ত্রিভুজের দৈর্ঘ্য x একক। ∴ ত্রিভুজের ক্ষেত্রফল পরিসীমা s = 3x একক এবং উচ্চতা উত্তরঃ (C) এর মান
(C)
(d)
বর্গ একক,
একক
এর মান
koshe dekhi 15.2 class 9
21. (iv) একটি সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের দৈর্ঘ্য 5 সেমি. এবং ভূমির দৈর্ঘ্য 6 সেমি.। ত্রিভুজটির ক্ষেত্রফল (a) 18 বর্গসেমি, (b) 12 বর্গসেমি, (C) 15 বর্গসেমি. (d) 30 বর্গসেমি. সমাধানঃ A বিন্দু থেকে BC এর ওপর AD লম্ব অঙ্কন করলাম। এখন সমকোণী ত্রিভুজ ABD এর AD2 = AB2 − BD2 ∴ AD = 4 সেমি ∴ ΔABC এর ক্ষেত্রফল = 12 বর্গ সেমি উত্তরঃ (b) 12 বর্গসেমি সেমি
× ভূমি × উচ্চতা
koshe dekhi 15.2 class 9
21. (v) ABC ত্রিভুজের AC বাহুর উপর D এমন একটি বিন্দু যে AD : DC = 3 : 2; ABC ত্রিভুজের ক্ষেত্রফল 40 বর্গসেমি. হলে BDC ত্রিভুজের ক্ষেত্রফল (a) 16 বর্গসেমি, (b) 24 বর্গসেমি. (C) 30 বর্গসেমি. (d) 36 বর্গসেমি. সমাধানঃ যেহেতু, AD : DC = 3 : 2 ∴ 2 ΔABD = 3 ΔBDC আবার, ΔABD + ΔBDC = ΔABC বা, 2 ΔABD + 2 ΔBDC = 2 ΔABC বা, 3 ΔBDC + 2 ΔBDC = 2 ΔABC বা, 5 ΔBDC = 2 ΔABC বা, ΔBDC বা, ΔBDC ∴ ΔBDC = 16 বর্গসেমি উত্তরঃ (a) 16 বর্গসেমি ΔABC
koshe dekhi 15.2 class 9
21. (vi) একটি ত্রিভুজের অর্ধপরিসীমা থেকে প্রতিটির বাহুর দৈর্ঘ্যের অন্তর যথাক্রমে 8 সেমি, 7 সেমি. ও 5 সেমি.। ত্রিভুজটির ক্ষেত্রফল (a) 20√7 বর্গসেমি. (b) 10√14বর্গসেমি, (C) 20√14বর্গসেমি. (d) 140 বর্গসেমি. সমাধানঃ ধরি, ত্রিভুজের তিনটি বাহু যথাক্রমে a সেমি, b সেমি ও c সেমি এবং অর্ধপরিসীমা s সেমি। ∴ (s − a) = 8 সেমি., (s − b)= 7 সেমি. ও (s − c) = 5 সেমি. এখন, (s − a) + (s − b) + (s − c) = 8 + 7 + 5 বা, 3s − (a + b + c) = 20 বা, বা, বা, ∴ s = 20 ∴ ত্রিভুজটির ক্ষেত্রফল = 20√14 বর্গসেমি. উত্তরঃ (C) 20√14বর্গসেমি.
koshe dekhi 15.2 class 9
22. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন : (i) একটি সমবাহু ত্রিভুজের ক্ষেত্রফল ও উচ্চতার সাংখ্যমান সমান। ত্রিভুজের বাহুর দৈর্ঘ্য কত? সমাধানঃ ধরি, সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য a একক। প্রশ্নানুসারে, বা, ∴ a = 2 একক উত্তরঃ সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য 2 একক।
koshe dekhi 15.2 class 9
koshe dekhi 15.2 class 9
22. (ii) একটি ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য দ্বিগুণ করলে ত্রিভুজটির ক্ষেত্রফল শতকরা কত বৃদ্ধি হয়? সমাধানঃ ধরি, পূর্বে ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য ছিল যথাক্রমে a একক, b একক ও c একক এবং অর্ধপরিসীমা s একক ও ক্ষেত্রফল x বর্গ একক । ∴ ত্রিভুজটির ক্ষেত্রফল ছিল (x) এখন, ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য দ্বিগুণ করলে ত্রিভুজটির তিনটি বাহুর দৈর্ঘ্য হবে যথাক্রমে 2a একক, 2b একক ও 2c একক এবং অর্ধপরিসীমা 2s একক। ∴ নতুন ত্রিভুজটির ক্ষেত্রফল = 4x ∴ ত্রিভুজটির ক্ষেত্রফল শতকরা বৃদ্ধি হয় = 300 % উত্তরঃ ত্রিভুজটির ক্ষেত্রফল শতকরা 300% বৃদ্ধি হয়।
koshe dekhi 15.2 class 9
koshe dekhi 15.2 class 9
22. (iii) একটি ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য তিনগুণ করলে ত্রিভুজটির ক্ষেত্রফল শতকরা কত বৃদ্ধি হয়? সমাধানঃ ধরি, পূর্বে ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য ছিল যথাক্রমে a একক, b একক ও c একক এবং অর্ধপরিসীমা s একক ও ক্ষেত্রফল x বর্গ একক । ∴ ত্রিভুজটির ক্ষেত্রফল ছিল (x) এখন, ত্রিভুজের প্রতিটি বাহুর দৈর্ঘ্য দ্বিগুণ করলে ত্রিভুজটির তিনটি বাহুর দৈর্ঘ্য হবে যথাক্রমে 3a একক, 3b একক ও 3c একক এবং অর্ধপরিসীমা 3s একক। ∴ নতুন ত্রিভুজটির ক্ষেত্রফল = 9x ∴ ত্রিভুজটির ক্ষেত্রফল শতকরা বৃদ্ধি হয় = 800 % উত্তরঃ ত্রিভুজটির ক্ষেত্রফল শতকরা 800% বৃদ্ধি হয়।
koshe dekhi 15.2 class 9
koshe dekhi 15.2 class 9
22. (iv) একটি সমকোণী ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য (x-2) সেমি, x সেমি. এবং (x+2) সেমি.। ত্রিভুজটির অতিভুজের দৈর্ঘ্য কত? সমাধানঃ সমকোণী ত্রিভুজের বৃহত্তম বাহুটি হল (x+2) সেমি.। সমকোণী ত্রিভুজের ক্ষেত্রে, (x − 2)2 + x2 = (x + 2)2 বা, x2 − 4x + 4 + x2 = x2 + 4x + 4 বা, 2x2 − 4x + 4 − x2 − 4x − 4 = 0 বা, x2 − 8x = 0 বা, x(x − 8) = 0 ∴ হয় x = 0 অথবা, (x − 8) = 0 ∴ x = 8 ∴ ত্রিভুজটির অতিভুজের দৈর্ঘ্য = (8 + 2) সেমি. = 10 সেমি. উত্তরঃ ত্রিভুজটির অতিভুজের দৈর্ঘ্য 10 সেমি.
koshe dekhi 15.2 class 9
koshe dekhi 15.2 class 9
22. (v) একটি সমবাহু ত্রিভুজের উচ্চতার উপর একটি বর্গক্ষেত্র অঙ্কন করা হলাে। ত্রিভুজ ও বর্গক্ষেত্রের ক্ষেত্রফলের অনুপাত কত? সমাধানঃ ধরি, সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য x একক। ∴ ত্রিভুজের উচ্চতা এবং ক্ষেত্রফল এখন, সমবাহু ত্রিভুজের উচ্চতার উপর একটি বর্গক্ষেত্র অঙ্কন করা হলাে। ∴ বর্গক্ষেত্রের বাহুর দৈর্ঘ্য এবং ক্ষেত্রফল ত্রিভুজ ও বর্গক্ষেত্রের ক্ষেত্রফলের অনুপাত = √3 : 3 = 1 : √3 উত্তরঃ ত্রিভুজ ও বর্গক্ষেত্রের ক্ষেত্রফলের অনুপাত 1 : √3 একক,
বর্গ একক
একক,
বর্গ একক
বর্গ একক
koshe dekhi 15.2 class 9
Support Me
If you like my work then you can Support me by contributing a small amount which will help me a lot to grow my Website. It’s a request to all of you. You can donate me through phone pay / Paytm/ Gpay on this number 7980608289 or by the link below :
and visit Our website : learningscience.co.in
গণিত প্রকাশ (দশম শ্রেণী) সম্পূর্ণ সমাধান
গণিত প্রকাশ (নবম শ্রেণী) সম্পূর্ণ সমাধান
গণিত প্রভা (ষষ্ঠ শ্রেণী) সম্পূর্ণ সমাধান

Very good
thank you