Koshe Dekhi 12 Class 9

Koshe Dekhi 12 Class 9

Q1. ABCD সামান্তরিকের AB এবং DC বাহুর মধ্যবিন্দু যথাক্রমে P এবং Q; প্রমান করি যে, APCQ চতুর্ভুজাকার ক্ষেত্রের ক্ষেত্রফল = ½ × ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল।

সমাধানঃ

বিশেষ নির্বচনঃ D বিন্দু দিয়ে AB বাহুর উপর DM লম্ব অঙ্কন করা হল যা AB বাহুকে M বিন্দুতে ছেদ করেছে।

প্রমাণ করতে হবে যে, APCQ চতুর্ভুজাকার ক্ষেত্রের ক্ষেত্রফল = ½ × ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল।

প্রমাণঃ ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল = AB × DM …..(1)

ABCD সামান্তরিকের AB এবং DC বাহুর মধ্যবিন্দু যথাক্রমে P এবং Q

∴ AP = ½ AB এবং QC = ½ DC

আবার, ABCD সামান্তরিকের  AB = DC

সুতরাং, AP = QC …..(2)

APCQ চতুর্ভুজের AP || QC  [∵ ABCD সামান্তরিকের AB || DC]

এবং AP = QC   [(2) নং থেকে পাই]

∴ APCQ একটি সামান্তরিক।

APCQ সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল

= AP × DM

= ½ AB × DM [∵ AP = ½ AB]

= ½ × ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল [(1) নং থেকে পাই]

∴ APCQ সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল = ½ × ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল [প্রমানিত]

---

Q2. ABCD রম্বসের AB এবং DC বাহুর মধ্যে দূরত্ব PQ এবং AD ও BC বাহুর মধ্যে দূরত্ব RS; প্রমান করি যে, PQ = RS

সমাধানঃ

বিশেষ নির্বচনঃ ABCD রম্বসের AB এবং DC বাহুর মধ্যে দূরত্ব PQ এবং AD ও BC বাহুর মধ্যে দূরত্ব RS.

প্রমান করতে হবে যে, PQ = RS

অঙ্কনঃ C, R; B, R; A, P ও B, P বিন্দুগুলি যোগ করলাম।

প্রমাণঃ ΔABP এবং রম্বস ABCD একই সমান্তরাল যুগল AB ও DC এর মধ্যে অবস্থিত৷

∴ ABCD রম্বসের ক্ষেত্রফল = ½ × ΔABP এর ক্ষেত্রফল ….(1)

ΔBRC এবং রম্বস ABCD একই সমান্তরাল যুগল BC ও AD এর মধ্যে অবস্থিত৷

∴ ABCD রম্বসের ক্ষেত্রফল = ½ × ΔBRC এর ক্ষেত্রফল  ….(2)

(1) নং ও (2) নং সমীকরণ তুলনা করে পাই –

ΔABP এর ক্ষেত্রফল = ΔBRC এর ক্ষেত্রফল

বা, ½ × AB × PQ= ½ × BC × RS

আবার, যেহেতু রম্বসের প্রতিটি বাহুর দৈর্ঘ্য সমান 

∴ AB = BC

সুতরাং, ½ × AB × PQ= ½ × AB × RS

∴ PQ = RS  [প্রমানিত]

---

Q3. ABCD সামান্তরিকের AB এবং DC বাহুর মধ্যবিন্দু যথাক্রমে P এবং Q; প্রমান করি যে, PBQD একটি সামান্তরিক এবং ΔPBC = ½ × সামান্তরিক PBQD.

সমাধানঃ

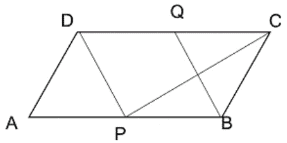
বিশেষ নির্বচনঃ ABCD সামান্তরিকের AB এবং DC বাহুর মধ্যবিন্দু যথাক্রমে P এবং Q;

প্রমান করতে হবে যে, PBQD একটি সামান্তরিক এবং ΔPBC = ½ × সামান্তরিক PBQD.

প্রমানঃ ABCD সামান্তরিকের AB = DC এবং AB || DC

P, AB বাহুর মধ্যবিন্দু

∴ PB = ½ AB

Q, DC বাহুর মধ্যবিন্দু

∴ DQ = ½ DC

সুতরাং, PB = DQ [যেহেতু, AB = DC]

যেহেতু, AB || DC

∴ PB || DQ

PBQD চতুর্ভুজের PB = DQ এবং PB || DQ

∴ PBQD একটি সামান্তরিক [প্রমানিত]

ΔPBC এবং সামান্তরিক PBQD একই ভূমি PB এবং একই সমান্তরাল সরলরেখাংশ যুগল PB ও CD এর মধ্যে অবস্থিত [যেহেতু, AB || DC, ∴ PB || DC] 

∴ ΔPBC = ½ × সামান্তরিক PBQD [প্রমানিত]

---

Q4. ABC সমদ্বিবাহু ত্রিভুজের AB = AC এবং বর্ধিত BC বাহুর উপর P যেকোনো একটি বিন্দু৷ P বিন্দু থেকে AB এবং AC বাহুর উপর যথাক্রমে PQ ও PR লম্ব৷ B বিন্দু থেকে AC বাহুর উপর লম্ব BS; প্রমান করি যে, PQ − PR = BS.

সমাধানঃ

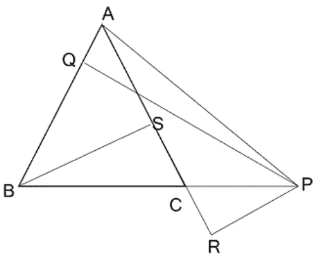
বিশেষ নির্বচনঃ ABC সমদ্বিবাহু ত্রিভুজের AB = AC. বর্ধিত BC বাহুর উপর P যেকোনো একটি বিন্দু। PQ⊥AB, PR⊥AC এবং BS⊥AC

প্রমাণ করতে হবে যে, PQ − PR = BS

অঙ্কনঃ A, P যুক্ত করলাম৷

প্রমানঃ ΔABC এর ক্ষেত্রফল

= ½ × ভূমি × উচ্চতা

= ½ × AC × BS

ΔACP এর ক্ষেত্রফল

= ½ × ভূমি × উচ্চতা

= ½ × AC × PR

ΔABP এর ক্ষেত্রফল

= ½ × ভূমি × উচ্চতা

= ½ × AB × PQ

ΔABP এর ক্ষেত্রফল = ΔABC এর ক্ষেত্রফল + ΔACP এর ক্ষেত্রফল

বা, ½ × AB × PQ = ½ × AC × BS + ½ × AC × PR

বা, AB × PQ = AC × BS + AC × PR

বা, AB × PQ = AC × (BS + PR) 

বা, AB × PQ = AB × (BS + PR) [∵ AB = AC]

বা, PQ = BS + PR

∴ PQ − PR = BS [প্রমানিত]

---

Q5. ABC সমবাহু ত্রিভুজের বাইরে এবং ABC কৌণিক অঞ্চলের মধ্যে O যেকোনো একটি বিন্দু৷ O বিন্দু থেকে AB, BC এবং CA বাহুর উপর লম্ব যথাক্রমে OP, OQ এবং OR; প্ৰমান করি যে, ত্রিভুজটির উচ্চতা = OP + OQ − OR

সমাধানঃ

বিশেষ নির্বচনঃ ABC একটি সমবাহু ত্রিভুজ। ABC কৌণিক অঞ্চলের মধ্যে O যেকোনো একটি বিন্দু। OP⊥AB, OQ⊥BC এবং OR⊥CA

প্রমাণ করতে হবে যে, ত্রিভুজটির উচ্চতা = OP + OQ − OR

অঙ্কনঃ AS⊥BC অঙ্কন করা হল এবং O,A; O,B এবং O, C যুক্ত করা হল।

প্রমানঃ ABC একটি সমবাহু ত্রিভুজ

সুতরাং, AB = BC = CA

ΔOAB এর ক্ষেত্রফল = ½ × AB × OP

ΔOBC এর ক্ষেত্রফল = ½ × BC × OQ

ΔOAC এর ক্ষেত্রফল = ½ × CA × OR

ΔABC এর ক্ষেত্রফল = ½ × BC × AS

ΔABC এর ক্ষেত্রফল = ΔOAB এর ক্ষেত্রফল + ΔOBC এর ক্ষেত্রফল − ΔOAC এর ক্ষেত্রফল

বা, ½ × BC × AS = ½ × AB × OP + ½ × BC × OQ − ½ × CA × OR

বা, BC × AS = AB × OP + BC × OQ − CA × OR

বা, BC × AS = BC × OP + BC × OQ − BC × OR [∵ AB = BC = CA]

বা, BC × AS = BC × (OP + OQ − OR)

বা, AS = OP + OQ − OR

∴ ত্রিভুজটির উচ্চতা = OP + OQ − OR [প্রমানিত]

---

Q6. ABCD সামান্তরিকের AB বাহুর সমান্তরাল সরলরেখা AD, AC এবং BC কে বা তাদের বর্ধিত অংশকে যথাক্রমে E, F ও G বিন্দুতে ছেদ করে৷ প্রমান করি যে, ΔAEG = ΔAFD

সমাধানঃ

বিশেষ নির্বচনঃ ABCD সামান্তরিকের AB বাহুর সমান্তরাল সরলরেখা AD, AC এবং BC কে যথাক্রমে E, F ও G বিন্দুতে ছেদ করে৷

প্রমাণ করতে হবে যে, ΔAEG = ΔAFD

প্রমানঃ ABCD একটি সামান্তরিক

সুতরাং, AB || DC এবং AD || BC

ABGE চতুর্ভুজের AB || EG এবং AE || BG  [∵ AD || BC]

সুতরাং, ABGE একটি সামান্তরিক।

EGCD চতুর্ভুজের DC || EG  [∵ AB || DC এবং AB || EG]

এবং ED || GC  [∵ AD || BC]

সুতরাং, EGCD একটি সামান্তরিক।

EGCD সামান্তরিক ও ΔCDF একই ভূমি ও একই সমান্তরাল সরলরেখা যুগল DC ও EG এর মধ্যে অবস্থিত

∴ EGCD সামান্তরিকের ক্ষেত্রফল = 2ΔCDF -এর ক্ষেত্রফল  …..(1)

যেহেতু সামান্তরিকের কর্ণ সামান্তরিককে দুটি সর্বসম ত্রিভুজে বিভক্ত করে।

∴ ABGE সামান্তরিক থেকে পাই ΔABG = ΔAEG

এবং ABCD সামান্তরিক থেকে পাই ΔABC = ΔADC

ABGE সামান্তরিকের ক্ষেত্রফল = ΔABG + ΔAEG

= ΔAEG + ΔAEG

= 2ΔAEG

∴ ABGE সামান্তরিকের ক্ষেত্রফল = 2ΔAEG  …..(2)

ABCD সামান্তরিকের ক্ষেত্রফল = EGCD সামান্তরিকের ক্ষেত্রফল + ABGE সামান্তরিকের ক্ষেত্রফল

ΔABC + ΔADC = 2ΔCDF + 2ΔAEG [(1) ও (2) -এর সাহায্যে]

বা, 2ΔADC = 2(ΔCDF + ΔAEG)

বা, ΔADC = ΔCDF + ΔAEG

বা, ΔAFD + ΔCDF = ΔCDF + ΔAEG

∴ ΔAEG = ΔAFD [প্রমানিত]

---

Q7. ABCD সামান্তরিকের DC বাহুর উপর E যেকোনো একটি বিন্দু। বর্ধিত AE, বর্ধিত BC কে F বিন্দুতে ছেদ করে। D, F যুক্ত করা হলো। প্রমাণ করি যে, (i) ΔADF = ΔABE (ii) ΔDEF = ΔBEC

সমাধানঃ

বিশেষ নির্বচন: ABCD সামান্তরিকের DC বাহুর উপর E যেকোনো একটি বিন্দু। বর্ধিত AE, বর্ধিত BC কে F বিন্দুতে ছেদ করে। D, F যুক্ত করা হলো।

প্রমাণ করতে হবে যে, (i) ΔADF = ΔABE (ii) ΔDEF = ΔBEC

প্রমানঃ ΔADF এবং সামান্তরিক ABCD একই ভূমি AD এবং একই সমান্তরাল সরলরেখাযুগল AD ও BF এর মধ্যে অবস্থিত।

সুতরাং, ΔADF = ½ × ABCD সামান্তরিকের ক্ষেত্রফল  ….(1)

ΔABE এবং সামান্তরিক ABCD একই ভূমি AD এবং একই সমান্তরাল সরলরেখাযুগল AD ও BF এর মধ্যে অবস্থিত ।

সুতরাং, ΔABE = ½ × ABCD সামান্তরিকের ক্ষেত্রফল  ….(2)

(1) নং ও ( 2 ) নং থেকে পাই,

ΔADF = ΔABE [(i) নং প্রমানিত]

ABCD সামান্তরিকের ক্ষেত্রফল = ΔADE + ΔABE + ΔBEC

(2) নং থেকে পাই,

ABCD সামান্তরিকের ক্ষেত্রফল = 2ΔABE

সুতরাং, 2ΔABE = ΔADE + ΔABE + ΔBEC

বা, 2ΔABE − ΔABE = ΔADE + ΔBEC

বা, ΔABE = ΔADE + ΔBEC

বা, ΔADF = ΔADE + ΔBEC  [(1) নং থেকে পাই]

বা, ΔADE + ΔDEF = ΔADE + ΔBEC

∴ ΔDEF = ΔBEC [(ii) নং প্রমানিত]

---

Q8. সমান ক্ষেত্রফলবিশিষ্ট ABC এবং ABD দুটি ত্রিভুজাকার ক্ষেত্রে AB বাহুর বিপরীত দিকে অবস্থিত। প্রমাণ করি যে, AB, CD – কে সমদ্বিখন্ডিত করে।

সমাধানঃ

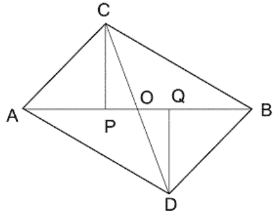
বিশেষ নির্বচনঃ ΔABC এবং ΔABD একই ভূমি AB এর ওপর বিপরীত দিকে অবস্থিত। ΔABC এবং ΔABD এর ক্ষেত্রফল সমান। CD সরলরেখা AB কে O বিন্দুতে ছেদ করেছে।

প্রমাণ করতে হবে যে, AB, CD কে সমদ্বিখন্ডিত করে।

অঙ্কনঃ CP⊥AB  ও  DQ⊥AB অঙ্কন করলাম।

প্রমানঃ ΔABC এর ক্ষেত্রফল = ½ × AB × CP

ΔABD এর ক্ষেত্রফল = ½ × AB × DQ

যেহেতু, ΔABC এবং ΔABD এর ক্ষেত্রফল সমান

সুতরাং, ½ × AB × CP = ½ × AB × DQ

∴ CP = DQ

ΔCPO ও ΔDQO এর –

∠OPC = ∠OQD [∵ CP⊥AB ও DQ⊥AB]

∠COP = ∠DOQ [পরস্পর বিপ্রতীপ কোণ]

CP = DQ

∴ ΔCPO ≅ ΔDQO [সর্বসমতার ΔAS শর্তানুসারে]

∴ CO = OD [সর্বসম ত্রিভুজের বিপরীত বাহু]

∴ O, CD বাহুর মধ্যবিন্দু

∴ AB, CD কে সমদ্বিখন্ডিত করে [প্রমানিত]

---

Q9. ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D; CDEF সামান্তরিকটি BC বাহু এবং A বিন্দু দিয়ে BC বাহুর সমান্তরাল সরলরেখার মধ্যে অবস্থিত৷ প্রমাণ করি যে, ΔABC = সামান্তরিক CDEF.

সমাধানঃ

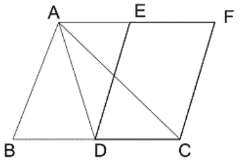
বিশেষ নির্বচনঃ ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D; CDEF সামান্তরিকটি BC বাহু এবং A বিন্দু দিয়ে BC বাহুর সমান্তরাল সরলরেখার মধ্যে অবস্থিত।

অঙ্কনঃ A, D যুক্ত করা হল।

প্রমানঃ ABC ত্রিভুজের D, BC বাহুর মধ্যবিন্দু

∴AD, ABC ত্রিভুজের মধ্যবিন্দু

∴ ΔADC = ½ × ΔABC …..(1)

ΔADC এবং DCFE সামান্তরিক একই ভূমি DC এবং একই সমান্তরাল সরলরেখা যুগল DC ও AF এর মধ্যে অবস্থিত।

∴ ΔADC = ½ × DCFE সামান্তরিকের ক্ষেত্রফল

(1) নং ও (2) নং থেকে পাই

ΔABC= সামান্তরিক CDEF [প্রমানিত]

---

Q10. ABCD সামান্তরিকের BD কর্ণের উপর P যেকোন একটি বিন্দু। প্রমাণ করি যে, ΔAPD = ΔCPD

সমাধানঃ

বিশেষ নির্বচনঃ ABCD সামান্তরিকের BD কর্ণের উপর P যেকোন একটি বিন্দু।

প্রমাণ করতে হবে যে, ΔAPD = ΔCPD

অঙ্কনঃ AE⊥BD ও CF⊥BD অঙ্কন করা হল

প্রমানঃ ΔABD এর ক্ষেত্রফল = ½ × BD × AE

ΔCBD এর ক্ষেত্রফল = ½ × BD × CF

আমরা জানি সামান্তরিকের কর্ণদ্বয় সামান্তরিককে দুটি সর্বসম ত্রিভুজে বিভক্ত করে।

∴ΔABD এর ক্ষেত্রফল = ΔCBD এর ক্ষেত্রফল

বা, ½ × BD × AE = ½ × BD × CF

∴ AE = CF

ΔAPD এর ক্ষেত্রফল = ½ × PD × AE

ΔCPD এর ক্ষেত্রফল = ½ × PD × CF

= ½ × PD × AE   [∵ AE = CF]

= ΔAPD এর ক্ষেত্রফল

∴ ΔAPD = ΔCPD [প্রমানিত]

---

Q11. ABC ত্রিভুজের AD এবং BE মধ্যমা৷ প্রমাণ করি যে, ΔACD = ΔBCE.

সমাধানঃ

বিশেষ নির্বচনঃ ABC ত্রিভুজের AD এবং BE মধ্যমা৷

প্রমাণ করতে হবে যে, ΔACD = ΔBCE

প্রমানঃ ΔABC এর AD মধ্যমা,

ΔABD =ΔACD [∵ ত্রিভুজের মধ্যমা ত্রিভুজটিকে দুটি সমান ক্ষেত্রফল বিশিষ্ট ত্রিভুজে বিভক্ত করে।]

∴ ΔACD = ½ × ΔABC  …. (1)

আবার, ΔABC এর BE মধ্যমা,

∴ ΔABE = ΔBCE

∴ ΔBCE = ½ × ΔABC  …..(2)

(1) নং ও (2) নং থেকে পাই,

ΔACD = ΔBCE [প্রমানিত]

---

Q12. ABC ত্রিভুজের BC বাহুর সমান্তরাল সরলরেখা AB এবং AC বাহুকে যথাক্রমে P এবং Q বিন্দুতে ছেদ করে৷ CP এবং BQ পরস্পরকে X বিন্দুতে ছেদ করে৷ প্রমাণ করি যে,

(i) ΔBPQ = ΔCPQ

(ii) ΔBCP = ΔBCQ

(iii) ΔACP = ΔABQ

(iv) ΔBXP = ΔCXQ

সমাধানঃ

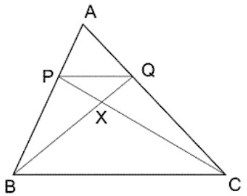
বিশেষ নির্বচনঃ ABC ত্রিভুজের P, AB বাহুর উপর এবং Q, AC বাহুর উপর যেকোনো একটি বিন্দু এবং BC || PQ; CP এবং BQ পরস্পরকে X বিন্দুতে ছেদ করে৷

প্রমাণ করতে হবে যে,

(i) ΔBPQ = ΔCPQ

(ii) ΔBCP = ΔBCQ

(iii) ΔACP = ΔABQ

(iv) ΔBXP = ΔCXQ

প্রমানঃ ΔBPQ ও ΔCPQ একই ভূমি PQ এবং একই সমান্তরাল সরলরেখাযুগল PQ এবং BC এর মধ্যে অবস্থিত।

∴ ΔBPQ = ΔCPQ [(i) নং প্রমানিত]

ΔBCP ও ΔBCQ একই ভূমি BC এবং একই সমান্তরাল সরলরেখাযুগল BC এবং PQ এর মধ্যে অবস্থিত।

∴ ΔBCP = ΔBCQ [(ii) নং প্রমানিত]

ΔABC = ΔACP + ΔBCP

আবার, ΔABC = ΔABQ + ΔBCQ

∴ ΔACP + ΔBCP = ΔABQ + ΔBCQ

বা, ΔACP + ΔBCP = ΔABQ + ΔBCP [∵ ΔBCP = ΔBCQ]

∴ ΔACP = ΔABQ [(iii) নং প্রমানিত]

যেহেতু, ΔBCP = ΔBCQ

বা, ΔBXP + ΔBCX = ΔCXQ + ΔBCX

∴ ΔBXP = ΔCXQ [(iv) নং প্রমানিত]

---

Q13. ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D এবং BC বাহুর উপর P যেকোন একটি বিন্দু৷ P, A যুক্ত করি৷ D বিন্দু দিয়ে PA সরলরেখাংশের সমান্তরাল সরলরেখা AB বাহুকে Q বিন্দুতে ছেদ করে৷

প্রমাণ করি যে, 

(i) ΔADQ = ΔPDQ

(ii) ΔBPQ = ½ × ΔABC

সমাধানঃ

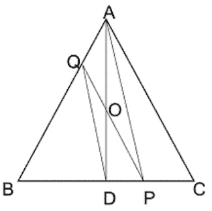
বিশেষ নির্বচনঃ

ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D এবং BC বাহুর উপর P যেকোন একটি বিন্দু P, A যুক্ত করি৷ D বিন্দু দিয়ে PA সরলরেখাংশের সমান্তরাল সরলরেখা AB বাহুকে Q বিন্দুতে ছেদ করে৷ AD ও PQ পরস্পরকে O বিন্দুতে ছেদ করেছে।

প্রমাণ করতে হবে যে,

(i) ΔADQ = ΔPDQ

(ii) ABPQ =½ × ΔABC

প্রমানঃ ΔADQ ও ΔPDQ একই ভূমি DQ এবং একই সমান্তরাল সরলরেখাযুগল DQ এবং PA এর মধ্যে অবস্থিত।

∴ ΔADQ = ΔPDQ [(i) নং প্রমানিত]

বা, ΔAOQ + ΔDOQ = ΔPOD + ΔDOQ

∴ ΔAOQ = ΔPOD

ΔBAD = ΔBQD + ΔAOQ + ΔDOQ

= ΔBQD + ΔPOD + ΔDOQ

= ΔBPQ

∴ ΔBAD = ΔBPQ …..(1)

ABC ত্রিভুজের AD মধ্যমা

∴ ΔBAD = ½ × ΔABC  ….(2)

(1) নং ও (2) নং থেকে পাই

ΔBPQ = ½ × ΔABC  [(ii) নং প্রমানিত]

---

Q14. ABC ত্রিভুজে AB = AC; B ও C বিন্দু থেকে AB ও AC বাহুর উপর লম্ব যথাক্রমে AC ও AB বাহুকে E ও F বিন্দুতে ছেদ করে৷ প্রমান করি যে, FE || BC.

সমাধানঃ

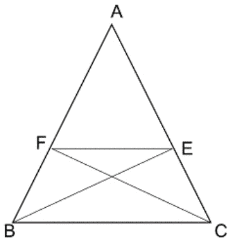
বিশেষ নির্বচনঃ ABC ত্রিভুজে AB = AC; CF⊥AB এবং BE⊥AC

প্রমাণ করতে হবে যে, FE || BC

প্রমানঃ ΔABC এর ক্ষেত্রফল = ½ × AB × CF

আবার ΔABC এর ক্ষেত্রফল = ½ × AC × BE

∴ ½ × AB × CF = ½ × AC × BE

∴ CF = BE [∵ AB = AC]

ΔBCF ও ΔBCE এর –

BC সাধারণ বাহু

∠BFC = ∠CEB [প্রত্যেকেই সমকোণ]

CF = BE

∴ ΔBCF ≅ ΔBCE [সর্বসমতার S-A-S শর্তানুসারে]

BE = CF [সর্বসম ত্রিভুজের অনুরূপ বাহু]

∴ ΔBCF = ΔBCE

ΔBCF ও ΔBCE এর ক্ষেত্রফল সমান এবং তারা একই ভূমি BC এর ওপর অবস্থিত।

∴ ΔBCF ও ΔBCE একই সমান্তরাল সরলরেখা যুগল BC ও FE এর মধ্যে অবস্থিত হবে।

সুতরাং, FE || BC [প্রমানিত]

---

Q15. ABC ত্রিভুজে ∠ABC = ∠ACB; ∠ABC ও ∠ACB কোণের সমদ্বিখন্ডকদ্বয় AC ও AB বাহুকে যথাক্রমে E ও F বিন্দুতে ছেদ করে৷ প্রমাণ করি যে, FE||BC.

সমাধানঃ

বিশেষ নির্বচনঃ ABC ত্রিভুজে ∠ABC =∠ACB; ∠ABC ও ∠ACB কোণের সমদ্বিখন্ডকদ্বয় AC ও AB বাহুকে যথাক্রমে E ও F বিন্দুতে ছেদ করে৷

প্রমাণ করতে হবে যে, FE || BC

প্রমানঃ BE, ∠ABC এর সমদ্বিখন্ডক

∴ ∠CBE = ½ ×∠ABC  …..(1)

CF, ∠ACB এর সমদ্বিখন্ডক

∠BCF = ½ × ∠ACB ….. (2)

আবার ∠ABC = ∠ACB

∴ ∠CBE =∠BCF …..(3) [(1) নং ও (2) নং থেকে পাই]

ΔBCF এবং ΔBCE এর –

∠CBE =∠BCF [(3) নং থেকে পাই]

∠FBC =∠ECB [∵ ∠ABC = ∠ACB]

BC সাধারণ বাহু

ΔBCF ≅ ΔBCE [সর্বসমতার A-A-S শর্তানুসারে]

∴ ΔBCF = ΔBCE

ΔBCF ও ΔBCE একই ভূমি BC এর ওপর অবস্থিত এবং এদের ক্ষেত্রফল সমান।

সুতরাং, ΔBCF ও ΔBCE একই সমান্তরাল যুগল BC ও FE এর মধ্যে অবস্থিত।

FE || BC [প্রমানিত]

---

Q16. সমান ক্ষেত্রফলবিশিষ্ট ABCD ও AEFG সামান্তরিক আকারের ক্ষেত্র দুটির ∠A সাধারণ এবং E, AB বাহুর উপর অবস্থিত। প্রমাণ করি যে, DE || FC.

সমাধানঃ

বিশেষ নির্বচনঃ ABCD সামান্তরিক ও AEFG সামান্তরিকের ক্ষেত্রফল সমান। ∠A সামান্তরিক দুটির সাধারণ কোণ। E, AB বাহুর উপর অবস্থিত।

প্রমাণ করতে হবে যে, DE||FC

অঙ্কনঃ D,F; E, C যুক্ত করা হল।

প্রমানঃ ΔDEF এবং সামান্তরিক AEFG একই ভূমি EF এবং একই সমান্তরাল সরলরেখা যুগল EF ও AG এর মধ্যে অবস্থিত।

সুতরাং, AEFG সামান্তরিকের ক্ষেত্রফল = 2ΔDEF

ΔCDE এবং সামান্তরিক ABCD একই ভূমি CD এবং একই সমান্তরাল সরলরেখা যুগল CD ও BA এর মধ্যে অবস্থিত।

সুতরাং, ABCD সামান্তরিকের ক্ষেত্রফল = 2ΔCDE

আবার, ABCD সামান্তরিকের ক্ষেত্রফল = AEFG সামান্তরিকের ক্ষেত্রফল

∴ 2ΔCDE = 2ΔDEF

∴ ΔCDE = ΔDEF

ΔCDE ও ΔDEF একই ভূমি DE এর উপর অবস্থিত এবং এদের ক্ষেত্রফল সমান

∴ ΔCDE ও ΔDEF একই সমান্তরাল সরলরেখা যুগল DE ও FC এর মধ্যে অবস্থিত হবে। 

∴ DE || FC  [প্রমানিত]

---

Q17. ABCD একটি সামান্তরিক এবং ABCE একটি চতুর্ভুজ৷ AC কৰ্ণ ABCE চতুর্ভুজ আকারের ক্ষেত্রটিকে দুটি সমান অংশে বিভক্ত করে৷ প্রমাণ করি যে, AC || DE

সমাধানঃ

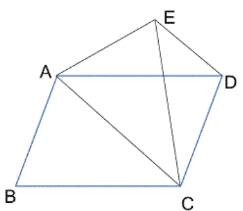
বিশেষ নির্বচনঃ ABCD একটি সামান্তরিক এবং ABCE একটি চতুর্ভুজ৷ AC কর্ণ ABCE চতুর্ভুজ আকারের ক্ষেত্রটিকে দুটি সমান অংশে বিভক্ত করে৷

প্রমাণ করতে হবে যে, AC || DE

প্রমানঃ ABCE চতুর্ভুজের AC কর্ণ চতুর্ভুজ আকারের ক্ষেত্রটিকে দুটি সমান অংশে বিভক্ত করে।

∴ ΔABC = ΔACE  ….(1)

ABCD সামান্তরিকের AC কর্ণ সামান্তরিককে দুটি সর্বসম ত্রিভুজে বিভক্ত করে।

∴ ΔABC = ΔACD  ….(2)

(1) নং ও (2) নং থেকে পাই,

ΔACE = ΔACD

ΔACE ও ΔACD এর ক্ষেত্রফল সমান এবং তারা একই ভূমি AC এর ওপর অবস্থিত।

∴ ΔACE ও ΔACD একই সমান্তরাল সরলরেখা যুগল AC ও ED এর মধ্যে অবস্থিত।

∴ AC || DE [প্রমানিত]

---

Q18. ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D; P এবং Q যথাক্রমে BC ও BA বাহুর উপর এমনভাবে অবস্থিত যে, ΔBPQ = ½ × ΔABC; প্রমাণ করি যে, DQ || PA

সমাধানঃ

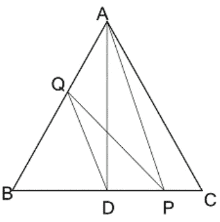
বিশেষ নির্বচনঃ ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D; P এবং Q যথাক্রমে BC ও BA বাহুর উপর এমনভাবে অবস্থিত যে, ΔBPQ = ½ × ΔABC; AD ও PQ পরস্পরকে O বিন্দুতে ছেদ করেছে।

প্রমাণ করতে হবে যে, DQ || PA

প্রমানঃ ΔABC এর AD মধ্যমা

ΔABD = ΔADC [∵ ত্রিভুজের মধ্যমা ত্রিভুজটিকে দুটি সমান ক্ষেত্রফলবিশিষ্ট ত্রিভুজে বিভক্ত করে।]

∴ ΔABD = ½ × ΔABC …..(1)

আবার ΔBPQ = ½ × ΔABC ….(2)

(1) নং ও (2) নং থেকে পাই-

ΔABD = ΔBPQ

বা, ΔBDQ + ΔDQA = ΔBDQ + ΔDQP

∴ ΔDQA = ΔDQP

ΔDQA ও ΔDQP একই ভূমি DQ এর ওপর অবস্থিত এবং এদের ক্ষেত্রফল সমান।

∴ ΔDQA ও ΔDQP একই সমান্তরাল সরলরেখাংশ যুগল DQ ও PA এর মধ্যে অবস্থিত।

∴ DQ || PA [প্রমানিত]

---

Q19. ABCD সামান্তরিকের AB, BC, CD এবং DA বাহুর মধ্যবিন্দু যথাক্রমে E, F, G ও H; প্রমাণ করি যে,

(i) EFGH একটি সামান্তরিক

(ii) EFGH সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফলের অর্ধেক৷

সমাধানঃ

বিশেষ নির্বচনঃ ABCD সামান্তরিকের AB, BC, CD এবং DA বাহুর মধ্যবিন্দু যথাক্রমে E, F, G ও H.

প্রমাণ করতে হবে যে,

(i) EFGH একটি সামান্তরিক

(ii) EFGH সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফলের অর্ধেক৷

অঙ্কনঃ B,D ও F,H যুক্ত করা হল।

প্রমানঃ ΔABD এর E, AB বাহুর মধ্যবিন্দু এবং H, AD বাহুর মধ্যবিন্দু।

∴ EH = ½ × BD এবং EH || BD  …..(1)

ΔCBD এর F, BC বাহুর মধ্যবিন্দু এবং G, CD বাহুর মধ্যবিন্দু৷

∴ FG = ½ × BD এবং FG || BD …..(2)

(1) নং ও (2) নং থেকে পাই

EH = FG এবং EH || FG

EFGH চতুর্ভুজের EH = FG এবং EH || FG

EFGH চতুর্ভুজটি একটি সামান্তরিক। [(i) নং প্রমানিত]

ABCD সামান্তরিকের BC = AD এবং BC || AD

BC ও DA বাহুর মধ্যবিন্দু যথাক্রমে F ও H

∴ BF = CF = ½ × BC;

AH = HD = ½ × AD

যেহেতু, BC = AD এবং BC || AD

∴ BF = AH = CF = DH এবং BF || AH, CF || DH

ABFH চতুর্ভুজের BF = AH এবং BF || AH

∴ ABFH একটি সামান্তরিক

CFHD চতুর্ভুজের CF = DH এবং CF || DH

∴ CFHD একটি সামান্তরিক

ΔEFH এবং সামান্তরিক ABFH একই ভূমি HF এবং একই সমান্তরাল সরলরেখাংশ যুগল HF এবং AB এর মধ্যে অবস্থিত।

∴ ΔEFH = ½ × ABFH সামান্তরিকের ক্ষেত্রফল

ΔGFH এবং সামান্তরিক CFHD একই ভূমি FH এবং একই সমান্তরাল সরলরেখাংশ যুগল FH এবং CD এর মধ্যে অবস্থিত।

∴ ΔGFH = ½ × CFHD সামান্তরিকের ক্ষেত্রফল

এখন, ΔEFH + ΔGFH

= ½ × ABFH সামান্তরিকের ক্ষেত্রফল + ½ × CFHD সামান্তরিকের ক্ষেত্রফল

= ½ × (ABFH সামান্তরিকের ক্ষেত্রফল + CFHD সামান্তরিকের ক্ষেত্রফল)

∴ EFGH সামান্তরিকের ক্ষেত্রফল = ½ × ABCD সামান্তরিকের [(ii) নং প্রমানিত]

---

Q20. ABCD ট্রাপিজিয়ামের AB || DC এবং BC বাহুর মধ্যবিন্দু E; প্রমাণ করি যে, AED ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল = ½ × ABCD ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল

সমাধানঃ

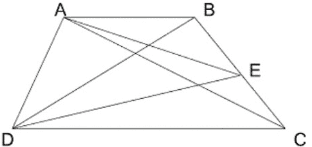
বিশেষ নির্বচনঃ ABCD ট্রাপিজিয়ামের AB || DC এবং BC বাহুর মধ্যবিন্দু E।

প্রমাণ করতে হবে যে, ΔAED = ½ × ABCD ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল

প্রমানঃ ΔABC এর AE মধ্যমা,

∴ 2ΔABE = ΔABC ….(1)

[∵ ত্রিভুজের মধ্যমা ত্রিভুজটিকে দুটি সমান ক্ষেত্রফলবিশিষ্ট ত্রিভুজে বিভক্ত করে]

ΔBDC এর DE মধ্যমা,

∴ 2ΔDEC = ΔBDC …..(2)

ΔBDC ও ΔADC একই ভূমি DC একই সমান্তরাল সরলরেখাংশ যুগল DC ও AB এর মধ্যে অবস্থিত।

∴ ΔBDC = ΔADC

বা, 2ΔDEC = ΔADC …..(3)

(1) + (3) করে পাই-

2ΔABE + 2ADEC = ΔABC + ΔADC

বা, 2 (ΔABE + ADEC ) = ABCD ট্রাপিজিয়ামের ক্ষেত্রফল

বা, 2 (ABCD ট্রাপিজিয়ামের ক্ষেত্রফল − ΔADE এর ক্ষেত্রফল) = ABCD ট্রাপিজিয়ামের ক্ষেত্রফল

বা, 2×ABCD ট্রাপিজিয়ামের ক্ষেত্রফল − 2×ΔADE এর ক্ষেত্রফল = ABCD ট্রাপিজিয়ামের ক্ষেত্রফল

বা, 2×ABCD ট্রাপিজিয়ামের ক্ষেত্রফল − ABCD ট্রাপিজিয়ামের ক্ষেত্রফল = 2×ΔADE এর ক্ষেত্রফল

বা, ABCD ট্রাপিজিয়ামের ক্ষেত্রফল = 2×ΔADE এর ক্ষেত্রফল

∴ ΔADE এর ক্ষেত্রফল = ½ × ABCD ট্রাপিজিয়ামের ক্ষেত্রফল [প্রমানিত]

---

Q21. বহু বিকল্পীয় প্রশ্ন (MCQ):

(i) ΔABC এর BC, CA এবং AB বাহুর মধ্যবিন্দু যথাক্রমে D, E ও F; যদি ΔABC = 16 বর্গসেমি. হয় তাহলে FBCE ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল-

(a) 40 বর্গসেমি.

(b) 8 বর্গসেমি.

(c) 12 বর্গসেমি

(d) 100 বর্গসেমি.

উত্তরঃ (c) 12 বর্গসেমি.

ABC ত্রিভুজের BE মধ্যমা

∴ ΔABE = ΔBEC = ½ × ΔABC

= ½ × 16 বর্গসেমি.

= 8 বর্গসেমি.

ABE ত্রিভুজের EF মধ্যমা

∴ ΔBFE = ½ × ΔABE

= ½ × 8 বর্গসেমি.

= 4 বর্গসেমি.

∴ FBCE ট্রাপিজিয়াম আকার ক্ষেত্রের ক্ষেত্রফল

= ΔBFE + ΔBEC

= (8 + 4) বর্গসেমি.

= 12 বর্গসেমি.

উত্তরঃ (c) 12 বর্গসেমি.

---

Q21. বহু বিকল্পীয় প্রশ্ন (MCQ):

(ii) A, B, C, D যথাক্রমে PQRS সামান্তরিকের PQ, QR, RS, SP বাহুর মধ্যবিন্দু। PQRS সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল 36 বর্গসেমি. হলে, ABCD ক্ষেত্রের ক্ষেত্রফল –

(a) 24 বর্গসেমি.

(b) 18 বর্গসেমি.

(c) 30 বর্গসেমি.

(d) 36 বর্গসেমি.

উত্তরঃ (b) 18 বর্গসেমি.

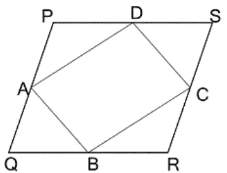
যেহেতু, A, B, C, D যথাক্রমে PQRS সামান্তরিকের PQ, QR, RS, SP বাহুর মধ্যবিন্দু।

∴ ABCD সামান্তরিকের ক্ষেত্রফল = ½ × PQRS সামান্তরিকের ক্ষেত্রফল

= ½ × 36 বর্গসেমি.

= 18 বর্গসেমি.

উত্তরঃ (b) 18 বর্গসেমি.

---

Q21. বহু বিকল্পীয় প্রশ্ন (MCQ):

(iii) ABCD সামান্তরিকের ভিতর O যে কোন একটি বিন্দু৷ ΔAOB + ΔCOD = 16 বর্গসেমি. হলে, ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল –

(a) 8 বর্গসেমি.

(b) 4 বর্গসেমি.

(c) 32 বর্গসেমি.

(d) 64 বর্গসেমি.

উত্তরঃ (c) 32 বর্গসেমি.

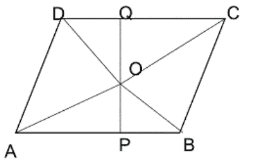
ABCD সামান্তরিকের AB = DC

ΔAOB + ΔCOD

= ½×AB×OP + ½×DC×OQ

= ½×AB×OP + ½×AB×OQ [∵ AB = DC]

= ½×AB×(OP + OQ)

= ½×AB×PQ

= ½ × ABCD সামান্তরিকের ক্ষেত্রফল

ABCD সামান্তরিকের ক্ষেত্রফল = 2 × (ΔAOB + ACOD)

= 2 × 16 বর্গসেমি.

= 32 বর্গসেমি.

উত্তরঃ (c) 32 বর্গসেমি.

---

Q21. বহু বিকল্পীয় প্রশ্ন (MCQ):

(iv) ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D, BD বাহুর মধ্যবিন্দু E এবং AE-এর মধ্যবিন্দু O; BOE ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল-

(a) ¹/₃ × ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল

(b) ¼ × ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল

(c) ¹/₆ × ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল

(d) ¹/₈ × ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল

উত্তরঃ (d) ¹/₈ × ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল

ABC ত্রিভুজের AD মধ্যমা

∴ ΔABD = ½ × ΔABC

ABD ত্রিভুজের AE মধ্যমা

∴ ΔABE = ½ × ΔABD

= ½ × ½ × ΔABC

= ¼ × ΔABC

∴ ΔABE = ¼ × ΔABC

ABE ত্রিভুজের BO মধ্যমা

∴ ΔBOE = ½ × ΔABE

= ½ × ¼ × ΔABC

= ¹/₈ × ΔABC

উত্তরঃ (d) ¹/₈ × ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল

---

Q21. বহু বিকল্পীয় প্রশ্ন (MCQ):

(v) একটি সামান্তরিক আকারের ক্ষেত্র, একটি আয়তক্ষেত্র এবং একটি ত্রিভুজাকার ক্ষেত্র একই ভূমি ও একই সমান্তরাল সরলরেখা যুগলের মধ্যে অবস্থিত এবং তাদের ক্ষেত্রফল যথাক্রমে P, R ও T হলে,

(a) P = R = 2T

(b) P = R = T/2

(c) 2P = 2R = T

(d) P = R = T

উত্তরঃ (a) P = R = 2T

একটি সামান্তরিক আকারের ক্ষেত্র, এবং একটি ত্রিভুজাকার ক্ষেত্র একই ভূমি ও একই সমান্তরাল সরলরেখা যুগলের মধ্যে অবস্থিত হলে, সামান্তরিক আকারের ক্ষেত্রফল = 2 × ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল 

∴ P = 2T ….(1)

একটি সামান্তরিক আকারের ক্ষেত্র, একটি আয়তক্ষেত্র যদি একই ভূমি ও একই সমান্তরাল সরলরেখা যুগলের মধ্যে অবস্থিত হয়, তাহলে সামান্তরিক আকারের ক্ষেত্রফল = আয়তক্ষেত্রের ক্ষেত্রফল [∵ আয়তক্ষেত্র এক ধরনের সামান্তরিক]

∴ P = R ….(2)

(1) নং ও (2) নং থেকে পাই

P = R = 2T

উত্তরঃ (a) P = R = 2T

---

Q22. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ

(i) ABCD সামান্তরিকের D বিন্দু থেকে AB বাহুর উপর লম্ব DE এবং B বিন্দু থেকে AD বাহুর উপর লম্ব BF; AB = 10 সেমি., AD = 8 সেমি. এবং DE = 6 সেমি. হলে, BF -এর দৈর্ঘ্য কত তা লিখি৷

সমাধানঃ

ABCD সামান্তরিকের AB = DC = 10 সেমি.

ABCD সামান্তরিকের ক্ষেত্রফল = ভূমি × উচ্চতা

= AB × DE

= 10 × 6 বর্গসেমি.

= 60 বর্গসেমি.

ধরি, BF = x সেমি.

আবার ABCD সামান্তরিকের ক্ষেত্রফল

= ভূমি × উচ্চতা

= DC × BF

= 10 × x বর্গসেমি.

∴ 10x = 60

x = 6

উত্তরঃ BF = 6 সেমি.

---

Q22. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ

(ii) ABCD সামান্তরিক আকার ক্ষেত্রের ক্ষেত্রফল 100 বর্গএকক; BC বাহুর মধ্যবিন্দু P; ABP ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল কত তা লিখি৷

সমাধানঃ

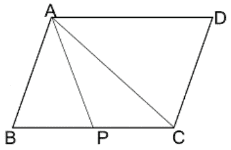
AC কর্ণ টানা হল।

আমরা জানি, সামান্তরিকের কর্ণ সামান্তরিককে দুটি সমান সর্বসম ত্রিভুজে বিভক্ত করে৷

∴ ΔABC = ΔADC

∴ ΔABC = ½ × ABCD সামান্তরিকের ক্ষেত্রফল

= ½ × 100 বর্গএকক

= 50 বর্গএকক

ΔABC এর AP মধ্যমা

∴ ΔABP = ½ × ΔABC

= ½ × 50 বর্গএকক

= 25 বর্গএকক

উত্তরঃ ABP ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল 25 বর্গএকক৷

---

Q22. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ

(iii) ABC ত্রিভুজের AD মধ্যমা এবং AC বাহুর উপর P এমন একটি বিন্দু যাতে ΔADP এর ক্ষেত্রফল : ΔABD এর ক্ষেত্রফল = 2 : 3 হয়। ΔPDC এর ক্ষেত্রফল : ΔABC এর ক্ষেত্রফল কত তা লিখি৷

সমাধানঃ

ΔADP এর ক্ষেত্রফল : ΔABD এর ক্ষেত্রফল = 2 : 3

ΔABD এর ক্ষেত্রফল = ³/₂ × ΔADP এর ক্ষেত্রফল …..(1)

ABC ত্রিভুজের AD মধ্যমা

∴ ΔABD = ΔACD = ½ × ΔABC ……(2)

∴ ΔACD = ³/₂ × ΔADP 

বা, ΔADP + ΔPDC = ³/₂ × ΔADP

বা, ³/₂ × ΔADP − ΔADP = ΔPDC

বা, ½ × ΔADP = ΔPDC

ΔPDC এর ক্ষেত্রফল : ΔABC এর ক্ষেত্রফল

= ½ × ΔADP : 2 × ΔABD [(2) নং এর সাহায্যে]

= ½ × ΔADP : 2 × ³/₂ × ΔADP [(1) নং এর সাহায্যে]

= ½ : 3

= 1 : 6

উত্তরঃ ΔPDC এর ক্ষেত্রফল : ΔABC এর ক্ষেত্রফল = 1 : 6

---

Q22. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ

(iv) ABDE একটি সামান্তরিক। F, ED বাহুর মধ্যবিন্দু৷ ABD ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল 20 বর্গসেমি. হলে, AEF ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল কত তা লিখি৷

সমাধানঃ

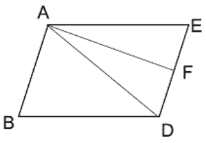
ABDE সামান্তরিকের AD কর্ণ

ΔABD = ΔADE 

∴ ΔADE = 20 বর্গসেমি.

আবার, ADE ত্রিভুজের AF মধ্যমা

∴ ΔAEF = ½ × ΔADE

= ½ × 20 বর্গসেমি.

= 10 বর্গসেমি.

উত্তরঃ AEF ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল 10 বর্গসেমি.

---

Q22. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ

(v) PQRS একটি সামান্তরিক। X এবং Y যথাক্রমে PQ এবং SR বাহুর মধ্যবিন্দু। কর্ণ SQ যুক্ত করি। সামান্তরিক XQRY আকার ক্ষেত্রের ক্ষেত্রফল : QSR ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল কত তা লিখি৷

সমাধানঃ

PQRS সামান্তরিকের QS কর্ণ

∴ PQRS সামান্তরিকের ক্ষেত্রফল = 2 × ΔQSR

আবার, X, Y যথাক্রমে PQ ও SR বাহুর মধ্যবিন্দু

∴ XQRY সামান্তরিকের ক্ষেত্রফল

= ½ × PQRS সামান্তরিকের ক্ষেত্রফল

= ½ × 2 × ΔQSR

= ΔQSR এর ক্ষেত্রফল

উত্তরঃ XQRY সামান্তরিকের ক্ষেত্রফল : ΔQSR এর ক্ষেত্রফল = 1 : 1

---

 

Koshe Dekhi 12 Class 9

Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9.

Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9.

Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9.

Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9.

Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9, Koshe Dekhi 12 Class 9.

আরও দেখো :

গণিত প্রকাশ নবম শ্রেণি সমাধান

গণিত প্রকাশ দশম শ্রেণি সমাধান 

গণিত প্রভা সপ্তম শ্রেণি সমাধান 

গণিত প্রভা ষষ্ট শ্রেণি সমাধান