নীচের প্রশ্নগুলির উত্তর লেখ :
1. বহুমুখী উত্তরধর্মী প্রশ্ন (MCQs)
(i) বাস্তব সহগযুক্ত একচলবিশিষ্ট দ্বিঘাত সমীকরণটি হল
(a)
(b)
(c)
(d)
সমাধানঃ
বা,
বা, ……(i)
যেহেতু, (i) নং সমীকরণটিকে [ যেখানে, a ≠ 0 এবং a, b, c বাস্তব সংখ্যা ] আকারে লেখা যায়, তাই
সমীকরণটি হল বাস্তব সহগযুক্ত একচলবিশিষ্ট দ্বিঘাত সমীকরণ।
উত্তরঃ (c)
(ii) সমীকরণটির বীজ দুটি হল
(a) −1, −3
(b) −1, 3
(c) 1, −3
(d) 1, 3
সমাধানঃ
আমরা জানি,
দুই বা ততোধিক রাশির গুনফল শূন্য হলে তারা পৃথক পৃথকভাবে শূন্য হয়।
অর্থাৎ,
(2x − 2) = 0
বা, 2x = 2
বা,
∴ x = 1
অথবা,
(x + 3) = 0
∴ x = − 3
উত্তরঃ (c)
(iii) বার্ষিক 10% সরল সুদের হারে 50 টাকার 2 বছরের সুদ ঐ একই হারে 100 টাকার 1 বছরের সুদের
(a) দ্বিগুণ
(b) অর্ধেক
(c) এক চতুর্থাংশ
(d) সমান
সমাধানঃ
প্রথমক্ষেত্রে :
আসল (p) = 50 টাকা,
সময় (t) = 2 বছর,
সুদের হার (r) = 10%
আমরা জানি,
মোট সুদ
বা,
∴ I = 10
দ্বিতীয়ক্ষেত্রে :
আসল (p) = 100 টাকা,
সময় (t) = 1 বছর,
সুদের হার (r) = 10%
আমরা জানি,
মোট সুদ
বা,
∴ I = 10
উত্তরঃ (d)
(iv) O কেন্দ্রীয় বৃত্তের PQ ও RS দুটি সমান দৈর্ঘ্যের জ্যা। O বিন্দু থেকে PQ জ্যা -এর দূরত্ব 8 সেমি হলে, O বিন্দু থেকে RS জ্যা এর দূরত্ব কত হবে ?
(a) 8 সেমি.
(b) 16 সেমি.
(c) 4 সেমি.
(d) 10 সেমি.
সমাধানঃ
একটি বৃত্তের দুটি জ্যা -এর দৈর্ঘ্য তখনই সমান হবে যখন জ্যা দুটি কেন্দ্র থেকে সমদূরত্বে ও কেন্দ্রের বিপরীত পাশে অবস্থান করবে।
সুতরাং,
O বিন্দু থেকে RS জ্যা এর দূরত্ব 8 সেমি.।
উত্তরঃ (a)
2. সত্য/মিথ্যা লেখো (T/F) :
(i) একটি ঘনকের প্রতিটি ধারের দৈর্ঘ্য অর্ধেক করা হলে, ঘনকটির আয়তন প্রথম ঘনকের অংশ হবে।
সমাধানঃ
ধরি, প্রথমে ঘনকটির প্রতিটি ধারের দৈর্ঘ্য ছিল a একক।
∴ ঘনকটির আয়তন ছিল ঘনএকক।
এখন ঘনকের প্রতিটি ধারের দৈর্ঘ্য অর্ধেক করা হলে,
বর্তমানে ঘনকের প্রতিটি ধারের দৈর্ঘ্য একক
∴ বর্তমানে ঘনকটির আয়তন
ঘনএকক
ঘনএকক
= প্রথম ঘনকের আয়তন ×
= প্রথম ঘনকের অংশ
উত্তরঃ বিবৃতিটি সত্য
(ii) হলে, a : b : c = 4 : 3 : 2 হবে।
সমাধানঃ
ধরি,
অর্থাৎ, a = 2k, b = 3k, c = 4k
∴ a : b : c
= 2k : 3k : 4k
= 2 : 3 : 4
উত্তরঃ বিবৃতিটি মিথ্যা
(iii) আসল P টাকা এবং বার্ষিক চক্রবৃদ্ধি সুদের হার r% হলে, দ্বিতীয় বছরের মূলধন টাকা।
সমাধানঃ
আসল = P টাকা,
সময় (t) = 1 বছর,
চক্রবৃদ্ধি সুদের হার = r %
আমরা জানি,
চক্রবৃদ্ধি সুদের ক্ষেত্রে
সবৃদ্ধিমূল ( অর্থাৎ, সুদ + আসল) =
বা,
আমরা জানি, চক্রবৃদ্ধি সুদের ক্ষেত্রে প্রথম বছরের সবৃদ্ধিমূল, দ্বিতীয় বছরের ক্ষেত্রে আসল (মূলধন) হয়।
সুতরাং, দ্বিতীয় বছরের ক্ষেত্রে মূলধন হবে টাকা।
উত্তরঃ বিবৃতিটি মিথ্যা
(iv) চিত্রে O কেন্দ্রবিশিষ্ট বৃত্তে AB একটি ব্যাস।বৃত্তের ভিতরে Q একটি বিন্দু। ∠AQB সর্বদা সূক্ষকোণ হবে।
Note : প্রশ্নটি ভুল আছে। সঠিক প্রশ্নটি নিচে দেওয়া হলো –
চিত্রে O কেন্দ্রবিশিষ্ট বৃত্তে AB একটি ব্যাস।বৃত্তের ভিতরে Q একটি বিন্দু। ∠AQB সর্বদা স্থূলকোণ হবে।
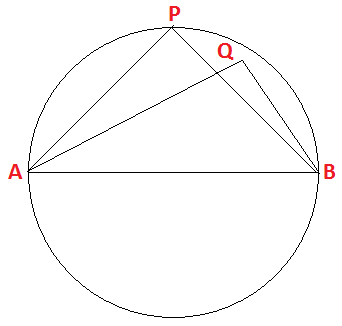
সমাধানঃ
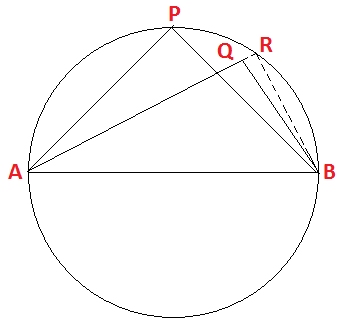
প্রমাণ করতে হবে যে, ∠AQB সর্বদা স্থূলকোণ হবে।
অঙ্কন : AQ কে বর্ধিত করা হলো যা বৃত্তকে R বিন্দুতে ছেদ করেছে। B, R যুক্ত করা হলো।
প্রমাণ : ∵ AB হলো ব্যাস এবং R হলো বৃত্তের উপর অবস্থিত যে কোনো একটি বিন্দু।
∴ ∠ARB হলো অর্ধবৃত্তস্থ কোণ অর্থ্যাৎ, ∠ARB = 90°
এখন, যেহেতু ΔRBQ -এর ∠AQB হলো বহিঃকোণ এবং ∠QRB ও ∠RQB হলো অন্তঃস্থ বিপরীত কোনসমূহ।
∴ ∠AQB = ∠QRB + ∠RQB
বা, ∠AQB = ∠ARB + ∠RQB [∠QRB ও ∠ARB হলো একই কোণ]
বা, ∠AQB = 90° + ∠RQB [∠ARB = 90°]
অর্থ্যাৎ, ∠AQB > 90°
এবং ∠AQB < 180° [∴ ∠AQB হলো ΔAQB -এর একটি কোণ এবং ত্রিভুজের তিনটি কোণের মধ্যে কোনো কোণের মান 180° অপেক্ষা বৃহত্তর হতে পারেনা।]
সুতরাং, ∠AQB হলো সর্বদা স্থূলকোণ। (প্রমাণিত)
3. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A) :
(i) একটি লম্ববৃত্তাকার চোঙের আয়তন এবং বক্রতলের ক্ষেত্রফল সংখ্যামানে সমান হলে, উহার ব্যাসার্ধ নির্ণয় কর।
সমাধানঃ
আমরা জানি,
লম্ববৃত্তাকার চোঙের আয়তন
ঘন একক
এবং বক্রতলের ক্ষেত্রফল
বর্গ একক [যেখানে, r = ব্যাসার্ধ ও h = উচ্চতা ]
প্রশ্নানুসারে,
∴ r = 2
উত্তরঃ নির্ণেয় লম্ববৃত্তাকার চোঙের ব্যাসার্ধ 2 একক।
(ii) দেখাও যে মিশ্র দ্বিঘাত করণী -এর অনুবন্ধী করণী হল
সমাধানঃ
যা একটি মূলদ সংখ্যা
আবার,
যা একটি মূলদ সংখ্যা
এখন, যেহেতু ও
-এর গুনফল ও যোগফল উভয়ই মূলদ সংখ্যা, তাই
-এর অনুবন্ধী করণী
4. যুক্তি দিয়ে প্রমাণ করো যে, বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক।
সমাধানঃ
প্রদত্ত: ধরা যাক, ABCD হলো একটি বৃত্তস্থ চতুর্ভুজ এবং O হলো বৃত্তের কেন্দ্র।
প্রামাণ্য বিষয়ঃ
(i) ∠ABC+∠ADC = 180°
(ii) ∠BAC + ∠BCD = 180°
অঙ্কনঃ A , O এবং C , O যুক্ত করা হলো।
প্রমাণঃ ABC বৃত্তচাপের উপর অবস্থিত কেন্দ্রস্থ কোণ ∠AOC এবং বৃত্তস্থ কোণ ∠ADC
∴ ∠AOC = 2∠ADC ……. (i)
[একই বৃত্তচাপের উপর অবস্থিত কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন হয়]
আবার, ADC বৃত্তচাপের উপর অবস্থিত কেন্দ্রস্থ প্রবৃদ্ধ কোণ ∠AOC এবং বৃত্তস্থ কোণ ∠ABC
∴ প্রবৃদ্ধ ∠AOC = 2∠ABC ……. (ii)
[একই বৃত্তচাপের উপর অবস্থিত কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন হয়]
এখন, [(i) + (ii)] করে পাই ,
2∠ADC + 2∠ABC = ∠AOC + প্রবৃদ্ধ ∠AOC
বা, 2(∠ADC + ∠ABC) = 360°
বা, ∠ADC + ∠ABC =
∴ ∠ADC + ∠ABC = 180° (প্রমাণিত)
আবার,
ABCD চতুর্ভুজের চারটি কোণের সমষ্টি 360°
∴ ∠BAC + ∠ABC + ∠BCD + ∠ADC = 360°
বা, (∠ADC + ∠ABC) + (∠BAC + ∠BCD) = 360°
বা, 180° + (∠BAC + ∠BCD) = 360°
বা, ∠BAC + ∠BCD = 360° − 180°
∴ ∠BAC + ∠BCD = 180° (প্রমাণিত)