Koshe Dekhi 17 Class 9

Q1. ABC ত্রিভুজে ∠B ও ∠C -এর অন্তর্সমদ্বিখন্ডক I বিন্দুতে ছেদ করেছে। প্রমান করি ${\color{Blue} \angle BIC=90^{\circ}+\frac{\angle BAC}{2}}$

বিশেষ নির্বচনঃ ABC ত্রিভুজে ∠B ও ∠C -এর অন্তসমদ্বিখন্ডক I বিন্দুতে ছেদ করেছে।

প্রমান করতে হবে যে, $\angle BIC=90^{\circ}+\frac{\angle BAC}{2}$

প্রমাণঃ BI, ∠B এর অন্তসমদ্বিখন্ডক
∴ ∠ABC = 2∠IBC ….(1)

CI, ∠C এর অন্তসমদ্বিখন্ডক
∴∠ACB = 2∠ACI ….(2)

ΔABC এর ∠ABC +∠ACB + ∠BAC = 180°
বা, 2∠IBC + 2∠ACI + ∠BAC = 180°
বা, 2(∠IBC + ∠ACI) = 180° − ∠BAC
বা, ∠IBC + ∠ACI = 90° − ^∠BAC/₂ ….(3)

ΔIBC এর ∠IBC + ∠ICB + ∠BIC = 180°
বা, 90° − ^∠BAC/₂+ ∠BIC = 180° [(3)নং থেকে পাই]
বা, ∠BIC = 180° − 90° + ^∠BAC/₂
∴ ∠BIC = 90° + ^∠BAC/₂[প্রমানিত]

Q2. একটি ত্রিভুজের তিনটি মধ্যমার দৈর্ঘ্য সমান হলে প্রমান করি যে, ত্রিভুজটি সমবাহু।

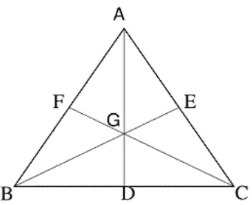
Koshe Dekhi 17 Class 9

বিশেষ নির্বচনঃ ABC একটি ত্রিভুজ যার মধ্যমা তিনটি সমান অর্থাৎ AD = BE = CF; মধ্যমা তিনটি G বিন্দুতে ছেদ করেছে।

প্রমাণ করতে হবে যে, ABC একটি সমবাহু ত্রিভুজ।

প্রমাণঃ G, ABC ত্রিভুজের ভারকেন্দ্র।
আমরা জানি, ত্রিভুজের ভারকেন্দ্র মধ্যমাকে 2 : 1 অনুপাতে অন্তর্বিভক্ত করে।
∴ AG = ²/₃ AD, BG = ²/₃BE, CG = ²/₃CF
এবং DG = ¹/₃AD, EG = ¹/₃BE, FG = ¹/₃CF
আবার, AD = BE = CF
∴ AG = BG = CG ….(1)
এবং DG = EG = FG ….(2)

ΔFGB এবং ΔEGC এর –
BG = CG [(1) নং থেকে পাই]
∠FGB = বিপ্রতীপ ∠EGC
FG = EG [(2) নং থেকে পাই]
∴ ΔFGB ≅ ΔEGC [সর্বসমতার S-A-S শর্তানুসারে]
BF = CE [সর্বসম ত্রিভুজের অনুরূপ বাহু]
বা, 2BF = 2CE
∴ AB = AC …..(3)

আবার, ΔCGD এবং ΔAGF এর –
CG = AG [(1) নং থেকে পাই]
∠CGD = বিপ্রতীপ ∠AGF
DG = FG [(2) নং থেকে পাই]
∴ ΔCGD ≅ ΔAGF [সর্বসমতার S-A-S শর্তানুসারে]
CD = AF [সর্বসম ত্রিভুজের অনুরূপ বাহু]
বা, 2CD = 2AF
∴ BC = AB ….(4)

(3) নং ও (4) নং থেকে পাই,
AB = BC = CA
∴ ΔABC একটি সমবাহু ত্রিভুজ [প্রমানিত]

Q3. প্রমান করি যে, সমবাহু ত্রিভুজের পরিকেন্দ্র, অন্তঃকেন্দ্র, ভরকেন্দ্র ও লম্ববিন্দু সমাপতিত হয়।

Koshe Dekhi 17 Class 9

বিশেষ নির্বচনঃ ABC ত্রিভুজের AD, BE, CF মধ্যমা তিনটি G বিন্দুতে মিলিত হয়েছে।

প্রমাণ করতে হবে যে, ত্রিভুজের পরিকেন্দ্র, অন্তঃকেন্দ্র, ভরকেন্দ্র ও লম্ববিন্দু সমাপতিত হয়।

প্রমাণঃ ABC ত্রিভুজের AD, BE, CF মধ্যমা তিনটি G বিন্দুতে মিলিত হয়েছে।
∴ ABC ত্রিভুজের ভারকেন্দ্র G.
আমরা জানি সমবাহু ত্রিভুজের উচ্চতাই হল মধ্যমা।
∴ ABC ত্রিভুজের লম্ববিন্দু G

আমরা জানি, ত্রিভুজের ভারকেন্দ্র মধ্যমাকে 2 : 1 অনুপাতে অন্তর্বিভক্ত করে।
∴ AG = ²/₃ AD, BG = ²/₃BE, CG = ²/₃CF
এবং DG = ¹/₃AD, EG = ¹/₃BE, FG = ¹/₃CF
যেহেতু, সমবাহু ত্রিভুজের ক্ষেত্রে প্রত্যেকটি মধ্যমা সমান।
∴ DG = EG = CF এবং AG = BG = CG
আবার, AD⊥BC, BE⊥CA ও CF⊥AB
∴ DG⊥BC, EG⊥CA ও CG⊥AB
∴ G বিন্দু থেকে প্রত্যেকটি বাহুর লম্ব দূরত্ব সমান।
সুতরাং, ABC ত্রিভুজের অন্তকেন্দ্র G.

যেহেতু, AG = BG = CG
∴ G বিন্দু থেকে ABC ত্রিভুজের শীর্ষবিন্দুগুলির দুরত্ব সমান।
সুতরাং, ABC ত্রিভুজের পরিকেন্দ্র G.

∴ ABC ত্রিভুজের ভারকেন্দ্র, লম্ববিন্দু, অন্তকেন্দ্র ও পরিকেন্দ্র হল G
∴ সমবাহু ত্রিভুজের পরিকেন্দ্র, অন্তঃকেন্দ্র, ভরকেন্দ্র ও লম্ববিন্দু সমাপতিত হয়। [প্রমানিত ]

Q4. ABC ত্রিভুজের AD, BE ও CF মধ্যমা। প্রমান করি যে, ABC ও DEF ত্রিভুজের ভরকেন্দ্র একই বিন্দু।

Koshe Dekhi 17 Class 9

বিশেষ নির্বচনঃ ধরি, ABC ত্রিভুজের AD, BE ও CF মধ্যমা তিনটি পরস্পরকে G বিন্দুতে ছেদ করেছে।
∴ ABC ত্রিভুজের ভারকেন্দ্র G.

প্রমাণ করতে হবে যে, ABC ও DEF ত্রিভুজের ভরকেন্দ্র একই বিন্দু৷ অর্থাৎ, DEF ত্রিভুজের ভারকেন্দ্র G প্রমাণ করলেই প্রমানিত হবে ABC ও DEF ত্রিভুজের ভরকেন্দ্র একই বিন্দু৷

প্রমাণঃ ΔABC এর AB ও AC বাহুর মধ্যবিন্দু যথাক্রমে F ও E.
∴ FE || BC এবং FE = ½ BC
D, BC বাহুর মধ্যবিন্দু
∴ BD = DC = ½ BC
∴ FE = BD
এখন BDEF চতুর্ভুজের FE || BD [∵ FE || BC]
এবং FE = BD
∴ BDEF চতুর্ভুজটি একটি সামান্তরিক।

অনুরূপভাবে আমরা প্রমাণ করতে পারি যে, DCEF এবং DEAF উভয়েই সামান্তরিক।

আমরা জানি, সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে।
∴ BDEF সামান্তরিক থেকে পাই, FY = YD
∴ Y, FD বাহুর মধ্যবিন্দু
DCEF সামান্তরিক থেকে পাই, DZ = ZE
∴ Z, DE বাহুর মধ্যবিন্দু
এবং DEAF সামান্তরিক থেকে পাই, FX = XE
∴ X, FE বাহুর মধ্যবিন্দু

DEF ত্রিভুজের DE, EF ও FD বাহুর মধ্যবিন্দু যথাক্রমে Z, X ও Y.
∴ DEF ত্রিভুজের মধ্যমা তিনটি হল DE, EF ও FD.

DE, EF ও FD মধ্যমা তিনটি G বিন্দুতে ছেদ করেছে।
∴ DEF ত্রিভুজের ভারকেন্দ্র G.
∴ ABC ও DEF ত্রিভুজের ভরকেন্দ্র একই বিন্দু৷[প্রমানিত ]

Q5. প্রমান করি যে, একটি ত্রিভুজের দুটি মধ্যমার দৈর্ঘ্যের সমষ্টি তৃতীয় মধ্যমার দৈর্ঘ্য অপেক্ষা বৃহত্তর।

Koshe Dekhi 17 Class 9

বিশেষ নির্বচনঃ ধরি, ABC ত্রিভুজের AD, BE ও CF মধ্যমা তিনটি পরস্পরকে G বিন্দুতে ছেদ করেছে।

প্রমাণ করতে হবে যে, একটি ত্রিভুজের দুটি মধ্যমার দৈর্ঘ্যের সমষ্টি তৃতীয় মধ্যমার দৈর্ঘ্য অপেক্ষা বৃহত্তর।

অঙ্কনঃ AD কে H পর্যন্ত এমনভাবে বর্ধিত করা হল যে AG = GH হয়। B, H ও C, H যুক্ত করা হল।

প্রমাণঃ ΔABH থেকে পাই,
F, AB বাহুর মধ্যবিন্দু এবং G, AH বাহুর মধ্যবিন্দু
∴ FG || BH
∴GC || BH ….(1)

একইরকমভাবে ΔACH থেকে পাই,
BG || HC …..(2)

BGCH চতুর্ভুজের GC || BH এবং BG|| HC
∴ BGCH চতুর্ভুজটি একটি সামন্তরিক।
∴ BH = CG ….(3) [সামান্তরিকের বিপরীত বাহু দুটি সমান]

ΔBGH থেকে পাই,
BG + GH > BH [∵ ত্রিভুজের দুটি বাহুর সমষ্টি তৃতীয় বাহু অপেক্ষা বৃহত্তর]
বা, BG + AG > CG [(3) নং থেকে পাই]
বা, ³/₂ BG + ³/₂AG > ³/₂CG
∴ BE + AD > CF
[::ভারকেন্দ্র মধ্যমাকে 2 : 1 অনুপাতে বিভক্ত করে। ∴ BE = ³/₂ BG, AD = ³/₂ AG ও CF = ³/₂ CG]

একইরকমভাবে, BE + CF > AD এবং AD + CF > BE
∴ ত্রিভুজের দুটি মধ্যমার দৈর্ঘ্যের সমষ্টি তৃতীয় মধ্যমার দৈর্ঘ্য অপেক্ষা বৃহত্তর। [প্রমানিত]

Q6. ABC ত্রিভুজের AD, BE ও CF মধ্যমা। প্রমান করি যে,
(i) 4(AD + BE + CF) > 3(AB + BC + CA)
(ii) 3(AB + BC + CA) > 2(AD + BE + CF)

Koshe Dekhi 17 Class 9

বিশেষ নির্বচনঃ ধরি, ABC ত্রিভুজের AD, BE ও CF মধ্যমা তিনটি G বিন্দুতে ছেদ করেছে।

প্রমাণ করতে হবে যে,
(i) 4(AD + BE + CF) > 3(AB + BC + CA)
(ii) 3(AB + BC + CA) > 2(AD + BE + CF)

প্রমাণঃ (i) আমরা জানি, ত্রিভুজের ভারকেন্দ্র, মধ্যমাকে 2 : 1 অনুপাতে বিভক্ত করে।
²/₃ BE = BG এবং ²/₃ CF = CG
ΔBGC থেকে পাই,
BG + GC > BC
বা, ²/₃ BE + ²/₃ CF > BC
∴ 2BE + 2CF > 3BC …..(1)

একইরকমভাবে, ΔAGC থেকে পাই,
2AD + 2CF > 3AC …..(2)
এবং ΔAGB থেকে পাই,
2AD + 2BE > 3AB …..(3)

(1) + (2) + (3) করে পাই
2BE + 2CF + 2AD + 2CF + 2AD + 2BE >3BC + 3AC + 3AB
⇒ 4AD + 4BE + 4CF > 3(AB + BC + CA)
∴ 4(AD+BE+CF) > 3 (AB+BC+CA) [(i) প্রমানিত]

(ii) ΔACD থেকে পাই,
CA + CD > AD
বা, CA + ^BC/₂> AD …..(4) [∵ AD হল মধ্যমা, ∴ BD = CD = ^BC/₂]

একইরকমভাবে,
ΔACD থেকে পাই,
AB + ^CA/₂ > BE ….(5)

এবং ΔBFC থেকে পাই,
BC + ^AB/₂ > CF ….(6)

(4) + (5) + (6) করে পাই.
CA + ^BC/₂+ AB + ^CA/₂+ BC + ^AB/₂ > AD + BE + CF
⇒ ³/₂ AB + ³/₂ BC + ³/₂ CA > AD + BE + CF
3(AB + BC + CA) > 2(AD + BE + CF) [(ii) প্রমানিত]

Q7. ΔABC –এর AD, BE ও CF মধ্যমা তিনটি G বিন্দুতে পরস্পরকে ছেদ করেছে। ΔABC এর ক্ষেত্রফল 36 বর্গসেমি. হলে, (i) ΔAGB এর ক্ষেত্রফল (ii) ΔCGE এর ক্ষেত্রফল (iii) চতুৰ্ভুজ BDGF -এর ক্ষেত্রফল নির্ণয় করি।

সমাধানঃ

Koshe Dekhi 17 Class 9

(i) ΔABC এর AD, BE ও CF মধ্যমা তিনটি G বিন্দুতে পরস্পরকে ছেদ করেছে।
∴ ΔAGB = ΔBGC = ΔAGC = ¹/₃ × ΔABC
∴ ΔAGB এর ক্ষেত্রফল = ¹/₃ × ΔABC এর ক্ষেত্রফল = ¹/₃× 36 বর্গসেমি.
উত্তরঃ ΔAGB এর ক্ষেত্রফল = 12 বর্গসেমি.

(ii) ΔAGC এর AE = EC [∵ E, AC বাহুর মধ্যবিন্দু]
∴ GE, ΔAGC এর মধ্যমা
সুতরাং, ΔCGE = ΔAGE = ¹/₂ × ΔAGC
বা, ΔCGE = ¹/₂ × ΔAGC
বা, ΔCGE = ¹/₂ × ¹/₃ × ΔABC এর ক্ষেত্রফল
বা, ΔCGE এর ক্ষেত্রফল = ¹/₆ × 36 বর্গসেমি.
উত্তরঃ ΔCGE এর ক্ষেত্রফল = 6 বর্গসেমি.

(iii) চতুর্ভুজ BDGF = ΔABD − ΔAFG
= ¹/₂ ΔABC − ¹/₂ ΔAGB
= ¹/₂× ΔABC − ¹/₂ × ¹/₃× ΔABC
= (¹/₂ × 36 − ¹/₂ × ¹/₃× 36) বর্গসেমি.
= (18 − 6 ) বর্গসেমি. = 12 বর্গসেমি.
উত্তরঃ চতুর্ভুজ BDGF – এর ক্ষেত্রফল 12 বর্গসেমি.

Q8. ABC ত্রিভুজের AD, BE ও CF মধ্যমা। যদি ²/₃AD = BC হয়, তাহলে প্রমান করি যে, অপর দুটি মধ্যমার অন্তর্ভুক্ত কোণের পরিমাপ 90°.

Koshe Dekhi 17 Class 9

বিশেষ নির্বচনঃ ধরি, ABC ত্রিভুজের AD, BE ও CF মধ্যমা তিনটি G বিন্দুতে ছেদ করেছে।

প্রমাণ করতে হবে যে, BE ও CF বাহুদ্বয়ের অন্তর্ভুক্ত কোণ 90°

প্রমাণঃ যেহেতু, G, ΔABC এর ভারকেন্দ্র
∴ AD = 3DG
আবার, ²/₃AD = BC
বা, AD = ³/₂ BC
বা, 3DG = ³/₂BC
∴ DG = ½ BC
এখন BD = DC = ½ BC [∵ D, BC বাহুর মধ্যবিন্দু]
∴ BD = DC = DG

ΔBDG এর BD = DG
∴ ∠GBD =∠BGD .….(1)

ΔCDG এর CD = DG
∴ ∠GCD =∠CGD …..(2)

যেহেতু, ত্রিভুজের তিনটি কোণের সমষ্টি 180°
ΔBDG থেকে পাই, ∠GBD + ∠BGD + ∠BDG = 180° …..(3)
এবং ΔCDG থেকে পাই, ∠GCD + ∠CGD + ∠CDG = 180° …..(4)

(3) নং ও (4) নং যোগ করে পাই,
∠GBD + ∠BGD + ∠BDG + ∠GCD + ∠CGD + ∠CDG = 180° + 180°
বা, ∠BGD + ∠BGD + ∠BDG + ∠CGD + ∠CGD + ∠CDG = 360° [(1) ও (2) এর সাহায্যে]
বা, 2∠BGD + ∠BDG + 2∠CGD + ∠CDG = 360°
বা, 2(∠BGD + ∠CGD) + (∠BDG + ∠CDG) = 360°
বা, 2(∠BGD + ∠CGD) + 180° = 360°
বা, 2(∠BGD + ∠CGD) = 360° − 180°
বা, 2∠BGC = 180°
∴ ∠BGC = 90°
∴ BE ও CF বাহুদ্বয়ের অন্তর্ভুক্ত কোণ 90°. [প্রমানিত]

Q9. ABCD সামান্তরিকের BC এবং CD বাহুর মধ্যবিন্দু যথাক্রমে P এবং Q; AP এবং AQ কর্ণ BD-কে যথাক্রমে K ও L বিন্দুতে ছেদ করে। প্রমান করি যে, BK = KL = LD

Koshe Dekhi 17 Class 9

বিশেষ নির্বচনঃ ABCD সামান্তরিকের BC এবং CD বাহুর মধ্যবিন্দু যথাক্রমে P এবং Q; AP এবং AQ কর্ণ BD-কে যথাক্রমে K ও L বিন্দুতে ছেদ করে।

প্রমান করতে হবে যে, BK = KL = LD

অঙ্কনঃ CK || QL এবং PK || CL অঙ্কন করা হল।

প্রমাণঃ ΔCKD এর Q, CD বাহুর মধ্যবিন্দু এবং CK || QL
L, KD বাহুর মধ্যবিন্দু
∴ KL = LD …..(1)
ΔBCL এর P, BC বাহুর মধ্যবিন্দু এবং PK || CL
∴ K, BL বাহুর মধ্যবিন্দু
∴ BK = KL …..(2)
(1) নং ও ( 2 ) নং থেকে পাই,
BK = KL = LD [প্রমানিত]

Q10. বহুবিকল্পীয় প্রশ্ন (M.C.Q.):

(i) ABC ত্রিভুজের পরিকেন্দ্র O; ∠BOC = 80° হলে, ∠BAC এর পরিমাপ-
(a) 40°
(b) 160°
(c) 130°
(d) 110°

উত্তরঃ (a) 40°

Koshe Dekhi 17 Class 9

ABC ত্রিভুজের পরিকেন্দ্র হলো O.
∠BOC = 2∠BAC
∴ ∠BAC = ½ × ∠BOC
= ½ × 80°
= 40°

উত্তরঃ (a) 40°

Q10. বহুবিকল্পীয় প্রশ্ন (M.C.Q.):

(ii) ABC ত্রিভুজের লম্ববিন্দু O; ∠BAC = 40° হলে, ∠BOC-এর পরিমাপ
(a) 80°
(b) 140°
(c) 110°
(d) 40°

উত্তরঃ (b) 140°

Koshe Dekhi 17 Class 9

AFOE চতুর্ভুজের ∠OFA = 90° এবং ∠OEA = 90°
∠EAF = ∠BAC = 40°

AFOE চতুর্ভুজ থেকে পাই,
∠EOF = 360° − ∠OFA − ∠OEA − ∠EAF
= 360° − 90° − 90° − 40° = 140°

∠BOC = বিপ্রতীপ ∠EOF
= 140°

উত্তরঃ (b) 140°

Q10. বহুবিকল্পীয় প্রশ্ন (M.C.Q.):

(iii) ABC ত্রিভুজের অন্তঃকেন্দ্র O; ∠BAC=40° হলে, ∠BOC-এর পরিমাপ
(a) 80°
(b) 110°
(c) 140°
(d) 40°

উত্তরঃ (b) 110°

Koshe Dekhi 17 Class 9

ΔABC তে
∠ABC + ∠ACB + ∠BAC = 180°
⇒ 2∠OBC + 2∠OCB + 40° = 180°
⇒ 2(∠OBC + ∠OCB) = 180°− 40°
∴ ∠OBC + ∠OCB = 70°

ΔOBC তে
∠OBC + ∠OCB + ∠BOC = 180°
⇒ 70° + ∠BOC = 180°
⇒ ∠BOC = 180° − 70°
∴ ∠BOC = 110°

উত্তরঃ (b) 110°

Q10. বহুবিকল্পীয় প্রশ্ন (M.C.Q.):

(iv) ABC ত্রিভুজের ভরকেন্দ্র G; GBC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল 12 বর্গসেমি. হলে, ABC ত্রিভুজাকার ক্ষেত্রের ক্ষেত্রফল –
(a) 24 বর্গসেমি.
(b) 6 বর্গসেমি.
(c) 36 বর্গসেমি.
(d) কোনোটিই নয়

উত্তরঃ (c) 36 বর্গসেমি.

Koshe Dekhi 17 Class 9

আমরা জানি, ABC ত্রিভুজের AD, BE ও CF মধ্যমা G (ভারকেন্দ্র) বিন্দুতে ছেদ করলে
ΔABC ত্রিভুজের ক্ষেত্রফল = 3 × ΔBGC ত্রিভুজের ক্ষেত্রফল
= 3 × 12 বর্গসেমি.
= 36 বর্গসেমি.

উত্তরঃ (c) 36 বর্গসেমি.

Q10. বহুবিকল্পীয় প্রশ্ন (M.C.Q.):

(v) ABC সমকোণী ত্রিভুজের পরিব্যাসার্ধের দৈর্ঘ্য 5 সেমি. হলে, অতিভুজের দৈর্ঘ্য –
(a) 2.5 সেমি.
(b) 10সেমি.
(c) 5 সেমি
(d) কোনোটিই নয়৷

উত্তরঃ (b) 10 সেমি.

আমরা জানি, সমকোণী ত্রিভুজের পরিব্যাসার্ধের দৈর্ঘ্য অতিভুজের দৈর্ঘ্যের অর্ধেক৷
∴ সমকোণী ত্রিভুজের অতিভুজের দৈর্ঘ্য
= 2 × 5 সেমি.
= 10 সেমি.

উত্তরঃ (b) 10 সেমি.

Q11. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ

(i) একটি ত্রিভুজের বাহুর দৈর্ঘ্য 6 সেমি., 8 সেমি. ও 10 সেমি. হলে, ত্রিভুজটির পরিকেন্দ্র ত্রিভুজাকার ক্ষেত্রের কোথায় অবস্থিত তা লিখি৷

সমাধানঃ
ত্রিভুজের তিনটি বাহুর দৈর্ঘ্য 6 সেমি., 8 সেমি. ও 10 সেমি.
এখন 6²+ 8² = 36 + 64 = 100 = 10²
∴ ইহা একটি সমকোণী ত্রিভুজ যার অতিভুজের দৈর্ঘ্য 10 সেমি.
আমরা জানি, সমকোণী ত্রিভুজের ক্ষেত্রে ত্রিভুজের পরিকেন্দ্র ত্রিভুজের অতিভুজের মধ্যবিন্দুতে অবস্থিত।

উত্তরঃ ত্রিভুজটির পরিকেন্দ্র 10 সেমি. বাহুর মধ্যবিন্দুতে অবস্থিত।

Q11. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ

(ii) ABC সমবাহু ত্রিভুজের AD মধ্যমা এবং G ভরকেন্দ্র। ত্রিভুজটির বাহুর দৈর্ঘ্য 3√3 সেমি. হলে AG-এর দৈর্ঘ্য কত তা লিখি৷

সমাধানঃ
Koshe Dekhi 17 Class 9 ABC ত্রিভুজটি সমবাহু ত্রিভুজ
ABC ত্রিভুজের উচ্চতা = ^√3/₂ × 3√3 সেমি. = 4.5 সেমি.

সমবাহু ত্রিভুজের ক্ষেত্রে মধ্যমা এবং উচ্চতা সমান হয়৷
∴ ABC ত্রিভুজের মধ্যমা, AD = 4.5 সেমি.

আবার ত্রিভুজের ভারকেন্দ্র মধ্যমাকে 2 : 1 অনুপাতে অন্তর্বিভক্ত করে।
∴ AG = ²/₃ × AD
= ²/₃× 4.5 সেমি.
= 3 সেমি.

উত্তরঃ AG এর দৈর্ঘ্য 3 সেমি.

Q11. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ

(iii) একটি ত্রিভুজের কয়টি বিন্দু ত্রিভুজের বাহুগুলি থেকে সমদূরবর্তী তা লিখি৷

উত্তরঃ একটি ত্রিভুজের একটি বিন্দু ত্রিভুজের বাহুগুলি থেকে সমদূরবর্তী৷

Q11. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ

(iv) ABC সমবাহু ত্রিভুজের পাদ ত্রিভুজ DEF; ∠FDA -এর পরিমাপ কত তা লিখি৷

সমাধানঃ

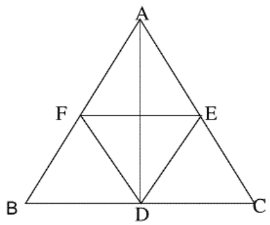
Koshe Dekhi 17 Class 9
যেহেতু, ABC একটি সমবাহু ত্রিভুজ।
∴ ABC ত্রিভুজের পাদ ত্রিভুজ হবে একটি সমবাহু ত্রিভুজ হবে।
সুতরাং, DEF একটি সমবাহু ত্রিভুজ।
∠DFE = 60°

সমবাহু ত্রিভুজের ক্ষেত্রে, AD মধ্যমা ∠BAC কে সমদ্বিখন্ডিত করে
সুতরাং, ∠BAD = 60°/2 = 30°

এখানে, ΔAFE একটি সমবাহু ত্রিভুজ [∵ ΔABC একটি সমবাহু ত্রিভুজ]
∴ ∠AFE = 60°

ΔAFD থেকে পাই,
∠FDA = 180° − ∠FAD − ∠AFD
= 180° − ∠BAD − (∠AFE + ∠DFE)
= 180° − 30° − (60° + 60°)
= 30°

উত্তরঃ ∠FDA = 30°

Q11. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ

(v) ABC সমদ্বিবাহু ত্রিভুজের ∠ABC = ∠ACB এবং মধ্যমা AD = ½ BC। যদি AB = √2 সেমি. হয়, তাহলে ত্রিভুজটির পরিব্যাসার্ধের দৈর্ঘ্য কত তা লিখি।

সমাধানঃ

Koshe Dekhi 17 Class 9
ABC সমদ্বিবাহু ত্রিভুজের D, BC বাহুর মধ্যবিন্দু এবং AD = ½ BC
∴ ∠BAC = 90°
সুতরাং, ABC একটি সমকোণী ত্রিভুজ।
আবার, ABC সমদ্বিবাহু ত্রিভুজের ∠ABC = ∠ACB
∴ AB = AC = √2 সেমি.

ABC সমকোণী সমদ্বিবাহু ত্রিভুজের-
AB² + AC²= BC²
$\Rightarrow BC=\sqrt{\left ( \sqrt{2} \right )^{2}+\left ( \sqrt{2} \right )^{2}}$
$\Rightarrow BC=\sqrt{2+2}=\sqrt{4}=2$ সেমি.

আমরা জানি, সমকোণী ত্রিভুজের পরিব্যসার্ধের দৈর্ঘ্য অতিভুজের অর্ধেক।
∴ ত্রিভুজটির পরিব্যাসার্ধের দৈর্ঘ্য ²/₂ = 1 সেমি.

উত্তরঃ ত্রিভুজটির পরিব্যাসার্ধের দৈর্ঘ্য 1 সেমি.

Koshe Dekhi 17 Class 9

Koshe Dekhi 17 Class 9, Koshe Dekhi 17 Class 9, Koshe Dekhi 17 Class 9, Koshe Dekhi 17 Class 9, Koshe Dekhi 17 Class 9, Koshe Dekhi 17 Class 9, Koshe Dekhi 17 Class 9, Koshe Dekhi 17 Class 9, Koshe Dekhi 17 Class 9, Koshe Dekhi 17 Class 9, Koshe Dekhi 17 Class 9, Koshe Dekhi 17 Class 9, Koshe Dekhi 17 Class 9, Koshe Dekhi 17 Class 9.