Koshe dekhi 7.1 class 10
Koshe dekhi 7.1 class 10
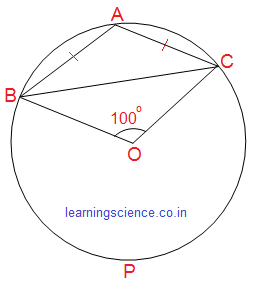
| Q1. ABC সমদ্বিবাহু ত্রিভুজের AB = AC, সমদ্বিবাহু ত্রিভুজটির পরিকেন্দ্র O এবং BC বাহুর যেদিকে A বিন্দু অবস্থিত তার বিপরীত পার্শ্বে কেন্দ্র O অবস্থিত। ∠BOC = 110° হলে, ∠ABC ও ∠ABO এর মান হিসাব করে লিখি।
সমাধান: ∵ BPC বৃত্তচাপের উপর অবস্থিত কেন্দ্রস্থ প্রবৃদ্ধ কোণ ∠BOC ও পরিধিস্থ কোণ ∠BAC ∠BAC = = = = = 130° ∴ ∠BAC = 130°
এখন, ΔABC -এর AB = AC ( প্রশ্নঃ অনুযায়ী) ∴ ∠ACB = ∠ABC (∵ সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের বিপরীত কোণ পরস্পর সমান হয়) মান বসিয়ে পাই- ∴
একইভাবে, ΔBOC -এর OB = OC (একটি বৃত্তের ব্যাসার্ধ) ∴ ∠OBC = ∠OCB মান বসিয়ে পাই- ∴
এখন, ∠ABO = ∠ABC + ∠OBC মান বসিয়ে পাই- ∠ABO = 25° + 40° ∴ ∠ABO = 65° (উত্তর) |
koshe dekhi 7.1 class 10
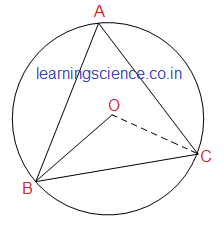
Q2. পাশের চিত্রে ΔABC -এর পরিবৃত্তের কেন্দ্র O এবং ∠AOC = 110°, ∠ABC -এর মান হিসাব করে লিখি।
সমাধান: ∠AOC = 100° ∴ প্রবৃদ্ধ ∠AOC = (360° − 110°) = 250° [প্রবৃদ্ধ ∠AOC + ∠AOC = 360°]
∴ ∠ABC = মান বসিয়ে পাই- ∠ABC = ∴ ∠ABC = 125° (উত্তর) |
koshe dekhi 7.1 class 10
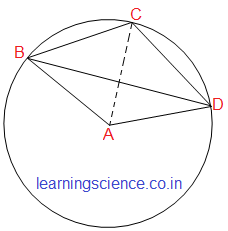
| Q3. O কেন্দ্রীয় বৃত্তের ABCD একটি বৃত্তস্থ চতুর্ভুজ। DC বাহুকে P বিন্দু পর্যন্ত বর্ধিত করা হলো। ∠BCP = 108° হলে, ∠BOD -এর মান হিসাব করে লিখি।
সমাধান: ∵ ∠DCP =180° (D, C ও P একই সরলরেখায় অবস্থিত) ∴ ∠BCD = 180° − ∠DCP মান বসিয়ে পাই- ∠BCD = 180° − 108° ∴ ∠BCD = 72°
এখন, ∵ BAD বৃত্তচাপের উপর অবস্থিত কেন্দ্রস্থ কোণ ∠BOD ও পরিধিস্থ কোণ ∠BCD ∴ ∠BOD = 2 × ∠BCD (কোনো বৃত্তের একই বৃত্তচাপের উপর অবস্থিত কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন হয়) মান বসিয়ে পাই- ∠BOD = 2 × 72° ∴ ∠BOD = 144° (উত্তর) |
koshe dekhi 7.1 class 10
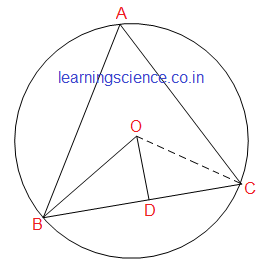
Q4. পাশের চিত্রে O কেন্দ্রীয় বৃত্তের ∠AOD = 40° এবং ∠ACB = 35°, ∠BCO ও ∠BOD -এর মান হিসাব করে লিখি ও উত্তরের সপক্ষে যুক্তি দিই।
সমাধান: ∵ BA বৃত্তচাপের উপর অবস্থিত কেন্দ্রস্থ কোণ ∠AOB ও পরিধিস্থ কোণ ∠ACB ∴ ∠AOB = 2 × ∠ACB (কোনো বৃত্তের একই বৃত্তচাপের উপর অবস্থিত কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন হয়) মান বসিয়ে পাই- ∠AOB = 2 × 35° ∴ ∠AOB = 70°
এখন, ∠BOD = ∠AOB + ∠AOD মান বসিয়ে পাই- ∠BOD = 70° + 40° ∴ ∠BOD = 110° (উত্তর)
আবার, ∠BOC = 180° − ∠BOD ∴ ∠BOC = (180° − 110°) = 70°
এখন, ∵ ΔBOC -এর OB = OC (একটি বৃত্তের ব্যাসার্ধ) ∴ ∠OBC = ∠BCO মান বসিয়ে পাই- ∴ |
koshe dekhi 7.1 class 10
| Q5. পাশের চিত্রের O কেন্দ্রীয় বৃত্তের ∠APB = 80° হলে, ∠AOB ও ∠COD -এর মানের সমষ্টি নির্ণয় করি ও উত্তরের সপক্ষে যুক্তি দিই।
সমাধান: B, C যুক্ত করা হলো। ∵ ΔBPC -এর বহিঃকোণ ∠APB ও অন্তঃস্থ বিপরীত কোণ দুটি হলো ∠PCB ও ∠PBC ∴ ∠PCB + ∠PBC = ∠APB অর্থ্যাৎ, ∠PCB + ∠PBC = 80° …..(i) [∵ ∠APB = 80°]
∵ AB বৃত্তচাপের উপর অবস্থিত কেন্দ্রস্থ ∠AOB ও পরিধিস্থ ∠ACB ∴ ∠AOB = 2 ∠ACB [কোনো বৃত্তের একই বৃত্তচাপের উপর অবস্থিত কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন হয়] অর্থ্যাৎ, ∠AOB = 2 ∠PCB ……(ii) [∠ACB ও ∠PCB একই কোণ]
আবার, ∵ DC বৃত্তচাপের উপর অবস্থিত কেন্দ্রস্থ ∠COD ও পরিধিস্থ ∠DBC ∴ ∠COD = 2 ∠DBC [কোনো বৃত্তের একই বৃত্তচাপের উপর অবস্থিত কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন হয়] অর্থ্যাৎ, ∠COD = 2 ∠PBC ……(iii) [∠DBC ও ∠PBC একই কোণ]
এখন, (ii) ও (iii) নং সমীকরণ দুটিকে যোগ করে পাই – ∠AOB + ∠COD = 2 ∠PCB + 2 ∠PBC = 2 (∠PCB + ∠PBC) = 2 × 80° [(i) নং সমীকরণ ব্যবহার করে পাই] = 160° ∴ ∠AOB + ∠COD = 160° (উত্তর) |
Support Me
If you like my work then you can Support me by contributing a small amount which will help me a lot to grow my channel. It’s a request to all of you. You can donate me through phone pay / Paytm/ Gpay on this number 7980608289 or by the link below :
koshe dekhi 7.1 class 10
| Q6. পাশের ছবির মতো C ও D কেন্দ্রবিশিষ্ট দুটি বৃত্ত অঙ্কন করেছি যারা পরস্পরকে A ও B বিন্দুতে ছেদ করেছে। A বিন্দুগামী একটি সরলরেখা PQ অঙ্কন করেছি যা C কেন্দ্রীয় বৃত্তকে P বিন্দুতে এবং D কেন্দ্রীয় বৃত্তকে Q বিন্দুতে ছেদ করেছে। প্রমাণ করি যে,
(i) ∠PQB = ∠CAD (ii) ∠BPC = ∠BQD.
সমাধান (i): সমাধান (ii): |
koshe dekhi 7.1 class 10
| Q7. ABC ত্রিভুজের পরিকেন্দ্র O; প্রমাণ করি যে, ∠OBC + ∠BAC = 90°.
সমাধান: |
koshe dekhi 7.1 class 10
| Q8. দুটি সমান বৃত্ত একটি অপরটির কেন্দ্রগামী এবং বৃত্তদুটি পরস্পরকে A ও B বিন্দুতে ছেদ করেছে। A বিন্দুগামী সরলরেখা বৃত্ত দুটিকে C ও D বিন্দুতে ছেদ করলে, প্রমাণ করি যে, ΔBCD সমবাহু ত্রিভুজ।
সমাধান: |
koshe dekhi 7.1 class 10
| Q9. ΔABC -এর পরিবৃত্তের কেন্দ্র S এবং AD ⊥ BC হলে, প্রমাণ করি যে, ∠BAD = ∠SAC.
সমাধান: |
koshe dekhi 7.1 class 10
| Q10. O কেন্দ্রীয় একটি বৃত্তের দুটি জ্যা AB ও CD পরস্পরকে P বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, ∠AOD + ∠BOC = 2∠BPC.
যদি ∠AOD ও ∠BOC পরস্পর সম্পূরক হয়, তাহলে প্রমাণ করি যে, জ্যা দুটি পরস্পর লম্ব। সমাধান: |
koshe dekhi 7.1 class 10
| Q11. O কেন্দ্রীয় একটি বৃত্তের AB ও CD দুটি জ্যাকে বর্ধিত করলে তারা পরস্পরকে P বিন্দুতে ছেদ করলে, প্রমাণ করি যে, ∠AOC − ∠BOD = 2∠BPC.
সমাধান: |
koshe dekhi 7.1 class 10
| Q12. ABCD চতুর্ভুজের A বিন্দুকে কেন্দ্র করে একটি বৃত্ত অঙ্কন করা হলো যেটি B, C ও D বিন্দু দিয়ে যায়। প্রমাণ করি যে, সমাধান: |
koshe dekhi 7.1 class 10
| Q13. ΔABC -এর পরিকেন্দ্র O এবং OD, BC বাহুর উপর লম্ব। প্রমাণ করি যে, ∠BOD = ∠BAC.
সমাধান: |
koshe dekhi 7.1 class 10
| Q14. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
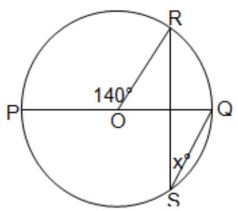
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) : (i) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং PQ ব্যাস হলে, x -এর মান (a) 140° (b) 40° (c) 80° (d) 20° উত্তর : (d) 20° সমাধান: |
| Q14. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) : (ii) পাশের চিত্রে O বৃত্তের কেন্দ্র হলে, x -এর মান (a) 70° (b) 60° (c) 40° (d) 200° উত্তর : (a) 70° সমাধান: |
Support Me
If you like my work then you can Support me by contributing a small amount which will help me a lot to grow my channel. It’s a request to all of you. You can donate me through phone pay / Paytm/ Gpay on this number 7980608289 or by the link below :
| Q14. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) : (iii) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং BC ব্যাস হলে, x -এর মান (a) 60° (b) 50° (c) 100° (d) 80° উত্তর : (b) 50° সমাধান: |
| Q14. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) : (iv) ABC ত্রিভুজের O পরিকেন্দ্র। ∠OAB = 50° হলে, ∠ACB -এর মান (a) 50° (b) 100° (c) 40° (d) 80° উত্তর : (c) 40° সমাধান: |
| Q14. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) : (v) পাশের চিত্রে O বৃত্তের কেন্দ্র হলে, ∠PQR -এর মান (a) 20° (b) 40° (c) 60° (d) 40° উত্তর : (c) 60° সমাধান: |
| 14 (B) সত্য বা মিথ্যা লিখি :
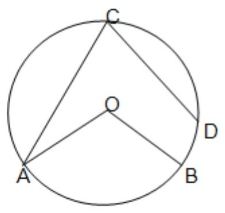
(i) পাশের চিত্রে O বৃত্তের কেন্দ্র হলে, ∠AOB = 2∠ACD. উত্তর : বিবৃতিটি মিথ্যা সমাধান: এক্ষেত্রে, ∠AOB হলো AB বৃত্তচাপের উপর অবস্থিত কেন্দ্রস্থ কোণ এবং ∠ACD হলো AD বৃত্তচাপের উপর অবস্থিত পরিধিস্থ কোণ।
|
| 14 (B) সত্য বা মিথ্যা লিখি :
(ii) ABC ত্রিভুজাকার ক্ষেত্রের ভিতর O বিন্দু এমনভাবে অবস্থিত যে OA = OB এবং ∠AOB = 2∠ACB; O বিন্দুকে কেন্দ্র করে OA দৈর্ঘ্যের ব্যাসার্ধ নিয়ে বৃত্ত অঙ্কন করলে C বিন্দু বৃত্তের উপর অবস্থিত হবে। উত্তর : বিবৃতিটি সত্য সমাধান: আবার, যেহেতু O হলো ΔABC -এর পরিকেন্দ্র। সুতরাং, ∠AOB হবে বৃত্তটির একটি কেন্দ্রস্থ কোণ যা AB বৃত্তচাপের উপর অবস্থিত। আবার, যেহেতু ∠ACB কোনটিও AB বৃত্তচাপের উপর অবস্থিত এবং ∠AOB = 2∠ACB, তাই ∠ACB হবে O কেন্দ্রীয় বৃত্তটির একটি পরিধিস্থ কোণ। সুতরাং, C বিন্দুটি বৃত্তের উপর অবস্থিত। (উল্লেখ্য, কোনো বৃত্তের একই বৃত্তচাপের উপর অবস্থিত কেন্দ্রস্থ কোণ পরিধিস্থ কোণের দ্বিগুন হয়) |
| 14 (C) শূন্যস্থান পূরণ করি :
(i) একই চাপের উপর অবস্থিত বৃত্তস্থ কোণ কেন্দ্রস্থ কোণের _______। উত্তর : একই চাপের উপর অবস্থিত বৃত্তস্থ কোণ কেন্দ্রস্থ কোণের অর্ধেক। |
| 14 (C) শূন্যস্থান পূরণ করি :
(ii) O কেন্দ্রীয় বৃত্তে AB ও AC জ্যা দুটির দৈর্ঘ্য সমান। ∠APB ও ∠DQC বৃত্তস্থ কোণ হলে, কোণ দুটির মান ________। উত্তর : O কেন্দ্রীয় বৃত্তে AB ও AC জ্যা দুটির দৈর্ঘ্য সমান। ∠APB ও ∠DQC বৃত্তস্থ কোণ হলে, কোণ দুটির মান সমান। ব্যাখ্যা : একই বৃত্তের দুটি সমান দৈর্ঘ্যের জ্যা সমান পরিমাপের বৃত্তচাপ সৃষ্টি করে এবং সমান দৈর্ঘ্যের বৃত্তচাপ দ্বারা গঠিত সকল বৃত্তস্থ কোণের মান সমান হয়। |
| 14 (C) শূন্যস্থান পূরণ করি :
(iii) একটি সমবাহু ত্রিভুজের পরিবৃত্তের কেন্দ্র O হলে, যে-কোনো একটি বাহু দ্বারা উৎপন্ন সম্মুখ কেন্দ্রস্থ কোণের মান _________। উত্তর : একটি সমবাহু ত্রিভুজের পরিবৃত্তের কেন্দ্র O হলে, যে-কোনো একটি বাহু দ্বারা উৎপন্ন সম্মুখ কেন্দ্রস্থ কোণের মান 120° ব্যাখ্যা: |
Support Me
If you like my work then you can Support me by contributing a small amount which will help me a lot to grow my channel. It’s a request to all of you. You can donate me through phone pay / Paytm/ Gpay on this number 7980608289 or by the link below :
| Q15. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)
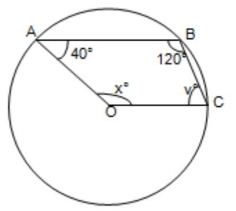
(i) পাশের চিত্রে O বৃত্তের কেন্দ্র। ∠OAB = 40°, ∠ABC = 120°, ∠BCO = y° এবং ∠COA = x° হলে, x ও y -এর মান নির্ণয় করি। উত্তর : x = 120° এবং y = 80° সমাধান: |
| Q15. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)
(ii) ABC ত্রিভুজের পরিকেন্দ্র O এবং D বিন্দু BC বাহুর মধ্যবিন্দু। ∠BAC = 40° হলে, ∠BOD -এর মান নির্ণয় করি। উত্তর : ∠BOD = 40° সমাধান: |
| Q15. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)
(iii) O কেন্দ্রীয় বৃত্তের উপর A, B, C তিনটি বিন্দু এমনভাবে অবস্থিত যে AOCB একটি সামান্তরিক। ∠AOC -এর মান নির্ণয় করি। উত্তর : ∠AOC = 120° সমাধান: |
| Q15. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)
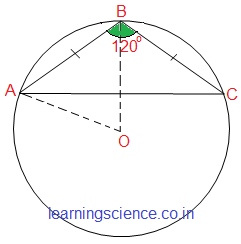
(iv) ABC সমদ্বিবাহু ত্রিভুজের পরিবৃত্তের কেন্দ্র O এবং ∠ABC = 120°; বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5 সেমি. হলে, AB বাহুর দৈর্ঘ্য নির্ণয় করি। উত্তর : AB বাহুর দৈর্ঘ্য 5 সেমি. সমাধান: |
| Q15. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)
(v) A ও B কেন্দ্রীয় বৃত্তদ্বয় C এবং D বিন্দুতে ছেদ করে। A কেন্দ্রীয় বৃত্তের উপর অপর বৃত্তের কেন্দ্র B অবস্থিত। ∠CQD = 70° হলে, ∠CPD -এর মান নির্ণয় করি। উত্তর : ∠CPD = 40° সমাধান: |
koshe dekhi 7.1 class 10
Support Me
If you like my work then you can Support me by contributing a small amount which will help me a lot to grow my Website. It’s a request to all of you. You can donate me through phone pay / Paytm/ Gpay on this number 7980608289 or by the link below :
and visit Our website : learningscience.co.in
গণিত প্রকাশ (দশম শ্রেণী) সম্পূর্ণ সমাধান
গণিত প্রকাশ (নবম শ্রেণী) সম্পূর্ণ সমাধান
গণিত প্রভা (ষষ্ঠ শ্রেণী) সম্পূর্ণ সমাধান