Koshe Dekhi 9 Class 9

Q1. ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D; D বিন্দু দিয়ে CA এবং BA বাহুর সমান্তরাল সরলরেখাংশ BA এবং CA বাহুকে যথক্রমে E ও F বিন্দুতে ছেদ করে৷ প্রমাণ করি যে, EF = ½ BC

সমাধানঃ

বিশেষ নির্বচনঃ ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D; D বিন্দু দিয়ে CA এবং BA বাহুর সমান্তরাল সরলরেখাংশ BA এবং CA বাহুকে

যথাক্রমে E ও F বিন্দুতে ছেদ করে৷

প্রমাণ করতে হবে যে, EF = ½ BC

প্রমাণঃ ΔABC -এর BC বাহুর মধ্যবিন্দু D এবং DE || CA

∴ E, AB বাহুর মধ্যবিন্দু।

আবার, ΔABC -এর BC বাহুর মধ্যবিন্দু D এবং DF || BA

∴ F, AC বাহুর মধ্যবিন্দু।

এখন, ΔABC -এর AB বাহুর মধ্যবিন্দু E এবং AC বাহুর মধ্যবিন্দু F.

∴ EF = ½ BC [প্রমানিত]

Q2. D এবং E বিন্দুদ্বয় যথাক্রমে ABC ত্রিভুজের AB এবং AC বাহুর উপর এমন ভাবে অবস্থিত যে, AD = ¼ AB এবং AE = ¼ AC; প্রমাণ করি যে, DE || BC এবং DE = ¼ BC

সমাধানঃ

Koshe Dekhi 9 Class 9

বিশেষ নির্বচনঃ ΔABC এর D এবং E বিন্দুদ্বয় এমন ভাবে অবস্থিত যে, AD = ¼ AB এবং AE = ¼ AC

অঙ্কনঃ AB বাহুর মধ্যবিন্দু F এবং AC বাহুর মধ্যবিন্দু G নেওয়া হল এবং F, G যুক্ত করা হল৷

প্রমাণঃ ΔABC এর AB বাহুর মধ্যবিন্দু F এবং AC বাহুর মধ্যবিন্দু G। [অঙ্কনানুসারে]

∴ FG || BC এবং FG = ½ BC

F, AB বাহুর মধ্যবিন্দু এবং AE = ¼ AC

∴ AD = ½ AF

আবার, G, AC বাহুর মধ্যবিন্দু এবং AD = ¼ AB

∴ AE = ½ AG

সুতরাং, ΔAFG এর AF বাহুর মধ্যবিন্দু D এবং AG বাহুর মধ্যবিন্দু E

∴ DE || FG

অর্থাৎ DE || BC [∵ FG || BC] [প্রমানিত]

এবং DE = ½ FG

= ½ × ½ BC [∵ FG = ½ BC]

= ¼ BC

∴ DE = ¼ BC [প্রমানিত]

Q3. X এবং Z যথাক্রমে PQR ত্রিভুজের QR এবং QP বাহুর মধ্যবিন্দু৷ QP বাহুকে S বিন্দু পর্যন্ত এমনভাবে বর্ধিত করা হল যাতে PS = ZP হয়৷ SX, PR বাহুকে Y বিন্দুতে ছেদ করে৷ প্রমাণ করি যে, PY = ¼ PR.

সমাধানঃ

Koshe Dekhi 9 Class 9

বিশেষ নির্বচনঃ POR ত্রিভুজের X, QR বাহুর মধ্যবিন্দু এবং Z, QP বাহুর মধ্যবিন্দু। QP কে P পর্যন্ত বর্ধিত করা হল এবং PS = ZP.

SX, PR বাহুকে Y বিন্দুতে ছেদ করে৷

প্রমান করতে হবে যে, PY = ¼ PR

অঙ্কনঃ X, Z যুক্ত করা হল৷

প্রমাণঃ ΔPQR এর মধ্যে,

X, QR বাহুর মধ্যবিন্দু এবং Z, QP বাহুর মধ্যবিন্দু।

∴ ZX = ½ PR ….(1)

আবার, ΔSZX এর মধ্যে,

ZX || PY [∵ ZX || PR]

এবং P, ZS বাহুর মধ্যবিন্দু [∵ PS = ZP]

∴ PY = ½ ZX

বা, PY = ½ × ½ PR [(1) নং থেকে পাই]

∴ PY = ¼ PR [প্রমানিত]

Q4. প্রমাণ করি যে, একটি সমন্তরিকের বাহুগুলির মধ্যবিন্দুগুলি পরপর যুক্ত করলে যে চতুর্ভুজ গঠিত হয়, সেটি একটি সামন্তরিক।

সমাধানঃ

Koshe Dekhi 9 Class 9

বিশেষ নির্বচনঃ ধরি, ABCD একটি সামান্তরিক। P, Q, R ও S হল যথাক্রমে AB, BC, CD ও DA বাহুর মধ্যবিন্দু।

প্রমান করতে হবে যে, PQRS একটি সামান্তরিক।

অঙ্কনঃ AC কর্ণ অঙ্কন করলাম৷

প্রমাণঃ ΔCDA এর –

R, CD বাহুর মধ্যবিন্দু এবং S, DA বাহুর মধ্যবিন্দু

∴ SR || AC এবং SR = ½ AC

আবার, ΔABC এর –

P, AB বাহুর মধ্যবিন্দু এবং Q, BC বাহুর মধ্যবিন্দু

∴ PQ || AC এবং PQ = ½ AC

যেহেতু, SR || AC এবং PQ || AC

∴ PQ || SR

আবার, যেহেতু SR = ½ AC এবং PQ = ½ AC

∴ PQ = SR

∴ আমরা পেলাম, PQRS চতুর্ভুজের PQ ||SR এবং PQ = SR.

∴ PQRS একটি সামান্তরিক। [প্রমানিত]

Q5. প্রমাণ করি যে, একটি আয়তকার চিত্রের বাহুগুলির মধ্যেবিন্দুগুলি পরপর যুক্ত হয়ে যে চতুর্ভুজটি গঠিত হয়, সেটি একটি রম্বস, কিন্তু বর্গাকার চিত্র নয়৷

সমাধানঃ

Koshe Dekhi 9 Class 9

বিশেষ নির্বচনঃ ধরি, ABCD একটি আয়তক্ষেত্র। P, Q, R ও S হল যথাক্রমে AB, BC, CD ও DA বাহুর মধ্যবিন্দু।

প্রমান করতে হবে যে, PQRS একটি রম্বস কিন্তু বৰ্গক্ষেত্র নয়৷

অঙ্কনঃ AC কর্ণ অঙ্কন করলাম৷

প্রমানঃ ΔCDA এর –

R, CD বাহুর মধ্যবিন্দু এবং S, DA বাহুর মধ্যবিন্দু

∴ SR || AC এবং SR = ½ AC ……(1)

আবার, ΔABC এর –

P, AB বাহুর মধ্যবিন্দু এবং Q, BC বাহুর মধ্যবিন্দু

∴ PQ || AC এবং PQ = ½ AC …..(2)

(1) নং ও (2) নং থেকে পাই

PQ || SR এবং PQ = ½ SR

∴ PQRS একটি সামান্তরিক।

এখন যেহেতু ABCD একটি আয়তক্ষেত্র

∴ AD = BC

বা, ½ AD = ½ BC

∴ AS = BQ ….(3) [∵ S, AD -এর মধ্যবিন্দু এবং Q, BC -এর মধ্যবিন্দু]

ΔAPS এবং ΔBPQ এর-

AP = BP [∵ P, BC বাহুর মধ্যবিন্দু]

AS = BQ [(3) নং থেকে পাই]

∠PAS = ∠PBQ [উভয়েই সমকোণ]

∴ ΔAPS ≅ ΔBPQ [S-A-S সর্বসমতার শর্তানুসারে]

∴ SP = PQ [সর্বসম ত্রিভুজের অনুরূপ বাহু]

∠APS = ∠BPQ [সর্বসম ত্রিভুজের অনুরূপ কোণ]

এখন যেহেতু PQRS সামান্তরিকের SP = PQ

∴ PQRS সামান্তরিকটি একটি রম্বস৷

এখন সমকোণী ΔAPS এর

∠B সমকোণ এবং AS ≠ AP [∵ AB ≠ AD]

∴ ∠APS ≠ ∠BPQ

∴ ∠APS ≠ 45°

PQRS রম্বসের

∠SPQ = 180° − ∠APS − ∠BPQ

= 180° − 2∠APS [∵ ∠APS = ∠BPQ]

≠ 90° [∵ ∠APS ≠ 45°]

PQRS একটি রম্বস কিন্তু বর্গক্ষেত্র নয়৷ [প্রমানিত]

Q6. প্রমাণ করি যে, একটি বর্গাকার চিত্রের বাহুগুলির মধ্যবিন্দুগুলি পরপর যুক্ত হয়ে যে চতুর্ভুজটি গঠিত হয়, সেটি একটি বর্গাকার চিত্ৰ৷

সমাধানঃ

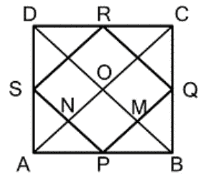
Koshe Dekhi 9 Class 9

বিশেষ নির্বচনঃ ABCD একটি বর্গক্ষেত্ৰ৷ P, Q, R ও S হল যথাক্রমে AB, BC, CD ও DA বাহুর মধ্যবিন্দু।

প্রমান করতে হবে যে, PQRS একটি বর্গক্ষেত্ৰ

অঙ্কনঃ AC, BD কর্ণ অঙ্কন করলাম৷

প্রমানঃ ΔCDA এর –

R, CD বাহুর মধ্যবিন্দু এবং S, DA বাহুর মধ্যবিন্দু

∴ SR || AC এবং SR = ½ AC ……(1)

আবার, ΔABC এর –

P, AB বাহুর মধ্যবিন্দু এবং Q, BC বাহুর মধ্যবিন্দু

∴ PQ || AC এবং PQ = ½ AC …..(2)

(1) নং ও (2) নং থেকে পাই

PQ || SR এবং PQ = ½ SR

∴ PQRS একটি সামান্তরিক।

ΔABD এর –

P, AB বাহুর মধ্যবিন্দু এবং S, DA বাহুর মধ্যবিন্দু

∴ PS || BD এবং PS = ½ BD ….(3)

ABCD একটি বর্গক্ষেত্র যার AC = BD

বা, ½ AC = ½ BD

∴ PQ = PS

PQRS সামান্তরিকের PQ = PS

PQRS সামান্তরিকটি একটি রম্বস।

এখন PMON চতুর্ভুজের

PM || ON [∵ PQ || AC]

NP || OM [∵ PS || BD]

∴ PMON একটি সামান্তরিক

PMON সামান্তরিকের ∠MON = ∠MPN

আবার, ∠MON = ∠AOB = 90° [∵ বর্গক্ষেত্রের কর্ণদ্বয় সমকোণে সমদ্বিখন্ডিত করে]

∴ ∠MPN = 90°

∴ PQRS রম্বসের ∠SPQ = ∠MPN = 90°

∴PQRS রম্বসটি একটি বর্গক্ষেত্র। [প্রমানিত]

Q7. প্রমাণ করি যে, একটি রম্বসের বাহুগুলির মধ্যবিন্দুগুলি পরপর যুক্ত হয়ে যে চতুর্ভুজটি গঠিত হয়, সেটি একটি আয়তকার চিত্ৰ৷

সমাধানঃ

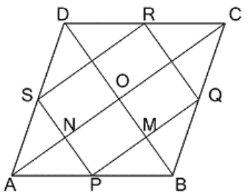
Koshe Dekhi 9 Class 9

বিশেষ নির্বচনঃ ABCD একটি রম্বস৷ P, Q, R ও S হল যথাক্রমে AB, BC, CD ও DA বাহুর মধ্যবিন্দু।

প্রমান করতে হবে যে, PQRS একটি আয়তক্ষেত্র৷

অঙ্কনঃ AC, BD কর্ণ অঙ্কন করলাম৷

প্রমানঃ ΔCDA এর –

R, CD বাহুর মধ্যবিন্দু এবং S, DA বাহুর মধ্যবিন্দু

∴ SR || AC এবং SR = ½ AC ……(1)

আবার, ΔABC এর –

P, AB বাহুর মধ্যবিন্দু এবং Q, BC বাহুর মধ্যবিন্দু

∴ PQ || AC এবং PQ = ½ AC …..(2)

(1) নং ও (2) নং থেকে পাই

PQ || SR এবং PQ = ½ SR

∴ PQRS একটি সামান্তরিক।

ΔABD এর –

P, AB বাহুর মধ্যবিন্দু এবং S, DA বাহুর মধ্যবিন্দু

∴ PS || BD এবং PS = ½ BD ….(3)

এখন PMON চতুর্ভুজের

PM || ON [∵ PQ || AC]

NP || OM [∵ PS || BD]

∴ PMON একটি সামান্তরিক

PMON সামান্তরিকের ∠MON = ∠MPN

আবার, ∠MON = ∠AOB = 90° [∵ বর্গক্ষেত্রের কর্ণদ্বয় সমকোণে সমদ্বিখন্ডিত করে]

∴ ∠MPN = 90°

∴ PQRS সামান্তরিকের ∠SPQ = ∠MPN = 90°

∴ PQRS সামান্তরিকটি একটি আয়তক্ষেত্র । [প্রমানিত]

Q8. ABC ত্রিভুজের AB এবং AC বাহুর মধ্যবিন্দু যথাক্রমে D এবং E; P এবং Q যথাক্রমে CD ও BD এর মধ্যবিন্দু। প্রমাণ করি যে, BE এবং PQ পরস্পরকে সমদ্বিখন্ডিত করে৷

সমাধানঃ

Koshe Dekhi 9 Class 9

বিশেষ নির্বচনঃ ABC ত্রিভুজের AB এবং AC বাহুর মধ্যবিন্দু যথাক্রমে D এবং E; P এবং Q যথাক্রমে CD এবং BD –এর মধ্যবিন্দু।

অঙ্কনঃ D, E ও E, P যুক্ত করলাম৷

প্রমাণঃ ΔABC এর –

D, AB বাহুর মধ্যবিন্দু এবং E, AC বাহুর মধ্যবিন্দু

∴ DE || BC এবং DE = ½ BC ….(1)

ΔDBC এর –

P, BD বাহুর মধ্যবিন্দু এবং Q, CD বাহুর মধ্যবিন্দু

∴ PQ || BC এবং PQ = ½ BC …..(2)

(1) নং ও ( 2 ) নং থেকে পাই,

DE || PQ এবং DE = PQ

PQDE চতুর্ভুজের DE || PQ এবং DE = PQ

∴ PQDE চতুর্ভুজটি একটি সামন্তরিক।

ΔBDE এর Q, BD -এর মধ্যবিন্দু এবং QM || DE [∵ DE || PQ]

∴ M, PQ বাহুর মধ্যবিন্দু এবং QM = ½ DE

বা, QM = ½ PQ [∵ DE = PQ]

∴ M, PQ বাহুর মধ্যবিন্দু এবং M, BE বাহুর মধ্যবিন্দু

∴ BE এবং PQ পরস্পরকে সমদ্বিখন্ডিত করে। [প্রমানিত]

Q9. ABC ত্রিভুজের ∠ABC এর সমদ্বিখন্ডকের উপর AD লম্ব। D বিন্দু দিয়ে BC বাহুর সমান্তরাল সরলরেখাংশ DE টানা হল যা AC বাহুকে E বিন্দুতে ছেদ্ করে। প্রমাণ করি যে, AE = EC

সমাধানঃ

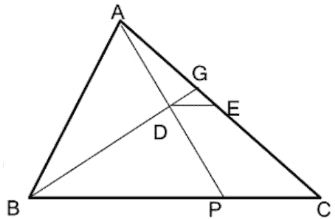
Koshe Dekhi 9 Class 9

বিশেষ নির্বচনঃ ABC ত্রিভুজের ∠ABC এর সমদ্বিখন্ডকের উপর AD লম্ব৷ D বিন্দু দিয়ে BC বাহুর সমান্তরাল সরলরেখাংশ DE টানা হল যা AC বাহুকে E বিন্দুতে ছেদ্ করে৷

প্রমাণ করতে হবে যে, AE = EC

অঙ্কনঃ AD বর্ধিত করা হল যা BC বাহুকে P বিন্দুতে ছেদ করে৷

প্রমানঃ যেহেতু, AP ⊥ BG

∴ ∠ADB = ∠BDP = 90° ….(1)

সুতরাং, ΔABD এবং ΔPBD একটি সমকোণী ত্রিভুজ

∴ ∠BAD = 90° − ∠ABD এবং ∠BPD = 90° − ∠PBD

আবার, ∠ABD = ∠PBD [BG, ∠ABC এর সমদ্বিখন্ডক]

∴ ∠BAD = ∠BPD …..(2)

ΔABD এবং ΔPBD এর –

∠ADB = ∠BDP [(1) নং থেকে পাই]

∠BAD = ∠BPD [(2)নং থেকে পাই]

BD সাধারণ বাহু

∴ ΔABD ≅ ΔPBD [সর্বসমতার A-A-S শর্তানুসারে]

AD = DP [সর্বসম ত্রিভুজের অনুরূপ বাহু]

অর্থাৎ, D, AP বাহুর মধ্যবিন্দু

ΔAPC এর D, AP বাহুর মধ্যবিন্দু এবং DE || PC [∵ DE || BC]

∴ E, AC বাহুর মধ্যবিন্দু

সতরাং, AE = EC [প্রমানিত]

Q10. ABC ত্রিভুজের AD মধ্যমা৷ B ও C বিন্দু দিয়ে AD -এর সমান্তরাল সরলরেখাংশ BR এবং CT টানা হল যারা বর্ধিত BA এবং CA বাহুর সঙ্গে যথাক্রমে T এবং R বিন্দুতে মিলিত হয়৷ প্রমাণ করি যে, ${\color{Blue} \frac{1}{AD}=\frac{1}{RB}+\frac{1}{TC}}$

সমাধানঃ

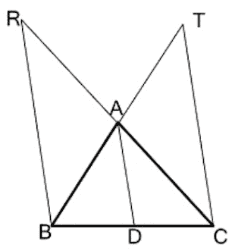
Koshe Dekhi 9 Class 9

বিশেষ নির্বচনঃ ABC ত্রিভুজের AD মধ্যমা৷ AD || RB এবং AD || TC

প্রমাণ করতে হবে যে, $\frac{1}{AD}=\frac{1}{RB}+\frac{1}{TC}$

প্রমানঃ ΔBCR ত্রিভুজের D, BC বাহুর মধ্যবিন্দু এবং AD || RB

∴ AD = ½ RB ….(1)

আবার, BCT ত্রিভুজের D, BC বাহুর মধ্যবিন্দু এবং AD || TC

∴ AD = ½ TC ….(2)

(1) নং ও ( 2 ) নং থেকে পাই

½ RB = ½ TC

∴ RB = TC

এখন, $\frac{1}{AD}=\frac{1}{\frac{1}{2}RB}=\frac{2}{RB}=\frac{1}{RB}+\frac{1}{RB}$

বা, $\frac{1}{AD}=\frac{1}{RB}+\frac{1}{TC}\; {\color{Blue} \left [ \because RB=TC \right ]}$

∴ $\frac{1}{AD}=\frac{1}{RB}+\frac{1}{TC}$ [প্রমানিত]

Q11. ABCD ট্রাপিজিয়ামের AB || DC এবং AB>DC; E ও F যথাক্রমে কর্ণদ্বয় AC ও BD এর মধ্যবিন্দু। প্রমাণ করি যে, EF = ½(AB − DC)

সমাধানঃ

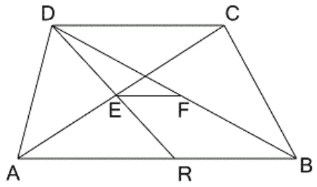
Koshe Dekhi 9 Class 9

বিশেষ নির্বচনঃ ABCD ট্রাপিজিয়ামের AB || DC এবং AB>DC; E ও F যথাক্রমে কর্ণদ্বয় AC ও BD এর মধ্যবিন্দু।

অঙ্কনঃ D, E যোগ করলাম৷ বর্ধিতাংশ DE, AB বাহুকে R বিন্দুতে ছেদ করে৷

প্রমানঃ ΔAER এবং ΔCED এর –

∠AER = বিপ্রতীপ ∠DEC

∠EAR = একান্তর ∠EDC [∵ AD||BC এবং DR ছেদক]

AE = EC [∵ E, AC বাহুর মধ্যবিন্দু]

∴ ΔAER ≅ ΔCED [সর্বসমতার A-A-S শর্তানুসারে]

AR = DC [সর্বসম ত্রিভুজের অনুরূপ বাহু] ….(1)

এবং DE = ER [সর্বসম ত্রিভুজের অনুরূপ বাহু]

∴ E, DR বাহুর মধ্যবিন্দু

এখন ΔBDR এর E, DR বাহুর মধ্যবিন্দু এবং F, BD বাহুর মধ্যবিন্দু

∴ EF = ½ RB

= ½ (AB − AR)

= ½ (AB − DC) [(1)নং থেকে পাই]

∴ EF = ½ (AB − DC) [প্রমানিত]

Q12. AB সরলরেখাংশের মধ্যবিন্দু C এবং PQ যেকোনো একটি সরলরেখা৷ A, B ও C বিন্দু থেকে PQ সরলরেখার ক্ষুদ্রতম দূরত্ব যথাক্রমে AR, BS এবং CT; প্রমাণ করি যে, AR + BS = 2 CT

সমাধানঃ

Koshe Dekhi 9 Class 9

বিশেষ নির্বচনঃ AB সরলরেখাংশের মধ্যবিন্দু C এবং PQ যেকোনো একটি সরলরেখা৷ A, B ও C বিন্দু থেকে PQ সরলরেখার ক্ষুদ্রতম দূরত্ব যথাক্রমে AR, BS ও CT.

প্রমাণ করতে হবে যে, AR + BS = 2 CT

প্রমানঃ যেহেতু, AR, TC ও BS এরা প্রত্যেকেই A, B ও C বিন্দু থেকে PQ সরলরেখার ক্ষুদ্রতম দূরত্ব।

∴ AR, TC ও BS এরা প্রত্যেকেই পরস্পর সমান্তরাল

সুতরাং, AR || CT, BS || CT এবং AR || BS

∴ ARSB একটি ট্রাপিজিয়াম

ARSB ট্রাপিজিয়ামের C, AB বাহুর মধ্যবিন্দু এবং AR || BS

∴ T, RS বাহুর মধ্যবিন্দু এবং CT = ½ (AR + BS)

∴ AR + BS = 2 CT [প্রমানিত]

Q13. ABC ত্রিভুজের BC বাহুর মধ্যবিন্দু D; A বিন্দু দিয়ে PQ যেকোনো একটি সরলরেখা। B, C এবং D বিন্দু থেকে PQ সরলরেখার উপর লম্ব যথাক্রমে BL, CM এবং DN; প্ৰমাণ করি যে, DL = DM.

সমাধানঃ

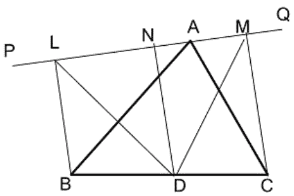
Koshe Dekhi 9 Class 9

প্রমানঃ BL, CM এবং DN প্রত্যেকেই PQ সরলরেখার উপর লম্ব৷

সুতরাং, তারা পরস্পর সমান্তরাল৷

∴ BL || DN || CN

∴ BCML একটি ট্রাপিজিয়াম।

BCML ট্রাপিজিয়ামের DN || CN এবং D, BC বাহু মধ্যবিন্দু৷

∴ N, LM বাহুর মধ্যবিন্দু

ΔDNL এবং ΔDNM এর –

LN = NM [∵ N, LM বাহুর মধ্যবিন্দু]

∠DNL = ∠DNM [DN ⊥ PQ]

DN সাধারণ বাহু

∴ ΔDNL ≅ ΔDNM [সর্বসমতার S-A-S শর্তানুসারে]

∴ DL = DM [সর্বসম ত্রিভুজের অনুরূপ বাহু] [প্রমানিত]

Q14. ABCD একটি বর্গাকার চিত্র। AC এবং BD কর্ণদ্বয় Oবিন্দুতে ছেদ করে৷ ∠BAC এর সমদ্বিখন্ডক BO-কে P বিন্দুতে এবং BC -কে Q বিন্দুতে ছেদ করে৷ প্রমাণ করি যে, OP= ½ CQ.

সমাধানঃ

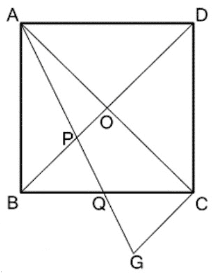
Koshe Dekhi 9 Class 9

বিশেষ নির্বচনঃ ABCD বর্গক্ষেত্রের AC এবং BD কর্ণদ্বয় ০ বিন্দুতে ছেদ করে৷ <BAC এর সমদ্বিখন্ডক BO-কে P বিন্দুতে এবং BC কে Q বিন্দুতে ছেদ করে৷

প্রমাণ করতে হবে যে, OP= ½ CQ

অঙ্কন: AQ কে বর্ধিত করা হল। C বিন্দু থেকে OB এর সমান্তরাল সরলরেখা অঙ্কন করলাম যা বর্ধিত AQ কে G বিন্দুতে ছেদ করেছে।

প্রমানঃ AGC ত্রিভুজের O, AC বাহুর মধ্যবিন্দু এবং OP || CG [অঙ্কনানুসারে, OB || CG]

∴ OP = ½ CG …..(1)

ABCD বর্গক্ষেত্রের ∠ABC = 90°, ∠BCD = 90°

ধরি, ∠BAQ = ∠CAQ = θ

ΔABQ থেকে পাই,

∠BQA = 180° − ∠ABC − ∠BAQ

বা, ∠BQA = 180° − 90° − θ

∴ ∠BQA = 90° − θ

∴ ∠GQC = বিপ্রতীপ ∠BQA = 90° − θ

যেহেতু ∠AOP = 90°

সুতরাং, ΔAOQ একটি সমকোণী ত্রিভুজ

∴ ∠APO = 90° − ∠PAO

= 90° − ∠CAQ

= 90° − θ

আবার, ∠PGC = অনুরূপ ∠APO [∵ OP || CG এবং AG ছেদক]

= 90° − θ

∴ ∠QGC = 90° − θ

GQC ত্রিভুজের ∠GQC = 90° − θ এবং ∠QGC = 90° − θ

∴ ∠GQC = ∠QGC

সুতরাং, CQ = CG ….(2)

(1) নং ও ( 2 ) নং থেকে পাই

OP = ½ CQ [প্রমানিত]

Q15. বহু বিকল্পীয় প্রশ্ন (MCQ):

(i) PQR ত্রিভুজের ∠PQR = 90° এবং PR = 10 সেমি.৷ PR বাহুর মধ্যবিন্দু S হলে, QS এর দৈর্ঘ্য –

(a) 4 সেমি.

(b) 5 সেমি.

(d) 3 সেমি.

উত্তরঃ (b) 5 সেমি.

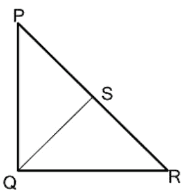
Koshe Dekhi 9 Class 9

PR = 10 সেমি.

∠PQR = 90° এবং অতিভুজ PR বাহুর মধ্যবিন্দু S হলে

QS = ½ PR = ½ × 10 সেমি. = 5 সেমি.

উত্তরঃ (b) 5 সেমি.

Q15. বহু বিকল্পীয় প্রশ্ন (MCQ):

(ii) ABCD ট্রাপিজিয়ামের ABIIDC এবং AB = 7 সেমি ও DC = 5 সেমি.। AD ও BC বাহুর মধ্যবিন্দু যথাক্রমে E ও F হলে, EF এর দৈর্ঘ্য –

(a) 5 সেমি.

(b) 7 সেমি.

(d) 12 সেমি.

উত্তরঃ (c) 6 সেমি.

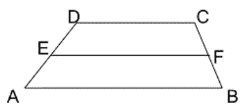
Koshe Dekhi 9 Class 9

E, AD বাহুর মধ্যবিন্দু এবং F, BC বাহুর মধ্যবিন্দু

∴ EF = ½(AB + DC)

= ½ (7 + 5) সেমি.

= 6 সেমি.

উত্তরঃ (c) 6 সেমি.

Q15. বহু বিকল্পীয় প্রশ্ন (MCQ):

(iii) ABC ত্রিভুজের AD মধ্যমার মধ্যবিন্দু E; বর্ধিত BE, AC কে F বিন্দুতে ছেদ করে৷ AC = 10.5 সেমি হলে, AF এর দৈর্ঘ্য –

(a) 3 সেমি.

(b) 5 সেমি.

(d) 3.5 সেমি.

উত্তরঃ (d) 3.5 সেমি.

Koshe Dekhi 9 Class 9

ABC ত্রিভুজের AD মধ্যমার মধ্যবিন্দু E; বর্ধিত BE, AC কে F বিন্দুতে ছেদ করলে

AF = 1/3 AC

= 1/3 × 10.5 সেমি.

= 3.5 সেমি.

উত্তরঃ (d) 3.5 সেমি.

Q15. বহু বিকল্পীয় প্রশ্ন (MCQ):

(iv) ABC ত্রিভুজের BC, CA ও AB বাহুর মধ্যবিন্দু যথাক্রমে D, E ও F; BE ও DF, X বিন্দুতে এবং CF ও DE, Y বিন্দুতে ছেদ করলে, XY এর দৈর্ঘ্য সমান –

(a) ¹/₂ BC

(b) ¹/₄ BC

(d) ¹/₈ BC

উত্তরঃ (b) ¹/₄ BC

Koshe Dekhi 9 Class 9

ABC ত্রিভুজের AB বাহুর মধ্যবিন্দু F এবং AC বাহুর মধ্যবিন্দু E

∴ EF = ½ BC

আবার, BDEF এবং DCEF উভয়েই সামান্তরিক

∴ DF বাহুর মধ্যবিন্দু X এবং DE বাহুর মধ্যবিন্দু Y

∴ XY = ½ EF

= ½ × ½ BC

= ¼ BC

উত্তরঃ (b) ¹/₄ BC

Q15. বহু বিকল্পীয় প্রশ্ন (MCQ):

(v) ABCD সামান্তরিকের BC বাহুর মধ্যবিন্দু E; DE এবং বর্ধিত AB, F বিন্দুতে মিলিত হয়৷ AF -এর দৈর্ঘ্য সমান –

(a) ³/₂ AB

(b) 2 AB

(d) ⁵/₄ AB

উত্তরঃ (b) 2 AB

Koshe Dekhi 9 Class 9

ΔBEF এবং ΔDCE এর মধ্যে

∠ BEF = বিপ্রতীপ ∠CED

∠BFE = একান্তর ∠CDE [∵ AF || DC এবং DF ছেদক]

BE = EC [∵ E, BC বাহুর মধ্যবিন্দু]

∴ ΔBEF ≅ ΔDCE [সর্বসমতার A-A-S শর্তানুসারে]

∴ BF = CD [সর্বসম ত্রিভুজের অনুরূপ বাহু]

আবার, AB = CD [∵ ABCD একটি সামান্তরিক]

∴ BF = AB

AF = AB + BF

= AB + AB

= 2 AB

উত্তরঃ (b) 2 AB

Q16. সংক্ষিপ্ত প্রশ্নঃ

(i) ABC ত্রিভুজের AD এবং BE মধ্যমা এবং BE -এর সমান্তরাল সরলরেখা DF, AC বাহুর সঙ্গে F বিন্দুতে মিলিত হয়৷ AC বাহুর দৈর্ঘ্য 8 সেমি হলে, CF বাহুর দৈর্ঘ্য কত তা লিখি৷

সমাধানঃ

Koshe Dekhi 9 Class 9

E, AC বাহুর মধ্যবিন্দু

∴ EC = ½ AC = ½ × 8 সেমি. = 4 সেমি.

BEC ত্রিভুজের D, BC বাহুর মধ্যবিন্দু এবং BE || DF

∴ F, EC বাহুর মধ্যবিন্দু

∴ CF = ½ EC= ½ × 4 সেমি. = 2 সেমি.

উত্তরঃ CF বাহুর দৈর্ঘ্য 2 সেমি.

Q16. সংক্ষিপ্ত প্রশ্নঃ

(ii) ABC ত্রিভুজের BC, CA এবং AB বাহুর মধ্যবিন্দু যথাক্রমে P, Q, R; যদি AC = 21 সেমি., BC = 29 সেমি. এবং AB = 30 সেমি. হয়, তাহলে ARPQ চতুর্ভুজের পরিসীমা লিখি৷

সমাধানঃ

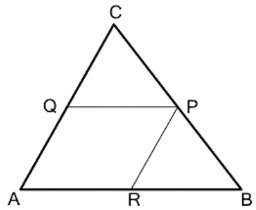
Koshe Dekhi 9 Class 9

Q, AC বাহুর মধ্যবিন্দু

∴ QA = ½ AC = ½ × 21 সেমি. = 10.5 সেমি.

R, AB বাহুর মধ্যবিন্দু

∴ AR = ½ AB = ½ × 30 সেমি. = 15 সেমি.

Q, AC বাহুর মধ্যবিন্দু এবং P, BC বাহুর মধ্যবিন্দু

∴ PQ = ½ AB = ½ × 30 সেমি. = 15 সেমি.

আবার, R, AB বাহুর মধ্যবিন্দু এবং P, BC বাহুর মধ্যবিন্দু

∴ RP = = ½ AC = ½ × 21 সেমি. = 10.5 সেমি.

ARPQ চতুর্ভুজের পরিসীমা

= AR + RP + PQ + AQ

= (15 + 10.5 + 15 + 10.5) সেমি.

= 51 সেমি.

উত্তরঃ ARPQ চতুর্ভুজের পরিসীমা 51 সেমি.

Q16. সংক্ষিপ্ত প্রশ্নঃ

(iii) ABC ত্রিভুজের AC বাহুর উপর D যে-কোনো একটি বিন্দু৷ P, Q, X, Y যথাক্রমে AB, BC, AD এবং DC এর মধ্যবিন্দু। PX = 5 সেমি. হলে, QY -এর দৈর্ঘ্য কত তা লিখি৷

সমাধানঃ

Koshe Dekhi 9 Class 9

ABD ত্রিভুজের P, AB বাহুর মধ্যবিন্দু এবং X, AD বাহুর মধ্যবিন্দু

∴ PX =½ BD

বা, BD = 2PX = 2 × 5 সেমি.

∴ BD = 10 সেমি.

BCD ত্রিভুজের Q, BC বাহুর মধ্যবিন্দু এবং Y, CD বাহুর মধ্যবিন্দু

∴ QY =½ BD = ½ × 10 সেমি. = 5 সেমি

উত্তরঃ QY -এর দৈর্ঘ্য 5 সেমি

Q16. সংক্ষিপ্ত প্রশ্নঃ

(iv) ABC ত্রিভুজের BE ও CF মধ্যমা G বিন্দুতে ছেদ করে৷ P এবং Q যথাক্রমে BG এবং CG -এর মধ্যবিন্দু৷ PQ = 3 সেমি. হলে, BC এর দৈর্ঘ্য কত তা লিখি৷

সমাধানঃ

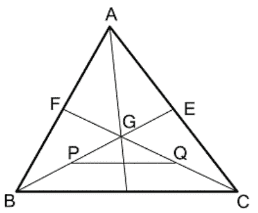
Koshe Dekhi 9 Class 9

BGC ত্রিভুজের P, BG বাহুর মধ্যবিন্দু এবং Q, CG বাহুর মধ্যবিন্দু

∴ PQ = ½ BC

বা, BC = 2PQ

বা, BC = 2 × 3 সেমি

∴ BC = 6 সেমি.

উত্তরঃ BC এর দৈর্ঘ্য 6 সেমি.

Q16. সংক্ষিপ্ত প্রশ্নঃ

(v) ABC ত্রিভুজের BC, CA ও AB বাহুর মধ্যবিন্দু যথাক্রমে D, E ও F; FE, AD -কে O বিন্দুতে ছেদ করে৷ AD = 6 সেমি. হলে, AO এর দৈর্ঘ্য কত তা লিখি৷

সমাধানঃ

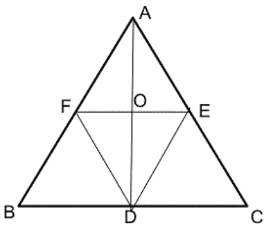
Koshe Dekhi 9 Class 9

ABC ত্রিভুজের D, BC বাহুর মধ্যবিন্দু এবং F, AB বাহুর মধ্যবিন্দু

∴ FD || AC

সুতরাং, FD || AE

আবার, ABC ত্রিভুজের E, AC বাহুর মধ্যবিন্দু এবং F, AB বাহুর মধ্যবিন্দু

∴ ED || AB

সুতরাং, ED || AF

AEDF চতুর্ভুজের FD || AE এবং ED || AF

∴ AEDF একটি সামান্তরিক

যেহেতু সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে

∴ AO = ½ AD = ½ × 6 সেমি.

= 3 সেমি.

উত্তরঃ AO এর দৈর্ঘ্য ও সেমি.

Koshe Dekhi 9 Class 9

Koshe Dekhi 9 Class 9,Koshe Dekhi 9 Class 9,Koshe Dekhi 9 Class 9,Koshe Dekhi 9 Class 9,Koshe Dekhi 9 Class 9,Koshe Dekhi 9 Class 9,Koshe Dekhi 9 Class 9,

Koshe Dekhi 9 Class 9,Koshe Dekhi 9 Class 9,Koshe Dekhi 9 Class 9,Koshe Dekhi 9 Class 9,Koshe Dekhi 9 Class 9,Koshe Dekhi 9 Class 9,Koshe Dekhi 9 Class 9,Koshe Dekhi 9 Class 9, Koshe Dekhi 9 Class 9, Koshe Dekhi 9 Class 9, Koshe Dekhi 9 Class 9, Koshe Dekhi 9 Class 9

Koshe Dekhi 9 Class 9, Koshe Dekhi 9 Class 9, Koshe Dekhi 9 Class 9, Koshe Dekhi 9 Class 9, Koshe Dekhi 9 Class 9, Koshe Dekhi 9 Class 9, Koshe Dekhi 9 Class 9, Koshe Dekhi 9 Class 9