 |
| Fig.1 |
Let ABC is a triangle whose three angles are ∠A = x°, ∠B = y° and ∠C = z°
We have to prove x° + y° + z° = 180°
Construction :
Three sides AB, BC, and AC are extended in both the directions. Then a line RAS is drawn from point A in such a way that RAS॥PQ.
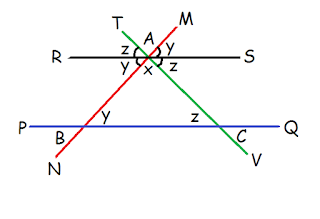 |
| Fig.2 |
Proof: ∵ RAS॥PQ and MN is transversal ( According to the construction )
∴ ∠CBA = ∠NAS = y°
Similarly, ∠BCA = ∠TAR = z°
Now, at point A, ∠SAC = ∠TAR = z° ( vertical opposite angles ) and
∠RAB = ∠NAS = y° ( vertical opposite angles )
Now, At the point A, ∠RAS = 180° ( straight angle )
⇒ ∠RAB + ∠BAC + ∠SAC = 180°
⇒ y° + x° + z° = 180°
∴ x° + y° + z° = 180° (Proved)
For more details click on the video below.