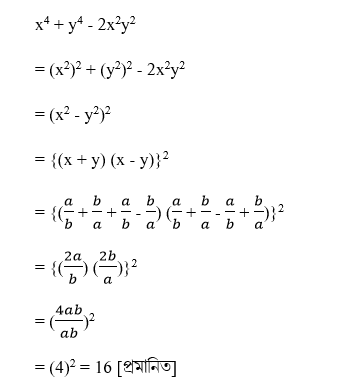Koshe Dekhi 12.3 Class 7

1. (a² − b²) = (a + b) (a − b) এই সূত্রের সাহায্যে মান নির্ণয় করি।

(i) (37)² −(13)²

সমাধানঃ

(37)² −(13)²

= (37 + 13) (37 − 13)

= 50 × 24

= 1200

(ii) (2.06)² − (0.94)²

সমাধানঃ

(2.06)² − (0.94)²

= (2.06 + 0.94) (2.06 − 0.94)

= 3 × 1.12

= 3.36

(iii) (78) × (82)

সমাধানঃ

(78) × (82)

= (80 − 2) (80 + 2)

= (80)² − (2)²

= 6400 − 4

= 6396

(iv) 1.15 × 0.85

সমাধানঃ

1.15 × 0.85

= (1.00 + 0.15) (1.00 − 0.15)

= (1)² − (0.15)²

= 1 − 0.0225

= 0.9775

উত্তরঃ

(v) (65)² − (35)²

সমাধানঃ

(65)² − (35)²

= (65 + 35) (65 − 35)

= 100 × 30

= 3000

2. (i) k − p² = (9+p) (9-p) হলে k -এর মান কত হবে বের করি।

সমাধানঃ

k − p² = (9+p) (9-p)

বা, k − p² = 81 − p²

∴ k = 81

উত্তরঃ k -এর মান 81

(ii) (25 − 4x²) = (5 + ax) (5− ax) হলে a -এর ধনাত্মক মান কত হবে হিসাব করি।

সমাধানঃ

(25 − 4x²) = (5 + ax) (5− ax)

বা, (25 − 4x²) = 25 − a²x²

বা, − 4x²= − a²x²

বা, $a^{2}=\frac{-4x^{2}}{-x^{2}}$

বা, a² = 4

∴ a = ± 2

উত্তরঃ a -এর ধনাত্মক মান 2

(iii) (4 − x) × ____ = (16 − x²) হলে ফাঁকা ঘরে কি হবে লিখি।

সমাধানঃ

(4 − x) × ____ = (16 − x²)

বা, (4 − x) × p (ধরি) = (4 − x) (4 + x)

∴ p = (4 + x)

3. সূত্রের সাহায্যে গুণফলরূপে প্রকাশ করি।

(i) 25l² − 16m²

সমাধানঃ

25l² − 16m²

= (5l)² − (4m)²

= (5l + 4m) (5l − 4m)

(ii) 49x⁴ − 36y⁴

সমাধানঃ

49x⁴ − 36y⁴

= (7x²)² − (6y²)²

= (7x²+ 6y²) (7x²− 6y²)

(iii) (2a + b)²− (a + b)²

সমাধানঃ

(2a + b)²− (a + b)²

= [(2a + b) + (a + b)] [(2a + b) − (a + b)]

= [2a + b + a + b] [2a + b − a − b]

= (3a + 2b) a

(iv) (x + y)² − (a + b)²

সমাধানঃ

(x + y)² − (a + b)²

= [(x + y) + (a + b)] [(x + y) − (a + b)]

= [x + y + a + b] [x + y − a − b]

(v) (x + y − z)² − (x − y + z)²

সমাধানঃ

(x + y − z)² − (x − y + z)²

= [(x + y − z) + (x − y + z)] [(x + y − z) − (x − y + z)]

= [x + y − z + x − y + z] [x + y − z − x + y − z]

= 2x (2y − 2z)

(vi) (m + p + q)² − (m − p − q)²

সমাধানঃ

(m + p + q)² − (m − p − q)²

= [(m + p + q) + (m − p − q)] [(m + p + q) − (m − p − q)]

= [m + p + q + m − p − q] [m + p + q − m + p + q]

= 2m (2p + 2q)

4. সূত্রের সাহায্যে ক্রমিক গুণফল নির্ণয় করি।

(i) (c + d) (c − d) (c² + d²)

সমাধানঃ

(c + d) (c − d) (c² + d²)

= (c² − d²) (c² + d²)

= (c⁴ − d⁴)

(ii) (1 − 3x²) (1 + 3x²) (1 + 9x⁴)

সমাধানঃ

(1 − 3x²) (1 + 3x²) (1 + 9x⁴)

= (1 − 9x⁴) (1 + 9x⁴)

= (1 − 81x⁸)

(iii) (a²+ b²) (a² − b²) (a⁴ + b⁴) (a⁸ + b⁸)

সমাধানঃ

(a²+ b²) (a² − b²) (a⁴ + b⁴) (a⁸ + b⁸)

= (a⁴ − b⁴) (a⁴ + b⁴) (a⁸ + b⁸)

= (a⁸ − b⁸) (a⁸ + b⁸)

= (a¹⁶ − b¹⁶)

5. নিচের বীজগাণিতিক সংখ্যামালাগুলি গুণফলরূপে প্রকাশ করি।

(i) 16c⁴ − 81d⁴

সমাধানঃ

16c⁴ − 81d⁴

= (4c²)² − (9d²)²

= (4c² + 9d²) (4c² − 9d²)

= (4c² + 9d²) [( 2c)² − (3d)²]

= (4c² + 9d²) ( 2c + 3d) ( 2c − 3d)

(ii) p⁴ q⁴ − r⁴s⁴

সমাধানঃ

p⁴ q⁴ − r⁴s⁴

= (p²q²)² − (r²s²)²

= (p²q²+ r²s² ) (p²q²− r²s² )

= (p²q²+ r²s² ) [(pq)²− (rs)²]

= (p²q²+ r²s² ) [(pq + rs) (pq− rs)]

= (pq + rs) (pq− rs) (p²q²+ r²s² )

(iii) 81 − x⁴

সমাধানঃ

81 − x⁴

= (9)² − (x²)²

= (9 + x²) (9 − x²)

= (9 + x²) (3² − x²)

= (9 + x²) ( 3 + x) (3 − x)

= ( 3 + x) (3 − x) (9 + x²)

(iv) 625 − a⁴b⁴

সমাধানঃ

625 − a⁴b⁴

= (25)² − (a²b²)²

= (25 + a²b²) (25 − a²b²)

= (25 + a²b²) [(5)² − (ab)²]

= (25 + a²b²) [(5 + ab) (5 − ab)]

= (5 + ab) (5 − ab) (25 + a²b²)

6. (p+q)⁴− (p − q)⁴ = 8pq (p² + q²) – প্রমাণ করি।

সমাধানঃ

(p+q)⁴− (p − q)⁴

= [(p+q)²]² − [(p − q)²]²

= [(p+q)²+ (p − q)²] [(p+q)²−(p − q)²]

= 2(p² + q²) × 4pq

= 8pq (p² + q²)

7. সূত্রের সাহায্যে গুণ করি : (a + b + c) (b + c − a) (c + a − b) (a + b − c)

সমাধানঃ

Koshe Dekhi 12.3 Class 7

8. ${\color{Blue} x=\frac{a}{b}+\frac{b}{a}}$ ${\color{Blue} y=\frac{a}{b}-\frac{b}{a}}$ হলে দেখাই যে, x⁴ + y⁴− 2x² y² = 16

সমাধানঃ

Koshe Dekhi 12.3 Class 7

9. সূত্রের সাহায্যে গুণ করি (a²+ a + l) (a² − a + 1) (a⁴ − a²+ 1)

সমাধানঃ

Koshe Dekhi 12.3 Class 7

উত্তরঃ

10. যদি $x=\left ( a+\frac{1}{a} \right )$ এবং ${\color{Blue} y=\left ( a-\frac{1}{a} \right )}$ হয়, তাহলে x⁴ + y⁴− 2x² y² -এর মান সূত্রের সাহায্যে বের করি।

সমাধানঃ

Koshe Dekhi 12.3 Class 7

11. (4x²+ 4x + 1 − a²+ 8a − 16) -কে দুটি বর্গের অন্তররূপে (a² − b²আকারে) প্রকাশ করি।

সমাধানঃ

(4x²+ 4x + 1 − a²+ 8a − 16)

= [ (2x)² + 2 × 2x × 1+ 1²] − [(a)² − 2 × a × 4 + (4)²]

= (2x + 1)² − ( a − 4)²

12. ${\color{Blue} a^{2}+\frac{1}{a^{2}}-3}$ কে দুটি বর্গের অন্তররূপে (a² − b² আকারে) প্রকাশ করি।

সমাধানঃ

$a^{2}+\frac{1}{a^{2}}-3$

$=a^{2}+\frac{1}{a^{2}}-2-1$

$=\left (a \right )^{2}+\left (\frac{1}{a} \right )^{2}-2\times a\times \frac{1}{a}-1$

$=\left ( a-\frac{1}{a} \right )^{2}-1$

$=\left ( a-\frac{1}{a} \right )^{2}-1^{2}$

= $=\left ( a-\frac{1}{a}+1 \right )\left ( a-\frac{1}{a}-1 \right )$