Koshe dekhi 16 class 9

1. নীচের ছবিগুলির পরিসীমা হিসাব করে লিখি –

(i)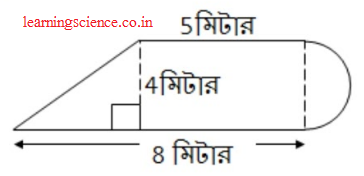

সমাধানঃ

প্রদত্ত চিত্রে,

EF = BC = 5 মিটার,

AC = 8 মিটার

∴ AB = (8 − 5) মিটার = 3 মিটার

BF = CE = 4 মিটার

∴ CDE অর্ধবৃত্তের ব্যাসার্ধ

$r=\frac{CE}{2}$

বা, $r=\frac{4}{2}$

∴ r = 2 মিটার

∴ CDE অর্ধবৃত্তের পরিধি

$=\pi r$

$=\frac{22}{7}\times 2$

$=\frac{44}{7}$

$=6\frac{2}{7}$ মিটার

ΔABF একটি সমকোণী ত্রিভুজ যার ∠B = 90°,

লম্ব (BF) = 4 মিটার

ভূমি (AB) = 3 মিটার

অতিভুজ (AF) = x মিটার (ধরি)

আমরা জানি, সমকোণী ত্রিভুজের ক্ষেত্রে,

( অতিভুজ )² = ( লম্ব )² + ( ভূমি )²

$\left ( x \right )^{2}=\left ( 4 \right )^{2}+\left ( 3 \right )^{2}$

$x^{2}=16+9$

$x^{2}=25$

$x=\pm \sqrt{25}$

∴ x = ± 5

যেহেতু, ত্রিভুজের বাহুর দৈর্ঘ্য ঋণাত্মক হতে পারে না তাই x ≠ − 5

∴ x = + 5 মিটার

∴ প্রদত্ত চিত্রের পরিসীমা

= AC বাহুর দৈর্ঘ্য + CDE অর্ধবৃত্তের পরিধি + EF বাহুর দৈর্ঘ্য + AF বাহুর দৈর্ঘ্য

$=\left (8+6\frac{2}{7}+5+5 \right )$ মিটার

$=\left (18+6+\frac{2}{7} \right )$ মিটার

$=\left (24+\frac{2}{7} \right )$ মিটার

$=24\frac{2}{7}$ মিটার

উত্তরঃ প্রদত্ত চিত্রের পরিসীমা ${\color{DarkGreen} 24\frac{2}{7}}$ মিটার।

1. নীচের ছবিগুলির পরিসীমা হিসাব করে লিখি –

(ii)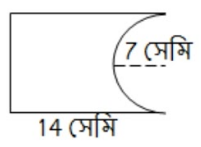

সমাধানঃ

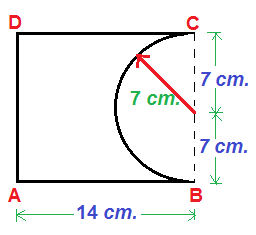
প্রদত্ত চিত্রে,

AB = CD = 14 সেমি

অর্ধবৃত্তের ব্যাসার্ধ (r) = 7 সেমি

∴ অর্ধবৃত্তের ব্যাস (BC) = 2r = 2 × 7 = 14 সেমি

∴ AD

= BC

= 14 সেমি

∴ অর্ধবৃত্তের পরিধি

$=\pi r$

$=\frac{22}{7}\times 7$ সেমি

= 22 সেমি

∴ প্রদত্ত চিত্রের পরিসীমা

= AB বাহুর দৈর্ঘ্য + অর্ধবৃত্তের পরিধি + CD বাহুর দৈর্ঘ্য + AD বাহুর দৈর্ঘ্য

= 14 সেমি + 22 সেমি + 14 সেমি + 14 সেমি

= 64 সেমি

উত্তরঃ প্রদত্ত চিত্রের পরিসীমা 64 সেমি।

2. 35 মিটার দৈর্ঘ্যের ব্যাসার্ধবিশিষ্ট একটি বৃত্তাকার তারের রিং তৈরি করতে কত লম্বা তার নেব হিসাব করে লিখি।

সমাধানঃ

প্রদত্ত,

বৃত্তাকার তারের রিং -এর ব্যাসার্ধ (r) = 35 মিটার

∴ রিংটির পরিধি

$=2\pi r$

$=2\times \frac{22}{7}\times 35$

= 220 মিটার

উত্তরঃ তারটি 220 মিটার লম্বা নিতে হবে।

3. একটি ট্রেনের চাকার ব্যাসার্ধের দৈর্ঘ্য 0.35 মিটার। 1 মিনিটে চাকাটি 450 বার ঘুরলে ট্রেনটির গতিবেগ ঘণ্টায় কত কিমি হিসাব করে লিখি।

সমাধানঃ

প্রদত্ত,

ট্রেনটির চাকার ব্যাসার্ধ (r) = 0.35 মিটার

∴ চাকার পরিধি

$=2\pi r$

$=2\times \frac{22}{7}\times 0.35$

$=2\times \frac{22}{7}\times \frac{35}{100}$

$=\frac{22}{10}$

= 2.2 মিটার

1 মিনিটে চাকাটি 450 বার ঘুরলে, ট্রেনটি 1 মিনিটে অতিক্রম করে

= 450 × 2.2 মিটার

= 990 মিটার

∴ 60 মিনিটে [ যেহেতু, 60 মিনিট = 1 ঘণ্টা ] ট্রেনটি অতিক্রম করে

= (990 × 60) মিটার

= 59400 মিটার

$=\frac{59400}{1000}$ কিমি

= 59.4 কিমি

উত্তরঃ ট্রেনটির গতিবেগ ঘণ্টায় 59.4 কিমি।

4. আমােদপুর গ্রামের একটি বৃত্তাকার মাঠের ব্যাসার্ধের দৈর্ঘ্য 280 মিটার। চৈতালি প্রতি ঘণ্টায় 5.5 কিমি. বেগে হেঁটে মাঠটি পরিক্রমা করতে চায়। হিসাব করে দেখি মাঠটি একবার প্রদক্ষিণ করতে চৈতালির কত সময় লাগবে ?

সমাধানঃ

প্রদত্ত,

বৃত্তাকার মাঠের ব্যাসার্ধ (r) = 280 মিটার

∴ মাঠটির পরিধি

$=2\pi r$

$=2\times \frac{22}{7}\times 280$

= 1760 মিটার

5.5 কিমি.

= 5.5 × 1000 মিটার

= 5500 মিটার

এবং

1 ঘন্টা = 60 মিনিট

চৈতালি, 5500 মিটার অতিক্রম করে 60 মিনিটে

1 মিটার অতিক্রম করে $=\frac{60}{5500}$ মিনিটে

∴ 1760 মিটার অতিক্রম করে

$=\frac{60\times 1760}{5500}$ মিনিটে

$=\frac{96}{5}$ মিনিটে

$=19\frac{1}{5}$ মিনিটে

= 19 মিনিট + $\frac{1}{5}$ মিনিট

= 19 মিনিট + $\frac{1}{5}\times 60$ সেকেন্ড [1 মিনিট = 60 সেকেন্ড ]

= 19 মিনিট 12 সেকেন্ড

উত্তরঃ মাঠটি একবার প্রদক্ষিণ করতে চৈতালির 19 মিনিট 12 সেকেন্ড সময় লাগবে।

5. তথাগত একটি তামার তার আয়তাকারে বেঁকিয়েছে যার দৈর্ঘ্য 18 সেমি. এবং প্রস্থ 15 সেমি.। আমি এই তামার তারটি বেঁকিয়ে বৃত্ত তৈরি করলাম৷ হিসাব করে এই বৃত্তাকার তামার তারটির ব্যাসার্ধের দৈর্ঘ্য লিখি।

সমাধানঃ

আয়তাকার তারের পরিসীমা

= 2 × (দৈর্ঘ্য + প্রস্থ )

= 2 × (18 + 15) সেমি.

= 2 × 33 সেমি.

= 66 সেমি.

= বৃত্তাকার তারের পরিধি

ধরি,

বৃত্তাকার তামার তারটির ব্যাসার্ধের দৈর্ঘ্য r সেমি.।

প্রশ্নানুসারে,

$2\pi r=66$

বা, $2\times \frac{22}{7}\times r=66$

বা, $r=\frac{66\times 7}{2\times 22}$

বা, $r=\frac{21}{2}$

∴ r = 10.5

উত্তরঃ বৃত্তাকার তামার তারটির ব্যাসার্ধের দৈর্ঘ্য 10.5 সেমি.।

6. একটি অর্ধবৃত্তাকার মাঠের পরিসীমা 108 মিটার হলে মাঠের ব্যাসের দৈর্ঘ্য হিসাব করে লিখি।

সমাধানঃ

ধরি,

অর্ধবৃত্তাকার মাঠের ব্যাসার্ধ = r মিটার

আমরা জানি,

অর্ধবৃত্তাকার মাঠের পরিসীমা $=\pi r+2r$ মিটার

প্রশ্নানুসারে,

$\pi r+2r=108$

বা, $\frac{22}{7}\times r+2r=108$

বা, $r\left (\frac{22}{7}+2 \right )=108$

বা, $r\left (\frac{22+14}{7}\right )=108$

বা, $r\times \frac{36}{7}=108$

বা, $r=\frac{108\times 7}{36}$

∴ r = 21

∴ মাঠটির ব্যাসের দৈর্ঘ্য

= 2r

= 2 × 21 মিটার

= 42 মিটার

উত্তরঃ অর্ধবৃত্তাকার মাঠের ব্যাসের দৈর্ঘ্য 42 মিটার।

7. একটি চাকার পরিধি ও ব্যাসের দৈর্ঘ্যের অন্তর 75 সেমি. হলে, ওই চাকার ব্যাসার্ধের দৈর্ঘ্য হিসাব করে লিখি।

সমাধানঃ

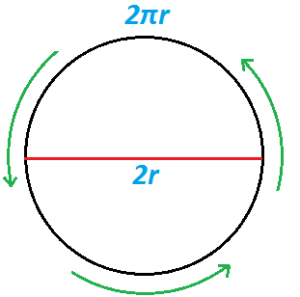
ধরি,

চাকাটির ব্যাসার্ধ = r সেমি.

প্রশ্নানুসারে,

চাকার পরিধি − ব্যাসের দৈর্ঘ্য = 75 সেমি.

বা, $2\pi r-2r=75$

বা, $r\left ( 2\times \frac{22}{7}-2 \right )=75$

বা, $r\left (\frac{44}{7}-2 \right )=75$

বা, $r\left (\frac{44-14}{7} \right )=75$

বা, $r\times \frac{30}{7}=75$

বা, $r=75\times \frac{7}{30}$

বা, $r=\frac{35}{2}$

∴ r = 17.5

উত্তরঃ চাকাটির ব্যাসার্ধের দৈর্ঘ্য 17.5 সেমি.

8. 28 মিটার দৈর্ঘ্যের ব্যাসবিশিষ্ট বৃত্তাকার ট্র্যাকে পূজা ও জাকির একই জায়গা থেকে একই সময়ে প্রতিযােগিতা শুরু করে। পূজা যখন 4 পাক ঘুরে প্রতিযােগিতা শেষ করে জাকির তখন একপাক পিছনে থাকে। প্রতিযােগিতাটি কত মিটারের ছিল এবং পূজা জাকিরকে কত মিটারে পরাজিত করেছে হিসাব করে লিখি।

সমাধানঃ

প্রদত্ত, বৃত্তাকার ট্র্যাকের ব্যাস = 28 মিটার

∴ ট্র্যাকটির ব্যাসার্ধ $\left ( r \right )=\frac{28}{2}=14$ মিটার

∴ ট্র্যাকটির পরিধি

$=2\pi r$

$=2\times \frac{22}{7}\times 14$

= 88 মিটার

অর্থাৎ, ট্র্যাকটির 1 পাক ঘুরে আসলে হয় 88 মিটার।

যেহেতু, পূজা 4 পাক ঘুরে প্রতিযােগিতা শেষ করে,

সুতরাং, প্রতিযােগিতাটি ছিল

= 88 মিটার × 4 পাক

= 352 মিটারের

আবার, পূজা যখন প্রতিযােগিতা শেষ করে জাকির তখন একপাক পিছনে থাকে।

অর্থাৎ, জাকির পূজার থেকে 88 মিটার পিছনে ছিল।

উত্তরঃ প্রতিযােগিতাটি 352 মিটারের ছিল এবং পূজা জাকিরকে 88 মিটারে পরাজিত করেছে।

9. আমাদের পাড়ার একটি পাতকুয়াের পরিধি 440 সেমি.। এই পাতকুয়াের চারধারে সমান চওড়া একটি পাথরের পাড় আছে৷ যদি বেধসমেত পাতকুয়াের পরিধি 616 সেমি. হয় তবে পাথরের পাড় কত চওড়া হিসাব করে লিখি।

সমাধানঃ

ধরি, পাতকুয়াের পাড়ের ভিতরের দিকের ব্যাসার্ধ r সেমি এবং বাইরের দিকের ব্যাসার্ধ R সেমি।

∴ পাথরের পাড়টি চওড়া = (R − r) সেমি।

প্রদত্ত,

পাতকুয়াের পরিধি (2πr) = 440 সেমি.।

বেধসমেত পাতকুয়াের পরিধি (2πR) = 616 সেমি.

প্রশ্নানুসারে,

$2\pi R-2\pi r=616-440$

বা, $2\pi \left ( R-r \right )=176$

বা, $\left ( R-r \right )=\frac{176}{2\pi }$

বা, $\left ( R-r \right )=\frac{176}{2\times \frac{22}{7}}$

বা, $\left ( R-r \right )=\frac{176\times 7}{2\times 22}$

∴ (R − r) = 28

উত্তরঃ পাথরের পাড় 28 সেমি চওড়া।

10. গ্রামের নিয়ামতচাচা একটি মােটরের চাকার সঙ্গে বেল্ট দিয়ে একটি মেশিনের চাকা যুক্ত করেছেন। মােটরের চাকার ব্যাসের দৈর্ঘ্য 14 সেমি. এবং মেশিনের চাকার ব্যাসের দৈর্ঘ্য 94.5 সেমি.। মােটরের চাকা যদি প্রতি সেকেন্ডে 27 বার ঘােরে, তবে মেশিনের চাকা ঘণ্টায় কতবার ঘুরবে হিসাব করে লিখি।

সমাধানঃ

প্রদত্ত, মােটরের চাকার ব্যাসের দৈর্ঘ্য 14 সেমি.

∴ মােটরের চাকার ব্যাসার্ধ $\left ( r \right )=\frac{14}{2}=7$ সেমি.

ও পরিধি

$=2\pi r$

$=2\times \frac{22}{7}\times 7$

= 44 সেমি.

প্রদত্ত, মেশিনের চাকার ব্যাসের দৈর্ঘ্য 94.5 সেমি.

∴ মেশিনের চাকার ব্যাসার্ধ $\left ( R \right )=\frac{94.5}{2}$ সেমি.

ও পরিধি

$=2\pi r$

$=2\times \frac{22}{7}\times \frac{94.5}{2}$

$=2\times \frac{22}{7}\times \frac{945}{2\times 10}$

= 297 সেমি.

যেহেতু, মােটরের চাকা প্রতি সেকেন্ডে 27 বার ঘােরে,

∴ চাকাটি প্রতি সেকেন্ডে অতিক্রম করে

= 27 × 44 সেমি.

= 1188 সেমি.

এখন, 1188 সেমি. পথ যেতে মেশিনের চাকা 1 সেকেন্ডে ঘােরে

$=\frac{1188}{297}$ বার

= 4 বার

∴ 1 ঘন্টা অর্থাৎ, 3600 সেকেন্ডে ঘােরে

= 4 × 3600

= 14400 বার

উত্তরঃ মেশিনের চাকা ঘণ্টায় 14400 বার ঘুরবে।

11. আমাদের ক্লাব ঘরের ঘড়িটির ঘণ্টার কাঁটা ও মিনিটের কাঁটার দৈর্ঘ্য যথাক্রমে 8.4 সেমি. ও 14 সেমি.। একদিনে প্রতিটি কাঁটা কতটা পথ অতিক্রম করবে হিসাব করে লিখি।

সমাধানঃ

ঘড়িটির ঘণ্টার কাঁটার পরিধি

$=2\pi r$

$=2\times \frac{22}{7}\times 8.4$

= 52.8 সেমি.

ঘণ্টার কাঁটা 12 ঘন্টায় 1 বার পরিক্রমা করে।

সুতরাং,

একদিনে অর্থাৎ, 24 ঘন্টায় কাঁটাটি 2 বার সমগ্র ঘড়িটি অতিক্রম করে।

∴ একদিনে ঘন্টার কাঁটা মোট পথ অতিক্রম করে

= 2 × 52.8 সেমি.

= 105.6 সেমি.

ঘড়িটির মিনিটের কাঁটার পরিধি

$=2\pi R$

$=2\times \frac{22}{7}\times 14$

= 88 সেমি.

মিনিটের কাঁটা 1 ঘন্টায় 1 বার পরিক্রমা করে।

সুতরাং,

একদিনে অর্থাৎ, 24 ঘন্টায় কাঁটাটি 24 বার সমগ্র ঘড়িটি অতিক্রম করে।

∴ একদিনে মিনিটের কাঁটা মোট পথ অতিক্রম করে

= 24 × 88 সেমি.

= 2112 সেমি.

উত্তরঃ একদিনে ঘন্টার কাঁটা মোট 105.6 সেমি. পথ অতিক্রম করে এবং মিনিটের কাঁটা মোট 2112 সেমি.পথ অতিক্রম করে।

12. আমি ও বন্ধু মিহির দুটি বৃত্ত এঁকেছি যাদের ব্যাসের দৈর্ঘ্যের অনুপাত $\dpi{100} \small {\color{Blue} \square :\square }$ হিসাব করে দেখছি আমাদের বৃত্তের পরিধির অনুপাত হয় $\dpi{100} \small {\color{Blue} \square :\square }$

সমাধানঃ

ধরি, আমি ও বন্ধু মিহির দুটি বৃত্ত এঁকেছি যাদের ব্যাসের দৈর্ঘ্যের অনুপাত a : b

অর্থাৎ, আমার আঁকা বৃত্তের ব্যাসের দৈর্ঘ্য ax সেমি ও মিহিরের আঁকা বৃত্তের ব্যাসের দৈর্ঘ্য bx সেমি।

∴ আমার আঁকা বৃত্তের ব্যাসার্ধ $=\frac{ax}{2}$ সেমি

ও মিহিরের আঁকা বৃত্তের ব্যাসার্ধ $=\frac{bx}{2}$ সেমি

∴ আমার ও মিহিরের আঁকা বৃত্তের পরিধির অনুপাত

$=2\pi \times \frac{ax}{2}:2\pi \times \frac{bx}{2}$

= a : b

উত্তরঃ আমার ও মিহিরের আঁকা বৃত্তের পরিধির অনুপাত a : b

13. রহিমের একটি বৃত্তাকার মাঠের পুরোটা একবার দৌড়াতে যে সময় লাগে ব্যাস বরাবর একপ্রান্ত থেকে আর একপ্রান্তে যেতে 40 সেকেন্ড কম সময়। লাগে। রহিমের গতিবেগ 90 মিটার প্রতি মিনিট হলে, মাঠের ব্যাসের দৈর্ঘ্য হিসাব করে লিখি।

সমাধানঃ

ধরি, বৃত্তাকার মাঠের ব্যাসার্ধ r মিটার।

∴ ব্যাস = 2r মিটার।

রহিম, 1 মিনিট অর্থাৎ, 60 সেকেন্ডে যায় 90 মিটার

1 সেকেন্ডে যায় $=\frac{90}{60}$ মিটার

∴ 40 সেকেন্ডে যায়

$=\frac{90}{60}\times 40$ মিটার

= 60 মিটার

∴ মাঠের পরিধি থেকে মাঠটির ব্যাস 60 মিটার কম।

সুতরাং,

মাঠের পরিধি − মাঠের ব্যাস = 60

বা, $2\pi r-2r=60$

বা, $2r\left ( \frac{22}{7}-1 \right )=60 {\color{Blue} \left [ \because \pi =\frac{22}{7} \right ]}$

বা, $2r\left ( \frac{22-7}{7} \right )=60$

বা, $2r\times \frac{15}{7}=60$

বা, $2r=\frac{60\times 7}{15}$

∴ 2r = 28

উত্তরঃ বৃত্তাকার মাঠের ব্যাসের দৈর্ঘ্য 28 মিটার।

14. দুটি বৃত্তের পরিধির অনুপাত 2 : 3 এবং তাদের ব্যাসার্ধের দৈর্ঘ্যের অন্তর 2 সেমি। বৃত্ত দুটির ব্যাসের দৈর্ঘ্য হিসাব করে লিখি।

সমাধানঃ

ধরি, ছোট বৃত্তের ব্যাসার্ধের দৈর্ঘ্য r সেমি এবং বড় বৃত্তের ব্যাসার্ধের দৈর্ঘ্য (r + 2) সেমি।

∴ ছোট বৃত্তের পরিধি $=2\pi r$ সেমি এবং

বড় বৃত্তের পরিধি $=2\pi \left (r+2 \right )$ সেমি

প্রশ্নানুসারে,

$\frac{2\pi r}{2\pi \left (r+2 \right )}=\frac{2}{3}$

বা, $\frac{r}{\left (r+2 \right )}=\frac{2}{3}$

বা, 3r = 2r + 4

বা, 3r − 2r = 4

∴ r = 4

∴ ছোট বৃত্তের ব্যাস

= 2 × ছোট বৃত্তের ব্যাসার্ধ

= 2 × 4

= 8 সেমি

এবং

বড় বৃত্তের ব্যাস

= 2 × বড় বৃত্তের ব্যাসার্ধ

= 2 × (4 + 2)

= 2 × 6

= 12 সেমি

উত্তরঃ বৃত্ত দুটির ব্যাসের দৈর্ঘ্য 8 সেমি এবং 12 সেমি।

15. 196 বর্গ সেমি. ক্ষেত্রফলের একটি বর্গাকার পিতলের পাত থেকে চারটি সর্ববৃহৎ বৃত্তাকার পাত কেটে নেওয়া হলাে। প্রতিটি বৃত্তাকার পাতের পরিধি হিসাব করে লিখি।

সমাধানঃ

প্রদত্ত, বর্গক্ষেত্রের ক্ষেত্রফল 196 বর্গ সেমি.

∴ বর্গক্ষেত্রটির বাহুর দৈর্ঘ্য (a)

$=\sqrt{196}$

= 14 সেমি.

ধরি, বৃত্তাকার পাতগুলির প্রত্যেকটির ব্যাসার্ধ r সেমি. ও ব্যাস 2r সেমি.

প্রশ্নানুসারে,

2r + 2r = a

বা, 4r = 14

বা, $r=\frac{14}{4}$

$\therefore r=\frac{7}{2}$

∴ প্রতিটি বৃত্তাকার পাতের পরিধি

$=2\pi r$

$=2\times \frac{22}{7}\times \frac{7}{2}$

= 22 সেমি.

উত্তরঃ প্রতিটি বৃত্তাকার পাতের পরিধি 22 সেমি.।

16. একটি বৃত্তাকার মাঠের বৃত্ত বরাবর একপ্রান্ত থেকে অপরপ্রান্তে যেতে নাসিফার যে সময় লাগে মাঠের ব্যাস বরাবর অতিক্রম করতে তার থেকে 45 সেকেন্ড সময় কম লাগে। নাসিফার গতিবেগ মিনিটে 80 মিটার হলে, মাঠটির ব্যাসের দৈর্ঘ্য হিসাব করে লিখি।

সমাধানঃ

ধরি, বৃত্তাকার মাঠের ব্যাসার্ধ r মিটার।

∴ ব্যাস = 2r মিটার।

নাসিফা, 1 মিনিট অর্থাৎ, 60 সেকেন্ডে যায় 80 মিটার

1 সেকেন্ডে যায় $=\frac{80}{60}$ মিটার

∴ 45 সেকেন্ডে যায়

$=\frac{80}{60}\times 45$ মিটার

= 60 মিটার

∴ মাঠের পরিধি থেকে মাঠটির ব্যাস 60 মিটার কম।

সুতরাং,

মাঠের পরিধি − মাঠের ব্যাস = 60

বা, $2\pi r-2r=60$

বা, $2r\left ( \frac{22}{7}-1 \right )=60 {\color{Blue} \left [ \because \pi =\frac{22}{7} \right ]}$

বা, $2r\left ( \frac{22-7}{7} \right )=60$

বা, $2r\times \frac{15}{7}=60$

বা, $2r=\frac{60\times 7}{15}$

∴ 2r = 28

উত্তরঃ বৃত্তাকার মাঠের ব্যাসের দৈর্ঘ্য 28 মিটার।

17. মহিম সাইকেলে চেপে 7 মিটার 5 ডেসিমি. চওড়া একটি বৃত্তাকার পথের বাইরের ও ভিতরের ধার বরাবর সম্পূর্ণ একবার ঘুরতে যথাক্রমে 46 সেকেন্ড ও 44 সেকেন্ড নেয়। ভিতরের ধার বরাবর বৃত্তটির ব্যাসের দৈর্ঘ্য হিসাব করি।

সমাধানঃ

7 মিটার 5 ডেসিমি.

= (7 × 10) ডেসিমি. + 5 ডেসিমি.

= 75 ডেসিমি.

ধরি, ভিতরের বৃত্তের ব্যাসার্ধ r ডেসিমি.

ও বাইরের বৃত্তের ব্যাসার্ধ (r + 75) ডেসিমি.।

∴ ভিতরের বৃত্তের পরিধি = 2πr ডেসিমি.

ও বাইরের বৃত্তের পরিধি = 2π(r + 75) ডেসিমি.

আমরা জানি,

অতিক্রান্ত দূরত্ব (s) = গতিবেগ (v) × সময় (t)

এখন, গতিবেগ স্থির থাকলে অতিক্রান্ত দূরত্ব সময়ের সাথে সমানুপাতিক হয়।

অর্থাৎ,

$\frac{s_{1}}{s_{2}}=\frac{t_{1}}{t_{2}}$

বা, $\frac{2\pi \left ( r+75 \right )}{2\pi r}=\frac{46}{44}$

বা, $\frac{\left ( r+75 \right )}{r}=\frac{23}{22}$

বা, 23r = 22r + 1650

বা, 23r − 22r = 1650

∴ r = 1650

∴ ভিতরের বৃত্তের ব্যাসের দৈর্ঘ্য

= 2 × ভিতরের বৃত্তের ব্যাসার্ধ

= 2 × 1650

= 3300 ডেসিমি.

$=\frac{3300}{10}$ মিটার

= 330 মিটার

উত্তরঃ ভিতরের বৃত্তের ব্যাসের দৈর্ঘ্য 330 মিটার।

18. একজন সাইকেল আরােহীর একটি বৃত্তাকার পথে বাইরের ও ভিতরের ধার বরাবর সম্পূর্ণ একবার ঘুরতে সময়ের অনুপাত 20 : 19; যদি পথটি 5 মিটার চওড়া হয়, তবে ভিতরের বৃত্তের ব্যাসের দৈর্ঘ্য লিখি।

সমাধানঃ

ধরি, ভিতরের বৃত্তের ব্যাসার্ধ r মিটার ও বাইরের বৃত্তের ব্যাসার্ধ (r + 5) মিটার।

∴ ভিতরের বৃত্তের পরিধি = 2πr মিটার

ও বাইরের বৃত্তের পরিধি = 2π(r + 5) মিটার

আমরা জানি,

অতিক্রান্ত দূরত্ব (s) = গতিবেগ (v) × সময় (t)

এখন, গতিবেগ স্থির থাকলে অতিক্রান্ত দূরত্ব সময়ের সাথে সমানুপাতিক হয়।

অর্থাৎ,

$\frac{s_{1}}{s_{2}}=\frac{t_{1}}{t_{2}}$

বা, $\frac{2\pi \left ( r+5 \right )}{2\pi r}=\frac{20}{19}$

বা, $\frac{\left ( r+5 \right )}{r}=\frac{20}{19}$

বা, 20r = 19r + 95

বা, 20r − 19r = 95

∴ r = 95

∴ ভিতরের বৃত্তের ব্যাসের দৈর্ঘ্য

= 2 × ভিতরের বৃত্তের ব্যাসার্ধ

= 2 × 95

= 190 মিটার

উত্তরঃ ভিতরের বৃত্তের ব্যাসের দৈর্ঘ্য 190 মিটার।

19. বহু বিকল্পীয় প্রশ্নঃ (M.C.Q.)

(i) একটি ঘড়ির ঘণ্টার কাঁটা ও মিনিটের কাটার গতিবেগের অনুপাত

(a) 1 : 12

(b) 12 : 1

(d) 24 : 1

সমাধানঃ

ধরি, ঘড়ির ব্যাসার্ধ r একক

∴ ঘড়িটির পরিধি $=2\pi r$ একক

ঘন্টার কাঁটাটি 12 ঘন্টায় সম্পূর্ণ করে $2\pi r$ একক পথ

∴ 1 ঘন্টায় সম্পূর্ণ করে $=\frac{2\pi r}{12}$ একক পথ

অর্থাৎ, ঘণ্টার কাঁটার গতিবেগ $=\frac{2\pi r}{12}$ একক/ঘন্টা

আবার, মিনিটের কাঁটাটি 1 ঘন্টায় সম্পূর্ণ করে $2\pi r$ একক পথ

অর্থাৎ, মিনিটের কাঁটার গতিবেগ $2\pi r$ একক/ঘন্টা

∴ ঘড়িটির ঘণ্টার কাঁটা ও মিনিটের কাটার গতিবেগের অনুপাত

$=\frac{2\pi r}{12}:2\pi r$

$=\frac{1}{12}:1$

$=\frac{1}{12}\times 12:1\times 12$

= 1 : 12

উত্তরঃ (a)

19. বহু বিকল্পীয় প্রশ্নঃ (M.C.Q.)

(ii) একটি বৃত্তাকার পার্ক সম্পূর্ণ একবার পরিক্রমা করতে সােমার $\dpi{100} \small {\color{Blue} \frac{\pi x}{100}}$ মিনিট সময় লাগে। পার্কটি সােজাসুজি ব্যাস বরাবর অতিক্রম করতে সােমার সময় লাগবে

(a) $\dpi{100} \small {\color{Blue} \frac{x}{200}}$ মিনিট

(b) $\dpi{100} \small {\color{Blue} \frac{x}{100}}$ মিনিট

(d) $\dpi{100} \small {\color{Blue} \frac{\pi}{100}}$ মিনিট

সমাধানঃ

ধরি, বৃত্তাকার পার্কের ব্যাসার্ধ r একক

∴ পার্কটির ব্যাস = 2r একক

এবং পরিধি $=2\pi r$ একক

$2\pi r$ একক পথ যেতে সময় লাগে $\dpi{100} \frac{\pi x}{100}$ মিনিট

1 একক পথ যেতে সময় লাগে $\dpi{100} \frac{\pi x}{100\times 2\pi r}$ মিনিট

∴ 2r একক পথ যেতে সময় লাগে

$\dpi{100} =\frac{\pi x\times 2r}{100\times 2\pi r}$ মিনিট

$\dpi{100} =\frac{x}{100}$ মিনিট

∴ পার্কটি সােজাসুজি ব্যাস বরাবর অতিক্রম করতে সােমার সময় লাগবে $\dpi{100} \frac{x}{100}$ মিনিট।

উত্তরঃ (b)

19. বহু বিকল্পীয় প্রশ্নঃ (M.C.Q.)

(iii) একটি বৃত্ত একটি বর্গক্ষেত্রে অন্তর্লিখিত৷ বর্গক্ষেত্রের বাহুর দৈর্ঘ্য 10 সেমি. হলে বৃত্তের ব্যাসের দৈর্ঘ্য

(a) 10 সেমি.

(b) 5 সেমি.

(d) $\dpi{100} \small {\color{Blue} 10\sqrt{2}}$ সেমি.

সমাধানঃ

প্রদত্ত, বর্গক্ষেত্রের বাহুর দৈর্ঘ্য 10 সেমি.

যেহেতু, বৃত্তটি বর্গক্ষেত্রে অন্তর্লিখিত

সুতরাং বৃত্তের ব্যাস হবে বর্গক্ষেত্রের বাহুর দৈর্ঘ্যের সমান।

∴ বৃত্তটির ব্যাস = 10 সেমি.

উত্তরঃ (a)

19. বহু বিকল্পীয় প্রশ্নঃ (M.C.Q.)

(iv) একটি বৃত্ত একটি বর্গক্ষেত্রে পরিলিখিত৷ বর্গক্ষেত্রের বাহুর দৈর্ঘ্য 5 সেমি. হলে, বৃত্তের ব্যাসের দৈর্ঘ্য

(a) $\dpi{100} \small {\color{Blue} 5\sqrt{2}}$ সেমি.

(b) $\dpi{100} \small {\color{Blue} 10\sqrt{2}}$ সেমি.

(d) 10 সেমি.

সমাধানঃ

প্রদত্ত, বর্গক্ষেত্রের বাহুর দৈর্ঘ্য 5 সেমি.

যেহেতু, বৃত্তটি বর্গক্ষেত্রে পরিলিখিত

সুতরাং বৃত্তের ব্যাস হবে বর্গক্ষেত্রের কর্ণের দৈর্ঘ্যের সমান।

আমরা জানি,

বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য

$=\sqrt{2} \times$ বর্গক্ষেত্রের বাহুর দৈর্ঘ্য

$=\sqrt{2} \times 5$

$=5\sqrt{2}$ সেমি.

∴ বৃত্তটির ব্যাস $=5\sqrt{2}$ সেমি.

উত্তরঃ (a)

19. বহু বিকল্পীয় প্রশ্নঃ (M.C.Q.)

(v) একটি বৃত্তাকার বলয় 5 সেমি. চওড়া। বৃত্তের বহিব্যাসার্ধের দৈর্ঘ্য ও অন্তর্ব্যাসার্ধের দৈর্ঘ্যের অন্তর

(a) 5 সেমি.

(b) 2.5 সেমি.

(d) কোনােটিই নয়।

সমাধানঃ

ধরি, বৃত্তের অন্তর্ব্যাসার্ধের দৈর্ঘ্য r সেমি. ও বহিব্যাসার্ধের দৈর্ঘ্য R সেমি.

প্রদত্ত, বৃত্তাকার বলয় 5 সেমি. চওড়া

∴ বহিব্যাসার্ধের দৈর্ঘ্য (R)

= (r + 5) সেমি.

∴ বৃত্তের বহিব্যাসার্ধের দৈর্ঘ্য ও অন্তর্ব্যাসার্ধের দৈর্ঘ্যের অন্তর

= (r + 5) − r

= 5 সেমি.

উত্তরঃ (a)

20. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ

(i) একটি অর্ধবৃত্তের পরিসীমা 36 সেমি. হলে অর্ধবৃত্তের ব্যাসের দৈর্ঘ্য কত ?

সমাধানঃ

ধরি, অর্ধবৃত্তের ব্যাসার্ধ r সেমি

∴ অর্ধবৃত্তটির পরিসীমা

$=\pi r+2r$ সেমি

প্রশ্নানুসারে,

$\pi r+2r=36$

বা, $r\left (\pi +2 \right )=36$

বা, $r\left (\frac{22}{7} +2 \right )=36$

বা, $r\left (\frac{22+14}{7} \right )=36$

বা, $r\times \frac{36}{7}=36$

বা, $r=36\times \frac{7}{36}$

∴ r = 7

∴ অর্ধবৃত্তের ব্যাসের দৈর্ঘ্য

= 2 × অর্ধবৃত্তের ব্যাসার্ধ

= 2 × 7

= 14 সেমি

উত্তরঃ অর্ধবৃত্তটির ব্যাসের দৈর্ঘ্য 14 সেমি।

20. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ

(ii) একটি ঘড়ির মিনিটের কাঁটার দৈর্ঘ্য 7 সেমি.। 90° কোণ ঘুরতে মিনিটের কাটা কত দৈর্ঘ্য ঘুরবে ?

সমাধানঃ

প্রদত্ত,

ঘড়ির মিনিটের কাঁটার দৈর্ঘ্য 7 সেমি.

অর্থাৎ, ব্যাসার্ধ (r) = 7 সেমি.

∴ ঘড়িটির পরিধি

$=2\pi r$

$=2\times \frac{22}{7}\times 7$

= 44 সেমি.

কাঁটাটি 360° অর্থাৎ ঘড়িটি একবার ঘুরতে মোট পথ অতিক্রম করে 44 সেমি.

1° ঘুরতে মোট পথ অতিক্রম করে $=\frac{44}{360}$ সেমি.

∴ 90° ঘুরতে মোট পথ অতিক্রম করে

$=\frac{44}{360}\times 90$ সেমি.

= 11 সেমি.

উত্তরঃ 90° কোণ ঘুরতে মিনিটের কাটা 11 সেমি. দৈর্ঘ্য ঘুরবে।

20. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ

(iii) কোনাে বর্গক্ষেত্রের অন্তর্বৃত্ত ও পরিবৃত্তের ব্যাসার্ধের অনুপাত কত ?

সমাধানঃ

বর্গক্ষেত্রের অন্তর্বৃত্তের চিত্র :

বর্গক্ষেত্রের পরিবৃত্তের চিত্র :

ধরি, বর্গক্ষেত্রের বাহুর দৈর্ঘ্য a একক, বর্গক্ষেত্রের অন্তর্বৃত্তের ব্যাসার্ধ r একক এবং পরিবৃত্তের ব্যাসার্ধ R একক ।

আমরা জানি,

বর্গক্ষেত্রের অন্তর্বৃত্তের ব্যাস, বর্গক্ষেত্রের বাহুর দৈর্ঘ্যের সমান হয়।

অর্থাৎ,

2r = a

$\therefore r=\frac{a}{2}$

আবার,

বর্গক্ষেত্রের পরিবৃত্তের ব্যাস, বর্গক্ষেত্রের কর্ণের দৈর্ঘ্যের সমান হয়।

অর্থাৎ,

$2R=a\sqrt{2}$

$\therefore R=\frac{a\sqrt{2}}{2}$

∴ বর্গক্ষেত্রের অন্তর্বৃত্ত ও পরিবৃত্তের ব্যাসার্ধের অনুপাত

$=\frac{a}{2}:\frac{a\sqrt{2}}{2}$

$=1:\sqrt{2}$

উত্তরঃ বর্গক্ষেত্রের অন্তর্বৃত্ত ও পরিবৃত্তের ব্যাসার্ধের অনুপাত ${\color{DarkGreen} 1:\sqrt{2}}$

20. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ

(iv) একটি ঘড়ির মিনিটের কাঁটার দৈর্ঘ্য 7 সেমি.। 15 মিনিটে কাঁটাটি কত দৈর্ঘ্য ঘুরবে ?

সমাধানঃ

প্রদত্ত,

ঘড়ির মিনিটের কাঁটার ব্যাসার্ধ (r) = 7 সেমি.

∴ ঘড়িটির পরিধি

$=2\pi r$

$=2\times \frac{22}{7}\times 7$

= 44 সেমি.

মিনিটের কাঁটাটি সম্পূর্ণ ঘড়িটি একবার ঘুরে আসতে 60 মিনিট সময় নেয়।

অর্থাৎ, কাঁটাটি 60 মিনিটে যায় 44 সেমি.

1 মিনিটে যায় $\frac{44}{60}$ সেমি.

∴ 15 মিনিটে যায়

$=\frac{44\times 15}{60}$ সেমি.

= 11 সেমি.

উত্তরঃ 15 মিনিটে কাঁটাটি 11 সেমি. দৈর্ঘ্য ঘুরবে।

20. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্নঃ

(v) একটি বৃত্তের ব্যাসের দৈর্ঘ্য এবং একটি বর্গক্ষেত্রের বাহুর দৈর্ঘ্য সমান হলে তাদের পরিসীমার অনুপাত কত ?

সমাধানঃ

ধরি, বৃত্তটির ব্যাসার্ধ r একক

∴ ব্যাস = 2r একক

ও পরিসীমা = 2πr একক

ধরি, বর্গক্ষেত্রের বাহুর দৈর্ঘ্য a একক

∴ বর্গক্ষেত্রের পরিসীমা = 4a একক

প্রশ্নানুসারে,

a = 2r

∴ বৃত্ত ও বর্গক্ষেত্রের পরিসীমার অনুপাত

= 2πr : 4a

= 2πr : 4 × 2r [ a = 2r বসিয়ে পাই ]

= 2πr : 8r

= π : 4

$=\frac{22}{7}:4$

$=\frac{11}{7}:2$

$=\frac{11}{7}\times 7:2\times 7$

= 11 : 14

উত্তরঃ বৃত্ত ও বর্গক্ষেত্রের পরিসীমার অনুপাত 11 : 14