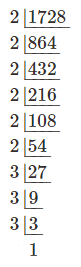Koshe dekhi 21 class 9
Koshe dekhi 21 class 9
| 1. মান নির্ণয় করি :
(i) সমাধানঃ
= −3 × (1) = −3 (উত্তর) |
| 1. মান নির্ণয় করি :
(ii) সমাধানঃ
= 3 (উত্তর) অথবা = 3 log0.01 0.01 = 3 |
| 1. মান নির্ণয় করি :
(iii) সমাধানঃ
= 6 (উত্তর) |
| 1. মান নির্ণয় করি :
(iv) সমাধানঃ
∴ 1728 = 26 × 33 = 26 × (√3)6 = (2√3)6 এখন, = 6 (উত্তর) |
| 2. (a) 625 -এর লগারিদম 4 হলে, নিধান কি হবে হিসাব করে লিখি।
সমাধানঃ ধরি, নিধান হল ‘x‘ ∴ logx 625 = 4 বা, x4 = 625 [যেহেতু, loga b = c হলে, ac = b হয়] বা, x4 = 5 × 5 × 5 × 5 বা, x4 = 54 ∴ x = 5 উত্তরঃ নির্ণেয় নিধান হল 5 |
| 2. (b) 5832 -এর লগারিদম 6 হলে, নিধান কি হবে হিসাব করে লিখি।
সমাধানঃ ধরি, নিধান হলো ‘x‘ ∴ logx 5832 = 6 বা, x6 = 5832 [যেহেতু, loga b = c হলে, ac = b হয়] বা, x6 = 2 × 2 × 2 × 3 × 3 × 3 × 3 × 3 × 3 বা, x6 = (3√2)6 ∴ x = 3√2 উত্তরঃ নির্ণেয় নিধান হল 3√2 |
| 3. (a) সমাধানঃ
বা, 1 = 2 log10 b − log10 a বা, log10 10 = log10 b2 − log10 a বা, বা,
|
| 3. (b) সমাধানঃ বা, বা, বা, বা, বা,
|
| 4. মান নির্ণয় করি :
(a) সমাধানঃ
= 0 |
| 4. মান নির্ণয় করি :
(b) সমাধানঃ
|
| 4. মান নির্ণয় করি :
(c) সমাধানঃ [ধরি, প্রতিটির log এর নিধান একই] = 1 (উত্তর) |
| 4. মান নির্ণয় করি :
(d) সমাধানঃ
= 2 (উত্তর) |
| 5. প্রমাণ করি :
(i) সমাধানঃ বামপক্ষ : = log 2 = ডানপক্ষ (প্রমাণিত) |
| 5. প্রমাণ করি :
(ii) সমাধানঃ বামপক্ষ :
= 2 = ডানপক্ষ (প্রমাণিত) |
| 5. প্রমাণ করি :
(iii) সমাধানঃ বামপক্ষ :
= 1 + 4 = 5 = ডানপক্ষ (প্রমাণিত) |
| 5. প্রমাণ করি :
(iv) সমাধানঃ বামপক্ষ :
= ডানপক্ষ (প্রমাণিত) |
| 5. প্রমাণ করি :
(v) সমাধানঃ বামপক্ষ : = ডানপক্ষ (প্রমাণিত) |
Koshe dekhi 21 class 9
| 5. প্রমাণ করি :
(vi) সমাধানঃ বামপক্ষ :
= 2 = ডানপক্ষ (প্রমাণিত) |
Koshe dekhi 21 class 9
| 5. প্রমাণ করি :
(vii) সমাধানঃ বামপক্ষ : = 0 = ডানপক্ষ (প্রমাণিত) |
Koshe dekhi 21 class 9
| 5. প্রমাণ করি :
(viii) xlog y − log z × ylog z − log x × zlog x − log y = 1 সমাধানঃ ধরি, k = xlog y − log z × ylog z − log x × zlog x − log y উভয়পক্ষে log নিয়ে পাই, log k = log (xlog y − log z × ylog z − log x × zlog x − log y) বা, log k = (log y − log z) log x + (log z − log x) log y + (log x − log y) log z বা, log k = log y log x − log z log x + log z log y − log y log x + log z log x − log z log y বা, log k = 0 বা, log k = log 1 ∴ k = 1 ∴ xlog y − log z × ylog z − log x × zlog x − log y = 1 বামপক্ষ = ডানপক্ষ (প্রমাণিত) |
Koshe dekhi 21 class 9
| 6.(i) যদি সমাধানঃ বা, বা, বা, বা, বা, x2 + 2xy + y2 = 25xy বা, x2 + y2 = 25xy − 2xy বা, x2 + y2 = 23xy বা, বা,
|
Koshe dekhi 21 class 9
| 6(ii) যদি a4 + b4 = 14a2 b2 হয়, তাহলে দেখাই যে log (a2 + b2 ) = log a + log b + 2 log 2
সমাধানঃ a4 + b4 = 14a2 b2 বা, (a2 + b2 )2 − 2a2 b2 = 14a2 b2 বা, (a2 + b2 )2 = 14a2 b2 + 2a2 b2 বা, (a2 + b2 )2 = 16a2 b2 বা, (a2 + b2 )2 = (4ab)2 বা, a2 + b2 = 4ab উভয়পক্ষে log নিয়ে পাই, log (a2 + b2) = log (4ab) বা, log (a2 + b2) = log 4 + log a + log b বা, log (a2 + b2) = log 22 + log a + log b বা, log (a2 + b2) = 2 log 2 + log a + log b ∴ log (a2 + b2 ) = log a + log b + 2 log 2 (প্রমাণিত) |
Koshe dekhi 21 class 9
| 7. যদি সমাধানঃ ধরি, ∴ log x = k (y − z), log y = k (z − x) এবং log z = k (x − y) এখন, log x + log y + log z = k (y − z) + k (z − x) + k (x − y) বা, log (xyz) = k (y − z + z − x + x − y) বা, log (xyz) = k × 0 বা, log (xyz) = 0 বা, log (xyz) = log 1 ∴ xyz = 1 (প্রমাণিত) |
Koshe dekhi 21 class 9
| 8. (a) যদি xb + c . yc + a . za + b = 1 সমাধানঃ ধরি, ∴ log x = k (b − c) উভয়দিকে (b + c) গুণ করে পাই, বা, (b + c)log x = k (b − c) (b + c) বা, log x(b + c) = k (b2 − c2) অনুরূপ ভাবে, log y(c + a) = k (c2 − a2) এবং log z(a + b) = k (a2 − b2) এখন, log x(b + c) + log y(c + a) + log z(a + b) = k (b2 − c2) + k (c2 − a2) + k (a2 − b2) বা, log x(b + c) × y(c + a) × z(a + b) = k (b2 − c2 + c2 − a2 + a2 − b2) বা, log x(b + c) × y(c + a) × z(a + b) = k × 0 বা, log x(b + c) . y(c + a) . z(a + b) = 0 বা, log x(b + c) . y(c + a) . z(a + b) = log 1 ∴ xb + c . yc + a . za + b = 1 (প্রমাণিত) |
| 8.(b) যদি সমাধানঃ ধরি, ∴ log x = k (b − c) উভয়দিকে (b2 + bc + c2) গুণ করে পাই, বা, (b2 + bc + c2)log x = k (b − c) (b2 + bc + c2) বা, অনুরূপ ভাবে,
এখন,
বা,
বা, বা, বা,
|
| 9. যদি a3 − x . b5x = a5 + x . b3x হয়, তাহলে দেখাই যে সমাধানঃ a3 − x . b5x = a5 + x . b3x বা, বা, b5x − 3x = a5+x − 3+x বা, b2x = a2 + 2x বা, b2x = a2 . a2x বা, বা, a3 − x . b5x = a5 + x . b3x বা, বা, b5x − 3x = a5+x − 3+x বা, b2x = a2 + 2x বা, b2x = a2 . a2x বা, বা, বা, বা, উভয়দিকে log নিয়ে পাই, বা,
|
| 10. সমাধান করি :
(a) সমাধানঃ বা, বা, বা, বা, বা, বা, বা, 4x + 17 = 81 বা, 4x = 81 − 17 বা, 4x = 64 বা, 4x = 43 ∴ x = 3 (উত্তর) |
| 10. সমাধান করি :
(b) log8 x + log4 x + log2 x = 11 সমাধানঃ log8 x + log4 x + log2 x = 11 বা, বা, বা, বা, বা, বা, বা, বা, বা, log x = 6 log 2 বা, log x = log 26 বা, x = 26 ∴ x = 64 (উত্তর) |
| 11. দেখাই log10 2 -এর মান সমাধানঃ ধরি, x = log10 2 ∴ 10x = 2 [যেহেতু, loga b = c হলে, ac = b হয়] বা, 1012x = 212 বা, 1012x = 4096 এখন, 1000 < 4096 < 10000 = 103 < 4096 < 104 = 103 < 1012x < 104 = 3 < 12x < 4
|
Koshe dekhi 21 class 9
| 12. বহু বিকল্পীয় প্রশ্ন (M.C.Q)
(i) যদি log√x 0.25 = 4 হয়, তাহলে x -এর মান (a) 0.5 (b) 0.25 (c) 4 (d) 16 সমাধানঃ log√x 0.25 = 4 বা, (√x)4 = 0.25 [যেহেতু, loga b = c হলে, ac = b হয়] বা, x2 = (0.5)2 ∴ x = 0.5 উত্তরঃ (a) 0.5 |
Koshe dekhi 21 class 9
| 12. বহু বিকল্পীয় প্রশ্ন (M.C.Q)
(ii) log10 (7x − 5) = 2 হলে, x -এর মান (a) 10 (b) 12 (c) 15 (d) 18 সমাধানঃ log10 (7x − 5) = 2 বা, 102 = (7x − 5) [যেহেতু, loga b = c হলে, ac = b হয়] বা, 100 = (7x − 5) বা, 100 + 5 = 7x বা, 105 = 7x বা, ∴ x = 15 উত্তরঃ (c) 15 |
Koshe dekhi 21 class 9
| 12. বহু বিকল্পীয় প্রশ্ন (M.C.Q)
(iii) log2 3 = a হলে, log8 27 হবে (a) 3a (b) (c) 2a (d) a সমাধানঃ log8 27 = log2 3 = a উত্তরঃ (d) a |
Koshe dekhi 21 class 9
| 12. বহু বিকল্পীয় প্রশ্ন (M.C.Q)
(iv) log√2 x = a হলে, log2√2 x হবে (a) (b) a (c) 2a (d) 3a সমাধানঃ log2√2 x উত্তরঃ (a) |
Koshe dekhi 21 class 9
| 12. বহু বিকল্পীয় প্রশ্ন (M.C.Q)
(v) (a) 27 (b) 9 (c) 3 (d) সমাধানঃ বা, বা, বা, বা, x = 33 ∴ x = 27 উত্তরঃ (a) 27 |
Koshe dekhi 21 class 9
| 13. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন :
(i) log4 log4 log4 256 -এর মান কত হবে হিসাব করি। সমাধানঃ log4 log4 log4 256
= 0 (উত্তর) |
Koshe dekhi 21 class 9
| 13. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন :
(ii) সমাধানঃ
= log an − log bn + log bn − log cn + log cn − log an = 0 (উত্তর) |
Koshe dekhi 21 class 9
| 13. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন :
(iii) দেখাই যে সমাধানঃ ধরি, উভয়পক্ষে log নিয়ে পাই, বা, বা, বা, log k = log x বা, k = x |
Koshe dekhi 21 class 9
| 13. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন :
(iv) loge 2. logx 25 = log10 16. loge 10 হলে, x -এর মান নির্ণয় করি। সমাধানঃ loge 2. logx 25 = log10 16. loge 10 বা, বা, বা, বা, বা, বা, বা, x4 = 25 বা, x4 = (√5)4 ∴ x = √5 (উত্তর) |
Koshe dekhi 21 class 9
Support Me
If you like my work then you can Support me by contributing a small amount which will help me a lot to grow my Website. It’s a request to all of you. You can donate me through phone pay / Paytm/ Gpay on this number 7980608289 or by the link below :
and visit Our website : learningscience.co.in
গণিত প্রকাশ (দশম শ্রেণী) সম্পূর্ণ সমাধান
গণিত প্রকাশ (নবম শ্রেণী) সম্পূর্ণ সমাধান
গণিত প্রভা (ষষ্ঠ শ্রেণী) সম্পূর্ণ সমাধান