Koshe Dekhi 23.1 Class 10

koshe dekhi 23.1 class 10

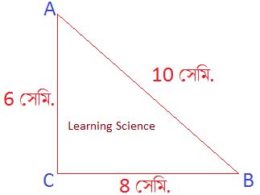
ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.1

Q1. একটি সমকোণী ত্রিভুজ ABC এঁকেছি যার অতিভুজ AB = 10 সেমি., ভূমি BC = 8 সেমি. এবং লম্ব AC = 6 সেমি.। ∠ABC এর Sine এবং Tangent -এর মান নির্ণয় করি।

উত্তরঃ $\small sin\angle ABC=\frac{3}{5}$ এবং $\small tan\angle ABC=\frac{3}{4}$

সমাধানঃ

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.1

∵ অতিভুজ = AB = 10 সেমি.

∴ $\small \bg_white \angle ACB=90 \degree$

এখন, ΔABC -এর, ∠ABC -এর সাপেক্ষে লম্ব = AC = 6 সেমি., ভূমি = BC = 8 সেমি.

∵ আমরা জানি,

$sin \theta$

∴ ∠ABC -এর সাপেক্ষে Sine,

$\small sin\angle ABC=\frac{6}{10}\Leftrightarrow \frac{3}{5}$

∴ $\small sin\angle ABC=\frac{3}{5}$ (উত্তর)

∵ আমরা জানি,

$tan \theta$

∴ ∠ABC -এর সাপেক্ষে Tangent,

$\small tan\angle ABC=\frac{6}{8}\Leftrightarrow \frac{3}{4}$

∴ $\small tan\angle ABC=\frac{3}{4}$ (উত্তর)

koshe dekhi 23.1 class 10

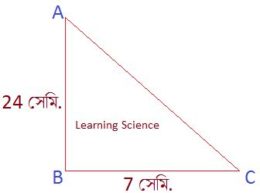
ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.1

Q2. সোমা একটি সমকোণী ত্রিভুজ ABC এঁকেছে যার ∠ABC = 90°, AB = 24 সেমি. এবং BC = 7 সেমি.। হিসাব করে sinA, cosA, tanA ও cosecA – এর মান লিখি।

উত্তরঃ $\small sin A=\frac{7}{25}$ ; $\small cos A=\frac{24}{25}$ ; $\small tan A=\frac{7}{24}$ এবং $\small cosec A=\frac{25}{7}$

সমাধানঃ

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.1

∵ $\small \bg_white \angle ABC=90 \degree$

∴ অতিভুজ = AC

∠A -এর সাপেক্ষে, লম্ব = BC = 7 সেমি., ভূমি = AB = 24 সেমি.

পিথাগোরাসের সমীকরণ অনুযায়ী,

(লম্ব)² + (ভূমি)² = (অতিভুজ)²

বা, (BC)² + (AB)² = (AC)²

বা, (7)² + (24)² = (AC)²

বা, 49 + 576 = (AC)²

বা, (AC)² = 625

বা, $\small AC=\sqrt{625}\Rightarrow 25$ সেমি.

∴ অতিভুজ = AC = 25 সেমি.

এখন, যেহেতু

$sin \theta$

∴ ∠A -এর সাপেক্ষে Sine,

$\small sinA=\frac{BC}{AC}$

$\small \therefore sin A=\frac{7}{25}$ (উত্তর)

আবার, যেহেতু

$cos \theta$

∴ ∠A -এর সাপেক্ষে Cosine,

$\small cosA=\frac{AB}{AC}$

$\small \therefore cos A=\frac{24}{25}$ (উত্তর)

আবার, যেহেতু

$tan \theta$

∴ ∠A -এর সাপেক্ষে Tangent,

$\small tanA=\frac{BC}{AB}$

$\small \therefore tan A=\frac{7}{24}$ (উত্তর)

আবার, যেহেতু

$cosec \theta$

∴ ∠A -এর সাপেক্ষে Cosecant,

$\small cosecA=\frac{AC}{BC}$

$\small \therefore cosec A=\frac{25}{7}$ (উত্তর)

koshe dekhi 23.1 class 10

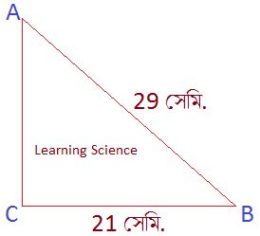
ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.1

Q3. যদি ABC একটি সমকোণী ত্রিভুজের ∠C = 90°, BC = 21 একক এবং AB = 29 একক হয়, তাহলে sinA, cosA, sinB ও cosB – এর মান নির্ণয় করি।

উত্তরঃ $\small sin A=\frac{21}{29}$ ; $\small cos A=\frac{20}{29}$ ; $\small sinB=\frac{20}{29}$ এবং $\small cosB=\frac{21}{29}$

সমাধানঃ

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.1

∵ $\small \bg_white \angle ACB=90 \degree$

∴ অতিভুজ = AB = 29 সেমি.

পিথাগোরাসের সমীকরণ অনুযায়ী,

(লম্ব)² + (ভূমি)² = (অতিভুজ)²

বা, (BC)² + (AC)² = (AB)²

বা, (21)² + (AC)² = (29)²

বা, 441 + (AC)² = 841

বা, (AC)² = 841 − 441

বা, (AC)² = 400

বা, $\small AC=\sqrt{400}\Rightarrow 20$ সেমি.

∴ অতিভুজ = AB = 29 সেমি. এবং ∠A এর সাপেক্ষে, লম্ব = BC = 21 সেমি., ভূমি = AC = 20 সেমি.

এখন, যেহেতু

$sin \theta$

∴ ∠A -এর সাপেক্ষে Sine,

$\small sinA=\frac{BC}{AB}$

$\small \therefore sin A=\frac{21}{29}$ (উত্তর)

আবার, যেহেতু

$cos \theta$

∴ ∠A -এর সাপেক্ষে Cosine,

$\small cosA=\frac{AC}{AB}$

$\small \therefore cos A=\frac{20}{29}$ (উত্তর)

আবার, অতিভুজ = AB = 29 সেমি. এবং ∠B এর সাপেক্ষে, লম্ব = AC = 20 সেমি., ভূমি = BC = 21 সেমি.

এখন, যেহেতু

$sin \theta$

∴ ∠B -এর সাপেক্ষে Sine,

$\small sinB=\frac{AC}{AB}$

$\small \therefore sin B=\frac{20}{29}$ (উত্তর)

আবার, যেহেতু

$cos \theta$

∴ ∠B -এর সাপেক্ষে Cosine,

$\small cosA=\frac{BC}{AB}$

$\small \therefore cos B=\frac{21}{29}$ (উত্তর)

koshe dekhi 23.1 class 10

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.1

Q4. যদি $\small {\color{Blue} cos\theta =\frac{7}{25}}$ হয়, তাহলে θ কোণের সকল ত্রিকোণমিতিক অনুপাতের মান নির্ণয় করি।

উত্তরঃ $\small sin\theta =\frac{24}{25}$ ; $\small cosec\theta =\frac{25}{24}$ ; $\small sec\theta =\frac{25}{7}$ ; $\small tan\theta =\frac{24}{7}$ এবং $\small cot\theta =\frac{7}{24}$

সমাধানঃ

প্রদত্ত, $cos\theta =\frac{7}{25}$

এখন, যেহেতু

$cos \theta$

∴ ধরি, ভূমি = 7k এবং অতিভুজ = 25k

পিথাগোরাসের সমীকরণ অনুযায়ী,

(লম্ব)² + (ভূমি)² = (অতিভুজ)²

বা, (লম্ব)² + (7k)² = (25k)²

বা, (লম্ব)² + 49k² = 625k²

বা, (লম্ব)² = 625k² − 49k²

বা, (লম্ব)² = 576k²

বা, লম্ব = $\bg_white \sqrt{576k^{2}}\Rightarrow 24k$

θ কোণের সাপেক্ষে,

লম্ব = 24k,

ভূমি = 7k এবং

অতিভুজ = 25k

∵ আমরা জানি,

$sin \theta$

$\small \therefore sin\theta =\frac{24k}{25k}\Leftrightarrow \frac{24}{25}$ (উত্তর)

∵ আমরা জানি,

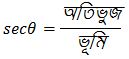
$cosec \theta$

$\small \therefore cosec\theta =\frac{25k}{24k}\Leftrightarrow \frac{25}{24}$ (উত্তর)

∵ আমরা জানি,

$sec \theta$

$\small \therefore sec\theta =\frac{25k}{7k}\Leftrightarrow \frac{25}{7}$ (উত্তর)

∵ আমরা জানি,

$tan \theta$

$\small \therefore tan\theta =\frac{24k}{7k}\Leftrightarrow \frac{24}{7}$ (উত্তর)

∵ আমরা জানি,

$cot \theta$

$\small \therefore cot\theta =\frac{7k}{24k}\Leftrightarrow \frac{7}{24}$ (উত্তর)

koshe dekhi 23.1 class 10

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.1

Q5. যদি cotθ = 2 হয়, তাহলে tanθ ও secθ -এর মান নির্ণয় করি এবং দেখাই 1 + tan²θ = sec²θ.

উত্তরঃ $\small tan \theta =\frac{1}{2}$ এবং $\small sec \theta = \frac{\sqrt{5}}{2}$

সমাধানঃ

প্রদত্ত, cotθ = 2 $\bg_white \Rightarrow \frac{2}{1}$

$cot \theta$

∴ ধরি, ভূমি = 2k এবং লম্ব = k

পিথাগোরাসের সমীকরণ অনুযায়ী,

(লম্ব)² + (ভূমি)² = (অতিভুজ)²

বা, (k)² + (2k)² = (অতিভুজ)²

বা, k² + 4k² = (অতিভুজ)²

বা, (অতিভুজ)² = 5k²

বা, অতিভুজ = $\bg_white \sqrt{5k^{2}}\Rightarrow k\sqrt{5}$

θ কোণের সাপেক্ষে,

লম্ব = k,

ভূমি = 2k এবং

অতিভুজ = $\small \mathbf{k\sqrt{5}}$

∵ আমরা জানি,

$tan \theta$

∴ $\small tan\theta =\frac{k}{2k}\Leftrightarrow \frac{1}{2}$ (উত্তর)

∵ আমরা জানি,

$sec \theta$

∴ $\small sec\theta =\frac{k\sqrt{5}}{2k}\Leftrightarrow \frac{\sqrt{5}}{2}$ (উত্তর)

বামপক্ষ :

1 + tan²θ

$\small =1+\left ( \frac{1}{2} \right )^{2}$ [ $\small {\color{Blue} \because tan\theta =\frac{1}{2}}$ ]

$\small =1+\frac{1}{4}$

$\small =\frac{\left (1\times 4 \right )+1}{4}$

$\small =\frac{4+1}{4}$

$\small =\frac{5}{4}$

ডানপক্ষ :

sec²θ

$\small =\left ( \frac{\sqrt{5}}{2} \right )^{2}$ [ $\small {\color{Blue} \because sec\theta =\frac{\sqrt{5}}{2}}$ ]

$\small =\frac{5}{4}$

∴ বামপক্ষ = ডানপক্ষ (প্রমানিত)

koshe dekhi 23.1 class 10

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.1

Q6. cosθ = 0.6 হলে, দেখাই যে 5 sinθ − 3 tanθ = 0.

উত্তরঃ sin ∠ABC = 25° এবং tan ∠ABC =

সমাধানঃ

প্রদত্ত, $\small cos \theta = 0.6\Leftrightarrow \frac{6}{10}=\frac{3}{5}$

এখন, যেহেতু

$cos \theta$

∴ ধরি, ভূমি = 3k এবং অতিভুজ = 5k

পিথাগোরাসের সমীকরণ অনুযায়ী,

(লম্ব)² + (ভূমি)² = (অতিভুজ)²

বা, (লম্ব)² + (3k)² = (5k)²

বা, (লম্ব)² + 3²k² = 25k²

বা, (লম্ব)² = 25k² − 9k²

বা, (লম্ব)² = 16k²

বা, লম্ব = $\small \bg_white \sqrt{16k^{2}}\Rightarrow 4k$

θ কোণের সাপেক্ষে,

লম্ব = 4k,

ভূমি = 3k এবং

অতিভুজ = 5k

∵ আমরা জানি,

$sin \theta$

∴ $\small sin \theta = \frac{4k}{5k}\Leftrightarrow \frac{4}{5}$

∵ আমরা জানি,

$tan \theta$

∴ $\small tan \theta = \frac{4k}{3k}\Leftrightarrow \frac{4}{3}$

বামপক্ষ :

5 sinθ − 3 tanθ

মান বসিয়ে পাই –

$\small =5\times \left (\frac{4}{5} \right )-3\times \left (\frac{4}{3} \right )$

$\small =4-3$

$\small =1$ = ডানপক্ষ (প্রমানিত)

koshe dekhi 23.1 class 10

[/su_box]

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.1

Q7. যদি $\small {\color{Blue} cotA=\frac{4}{7.5}}$ হয়, তাহলে cosA এবং cosecA এর মান নির্ণয় করি এবং দেখাই যে 1 + cot²A = cosec²A.

উত্তরঃ sin ∠ABC = 25° এবং tan ∠ABC =

সমাধানঃ

প্রদত্ত, $cotA=\frac{4}{7.5}$ $\bg_white \Rightarrow \frac{40}{75}\Rightarrow \frac{8}{15}$

$cot \theta$

∴ ধরি, ভূমি = 8k এবং লম্ব = 15k

পিথাগোরাসের সমীকরণ অনুযায়ী,

(লম্ব)² + (ভূমি)² = (অতিভুজ)²

বা, (15k)² + (8k)² = (অতিভুজ)²

বা, 225k² + 64k² = (অতিভুজ)²

বা, (অতিভুজ)² = 289k²

বা, অতিভুজ $=\sqrt{289k^{2}}=17k$

আমরা জানি,

$cos \theta$

$\small \therefore cosA=\frac{8k}{17k}=\frac{8}{17}$

(উত্তর)

এবং

$cosec \theta$

$\therefore cosecA=\frac{17k}{15k}=\frac{17}{15}$

(উত্তর)

বামপক্ষ :

1 + cot²A

$=1+\left ( \frac{8}{15} \right )^{2}$

$=1+\frac{64}{225}$

$=\frac{225+64}{225}$

$=\frac{289}{225}$

ডানপক্ষ :

cosec²A

$=\left ( \frac{17}{15} \right )^{2}$

$=\frac{289}{225}$

বামপক্ষ = ডানপক্ষ (প্রমানিত)

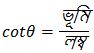
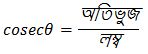
koshe dekhi 23.1 class 10

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.1

Q8. যদি $\small {\color{Blue} sinC=\frac{2}{3}}$ হয়, তবে cosC × cosecC -এর মান হিসাব করে লিখি।

উত্তরঃ sin ∠ABC = 25° এবং tan ∠ABC =

সমাধানঃ

প্রদত্ত, $sinC=\frac{2}{3}$

যেহেতু,

$sin \theta$

ধরি, লম্ব = 2k এবং অতিভুজ = 3k

পিথাগোরাসের সমীকরণ অনুযায়ী,

(লম্ব)² + (ভূমি)² = (অতিভুজ)²

বা, (2k)² + (ভূমি)² = (3k)²

বা, 4k² + (ভূমি)² = 9k²

বা, (ভূমি)² = 9k² − 4k²

বা, (ভূমি)² = 5k²

বা, ভূমি = $\sqrt{5k^{2}}\Rightarrow k\sqrt{5}$

আমরা জানি,

$cos \theta$

$\small \therefore cosC=\frac{k\sqrt{5}}{3k}$

$\small =\frac{\sqrt{5}}{3}$

আবার,

আমরা জানি,

$cosec \theta$

$\small \therefore cosecC=\frac{3k}{2k}$

$\small =\frac{3}{2}$

এখন,

নির্ণেয়, cosC × cosecC

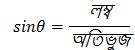
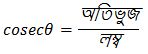
$\small =\frac{\sqrt{5}}{3}\times \frac{3}{2}$ $\small =\frac{\sqrt{5}}{2}$ Answer

koshe dekhi 23.1 class 10

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.1

Q9. নীচের বিবৃতিগুলো সত্য না মিথ্যা তা যুক্তি সহকারে লিখি।

(i) tanA -এর মান সর্বদা 1 অপেক্ষা বড়ো।

উত্তরঃ প্রদত্ত বিবৃতিটি মিথ্যা।

ব্যাখ্যা :

$tan \theta$

সুতরাং, যখন লম্ব > ভূমি হবে, তখন tanA এর মান 1 অপেক্ষা বড়ো হবে।

যখন লম্ব = ভূমি হবে, তখন tanA এর মান 1 এর সমান হবে।

যখন লম্ব < ভূমি হবে, তখন tanA এর মান 1 অপেক্ষা ছোট হবে।

∵ tanA -এর মান 1 এর সমান, বড়ো বা ছোট হতে পারে কিন্তু প্রদত্ত বিবৃতিটি হলো “tanA -এর মান সর্বদা 1 অপেক্ষা বড়ো।“

∴ প্রদত্ত উক্তিটি মিথ্যা।

koshe dekhi 23.1 class 10

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.1

Q9. নীচের বিবৃতিগুলো সত্য না মিথ্যা তা যুক্তি সহকারে লিখি।

(ii) cotA -এর মান সর্বদা 1 অপেক্ষা ছোটো।

উত্তরঃ প্রদত্ত বিবৃতিটি মিথ্যা।

ব্যাখ্যা :

$cot \theta$

সুতরাং, যখন ভূমি > লম্ব হবে, তখন cotA এর মান 1 অপেক্ষা বড়ো হবে।

যখন ভূমি = লম্ব হবে, তখন cotA এর মান 1 এর সমান হবে।

যখন ভূমি < লম্ব হবে, তখন cotA এর মান 1 অপেক্ষা ছোট হবে।

∵ cotA -এর মান 1 এর সমান, বড়ো বা ছোট হতে পারে কিন্তু প্রদত্ত বিবৃতিটি হলো “cotA -এর মান সর্বদা 1 অপেক্ষা ছোটো”।

∴ প্রদত্ত উক্তিটি মিথ্যা।

koshe dekhi 23.1 class 10

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.1

Q9. নীচের বিবৃতিগুলো সত্য না মিথ্যা তা যুক্তি সহকারে লিখি।

(iii) একটি কোণ θ এর জন্য $\small {\color{Blue} sin\theta =\frac{4}{3}}$ হতে পারে।

উত্তরঃ প্রদত্ত বিবৃতিটি মিথ্যা।

ব্যাখ্যা :

$sin \theta$

এবং কোন সমকোণী ত্রিভুজের অতিভুজই হলো সবচেয়ে বড়ো বাহু।

∴ sinθ এর মান 1 অপেক্ষা ছোট কিন্তু প্রদত্ত $sin\theta =\frac{4}{3}$ অর্থাৎ 1 অপেক্ষা বড়ো।

সুতরাং, প্রদত্ত উক্তিটি কোণ θ এর জন্য মিথ্যা।

koshe dekhi 23.1 class 10

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.1

Q9. নীচের বিবৃতিগুলো সত্য না মিথ্যা তা যুক্তি সহকারে লিখি।

(iv) একটি কোণ α এর জন্য $\small {\color{Blue} sec\alpha =\frac{12}{5}}$ হতে পারে।

উত্তরঃ প্রদত্ত বিবৃতিটি সত্য।

ব্যাখ্যা :

$sec \theta$

এবং কোন সমকোণী ত্রিভুজের অতিভুজই হলো সবচেয়ে বড়ো বাহু।

∴ secθ এর মান 1 অপেক্ষা বড়ো এবং প্রদত্ত $sec\alpha =\frac{12}{5}$ অর্থাৎ 1 অপেক্ষা বড়ো।

সুতরাং, প্রদত্ত উক্তিটি কোণ α এর জন্য সত্য।

koshe dekhi 23.1 class 10

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.1

Q9. নীচের বিবৃতিগুলো সত্য না মিথ্যা তা যুক্তি সহকারে লিখি।

(v) একটি কোণ β(Beta) এর জন্য $\small {\color{Blue} cosec\beta =\frac{5}{13}}$ হতে পারে।

উত্তরঃ প্রদত্ত বিবৃতিটি মিথ্যা।

ব্যাখ্যা :

$cosec \theta$

এবং কোন সমকোণী ত্রিভুজের অতিভুজই হলো সবচেয়ে বড়ো বাহু।

∴ cosecβ এর মান সর্বদা 1 অপেক্ষা বড়ো কিন্তু প্রদত্ত $cosec\beta =\frac{5}{13}$ অর্থাৎ 1 অপেক্ষা ছোট।

সুতরাং, প্রদত্ত উক্তিটি কোণ β এর জন্য মিথ্যা।

koshe dekhi 23.1 class 10

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.1

Q9. নীচের বিবৃতিগুলো সত্য না মিথ্যা তা যুক্তি সহকারে লিখি।

(vi) একটি কোণ θ এর জন্য $\small {\color{Blue} cos\theta =\frac{3}{5}}$ হতে পারে।

উত্তরঃ প্রদত্ত বিবৃতিটি সত্য।

ব্যাখ্যা :

$cos \theta$

এবং কোন সমকোণী ত্রিভুজের অতিভুজই হলো সবচেয়ে বড়ো বাহু।

∴ cosθ এর মান 1 অপেক্ষা ছোট এবং প্রদত্ত $cos\theta =\frac{3}{5}$ অর্থাৎ 1 অপেক্ষা ছোট।

সুতরাং, প্রদত্ত উক্তিটি কোণ θ এর জন্য সত্য।

koshe dekhi 23.1 class 10

Thank You

Koshe Dekhi 23.1 Class 10

Koshe Dekhi 23.1 Class 10

koshe dekhi 23.1 class 10

koshe dekhi 23.1 class 10

Related Post

WBCHSE – Let us Work Out 26.4 – WB Class 10

WBCHSE – Let us Work Out 26.1 – WB Class 10

Koshe Dekhi 21 Class 10

2 thoughts on “Koshe Dekhi 23.1 Class 10”

Leave a Reply Cancel reply

You missed

Notification Out: RRB NTPC Recruitment 2024

CITL-001 Solved Assignment 2024-25

CIT-003 Solved Assignment 2024-25

CIT-002 Solved Assignment 2024-25