Koshe Dekhi 3.2 class 10
Koshe Dekhi 3.2 class 10
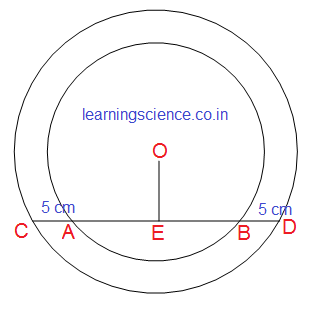
| Q1. O কেন্দ্রীয় একটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5 সেমি. এবং AB একটি একটি জ্যা এর দৈর্ঘ্য 8 সেমি.। O বিন্দু থেকে AB জ্যা এর দূরত্ব হিসাব করে লিখি। সমাধানঃ
|
Koshe dekhi 3.2 class 10
| Q2. O কেন্দ্রীয় একটি বৃত্তের ব্যাসের দৈর্ঘ্য 26 সেমি.। O বিন্দু থেকে PQ জ্যা এর দুরত্ব 5 সেমি.। PQ জ্যা এর দৈর্ঘ্য হিসাব করে লিখি। সমাধানঃ
|
| Q3. O কেন্দ্রীয় একটি বৃত্তের PQ জ্যা এর দৈর্ঘ্য 4 সেমি. এবং O বিন্দু থেকে PQ এর দূরত্ব 2.1 সেমি.। বৃত্তের ব্যাসের দৈর্ঘ্য হিসাব করে লিখি। সমাধানঃ
|
| Q4. O কেন্দ্রীয় বৃত্তে 6 সেমি. ও 8 সেমি. দৈর্ঘ্যের দুটি জ্যা। যদি ছোটো দৈর্ঘ্যের জ্যাটির বৃত্তের কেন্দ্র থেকে দূরত্ব 4 সেমি. হয়, তাহলে অপর জ্যাটির কেন্দ্র থেকে দূরত্ব কত তা হিসাব করে লিখি। সমাধানঃ
|
| Q5. যদি কোনো বৃত্তের একটি জ্যা এর দৈর্ঘ্য 48 সেমি. এবং কেন্দ্র থেকে ওই জ্যা এর দূরত্ব 7 সেমি. হয়, তবে ওই বৃত্তের কেন্দ্র থেকে যে জ্যা-এর দূরত্ব 20 সেমি. সেই জ্যা এর দৈর্ঘ্য কত হবে তা হিসাব করে লিখি। সমাধানঃ
|
Koshe dekhi 3.2 class 10
Q6. পাশের O কেন্দ্রীয় বৃত্তের ছবিতে 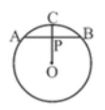 সমাধানঃ
|
Koshe dekhi 3.2 class 10
| Q7. একটি সরলরেখা দুটি এককেন্দ্রীয় বৃত্তের একটিকে A ও B বিন্দুতে এবং অপরটিকে C ও D বিন্দুতে ছেদ করেছে। যুক্তি দিয়ে প্রমান করি যে, AC = DB. সমাধানঃ
|
Koshe dekhi 3.2 class 10
| Q8. প্রমান করি, কোনো বৃত্তের দুটি পরস্পরছেদি জ্যা পরস্পরকে সমদ্বিখন্ডিত করতে পারে না, যদি না উভযেই বৃত্তের ব্যাস হয়। সমাধানঃ
|
Koshe dekhi 3.2 class 10
| Q9. X ও Y কেন্দ্রবিশিষ্ট দুটি বৃত্ত পরস্পরকে A ও B বিন্দুতে ছেদ করেছে। XY -এর মধ্যবিন্দু S -এর সঙ্গে A বিন্দু যুক্ত করলাম এবং A বিন্দু দিয়ে SA -এর উপর লম্ব অঙ্কন করলাম যা বৃত্ত দুটিকে P ও Q বিন্দুতে ছেদ করল। প্রমান করি যে, PA = AQ. সমাধানঃ
|
Koshe dekhi 3.2 class 10
| Q10. O কেন্দ্রীয় বৃত্তের 10 সেমি. ও 24 সেমি. দৈর্ঘ্যের দুটি সমান্তরাল জ্যা AB এবং CD কেন্দ্রের বিপরীত পার্শ্বে অবস্থিত। যদি AB ও CD -জ্যা দুটির মধ্যে দূরত্ব 17 সেমি. হয়, তবে হিসাব করে বৃত্তের ব্যাসার্ধের দৈর্ঘ্য লিখি। সমাধানঃ
|
Koshe dekhi 3.2 class 10
| Q11. দুটি বৃত্তের কেন্দ্র P এবং Q; বৃত্তদুটি A এবং B বিন্দুতে ছেদ করে। A বিন্দু দিয়ে PQ সরলরেখাংশের সমান্তরাল সরলরেখা বৃত্ত দুটিকে C ও D বিন্দুতে ছেদ করে। প্রমাণ করি যে, CD = 2PQ. সমাধানঃ
|
Koshe dekhi 3.2 class 10
| Q12. একটি বৃত্তের AB ও AC জ্যা দুটি সমান। প্রমাণ করি যে, সমাধানঃ
|
Koshe dekhi 3.2 class 10
| Q13. একটি বৃত্তের দুটি পরস্পরছেদী জ্যা এর অন্তর্ভুক্ত কোণের সমদ্বিখন্ডক যদি কেন্দ্রগামী হয়, তাহলে প্রমাণ করি যে, ত্যা দুটি সমান। সমাধানঃ
|
| Q14. প্রমাণ করি, একটি বৃত্তে দুটি জ্যা এর মধ্যে যে জ্যাটি কেন্দ্রের নিকটবর্তী সেটির দৈর্ঘ্য অপর জ্যা টির দৈর্ঘ্য অপেক্ষা বৃহত্তর। সমাধানঃ
|
| Q15. একটি বৃত্তের ভিতর যে-কোনো বিন্দু দিয়ে ক্ষুদ্রতম জ্যা কোনটি হবে তা প্রমাণ করে লিখি। সমাধানঃ
ধরি, O কেন্দ্রীয় বৃত্তের মধ্যস্থ M একটি যেকোনাে বিন্দু। M বিন্দুদিয়ে PQ একটি জ্যা, যেখানে M বিন্দুটি PQ এর মধ্যবিন্দু এবং M বিন্দুদিয়ে অপর একটি জ্যা RS টানা হলো, যেখানে PQ ≠ RS অঙ্কনঃ RS এর অপর ON লম্ব অঙ্কন করা হল। প্রমানঃ ∴ OM > ON আবার, ∴ PQ < RS অর্থাৎ, বৃত্তের ভিতর কোনাে বিন্দুদিয়ে অঙ্কিত জ্যাটি ক্ষুদতম হবে তখনই যখন ঐ বিন্দুটি জ্যার্টির মধ্যবিন্দু হবে। |
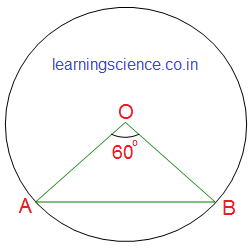
| Q16. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.) (A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) : (i) O কেন্দ্রীয় বৃত্তের AB ও CD জ্যা দুটির দৈর্ঘ্য সমান। ∠AOB = 60° হলে, ∠COD এর মান (a) 40° (b) 30° (c) 60° (d) 90° সমাধানঃ
|
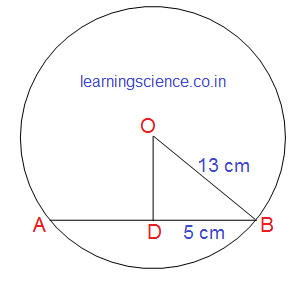
| Q16. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.) (A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) : (ii) একটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 13 সেমি. এবং বৃত্তের একটি জ্যা এর দৈর্ঘ্য 10 সেমি.। বৃত্তের কেন্দ্র থেকে জ্যা এর দূরত্ব (a) 12.5 সেমি. (b) 12 সেমি. (c) (d) 24 সেমি. সমাধানঃ
|
| Q16. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.) (A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) : (iii) O কেন্দ্রীয় বৃত্তের AB ও CD দুটি সমান দৈর্ঘ্যের জ্যা। O বিন্দু থেকে AB জ্যা এর দূরত্ব 4 সেমি. হলে, CD জ্যা এর দুরত্ব (a) 2 সেমি. (b) 4 সেমি. (c) 6 সেমি. (d) 8 সেমি. সমাধানঃ
|
| Q16. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.) (A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) : (iv) AB ও CD দুটি সমান্তরাল জ্যা এর প্রত্যেকটির দৈর্ঘ্য 16 সেমি.। বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 10 সেমি. হলে, জ্যা দুটির মধ্যে দুরত্ব (a) 12 সেমি. (b) 16 সেমি. (c) 20 সেমি. (d) 5 সেমি. সমাধানঃ
|
| Q16. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.) (A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) : (v) দুটি সমকেন্দ্রীয় বৃত্তের কেন্দ্র O; একটি সরলরেখা একটি বৃত্তকে A ও B বিন্দুতে এবং অপর বৃত্তকে C ও D বিন্দুতে ছেদ করে। AC = 5 সেমি. হলে, BD -এর দৈর্ঘ্য (a) 2.5 সেমি. (b) 5 সেমি. (c) 10 সেমি. (d) কোনোটিই নয় সমাধানঃ
|
| 16 (B) সত্য / মিথ্যা লিখি : (i) তিনটি সমরেখ বিন্দু দিয়ে যায় এরকম একটি বৃত্ত অঙ্কন করা যায়। সমাধানঃ “তিনটি সমরেখ বিন্দু দিয়ে যায় এরকম একটি বৃত্ত অঙ্কন করা যায়” – বিবৃতিটি মিথ্যা। ব্যাখ্যা : যেহেতু বৃত্তের উপর অবস্থিত যেকোনো বিন্দুর সঞ্চারপথ বক্ররেখা হয় তাই তিনটি সমরেখ বিন্দু কখনোই একটি বৃত্তের উপর অবস্থিত হতে পারে না। কিন্তু তিনটি অসমরেখ বিন্দু দিয়ে কেবলমাত্র একটি বৃত্ত অঙ্কন করা সম্ভব।
(ii) ABCDA ও ABCEA বৃত্ত দুটি একই বৃত্ত। সমাধানঃ “ABCDA ও ABCEA বৃত্ত দুটি একই বৃত্ত” – বিবৃতিটি সত্য। ব্যাখ্যা : ABCDA ও ABCEA – এর মধ্যে তিনটি সাধারণ বিন্দু (A, B, ও C) আছে এবং যেহেতু তিনটি অসমরেখ বিন্দু দিয়ে কেবলমাত্র একটি বৃত্ত অঙ্কন করা যায় তাই “ABCDA ও ABCEA বৃত্ত দুটি একই বৃত্ত”।
(iii) O কেন্দ্রীয় বৃত্তের AB এবং AC জ্যা দুটি OA ব্যাসার্ধের বিপরীত পার্শ্বে অবস্থিত হলে, সমাধানঃ O কেন্দ্রীয় বৃত্তের AB এবং AC জ্যা দুটি OA ব্যাসার্ধের বিপরীত পার্শ্বে অবস্থিত হলে, ব্যাখ্যা : AB = AC হলে বিবৃতি সত্য হতো। |
| 16 (C) শূন্যস্থান পূরণ করি : (i) O কেন্দ্রীয় বৃত্তে PQ ও RS জ্যা দুটির দৈর্ঘ্যের অনুপাত 1 : 1 হলে, সমাধানঃ O কেন্দ্রীয় বৃত্তে PQ ও RS জ্যা দুটির দৈর্ঘ্যের অনুপাত 1 : 1 হলে,
(ii) বৃত্তের কোনো জ্যা এর লম্বসমদ্বিখন্ডক ওই বৃত্তের ________। সমাধানঃ বৃত্তের কোনো জ্যা এর লম্বসমদ্বিখন্ডক ওই বৃত্তের কেন্দ্রগামী। |
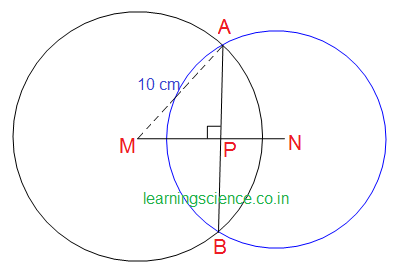
| Q17. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) : (i) 10 সেমি. দৈর্ঘ্যের ব্যাসার্ধের দুটি সমান বৃত্ত পরস্পরকে ছেদ করে এবং তাদের সাধারণ জ্যা এর দৈর্ঘ্য 12 সেমি.। বৃত্ত দুটির কেন্দ্রদ্বয়ের মধ্যে দূরত্ব নির্ণয় করি। সমাধানঃ
|
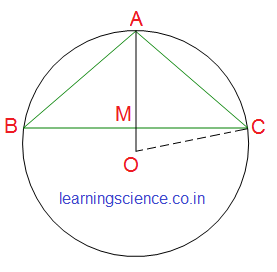
| Q17. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) : (ii) 5 সেমি. দৈর্ঘ্যের ব্যাসার্ধের একটি বৃত্তে AB এবং AC দুটি সমান দৈর্ঘ্যের জ্যা। বৃত্তের কেন্দ্র ABC ত্রিভুজের বাইরে অবস্থিত। AB = AC = 6 সেমি. হলে, BC জ্যা এর দৈর্ঘ্য নির্ণয় করি। সমাধানঃ
|
| Q17. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) : (iii) O কেন্দ্রীয় বৃত্তে AB ও CD জ্যা দুটির দৈর্ঘ্য সমান। সমাধানঃ
|
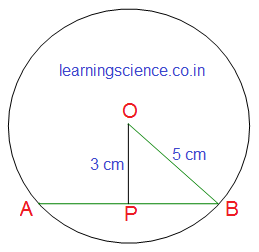
| Q17. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) : (iv) O কেন্দ্রীয় বৃত্তের ভিতর P যে-কোনো একটি বিন্দু। বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5 সেমি, এবং OP = 3 সেমি হলে, P বিন্দুগামী যে জ্যাটির দৈর্ঘ্য ন্যূনতম তা নির্ণয় করি। সমাধানঃ
|
| Q17. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) : (v) P ও Q কেন্দ্রবিশিষ্ট দুটি বৃত্ত A ও B বিন্দুতে ছেদ করে। A বিন্দু দিযে PQ -এর সমান্তরাল সরলরেখা বৃত্তদুটিকে যথাক্রমে C ও D বিন্দুতে ছেদ করে। PQ = 5 সেমি হলে, CD -এর দৈর্ঘ্য কত তা নির্ণয় করি। সমাধানঃ
|
and visit Our website : learningscience.co.in
গণিত প্রকাশ (দশম শ্রেণী) সম্পূর্ণ সমাধান
গণিত প্রকাশ (নবম শ্রেণী) সম্পূর্ণ সমাধান
গণিত প্রভা (ষষ্ঠ শ্রেণী) সম্পূর্ণ সমাধান
[adsense2]












































Very good👍
thnks
Best website for student👩🎓 who wants to be scholars
thnk u
Best explain, Thanks for help others.
Thank you for your valuable comment.
Your ‘thanks’ spelling is wrong.😅😅😅😅😅😅😅😆😆😆😆😆😆😂😂😂😂😂😂😂😊😊😊😊😆😆😆😆😆😆😆😆😆😆😆😆
Your ‘thanks’ spelling is wrong.😅😅😅😅😅😅😅😆😆😆😆😆😆😂😂😂😂😂😂😂😊😊😊😊😆😆😆😆😆😆😆😆😆😆😆😆