Koshe Dekhi 4 class 10
Koshe Dekhi 4 class 10
| Q1. আমরা পরিবেশের 4 টি আয়তঘনাকার ও 4 টি ঘনক আকার বস্তুর নাম লিখি।
উত্তরঃ আমাদের পরিবেশের 4 টি আয়তঘনাকার বস্তুর নাম হলঃ বই, ইট (Brick), দেশলাই বাক্স, চৌবাচ্চা। 4 টি ঘনক আকার বস্তুর নাম হলঃ লুডোর ছক্কা (Dice), ঘর, বই, রুবিক্স কিউব (Rubix Cube) |
Koshe dekhi 4 class 10
Q2. পাশের আয়তঘনাকার চিত্রের তলগুলি,ধারগুলি ও শীর্ষবিন্দুগুলির নাম লিখি।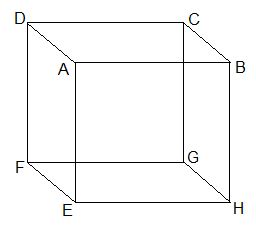
উত্তরঃ আয়তঘনাকার চিত্রটির তলগুলি হলঃ ABCD, EFGH, ABEH, BCGH, CDFG, ADFE ধারগুলি হলঃ AB, BC, CD, AD, AE, EF, FD, FG, CG, GH, BH, EH শীর্ষবিন্দুগুলি হলঃ A, B, C, D, E, F, G, H |
Koshe dekhi 4 class 10
| Q3. একটি সমকোণী চৌপলাকার ঘরের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 5 মি., 4 মি. ও 3 মি. হলে, ওই ঘরে সবচেয়ে লম্বা যে দন্ড রাখা যাবে তার দৈর্ঘ্য হিসাব করে লিখি।
সমাধানঃ প্রদত্ত, সমকোণী চৌপলাকার ঘরের দৈর্ঘ্য (l) = 5 মি. প্রস্থ (b) = 4 মি. উচ্চতা (h) = 3 মি. ঘরটিতে সবচেয়ে লম্বা যে দন্ড রাখা যাবে তার দৈর্ঘ্য ঘরটির কর্ণের দৈর্ঘ্যের সমান। আমরা জানি, সমকোণী চৌপলাকার ঘরের কর্ণের দৈর্ঘ্য, উত্তরঃ সমকোণী চৌপলাকার ঘরটিতে সবচেয়ে লম্বা যে দন্ড রাখা যাবে তার দৈর্ঘ্য |
Koshe dekhi 4 class 10
| Q4. একটি ঘনকের একটি তলের ক্ষেত্রফল 64 বর্গমিটার হলে, ঘনকটির আয়তন হিসাব করে লিখি।
সমাধানঃ প্রদত্ত, ঘনকের একটি তলের ক্ষেত্রফল = 64 বর্গমিটার ∴ ঘনকটির বাহুর দৈর্ঘ্য ∴ ঘনকটির আয়তন উত্তরঃ নির্ণেয় ঘনকের আয়তন 512 ঘনমিটার। |
Koshe dekhi 4 class 10
| Q5. আমাদের বকুলতলা গ্রামে 2 মিটার চওড়া এবং 8 ডেসিমি. গভীর একটি খাল কাটা হয়েছে। যদি মোট 240 ঘনমিটার মাটি কাটা হয়ে থাকে তবে খালটি কত লম্বা হিসাব করে লিখি।
সমাধানঃ ধরি, খালটি x মিটার লম্বা। প্রদত্ত, মাটি কাটা হয়েছে = 240 ঘনমিটার খালটি = 2 মিটার চওড়া খালটির গভীরতা = 8 ডেসিমি ∴ মাটি কাটা হয়েছে
প্রশ্নানুসারে, বা, বা, উত্তরঃ নির্ণেয় খালটি 150 মিটার লম্বা ছিল। |
Koshe dekhi 4 class 10
| Q6. একটি ঘনকের কর্ণের দৈর্ঘ্য সমাধানঃ ধরি, ঘনকের বাহুর দৈর্ঘ্য = a সেমি. প্রদত্ত, ঘনকের কর্ণের দৈর্ঘ্য আবার আমরা জানি, ঘনকের কর্ণের দৈর্ঘ্য বা, ∴ ঘনকটির সমগ্রতলের ক্ষেত্রফল উত্তরঃ নির্ণেয় ঘনকটির সমগ্রতলের ক্ষেত্রফল 96 বর্গসেমি.। |
Koshe dekhi 4 class 10
| Q7. একটি ঘনকের ধারগুলির দৈর্ঘ্যের সমষ্টি 60 সেমি. হলে, ঘনকটির ঘনফল হিসাব করে লিখি।
সমাধানঃ ধরি, ঘনকের বাহুর দৈর্ঘ্য = a সেমি. প্রদত্ত, ঘনকের ধারগুলির দৈর্ঘ্যের সমষ্টি 60 সেমি. ঘনকের মোট ধার সংখ্যা = 12 টি প্রশ্নানুসারে, \( 12\times a=60 \) \( \therefore a=\frac{60}{12}=5 \) ∴ ঘনকটির ঘনফল \( =\left ( a \right )^{3}=\left ( 5 \right )^{3}=125 \) ঘনসেমি.। উত্তরঃ নির্ণেয় ঘনকটির ঘনফল 125 ঘনসেমি.। |
Koshe dekhi 4 class 10
| Q8. যদি একটি ঘনকের 6 টি পৃষ্ঠতলের ক্ষেত্রফলের সমষ্টি 216 বর্গসেমি হয়, তবে ঘনকটির আয়তন কত হবে হিসাব করে লিখি।
সমাধানঃ ধরি, ঘনকের বাহুর দৈর্ঘ্য = a সেমি. প্রদত্ত, ঘনকের 6 টি পৃষ্ঠতলের ক্ষেত্রফলের সমষ্টি 216 বর্গসেমি.।
∴ ঘনকের প্রতিটি পৃষ্ঠতলের ক্ষেত্রফল ∴ ঘনকের বাহুর দৈর্ঘ্য ∴ ঘনকটির আয়তন উত্তরঃ নির্ণেয় ঘনকটির আয়তন 216 ঘনসেমি.। |
Koshe dekhi 4 class 10
| Q9. একটি সমকোণী চৌপলের আয়তন 432 ঘনসেমি.। তাকে সমান আয়তনবিশিষ্ট দুটি ঘনক-এ পরিনত করা হলে, প্রতিটি ঘনকের প্রত্যেক ধারের দৈর্ঘ্য কত হবে হিসাব করে লিখি।
সমাধানঃ ধরি, ঘনকের প্রত্যেক ধারের দৈর্ঘ্য x সেমি। 432 ঘনসেমি. সমকোণী চৌপলকে সমান আয়তনবিশিষ্ট দুটি ঘনক-এ পরিনত করা হলে, প্রতিটি ঘনকের আয়তন হবে
ঘনকের আয়তন উত্তরঃ নির্ণেয় ঘনকের প্রত্যেক ধারের দৈর্ঘ্য 6 সেমি। |
Koshe dekhi 4 class 10
| Q10. একটি ঘনকের প্রতিটি বাহুকে 50% কমানো হল। মূল ঘনক ও পরিবর্তিত ঘনকের ঘনফলের অনুপাত কি হবে হিসাব করে লিখি।
সমাধানঃ ধরি, ঘনকের বাহুর দৈর্ঘ্য x একক। ∴ ঘনকের ঘনফল ঘনকের প্রতিটি বাহুকে 50% কমানো হলে পরিবর্তিত ঘনকের বাহুর দৈর্ঘ্য হবে ∴ পরিবর্তিত ঘনকের ঘনফল
মূল ঘনক ও পরিবর্তিত ঘনকের ঘনফলের অনুপাত উত্তরঃ নির্ণেয় মূল ঘনক ও পরিবর্তিত ঘনকের ঘনফলের অনুপাত 8:1 |
Koshe dekhi 4 class 10
| Q11. একটি সমকোণী চৌপল আকারের বাক্সের দৈর্ঘ্য, প্রস্থ ও উচ্চতার অনুপাত 3:2:1 এবং উহার আয়তন 384 ঘনসেমি. হলে, বাক্সটির সমগ্র তলের ক্ষেত্রফল কত হবে হিসাব করে লিখি।
সমাধানঃ ধরি, সমকোণী চৌপল আকারের বাক্সের দৈর্ঘ্য (l) = 3x সেমি , প্রস্থ (b) = 2x সেমি ও উচ্চতা (h) = x সেমি। ∴ উহার আয়তন
প্রশ্নানুযায়ী, বা, বা, ∴ দৈর্ঘ্য (l) = 3x = 3×4=12 সেমি , প্রস্থ (b) = 2x =2×4 =8 সেমি ও উচ্চতা (h) = x =4 সেমি।
∴ বাক্সটির সমগ্র তলের ক্ষেত্রফল
উত্তরঃ নির্ণেয় বাক্সটির সমগ্র তলের ক্ষেত্রফল 352 বর্গ সেমি। |
Koshe dekhi 4 class 10
| Q12. একটি চা-এর বাক্সের ভেতরের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 7.5 ডেসিমি, 6 ডেসিমি এবং 5.4 ডেসিমি। চা ভর্তি বাক্সটির ওজন 52 কিগ্রা. 350 গ্রাম। কিন্তু খালি অবস্থায় বাক্সটির ওজন 3.75 কিগ্রা হলে, 1 ঘন ডেসিমি. চা-এর ওজন কত হবে তা হিসাব করে লিখি।
সমাধানঃ প্রদত্ত, চা-এর বাক্সের ভেতরের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 7.5 ডেসিমি, 6 ডেসিমি এবং 5.4 ডেসিমি। চা ভর্তি বাক্সটির ওজন 52 কিগ্রা. 350 গ্রাম =52.350 কিগ্রা। খালি বাক্সটির ওজন 3.75 কিগ্রা। ∴ চা-এর বাক্সের আয়তন বাক্সটির ওজন বাদ দিয়ে শুধুমাত্র 243 ঘন ডেসিমি চা এর ওজন
∴ 1 ঘন ডেসিমি. চা-এর ওজন = 0.2 কিগ্রা = 0.2 × 1000 গ্রাম = 200 গ্রাম। উত্তরঃ নির্ণেয় 1 ঘন ডেসিমি. চা-এর ওজন 200 গ্রাম হবে। |
Koshe dekhi 4 class 10
| Q13. একটি বর্গাকার ভূমিবিশিষ্ট পিতলের প্লেটের দৈর্ঘ্য সমাধানঃ প্রদত্ত, বর্গাকার ভূমিবিশিষ্ট পিতলের প্লেটের দৈর্ঘ্য বেধ 1 মিলিমি. প্লেটটির ওজন 4725 গ্রাম এবং 1 ঘনসেমি. পিতলের ওজন 8.4 গ্রাম। ∴ প্লেটটির আয়তন ∴ প্রশ্নানুসারে, বা, বা, বা,
উত্তরঃ নির্ণেয় x -এর মান 75 |
Koshe dekhi 4 class 10
| Q14. চাঁদমারির রাস্তাটি উঁচু করতে হবে। তাই রাস্তার দুপাশে 30 টি সমান গভীর ও সমান মাপের আয়তঘনাকার গর্ত খুঁড়ে সেই মাটি দিয়ে রাস্তাটি উঁচু করা হয়েছে। যদি প্রতিটি গর্তের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 14 মি. এবং ৪ মি. হয় এবং রাস্তাটি তৈরি করতে মোট 2520 ঘনমিটার মাটি লেগে থাকে, তবে প্রতিটি গর্তের গভীরতা হিসাব করে লিখি।
সমাধানঃ ধরি, প্রতিটি গর্তের গভীরতা h মিটার। প্রদত্ত, প্রতিটি গর্তের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 14 মি. এবং ৪ মি. রাস্তাটি তৈরি করতে মোট 2520 ঘনমিটার মাটি লাগে।
∴ গর্তের আয়তন
প্রশ্নানুসারে,
উত্তরঃ নির্ণেয় প্রতিটি গর্তের গভীরতা 75 সেমি। |
Koshe dekhi 4 class 10
| Q15. ঘনকাকৃতি একটি সম্পূর্ণ জলপূর্ণ চৌবাচ্চা থেকে সমান মাপের 64 বালতি জল তুলে নিলে চৌবাচ্চাটির সমাধানঃ ধরি, সম্পূর্ণ চৌবাচ্চাটিতে জল ধরে 1 অংশ এবং প্রতিটি বালতিতে জল ধরে x লিটার। প্রদত্ত, চৌবাচ্চার একটি ধারের দৈর্ঘ্য = 1.2 মিটার = 1.2×10 =12 ডেসিমি।
∴ চৌবাচ্চাটির আয়তন = 1728 লিটার। [ অর্থাৎ, সম্পূর্ণ চৌবাচ্চাটিতে জল ধরে 1728 লিটার।
প্রশ্নানুসারে, বা, উত্তরঃ নির্ণেয় প্রতিটি বালতিতে 18 লিটার জল ধরে। |
Koshe dekhi 4 class 10
| Q16. এক গ্রোস দেশলাই বাক্সের একটি প্যাকেটের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 2.8 ডেসিমি., 1.5 ডেসিমি. ও 0.9 ডেসিমি. হলে, একটি দেশলাই বাক্সের আয়তন কত হবে হিসাব করি। [এক গ্রোস = 12 ডজন] কিন্তু যদি একটি দেশলাই বাক্সের দৈর্ঘ্য 5 সেমি. এবং প্রস্থ 3.5 সেমি. হয়, তবে তার উচ্চতা কত হবে হিসাব করে লিখি।
সমাধানঃ প্রদত্ত, এক গ্রোস দেশলাই বাক্সের একটি প্যাকেটের দৈর্ঘ্য (L) = 2.8 ডেসিমি. = 28 সেমি প্রস্থ (B) = 1.5 ডেসিমি.= 15 সেমি ও উচ্চতা (H) = 0.9 ডেসিমি. = 9 সেমি।
∴ দেশলাই বাক্সের প্যাকেটের আয়তন
∴ একটি দেশলাই বাক্সের আয়তন
ধরি, একটি দেশলাই বাক্সের উচ্চতা h সেমি। প্রদত্ত, দেশলাই বাক্সের দৈর্ঘ্য (l) = 5 সেমি. এবং প্রস্থ (b) = 3.5 সেমি. বা, বা, উত্তরঃ নির্ণেয় একটি দেশলাই বাক্সের আয়তন 26.25 ঘনসেমি এবং দেশলাই বাক্সের উচ্চতা 1.5 সেমি । |
Koshe dekhi 4 class 10
| Q17. 2.1 মিটার দীর্ঘ, 1.5 মিটার প্রশস্ত একটি আয়তঘনকাকার চৌবাচ্চার অর্ধেক জলপূর্ণ আছে। ওই চৌবাচ্চায় আরও 630 লিটার জল ঢাললে জলের গভীরতা কতটা বৃদ্ধি পাবে হিসাব করে লিখি।
সমাধানঃ ধরি, আয়তঘনকাকার চৌবাচ্চায় জলের গভীরতা h ডেসিমি বৃদ্ধি পাবে। প্রদত্ত, চৌবাচ্চাটির দৈর্ঘ্য (l) = 2.1 মিটার = 21 ডেসিমি. এবং প্রস্থ (b) = 1.5 মিটার = 15 ডেসিমি. 630 লিটার = 630 ঘন ডেসিমি। [
প্রশ্নানুসারে, \( lbh=630 \) বা, \( 21\times 15\times h=630 \) বা, \( h=\frac{630}{21\times 15} \) \( \therefore h=2 \) উত্তরঃ নির্ণেয় আয়তঘনকাকার চৌবাচ্চায় জলের গভীরতা 2 ডেসিমি বৃদ্ধি পাবে। |
Koshe dekhi 4 class 10
| Q18. গ্রামের আয়তক্ষেত্রাকার মাঠের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 20 মিটার এবং 15 মিটার। ওই মাঠের ভিতরে চারটি কোনে পিলার বসানোর জন্য 4 মিটার দৈর্ঘ্য বিশিষ্ট চারটি ঘনকাকৃতি গর্ত কেটে অপসারিত মাটি অবশিষ্ট জমির ওপর ছড়িয়ে দেওয়া হল। মাঠের তলের উচ্চতা কতটা বৃদ্ধি পেল হিসাব করে লিখি।
সমাধানঃ ধরি, মাঠের তলের উচ্চতা h মিটার বৃদ্ধি পাবে। প্রদত্ত, আয়তক্ষেত্রাকার মাঠের দৈর্ঘ্য = 20 মিটার ও প্রস্থ = 15 মিটার।
∴ মাঠটির ক্ষেত্রফল
4 টি পিলার বসানোর জন্য ব্যবহৃত জমির ক্ষেত্রফল অবশিষ্ট জমির ক্ষেত্রফল
4 টি পিলার বসানোর জন্য অপসারিত মাটির আয়তন
প্রশ্নানুসারে, বা,
উত্তরঃ নির্ণেয় মাঠের তলের উচ্চতা |
Koshe dekhi 4 class 10
| Q19. 48 মিটার লম্বা এবং 31.5 মিটার চওড়া একখন্ড নীচু জমিকে 6.5 ডেসিমি. উঁচু করার জন্য ঠিক করা হয়েছে পাশের 27 মিটার লম্বা এবং 18.2 মিটার চওড়া একটি জমি গর্ত করে মাটি তোলা হবে। গর্তটি কত মিটার গভীর করতে হবে হিসাব করে লিখি।
সমাধানঃ প্রদত্ত, নীচু জমির দৈর্ঘ্য = 48 মিটার, প্রস্থ = 31.5 মিটার উচ্চতা = 6.5 ডেসিমি.
∴ আয়তন = দৈর্ঘ্য × প্রস্থ × উচ্চতা
গর্ত খোঁড়া জমির দৈর্ঘ্য = 27 মিটার এবং প্রস্থ = 18.2 মিটার।
ধরি, গর্তটি h মিটার গভীর করতে হবে।
∴ তোলা মাটির পরিমান
প্রশ্নানুসারে, বা, উত্তরঃ নির্ণেয় গর্তটি 2 মিটার গভীর করতে হবে। |
Koshe dekhi 4 class 10
| Q20. বাড়ির তিনটি কেরোসিন তেলের ড্রামে যথাক্রমে 800 লিটার, 725 লিটার এবং 575 লিটার তেল ছিল। ওই তিনটি ড্রামের তেল একটি আয়তঘনাকার পাত্রে ঢালা হল এবং এতে পাত্রে তেলের গভীরতা 7 ডেসিমি. হল। ওই আয়তঘনাকার পাত্রের দৈর্ঘ্য ও প্রস্থের অনুপাত 4:3 হলে, পাত্রের দৈর্ঘ্য ও প্রস্থ হিসাব করে লিখি।
যদি ওই আয়তঘনাকার পাত্রের গভীরতা 5 ডেসিমিটার হতো, তবে 1620 লিটার তেল ঐ পাত্রে রাখা যেত কিনা হিসাব করে দেখি। সমাধানঃ তিনটি কেরোসিন তেলের ড্রামে মোট তেলের পরিমান
ধরি, আয়তঘনাকার পাত্রের দৈর্ঘ্য 4a ডেসিমি. ও প্রস্থ 3a ডেসিমি.। পাত্রে তেলের গভীরতা 7 ডেসিমি.।
আয়তঘনাকার পাত্রে তেলের পরিমান
প্রশ্নানুসারে, বা, বা, আয়তঘনাকার পাত্রের দৈর্ঘ্য ও প্রস্থ উত্তরঃ নির্ণেয় আয়তঘনাকার পাত্রের দৈর্ঘ্য আবার, যদি ওই আয়তঘনাকার পাত্রের গভীরতা 5 ডেসিমিটার হতো, তবে পাত্রটির আয়তন হতো যেহেতু |
Koshe dekhi 4 class 10
| Q21. আমাদের তিনতলা ফ্লাটের তিনটি পরিবারের দৈনিক জলের চাহিদা যথাক্রমে 1200 লিটার, 1050 লিটার এবং 950 লিটার। এই চাহিদা মেটানোর পরও চাহিদার 25% জল মজুদ থাকে এমন একটি ট্যাঙ্ক বসানোর জন্য মাত্র 2.5 মি. দীর্ঘ এবং 1.6 মিটার চওড়া একটি জায়গা পাওয়া গেছে। ট্যাঙ্কটি কত মিটার গভীর করতে হবে হিসাব করে লিখি। জায়গাটি যদি প্রস্থের দিকে আরও 4 ডেসিমি. বেশি হত, তবে ট্যাঙ্কটি কতটা গভীর করতে হতো, তা হিসাব করে লিখি।
সমাধানঃ তিনটি পরিবারের দৈনিক মোট জলের চাহিদা
চাহিদা মেটানোর পর জল মজুদ থাকে
ধরি, ট্যাঙ্কটিকে d মিটার গভীর করতে হবে।
প্রদত্ত, ট্যাঙ্কটির দৈর্ঘ্য
প্রশ্নানুযায়ী, বা, উত্তরঃ নির্ণেয় ট্যাঙ্কটিকে 1 মিটার গভীর করতে হবে। জায়গাটি যদি প্রস্থের দিকে আরও 4 ডেসিমি. বেশি হত, তবে প্রস্থ হতো ধরি, ট্যাঙ্কটি এবার h মিটার গভীর করতে হতো। প্রশ্নানুসারে, বা, উত্তরঃ নির্ণেয় ট্যাঙ্কটিকে এবার |
Koshe dekhi 4 class 10
| Q22. 5 সেমি. পুরু কাঠের তক্তায় তৈরি ঢাকনাসহ একটি কাঠের বাক্সের ওজন 115.5 কিগ্রা। কিন্তু চাল ভর্তি বাক্সটির ওজন 880.5 কিগ্রা। বাক্সটির ভিতরের দিকের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 12 ডেসিমি. এবং 8.5 ডেসিমি. এবং এক ঘন ডেসিমি. চালের ওজন 1.5 কিগ্রা। বাক্সটির ভিতরের উচ্চতা কত হিসাব করে লিখি। প্রতি বর্গ ডেসিমি. 1.50 টাকা হিসাবে বাক্সটির বাইরের চারিপাশ রং করতে কত খরচ পড়বে হিসাব করে লিখি।
সমাধানঃ প্রথম অংশ : প্রদত্ত, কাঠের বাক্সের ওজন 115.5 কিগ্রা, চাল ভর্তি বাক্সটির ওজন 880.5 কিগ্রা। ∴ শুধু চালের ওজন
1.5 কিগ্রা চালের আয়তন
ধরি, বাক্সটির ভিতরের দিকের উচ্চতা
প্রদত্ত, বাক্সটির ভিতরের দিকের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 12 ডেসিমি. এবং 8.5 ডেসিমি.
প্রশ্নানুসারে, বা, সুতরাং, নির্ণেয় বাক্সটির উচ্চতা 5 ডেসিমি. দ্বিতীয় অংশ : যেহেতু বাক্সটি 5 সেমি. অর্থাৎ, 0.5 ডেসিমি. পুরু। সুতরাং, বাক্সটির বাইরের দিকের পরিমাপ হলো নিম্নরূপ : দৈর্ঘ্য (l) = [12 + (2×0.5)] অর্থাৎ, 13 ডেসিমি. প্রস্থ (b) = [8.5 + (2×0.5)] অর্থাৎ, 9.5 ডেসিমি. উচ্চতা (h) = [5 + (2×0.5)] অর্থাৎ, 6 ডেসিমি. ∴ বাক্সটির সমগ্রতলের ক্ষেত্রফল = 2(l×b + b×h + h×l) = 2(13×9.5 + 9.5×6 + 6×13) বর্গ ডেসিমি. = 2(123.5 + 57 + 78) বর্গ ডেসিমি. = 2×258.5 বর্গ ডেসিমি. = 517 বর্গ ডেসিমি. এখন, প্রতি বর্গ ডেসিমি. 1.50 টাকা হিসাবে বাক্সটির বাইরের চারিপাশ রং করতে মোট খরচ পড়বে = Rs. 1.5 × 517 অর্থাৎ, Rs. 775.50 উত্তরঃ নির্ণেয় বাক্সটির উচ্চতা 5 ডেসিমি. এবং বাক্সটির বাইরের চারিপাশ রং করতে মোট খরচ পড়বে 775.50 টাকা। |
Koshe dekhi 4 class 10
| Q23. 20 মি. দীর্ঘ এবং 18.5 মি. চওড়া একটি আয়তঘনাকার পুকুরে 3.2 মি. গভীর জল আছে। ঘন্টায় 160 কিলোলিটার জলসেচ করতে পারে এমন একটি পাম্প দিয়ে কতক্ষণে পুকুরটির সমস্ত জলসেচ করা যাবে হিসাব করে লিখি। ওই জল যদি 59.2 মিটার দীর্ঘ এবং 40 মিটার চওড়া একটি আল দেওয়া ধান ক্ষেতে ফেলা হয়, তবে সেই জমিতে জলের গভীরতা কত হবে হিসাব করে লিখি । [1 ঘন মিটার = 1 কিলোলিটার]
সমাধানঃ প্রদত্ত, পুকুরের দৈর্ঘ্য প্রস্থ ও জলের উচ্চতা
∴ পুকুরে মোট জলের পরিমান
পাম্পটি
ধরি, ধান ক্ষেতের জমিতে জলের গভীরতা h মিটার। ধান ক্ষেতের দৈর্ঘ্য প্রস্থ
প্রশ্নানুসারে, বা, বা, উত্তরঃ নির্ণেয় পাম্পটি দিয়ে |
Koshe dekhi 4 class 10
| Q24. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.) :
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) : (i) একটি সমকোণী চৌপলাকৃতি বাক্সের ভিতরের আয়তন 440 ঘন সেমি. এবং ভিতরের ভূমিতলের ক্ষেত্রফল 88 বর্গ সেমি.। বাক্সর্টির ভিতরের উচ্চতা (a) 4 সেমি. (b) 5 সেমি. (c) 3 সেমি. (d) 6 সেমি. সমাধানঃ ধরি, বাক্সর্টির ভিতরের উচ্চতা h সেমি। প্রদত্ত, সমকোণী চৌপলাকৃতি বাক্সের ভিতরের আয়তন 440 ঘন সেমি. এবং ভিতরের ভূমিতলের ক্ষেত্রফল 88 বর্গ সেমি.। আমরা জানি, সমকোণী চৌপলাকৃতি বাক্সের আয়তন = ভূমিতলের ক্ষেত্রফল × উচ্চতা অর্থাৎ, বা, উত্তরঃ নির্ণেয় বাক্সর্টির ভিতরের উচ্চতা 5 সেমি। |
Koshe dekhi 4 class 10
| Q24. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.) :
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) : (ii) একটি আয়তঘনাকার গর্তের দৈর্ঘ্য 40 মি., প্রস্থ 12 মি. এবং গভীরতা 16 মি.। ওই গর্তের মধ্যে 5 মি. দৈর্ঘ্য, 4 মি. প্রস্থ এবং 2 মি. পুরু তক্তা রাখা যাবে (a) 190 টি (b) 192 টি (c) 184 টি (d) 180 টি সমাধানঃ প্রদত্ত, আয়তঘনাকার গর্তের দৈর্ঘ্য 40 মি., প্রস্থ 12 মি. এবং গভীরতা 16 মি.। ∴ গর্তের আয়তন
তক্তার দৈর্ঘ্য 5 মি. , প্রস্থ 4 মি. এবং পুরু 2 মি.
∴ তক্তার আয়তন ∴ ওই গর্তের ভিতর তক্তা রাখা যাবে উত্তরঃ নির্ণেয় তক্তা সংখ্যা 192 টি। |
Koshe dekhi 4 class 10
| Q24. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.) :
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) : (iii) একটি ঘনকের পার্শ্বতলের ক্ষেত্রফল 256 বর্গ মিটার। ঘনকটির আয়তন (a) 64 ঘন মি. (b) 216 ঘন মি. (c) 256 ঘন মি. (d) 512 ঘন মি. সমাধানঃ প্রদত্ত, ঘনকের পার্শ্বতলের ক্ষেত্রফল 256 বর্গ মিটার। ∴ প্রতিটি তলের ক্ষেত্রফল
∴ ঘনকের বাহুর দৈর্ঘ্য ∴ ঘনকটির আয়তন উত্তরঃ নির্ণেয় ঘনকটির আয়তন 512 ঘন মিটার। |
Koshe dekhi 4 class 10
| Q24. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.) :
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) : (iv) দুটি ঘনকের আয়তনের অনুপাত 1 : 27 হলে, ঘনক দুটির সমগ্রতলের ক্ষেত্রফলের অনুপাত (a) 1 : 3 (b) 1 : 8 (c) 1 : 9 (d) 1 : 18 সমাধানঃ ধরি, ঘনক দুটির বাহুর দৈর্ঘ্য যথাক্রমে, a একক ও b একক।
প্রশ্নানুসারে, বা, বা, বা,
ঘনক দুটির সমগ্রতলের ক্ষেত্রফলের অনুপাত
উত্তরঃ নির্ণেয় ঘনক দুটির সমগ্রতলের ক্ষেত্রফলের অনুপাত 1:9 |
Koshe dekhi 4 class 10
| Q24. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.) :
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) : (v) একটি ঘনকের সমগ্রতলের ক্ষেত্রফল s বর্গ একক এবং কর্ণের দৈর্ঘ্য d একক হলে, s এবং d এর সম্পর্ক (a) (b) (c) (d) সমাধানঃ ধরি, ঘনকের বাহুর দৈর্ঘ্য a একক। ∴ ঘনকের সমগ্রতলের ক্ষেত্রফল বা,
∴ কর্ণের দৈর্ঘ্য বা, বা, বা, বা, উত্তরঃ নির্ণেয় s এবং d এর সম্পর্ক |
Koshe dekhi 4 class 10
| (B) নিচের বিবৃতিগুলি সত্য না মিথ্যা লিখি :
(i) একটি ঘনকের প্রতিটি ধারের দৈর্ঘ্য দ্বিগুন হলে, ঘনকটির আয়তন প্রথম ঘনকের 4 গুন হবে। সমাধানঃ ধরি, পূর্বে ঘনকটির বাহুর দৈর্ঘ্য ছিল ∴ পূর্বে ঘনকটির আয়তন ছিল বর্তমানে ঘনকটির বাহুর দৈর্ঘ্য ∴ এখন আয়তন হবে ∴ ঘনকের প্রতিটি ধারের দৈর্ঘ্য দ্বিগুন হলে, ঘনকটির আয়তন প্রথম ঘনকের 8 গুন হবে। উত্তরঃ বিবৃতিটি মিথ্যা। |
Koshe dekhi 4 class 10
| (B) নিচের বিবৃতিগুলি সত্য না মিথ্যা লিখি :
(ii) বর্ষার সময় 2 হেক্টর জমিতে বৃষ্টিপাত 5 সেমি. উচ্চতার হলে, বৃষ্টির জলের আয়তন 1000 ঘন মিটার। সমাধানঃ 1 হেক্টর = 100 আর ∴ 2 হেক্টর = 200 আর = 200 × 100 বর্গ মি. 5 সেমি. = 0.05 মিটার। ∴ বৃষ্টির জলের আয়তন = 200 × 100 × 0.05 ঘন মিটার = 1000 ঘন মিটার। উত্তরঃ বিবৃতিটি সত্য। |
Koshe dekhi 4 class 10
| (C) শূন্যস্থান পূরণ করি :
(i) একটি সমকোণী চৌপলের কর্ণের সংখ্যা _________ টি। উত্তরঃ 4 টি।
(ii) একটি ঘনকের একটি তলের কর্ণের দৈর্ঘ্য = ______ × একটি ধারের দৈর্ঘ্য। উত্তরঃ
(iii) সমকোণী চৌপলের দৈর্ঘ্য, প্রস্থ ও উচ্চতা সমান হলে সেই ঘনবস্তুর বিশেষ নাম _______। উত্তরঃ ঘনক। |
Koshe dekhi 4 class 10
| Q25. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) :
(i) একটি আয়তঘনের তল সংখ্যা = x, ধার সংখ্যা = y, শীর্ষবিন্দুর সংখ্যা = z এবং কর্ণের সংখ্যা = p হলে, x – y + z + p এর মান কত তা লিখি। সমাধানঃ আমরা জানি, আয়তঘনের তল সংখ্যা (x) = 6, ধার সংখ্যা (y) = 12, শীর্ষবিন্দুর সংখ্যা (z) = 8 এবং কর্ণের সংখ্যা (p) = 4 ∴ x – y + z + p = 6 − 12 + 8 + 4 = 6 উত্তরঃ নির্ণেয় x – y + z + p এর মান 6 |
Koshe dekhi 4 class 10
| Q25. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) :
(ii) দুটি আয়তঘনের মাত্রাগুলির দৈর্ঘ্য যথাক্রমে 4, 6, 4 একক এবং 8, (2h – 1), 2 একক। যদি আয়তঘন দুটির ঘনফল সমান হয়, তাহলে h এর মান কত তা লিখি। সমাধানঃ প্রথম আয়তঘনকের আয়তন
দ্বিতীয় আয়তঘনকের আয়তন প্রশ্নানুসারে, প্রথম আয়তঘনকের আয়তন = দ্বিতীয় আয়তঘনকের আয়তন বা, বা, বা, উত্তরঃ নির্ণেয় h এর মান |
Koshe dekhi 4 class 10
| Q25. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) :
(iii) একটি ঘনকের প্রত্যেকটি ধারের দৈর্ঘ্য 50% বৃদ্ধি পেলে, ঘনকর্টির সমগ্রতলের ক্ষেত্রফল শতকরা কত বৃদ্ধি হবে তা হিসাব করে লিখি। সমাধানঃ ধরি, পূর্বে ঘনকের প্রত্যেকটি ধারের দৈর্ঘ্য ছিল a একক। ∴ ঘনকর্টির সমগ্রতলের ক্ষেত্রফল ছিল
বর্তমানে ঘনকের প্রত্যেকটি ধারের দৈর্ঘ্য ∴ বর্তমানে ঘনকর্টির সমগ্রতলের ক্ষেত্রফল
ঘনকর্টির সমগ্রতলের ক্ষেত্রফল বৃদ্ধি পেয়েছে ∴ ক্ষেত্রফলের শতকরা বৃদ্ধির হার উত্তরঃ নির্ণেয় ঘনকর্টির সমগ্রতলের ক্ষেত্রফল শতকরা 125 ভাগ বৃদ্ধি পাবে। |
Koshe dekhi 4 class 10
| Q25. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) :
(iv) তিনটি নিরেট ঘনক যাদের প্রত্যেকটি ধারের দৈর্ঘ্য যথাক্রমে 3 সেমি., 4 সেমি. এবং 5 সেমি.। ঘনক তিনটিকে গলিয়ে একটি নতুন নিরেট ঘনক তৈরি করা হলো। নতুন ঘনকটির একটি ধারের দৈর্ঘ্য কত হবে তা লিখি। সমাধানঃ প্রদত্ত, প্রথম ঘনকের বাহুর দৈর্ঘ্য = 3 সেমি. ∴ প্রথম ঘনকের আয়তন
দ্বিতীয় ঘনকের বাহুর দৈর্ঘ্য = 4 সেমি. ∴ দ্বিতীয় ঘনকের আয়তন
তৃতীয় ঘনকের বাহুর দৈর্ঘ্য = 5 সেমি. ∴ তৃতীয় ঘনকের আয়তন
ধরি, নতুন ঘনকের বাহুর দৈর্ঘ্য = a সেমি. ∴ নতুন ঘনকের আয়তন
প্রশ্নানুসারে, বা, উত্তরঃ নির্ণেয় নতুন ঘনকটির একটি ধারের দৈর্ঘ্য 6 সেমি. |
Koshe dekhi 4 class 10
| Q25. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) :
(v) একটি ঘরের দুটি সংলগ্ন দেওয়ালের দৈর্ঘ্য যথাক্রমে 12 মি. এবং ৪ মি.। ঘরটির উচ্চতা 4 মি. হলে, ঘরটির মেঝের ক্ষেত্রফল কত তা হিসাব করে লিখি। সমাধানঃ প্রদত্ত, মেঝের দৈর্ঘ্য = 12 মিটার, ও প্রস্থ = 8 মিটার। ∴ ঘরটির মেঝের ক্ষেত্রফল = 12 × 8 = 96 বর্গ মিটার। উত্তরঃ নির্ণেয় ঘরটির মেঝের ক্ষেত্রফল 96 বর্গ মিটার। |
Thanku sir 🙏🙏🙏 this is very helpful
thank u so much
Thank you so much sir
most welcome
Hare Krishna
No
Tnx sir many many so much
Thank you sir
most welcome.