Koshe dekhi 18.4 class 10

Table of Contents

Koshe dekhi 18.4 class 10

জ্যামিতি : সদৃশ্যতা : কষে দেখি – 18.4

Q1. ΔABC -এর ∠ABC = 90° এবং BD ⊥ AC; যদি BD = 8 সেমি. এবং AD = 5 সেমি. হয়, তবে CD -এর দৈর্ঘ্য হিসাব করে লিখি।

উত্তরঃ

CD -এর দৈর্ঘ্য 12.8 সেমি.

সমাধানঃ

সদৃশ্যতা

যেহেতু, সমকোণী ΔABC -এর সমকৌণিক বিন্দু B থেকে অতিভুজ AC বাহুর উপর BD লম্ব।

অতএব, ΔABD ∼ ΔBDC

সদৃশ্যকোণী ΔABD ও ΔBDC -এ

∠BAD = ∠DBC ; ∠ADB = ∠BDC এবং ∠ABD = ∠BCD

অর্থ্যাৎ, $\small \frac{BD}{CD}=\frac{AB}{BC}=\frac{AD}{BD}$ [সদৃশ্যকোণী ত্রিভুজের অনুরূপ কোনগুলির বিপরীত বাহুগুলি সমানুপাতী হয়]

এখন, $\small \frac{BD}{CD}=\frac{AD}{BD}$ থেকে পাই-

$\small \frac{8\; cm.}{CD}=\frac{5\; cm.}{8\; cm.}$ [মান বসিয়ে পাই]

বা, $\small \frac{8\; cm.}{CD}=\frac{5}{8}$

বা, $\small CD=\frac{8\times 8}{5}\; cm.$
বা, $\small CD=\frac{64}{5}\; cm.$

$\small \therefore CD=12.8\; cm.$ (উত্তর)

জ্যামিতি : সদৃশ্যতা : কষে দেখি – 18.4

Q2. ABC একটি সমকোণী ত্রিভুজ যার ∠B সমকোণ এবং BD ⊥ AC; যদি AD = 4 সেমি. এবং CD = 16 সেমি. হয়, তবে BD ও AB -এর দৈর্ঘ্য হিসাব করে লিখি।

উত্তরঃ

BD -এর দৈর্ঘ্য 8 সেমি. ও AB -এর দৈর্ঘ্য $\small {\color{Blue} 4\sqrt{5}}$ সেমি.

সমাধানঃ

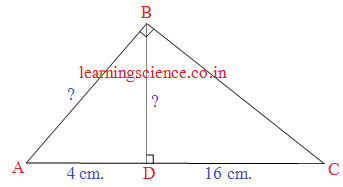
সদৃশ্যতা

যেহেতু, সমকোণী ΔABC -এর সমকৌণিক বিন্দু B থেকে অতিভুজ AC বাহুর উপর BD লম্ব।

অতএব, ΔABD ∼ ΔBDC

সদৃশ্যকোণী ΔABD ও ΔBDC -এ

∠BAD = ∠DBC ; ∠ADB = ∠BDC এবং ∠ABD = ∠BCD

এখন, $\small \frac{BD}{CD}=\frac{AD}{BD}$ থেকে পাই-

$\small \frac{BD}{16\; cm.}=\frac{4\; cm.}{BD}$ [মান বসিয়ে পাই]

বা, $\small BD^{2}=16\times 4 \; cm^{2}$

বা, $\small BD=\sqrt{64} \; cm.$

$\small \therefore BD=8\; cm.$ (উত্তর)

আবার, সমকোণী ΔABD থেকে পাই –

(AB)² = (AD)² + (BD)² [পিথাগোরাসের সূত্রানুসারে]

এখন, মান বসিয়ে পাই-

বা, (AB)² = (4)² + (8)²

বা, (AB)² = 16 + 64

বা, (AB)² = 80

বা, $\small AB=\sqrt{80}$

বা, $\small AB=\sqrt{4\times 4\times 5}$

$\small \therefore AB=4\sqrt{5}\; cm.$ (উত্তর)

জ্যামিতি : সদৃশ্যতা : কষে দেখি – 18.4

Q3. O কেন্দ্রবিশিষ্ট একটি বৃত্তের AB একটি ব্যাস। P বৃত্তের উপর যে-কোনো একটি বিন্দু। A ও B বিন্দুতে অঙ্কিত স্পর্শক দুটিকে P বিন্দুতে অঙ্কিত স্পর্শকটি যথাক্রমে Q ও R বিন্দুতে ছেদ করেছে। যদি বৃত্তের ব্যাসার্ধ r হয়, প্রমাণ করি যে, PQ.PR = r².

উত্তরঃ

সদৃশ্যতা

ধরি, O কেন্দ্রীয় বৃত্তের AB হলো একটি ব্যাস। বৃত্তটির উপর P যে কোনো একটি বিন্দু এবং P বিন্দু থেকে অঙ্কিত A ও B বিন্দুগামী স্পর্শক দুটিকে যথাক্রমে Q ও R বিন্দুতে ছেদ করে।

প্রমাণ করতে হবে যে, PQ•PR = r² (যেখানে, r = বৃত্তের ব্যাসার্ধ)

অঙ্কনঃ O, P; O, R; ও O, Q যুক্ত করা হলো।

প্রমাণঃ যেহেতু, O কেন্দ্রীয় বৃত্তের বহিঃস্থ বিন্দু Q থেকে দুটি স্পর্শক হলো PQ ও AQ

অতএব, PQ ও AQ স্পর্শক দুটি বৃত্তের কেন্দ্রে সমান কোণ উৎপন্ন করবে অর্থ্যাৎ, ∠AOQ = ∠POQ ……..(i)

একইভাবে, প্রমাণ করা যায় যে,

∠BOR = ∠POR …….(ii)

এখন, (i) ও (ii) নং সমীকরণ যোগ করে পাই –

∠AOQ + ∠BOR = ∠POQ + ∠POR ……….(iii)

আবার,
যেহেতু, ∠AOQ + ∠BOR + ∠POQ + ∠POR = 180°

বা, ∠POQ + ∠POR + ∠POQ + ∠POR = 180° [(iii) নং সমীকরণ ব্যবহার করে]

বা, 2 (∠POQ + ∠POR) = 180°

বা, ∠POQ + ∠POR = $\small \frac{180^{\circ}}{2}$

∴ ∠ROQ = 90°

এখন, যেহেতু ΔROQ -এর ∠ROQ = 90° এবং সমকৌণিক বিন্দু O থেকে অতিভুজ QR এর উপর OP লম্ব। [OP ⊥ QR, কারণ QR হলো বৃত্তের স্পর্শক এবং OP হলো স্পর্শবিন্দুগামী ব্যাসার্ধ]

∴ ΔOPR ∼ ΔOPQ

সদৃশ্যকোণী ΔOPR ও ΔOPQ -এ

সুতরাং, ∠OPQ = ∠OPR; ∠POQ = ∠PRO; এবং ∠OQP = ∠POR

অতএব, $\small \frac{OQ}{OR}=\frac{PQ}{OP}=\frac{OP}{PR}$ [সদৃশ্যকোণী ত্রিভুজের অনুরূপ কোনগুলির বিপরীত বাহুগুলি সমানুপাতী হয়]

এখন, $\small \frac{PQ}{OP}=\frac{OP}{PR}$ থেকে পাই-

বা, $\small PQ\cdot PR=(OP)^{2}$

$\small \therefore PQ\cdot PR=r^{2}$ [যেহেতু, OP = r, বৃত্তের ব্যাসার্ধ] (প্রমাণিত)

জ্যামিতি : সদৃশ্যতা : কষে দেখি – 18.4

Q4. AB -কে ব্যাস করে একটি অর্ধবৃত্ত অঙ্কন করেছি। AB -এর উপর যে-কোনো বিন্দু C থেকে AB -এর উপর লম্ব অঙ্কন করেছি যা অর্ধবৃত্তকে D বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, CD, AC ও BC -এর মধ্যসমানুপাতী।

সমাধানঃ

সদৃশ্যতা

ধরি, অর্ধবৃত্তের AB হলো ব্যাস এবং C বিন্দু AB -এর উপর অবস্থিত যে কোনো একটি বিন্দু। C বিন্দু থেকে AB -এর উপর অঙ্কিত লম্ব অর্ধবৃত্তকে D বিন্দুতে ছেদ করে।

প্রমাণ করতে হবে যে, AC ও BC -এর মধ্যসমানুপাতী হলো CD অর্থ্যাৎ, $\small \left (CD \right )^{2}=AC\cdot BC$

অঙ্কনঃ A, D ও B, C যুক্ত করা হলো।

প্রমাণঃ যেহেতু, AB হলো ব্যাস এবং D হলো অর্ধবৃত্তের উপর অবস্থিত যে কোনো একটি বিন্দু।

∠ADB = 90° (অর্ধবৃত্তস্থ কোণ)

এখন, যেহেতু সমকোণী ত্রিভুজ ADB -এর সমকৌণিক বিন্দু D থেকে অতিভুজ AB -এর উপর CD লম্ব।

ΔADC ∼ ΔDBC

সদৃশ্যকোণী ΔADC ও ΔDBC -এ

∠DAC = ∠BDC ; ∠ACD = ∠DCB এবং ∠ADC = ∠DBC

সুতরাং, $\small \frac{AC}{CD}=\frac{CD}{BC}$ [সদৃশ্যকোণী ত্রিভুজের অনুরূপ কোনগুলির বিপরীত বাহুগুলি সমানুপাতী হয়]

∴ $\small \left (CD \right )^{2}=AC\cdot BC$ (প্রমাণিত)

জ্যামিতি : সদৃশ্যতা : কষে দেখি – 18.4

Q5. সমকোণী ত্রিভুজ ABC -এর ∠A সমকোণ। অতিভুজ BC -এর উপর লম্ব AD হলে, প্রমাণ করি যে, $\small {\color{Blue} \frac{\Delta ABC}{\Delta ACD}=\frac{BC^{2}}{AC^{2}}}$ .

সমাধানঃ

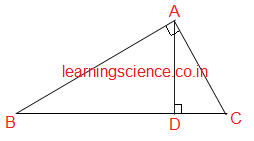
সদৃশ্যতা

ধরি, সমকোণী ΔABC -এর সমকৌণিক বিন্দু A থেকে অতিভুজ BC -এর উপর AD লম্ব।

প্রমাণ করতে হবে যে, $\small \frac{\Delta ABC}{\Delta ACD}=\frac{BC^{2}}{AC^{2}}$

প্রমাণঃ যেহেতু, সমকোণী ΔABC -এর সমকৌণিক বিন্দু A থেকে অতিভুজ BC বাহুর উপর AD লম্ব।

ΔABC ∼ ΔADC

সদৃশ্যকোণী ΔABC ও ΔADC -এ

∠ABC = ∠DAC ; ∠BAC = ∠ADC এবং ∠ACB = ∠ACD

সুতরাং, $\small \frac{BC}{AC}=\frac{AC}{CD}$ [সদৃশ্যকোণী ত্রিভুজের অনুরূপ কোনগুলির বিপরীত বাহুগুলি সমানুপাতী হয়]

বা, $\small \left (AC \right )^{2}=BC\cdot CD$

বা, $\small CD=\frac{\left (AC \right )^{2}}{BC}$ ……..(i)

∴ ΔABC -এর ক্ষেত্রফল $\small =\frac{1}{2}\times BC\times AD$ বর্গ একক ……..(ii)

এবং ΔACD -এর ক্ষেত্রফল $\small =\frac{1}{2}\times CD\times AD$ বর্গ একক ……..(iii)

(ii) ও (iii) নং সমীকরণ দুটিকে ভাগ করে পাই-

$\small \frac{\Delta ABC}{\Delta ACD}=\frac{\frac{1}{2}\times BC\times AD}{\frac{1}{2}\times CD\times AD}$

বা, $\small \frac{\Delta ABC}{\Delta ACD}=\frac{BC}{CD}$

CD -এর মান বসিয়ে পাই-

বা, $\small \frac{\Delta ABC}{\Delta ACD}=\frac{BC}{\frac{\left ( AC \right )^{2}}{BC}}$

$\small \therefore \frac{\Delta ABC}{\Delta ACD}=\frac{\left (BC \right )^{2}}{\left (AC \right )^{2}}$ (প্রমাণিত)

Support Me

If you like my work then you can Support me by contributing a small amount which will help me a lot to grow my channel. It’s a request to all of you. You can donate me through phone pay / Paytm/ Gpay on this number 7980608289 or by the link below :

জ্যামিতি : সদৃশ্যতা : কষে দেখি – 18.4

Q6. O কেন্দ্রীয় বৃত্তের AB ব্যাস। A বিন্দু দিয়ে অঙ্কিত একটি সরলরেখা বৃত্তকে C বিন্দুতে এবং B বিন্দুতে অঙ্কিত স্পর্শককে D বিন্দুতে ছেদ করে। প্রমাণ করি যে,

(i) BD² = AD.DC

(ii) যে-কোনো সরলরেখার জন্য AC এবং AD দ্বারা গঠিত আয়তক্ষেত্রের ক্ষেত্রফল সর্বদা সমান।

সমাধানঃ

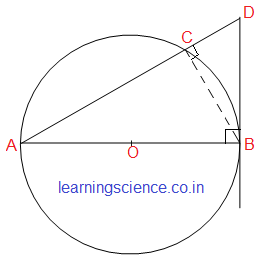
সদৃশ্যতা

O কেন্দ্রীয় বৃত্তের AB হলো একটি ব্যাস। A বিন্দু দিয়ে অঙ্কিত একটি সরলরেখা বৃত্তকে C বিন্দুতে এবং B বিন্দুগামী স্পর্শককে D বিন্দুতে ছেদ করে।

প্রমাণ করতে হবে যে, (i) BD² = AD.DC

(ii) যে-কোনো সরলরেখার জন্য AC এবং AD দ্বারা গঠিত আয়তক্ষেত্রের ক্ষেত্রফল সর্বদা সমান অর্থ্যাৎ, AD.AC = AB²

অঙ্কনঃ B, C যুক্ত করা হলো।

প্রমাণঃ যেহেতু, BD হলো স্পর্শক যার স্পর্শবিন্দু B এবং AB হলো স্পর্শবিন্দুগামী (অর্থ্যাৎ, B) ব্যাস।

∴ BC ⊥ BD

সুতরাং, ABD হলো সমকোণী ত্রিভুজ যার ∠ABD = 90°

আবার, ∠ACB = 90° (অর্ধবৃত্তস্থ কোণ)

এখন, যেহেতু সমকোণী ΔABD -এর সমকৌণিক বিন্দু B থেকে অতিভুজ AD -এর উপর BC লম্ব।

∴ ΔABD ∼ ΔBCD ও ΔABD ∼ ΔABC

সদৃশ্যকোণী ΔABD ও ΔBCD -এ

∠BAD = ∠DBC ; ∠ADB = ∠BCD এবং ∠ADB = ∠BDC

সুতরাং, $\small \frac{BD}{DC}=\frac{AD}{BD}=\frac{AB}{BC}$ [সদৃশ্যকোণী ত্রিভুজের অনুরূপ কোনগুলির বিপরীত বাহুগুলি সমানুপাতী হয়]

এখন, $\small \frac{BD}{DC}=\frac{AD}{BD}$ থেকে পাই-

$\small \left ( BD \right )^{2}=AD\cdot DC$ ……(i) (প্রমাণিত)

সদৃশ্যকোণী ΔABD ও ΔABC -এ

∠ABD = ∠ACB ; ∠ADB = ∠ABC এবং ∠DAB = ∠CAB

সুতরাং, $\small \frac{AD}{AB}=\frac{AB}{AC}=\frac{DB}{BC}$ [সদৃশ্যকোণী ত্রিভুজের অনুরূপ কোনগুলির বিপরীত বাহুগুলি সমানুপাতী হয়]

এখন, $\small \frac{AD}{AB}=\frac{AB}{AC}$ থেকে পাই-

$\small AD\cdot AC=\left ( AB \right )^{2}$

সুতরাং, আমরা দেখলাম AC ও AD বহু দ্বারা গঠিত আয়তক্ষেত্রের ক্ষেত্রফল বৃত্তটির ব্যাসের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলের সমান।

অতএব, যে-কোনো সরলরেখার জন্য AC এবং AD দ্বারা গঠিত আয়তক্ষেত্রের ক্ষেত্রফল সর্বদা সমান। ……(ii) (প্রমাণিত)

Support Me

জ্যামিতি : সদৃশ্যতা : কষে দেখি – 18.4

Q7. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)

(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) :

(i) ΔABC ও ΔDEF এ ${\color{Blue} \frac{AB}{DE}=\frac{BC}{FD}=\frac{AC}{EF}}$ হলে,

(a) ∠B = ∠E

(b) ∠A = ∠D

(d) ∠A = ∠F

উত্তর : (c) ∠B = ∠D

সমাধানঃ

ΔABC ও ΔDEF -এ $\small \frac{AB}{DE}=\frac{BC}{FD}=\frac{AC}{EF}$

∴ AB বাহুর বিপরীত কোণ = DE বাহুর বিপরীত কোণ
অর্থ্যাৎ, ∠C = ∠F

একইভাবে,
BC বাহুর বিপরীত কোণ = FD বাহুর বিপরীত কোণ
অর্থ্যাৎ, ∠A = ∠E

AC বাহুর বিপরীত কোণ = EF বাহুর বিপরীত কোণ
অর্থ্যাৎ, ∠B = ∠D

সুতরাং,সঠিক উত্তরটি হবে (c) ∠B = ∠D

জ্যামিতি : সদৃশ্যতা : কষে দেখি – 18.4

Q7. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)

(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) :

(ii) ΔDEF ও ΔPQR এ ∠D = ∠Q এবং ∠R = ∠E হলে, নীচের কোনটি সঠিক নয় লিখি।

(a) $\small {\color{Blue} \frac{EF}{PR}=\frac{DF}{PQ}}$

(b) $\small {\color{Blue} \frac{QR}{PQ}=\frac{EF}{DF}}$

(d) $\small {\color{Blue} \frac{EF}{RP}=\frac{DE}{QR}}$

উত্তর : (a) $\small {\color{Blue} \frac{EF}{PR}=\frac{DF}{PQ}}$

সমাধানঃ

$\because$ ΔDEF ও ΔPQR এ ∠D = ∠Q এবং ∠R = ∠E

অর্থ্যাৎ, $\small \frac{EF}{PR}=\frac{DF}{PQ}$

সুতরাং,সঠিক উত্তরটি হবে (a) $\small {\color{Blue} \frac{EF}{PR}=\frac{DF}{PQ}}$

জ্যামিতি : সদৃশ্যতা : কষে দেখি – 18.4

Q7. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)

(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) :

(iii) ABC ও DEF ত্রিভুজের ∠A = ∠E = 40° , AB : ED = AC : EF এবং ∠F = 65° হলে, ∠B -এর মান

(a) 35°

(b) 65°

(d) 85°

উত্তর : (c) 75°

সমাধানঃ

$\small \because$ ΔABC ও ΔDEF -এ $\small \frac{AB}{ED}=\frac{AC}{EF}$

∴ AB বাহুর বিপরীত কোণ = ED বাহুর বিপরীত কোণ
অর্থ্যাৎ, ∠C = ∠F = 65° [ $\small {\color{Blue} \because }$ ∠F = 65°]

একইভাবে,
AC বাহুর বিপরীত কোণ = EF বাহুর বিপরীত কোণ
অর্থ্যাৎ, ∠B = ∠D

যেহেতু, ত্রিভুজের তিনটি কোণের যোগফল = 180°
∴ ΔABC -এর ∠A + ∠B + ∠C = 180°

মান বসিয়ে পাই –

বা, 40° + ∠B + 65° = 180°

বা, ∠B + 105° = 180°

বা, ∠B = 180° − 105°

∴ ∠B = 75°

জ্যামিতি : সদৃশ্যতা : কষে দেখি – 18.4

Q7. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)

(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) :

(iv) ΔABC এবং ΔPQR এ $\small {\color{Blue} \frac{AB}{QR}=\frac{BC}{PR}=\frac{CA}{PQ}}$ হলে,

(a) ∠A = ∠Q

(b) ∠A = ∠P

(d) ∠B = ∠Q

উত্তর : (a) ∠A = ∠Q

সমাধানঃ

ΔABC ও ΔPQR -এ $\small \frac{AB}{QR}=\frac{BC}{PR}=\frac{CA}{PQ}$

∴ AB বাহুর বিপরীত কোণ = QR বাহুর বিপরীত কোণ
অর্থ্যাৎ, ∠C = ∠P

একইভাবে,
BC বাহুর বিপরীত কোণ = PR বাহুর বিপরীত কোণ
অর্থ্যাৎ, ∠A = ∠Q

CA বাহুর বিপরীত কোণ = PQ বাহুর বিপরীত কোণ
অর্থ্যাৎ, ∠B = ∠R

সুতরাং,সঠিক উত্তরটি হবে (a) ∠A = ∠Q

জ্যামিতি : সদৃশ্যতা : কষে দেখি – 18.4

Q7. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)

(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) :

(v) ABC ত্রিভুজের AB = 9 সেমি., BC = 6 সেমি. এবং CA = 7.5 সেমি.। DEF ত্রিভুজের BC বাহুর অনুরূপ বাহু EF; EF = 8 সেমি. এবং ΔDEF ∼ ΔABC হলে, ΔDEF -এর পরিসীমা

(a) 22.5 সেমি.

(b) 25 সেমি.

(d) 30 সেমি.

উত্তর : (d) 30 সেমি.

সমাধানঃ

$\small \because$ ΔDEF ∼ ΔABC এবং EF ও BC বাহু দুটি হলো অনুরূপ বাহু।

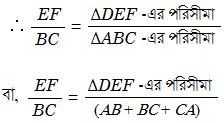
এখন, ত্রিভুজের বাহুগুলির মান বসিয়ে পাই –

বা, ΔDEF -এর পরিসীমা $\small =\frac{4}{3}\times 22.5\; cm.$

∴ ΔDEF -এর পরিসীমা = 30 cm.

জ্যামিতি : সদৃশ্যতা : কষে দেখি – 18.4

Q7. (B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি :

(i) দুটি চতুর্ভুজের অনুরূপ কোণগুলি সমান হলে চতুর্ভুজ দুটি সদৃশ।

সমাধানঃ

বিবৃতিটি মিথ্য।

ব্যাখ্যা :

দুটি চতুর্ভুজের অনুরূপ কোনগুলি সমান হলেও চতুর্ভুজ দুটি সদৃশ্য নাও হতে পারে, কারণ চতুর্ভুজের অনুরূপ কোনগুলির বিপরীত বাহু সর্বদা সমানুপাতী হয় না।

জ্যামিতি : সদৃশ্যতা : কষে দেখি – 18.4

Q7. (B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি :

(ii) পাশের চিত্রে ∠ADE = ∠ACB হলে, ΔADE ∼ ΔACB সদৃশ্যতা

সমাধানঃ

বিবৃতিটি সত্য।

ব্যাখ্যা :

$\small \because$ ΔADE ও ΔACB -এর

∠ADE = ∠ACB (দেওয়া আছে)

∠DAE = ∠BAC (একই কোণ)

এবং অবশিষ্ট ∠AED = অবশিষ্ট ∠ABC

∴ ΔADE ∼ ΔACB

জ্যামিতি : সদৃশ্যতা : কষে দেখি – 18.4

Q7. (B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি :

(iii) ΔPQR -এর QR বাহুর উপর D এমন একটি বিন্দু যে PD ⊥ QR; সুতরাং, ΔPQD ∼ ΔRPD.

সমাধানঃ

বিবৃতিটি মিথ্যা।

ব্যাখ্যা :

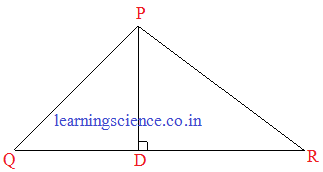
ত্রিভুজের সদৃশ্যতা সংক্রান্ত উপপাদ্য থেকে আমরা জানি যে, “কোনো সমকোণী ত্রিভুজের সমকৌণিক বিন্দু থেকে সমকোনের বিপরীত বাহুর (অর্থাৎ, অতিভুজ) উপর লম্ব টানা হলে যে দুটি ত্রিভুজ উৎপন্ন হয় তারা পরস্পর সদৃশ হয়।”

কিন্তু, এক্ষেত্রে ΔPQR যে সমকোণী ত্রিভুজ যার ∠P = 90° তার কোনো উল্লেখ পাওয়া যায় না – তাই বিবৃতি মিথ্যা।

Koshe dekhi 18.4 class 10

জ্যামিতি : সদৃশ্যতা : কষে দেখি – 18.4

Q7. (C) শূন্যস্থান পূরণ করি :

(i) দুটি ত্রিভুজ সদৃশ হবে যদি তাদের __________বাহুগুলি সমানুপাতী হয়।

সমাধানঃ

দুটি ত্রিভুজ সদৃশ হবে যদি তাদের অনুরূপ বাহুগুলি সমানুপাতী হয়।

জ্যামিতি : সদৃশ্যতা : কষে দেখি – 18.4

Q7. (C) শূন্যস্থান পূরণ করি :

(ii) ΔABC ও ΔDEF -এর পরিসীমা যথাক্রমে 30 সেমি. এবং 18 সেমি.। ΔABC ~ ΔDEF; BC ও EF অনুরূপ বাহু। যদি BC = 9 সেমি. হয়, তাহলে EF = _________ সেমি.।

উত্তরঃ

ΔABC ও ΔDEF -এর পরিসীমা যথাক্রমে 30 সেমি. এবং 18 সেমি.। ΔABC ~ ΔDEF; BC ও EF অনুরূপ বাহু। যদি BC = 9 সেমি. হয়, তাহলে EF = 5.4 সেমি.।

সমাধানঃ

সদৃশ্যতা

জ্যামিতি : সদৃশ্যতা : কষে দেখি – 18.4

Q8. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)

(i) পাশের চিত্রে, ∠ACB = ∠BAD এবং AD ⊥ BC; AC = 15 সেমি., AB = 20 সেমি. এবং BC = 25 সেমি. হলে, AD -এর দৈর্ঘ্য কত তা লিখি।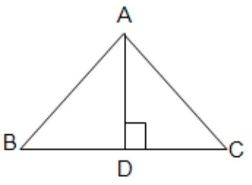 সদৃশ্যতা

উত্তরঃ

AD -এর দৈর্ঘ্য 12 সেমি.

সমাধানঃ

সদৃশ্যতা

জ্যামিতি : সদৃশ্যতা : কষে দেখি – 18.4

Q8. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)

(ii) পাশের চিত্রে, ∠ABC = 90° এবং BD ⊥ AC; যদি AB = 30 সেমি., BD = 24 সেমি. এবং AD = 18 সেমি. হলে, BC -এর দৈর্ঘ্য কত তা লিখি।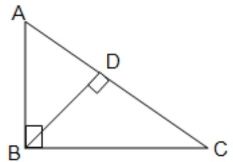 সদৃশ্যতা

উত্তরঃ

BC -এর দৈর্ঘ্য 40 সেমি.

সমাধানঃ

সদৃশ্যতা

যেহেতু, সমকোণী ΔABC -এর সমকৌণিক বিন্দু B থেকে অতিভুজ AC বাহুর উপর BD লম্ব।

অতএব, ΔABD ∼ ΔBDC যাদের

∠BAD = ∠DBC ; ∠ADB = ∠BDC এবং ∠ABD = ∠BCD

এখন, $\small \frac{AB}{BC}=\frac{AD}{BD}$ থেকে পাই-

$\small \frac{30\; cm.}{BC}=\frac{18\; cm.}{24\; cm.}$ [মান বসিয়ে পাই]

বা, $\small \frac{30\; cm.}{BC}=\frac{3}{4}$
বা, $\small 3BC=\left ( 30\times 4 \right )\; cm.$

বা, $\small BC=\frac{30\times 4}{3}\; cm.$

$\small \therefore BC=40\; cm.$ (উত্তর)

জ্যামিতি : সদৃশ্যতা : কষে দেখি – 18.4

Q8. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)

(iii) পাশের চিত্রে, ∠ABC = 90° এবং BD ⊥ AC; যদি BD = 8 সেমি. এবং AD = 4 সেমি. হয়, তাহলে CD -এর দৈর্ঘ্য কত তা লিখি। সদৃশ্যতা

উত্তরঃ

CD -এর দৈর্ঘ্য 16 সেমি.

সমাধানঃ

সদৃশ্যতা

যেহেতু, সমকোণী ΔABC -এর সমকৌণিক বিন্দু B থেকে অতিভুজ AC বাহুর উপর BD লম্ব।

অতএব, ΔABD ∼ ΔBDC যাদের

∠BAD = ∠DBC ; ∠ADB = ∠BDC এবং ∠ABD = ∠BCD

এখন, $\small \frac{BD}{CD}=\frac{AD}{BD}$ থেকে পাই-

$\small \frac{8\; cm.}{CD}=\frac{4\; cm.}{8\; cm.}$ [মান বসিয়ে পাই]

বা, $\small \frac{8\; cm.}{CD}=\frac{1}{2}$
বা, $\small CD=\left ( 8\times 2 \right )\; cm.$

$\small \therefore CD=16\; cm.$ (উত্তর)

জ্যামিতি : সদৃশ্যতা : কষে দেখি – 18.4

Q8. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)

(iv) ABCD ট্রাপিজিয়ামের BC || AD এবং AD = 4 সেমি.। AC ও BD কর্ণদ্বয় এমনভাবে O বিন্দুতে ছেদ করে যে $\small {\color{Blue} \frac{AO}{OC}=\frac{DO}{OB}=\frac{1}{2}}$ হয়। BC -এর দৈর্ঘ্য কত তা লিখি।

উত্তরঃ

BC -এর দৈর্ঘ্য 8 সেমি.

সমাধানঃ

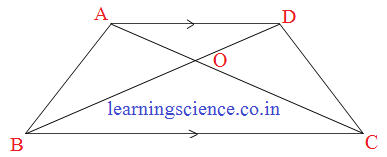
সদৃশ্যতা

$\small \because$ ΔAOD ও ΔBOC -এর

$\small \frac{AO}{OC}=\frac{DO}{OB}$ এবং

∠AOD = বিপ্রতীপ ∠BOC

∴ ΔAOD ∼ ΔBOC

সুতরাং, $\small \frac{AO}{OC}=\frac{DO}{OB}=\frac{AD}{BC}$ [সদৃশ্যকোণী ত্রিভুজের অনুরূপ কোনগুলির বিপরীত বাহুগুলি সমানুপাতী হয়]

এখন, $\small \because \frac{AO}{OC}=\frac{DO}{OB}=\frac{1}{2}$ (দেওয়া আছে)

$\small \therefore \frac{AD}{BC}=\frac{1}{2}$

বা, $\small \frac{4\; cm.}{BC}=\frac{1}{2}\; \; {\color{Blue} \left [ \because AD=4\; cm. \right ]}$

বা, $\small BC=\left ( 4\times 2 \right )\; cm.$

$\small \therefore BC=8\; cm.$ (উত্তর)

জ্যামিতি : সদৃশ্যতা : কষে দেখি – 18.4

Q8. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)

(v) ΔABC ~ ΔDEF এবং ΔABC ও ΔDEF -এ AB, BC ও CA বাহুর অনুরূপ বাহুগুলি যথাক্রমে DE, EF ও DF; ∠A = 47° এবং ∠E = 83° হলে, ∠C -এর পরিমাপ কত তা লিখি।

উত্তরঃ

∠C = 50°

সমাধানঃ

যেহেতু, ΔABC ∼ ΔDEF এবং ΔABC ও ΔDEF -এ AB, BC, ও CA বাহুগুলির অনুরূপ বাহুগুলি হলো যথাক্রমে DE, EF, ও DF

$\small \therefore \frac{AB}{DE}=\frac{BC}{EF}=\frac{CA}{DF}$

সুতরাং, AB বাহুর বিপরীত কোণ = DE বাহুর বিপরীত কোণ

অর্থ্যাৎ, ∠C = ∠F

BC বাহুর বিপরীত কোণ = EF বাহুর বিপরীত কোণ

অর্থ্যাৎ, ∠A = ∠D = 47° ( $\small {\color{Blue} \because }$ ∠A = 47°)

CA বাহুর বিপরীত কোণ = DF বাহুর বিপরীত কোণ

অর্থ্যাৎ, ∠B = ∠E = 83° ( $\small {\color{Blue} \because }$ ∠E = 83°)

আবার, আমরা জানি যে, ত্রিভুজের তিনটি কোণের যোগফল 180° -এর সমান।

∴ ΔABC -এর

∠A + ∠B + ∠C = 180°

এখন, মান বসিয়ে পাই –

বা, 47° + 83° + ∠C = 180°

বা, 130° + ∠C = 180°

বা, ∠C = 180° − 130°

∠C = 50° (উত্তর)

Koshe dekhi 18.4 class 10

Support Me

If you like my work then you can Support me by contributing a small amount which will help me a lot to grow my Website. It’s a request to all of you. You can donate me through phone pay / Paytm/ Gpay on this number 7980608289 or by the link below :

and visit Our website : learningscience.co.in

গণিত প্রকাশ (দশম শ্রেণী) সম্পূর্ণ সমাধান

গণিত প্রকাশ (নবম শ্রেণী) সম্পূর্ণ সমাধান

গণিত প্রভা (ষষ্ঠ শ্রেণী) সম্পূর্ণ সমাধান

জীবন বিজ্ঞান (দশম শ্রেণী) (Life Science)

Thank You

Koshe dekhi 18.4 class 10,Koshe dekhi 18.4 class 10,Koshe dekhi 18.4 class 10,Koshe dekhi 18.4 class 10,Koshe dekhi 18.4 class 10,Koshe dekhi 18.4 class 10,Koshe dekhi 18.4 class 10,Koshe dekhi 18.4 class 10,Koshe dekhi 18.4 class 10,Koshe dekhi 18.4 class 10,Koshe dekhi 18.4 class 10,Koshe dekhi 18.4 class 10,Koshe dekhi 18.4 class 10,Koshe dekhi 18.4 class 10,Koshe dekhi 18.4 class 10,Koshe dekhi 18.4 class 10,Koshe dekhi 18.4 class 10,Koshe dekhi 18.4 class 10

Koshe dekhi 18.4 class 10

Koshe dekhi 18.4 class 10

Koshe dekhi 18.4 class 10

Support Me

Support Me

Koshe dekhi 18.4 class 10

Support Me

Related Post

WBCHSE – Let us Work Out 26.4 – WB Class 10

WBCHSE – Let us Work Out 26.1 – WB Class 10

Koshe Dekhi 21 Class 10

2 thoughts on “Koshe dekhi 18.4 class 10”

Leave a Reply Cancel reply

You missed

Notification Out: RRB NTPC Recruitment 2024

CITL-001 Solved Assignment 2024-25

CIT-003 Solved Assignment 2024-25

CIT-002 Solved Assignment 2024-25