Koshe Dekhi 22 Class 10
Koshe Dekhi 22 Class 10
| Q1. যদি কোনো ত্রিভুজের বাহু তিনটির দৈর্ঘ্য নিম্নরূপ হয়, তবে কোন ক্ষেত্রে ত্রিভুজটি সমকোণী ত্রিভুজ হবে হিসাব করে লিখি : (i) 8 সেমি., 15 সেমি. ও 17 সেমি. (ii) 9 সেমি., 11 সেমি. ও 6 সেমি.
|
| Q2. আমাদের পাড়ার রাস্তায় একটি 15 মিটার লম্বা। মই এমনভাবে রাখা আছে যে মইটি ভূমি থেকে 9 মিটার উঁচুতে অবস্থিত মিলিদের জানালা স্পর্শ করেছে। এবার ওই রাস্তার একই বিন্দুতে মইটির পাদদেশ রেখে মইটিকে ঘুরিয়ে এমভাবে রাখা হলো যে মইটি রাস্তার অপর প্রান্তে অবস্থিত আমাদের জানালা স্পর্শ করল। আমাদের জানালা যদি ভূমি থেকে 12 মিটার উপরে থাকে, তবে পাড়ার ওই রাস্তাটি কত চওড়া হিসাব করে লিখি।
|
| Q3. 10 সেমি. বাহুবিশিষ্ট কোনো রম্বসের একটি কর্ণের দৈর্ঘ্য 12 সেমি. হলে, রম্বসটির অপর কর্ণের দৈর্ঘ্য হিসাব করে লিখি।
|
| Q4. একটি ত্রিভুজ PQR অঙ্কন করেছি যার ∠Q সমকোণ। QR বাহুর উপর S যে-কোনো একটি বিন্দু হলে, প্রমাণ করি যে, PS2 + QR2 = PR2 +QS2
|
| Q5. প্রমাণ করি, যে-কোনো রম্বসের বাহুগুলির উপর অঙ্কিত বর্গের সমষ্টি কর্ণ দুটির উপর অঙ্কিত বর্গ দুটির সমষ্টির সমান হবে।
|
| Q6. ABC একটি সমবাহু ত্রিভুজ। AD, BC বাহুর উপর লম্ব হলে, প্রমাণ করি যে, AB2 + BC2 + CA2 = 4AD2
|
| Q7. একটি সমকোণী ত্রিভুজ ABC অঙ্কন করলাম যার ∠A সমকোণ। AB ও AC বাহুর উপর দুটি বিন্দু যথাক্রমে P ও Q নিলাম। P, Q; B, Q ও C, P যুক্ত করে, প্রমাণ করি যে, BQ2 + PC2 = BC2 + PQ2
|
| Q8. ABCD চতুর্ভুজের দুটি কর্ণ পরস্পরকে লম্বভাবে ছেদ করলে, প্রমাণ করি যে, AB2 + CD2 = BC2 +DA2
|
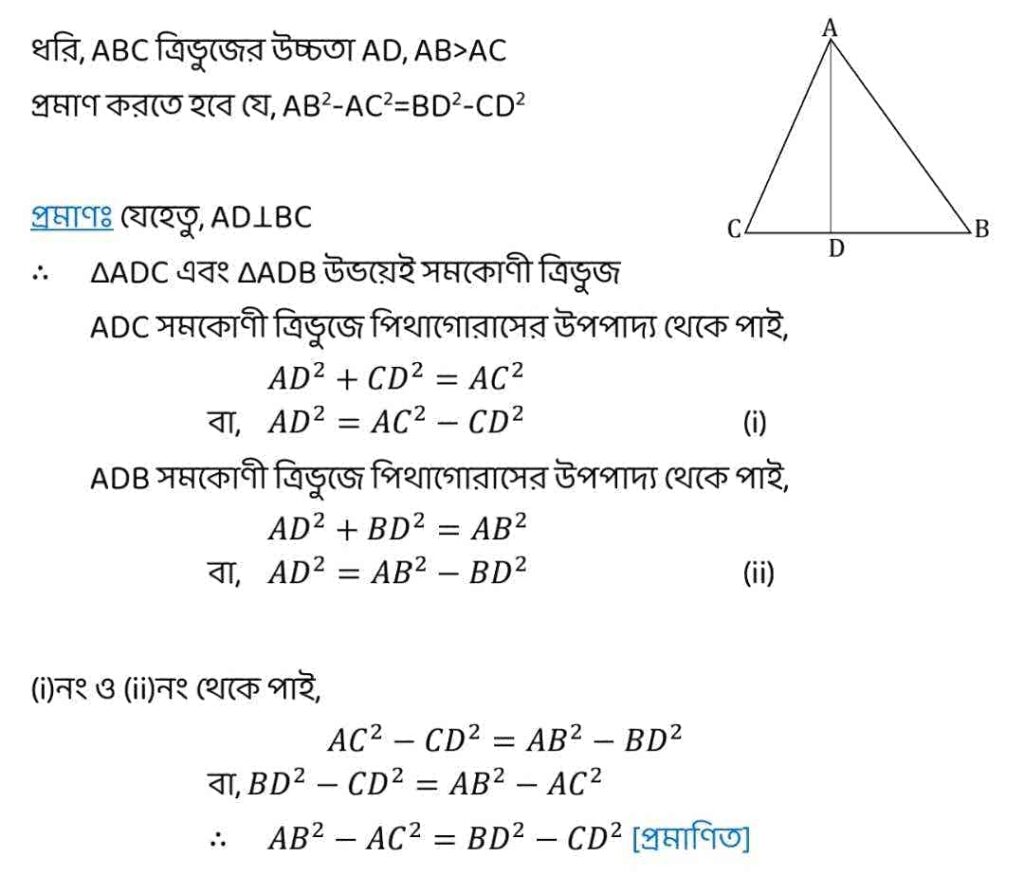
| Q9. একটি ত্রিভুজ ABC অঙ্কন করেছি যার উচ্চতা AD; AB>AC হলে প্রমাণ করি যে, AB2 − AC2 = BD2 − CD2
|
| Q10. ΔABC -এর শীর্ষবিন্দু B ও C থেকে AC ও AB (AC>AB) বাহুদুটির উপর দুটি লম্ব অঙ্কন করেছি যারা পরস্পরকে P বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, AC2 + BP2 = AB2 + CP2
|
| Q11. ABC একটি সমদ্বিবাহু ত্রিভুজ যার ∠C সমকোণ। D, AB-এর উপর যে-কোনো একটি বিন্দু হলে, প্রমাণ করি যে, AD2 + DB2 = 2CD2
|
| Q12. ABC ত্রিভুজের ∠A সমকোণ। CD মধ্যমা হলে, প্রমাণ করি যে, BC2 = CD2 + 3AD2
|
| Q13. ABC ত্রিভুজের অভ্যন্তরস্থ একটি বিন্দু O থেকে BC, CA ও AB বাহুর উপর যথাক্রমে OX, OY ও OZ লম্ব অঙ্কন করেছি। প্রমাণ করি যে, AZ2 + BX2 + CY2 = AY2 + CX2 + BZ2
|
| Q14. RST ত্রিভুজের ∠S সমকোণ। RS ও ST বাহুদ্বয়ের মধ্যবিন্দু যথাক্রমে X ও Y; প্রমাণ করি যে, RY2 + XT2 = 5XY2
|
| Q15. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.) (A) বহুবিকল্পীয় প্রশ্ন (M. C. Q.) : (i) এক ব্যক্তি একটি স্থান থেকে 24 মিটার পশ্চিমদিকে যান এবং তারপর 10 মিটার উত্তর দিকে যান। যাত্রাস্থান থেকে ব্যক্তির দূরত্ব (a) 34 মিটার (b) 17 মিটার (c) 26 মিটার (d) 25 মিটার সমাধানঃ
|
| (ii) ABC একটি সমবাহু ত্রিভুজ এবং AD ⊥ BC হলে, AD2 = (a) (b) 2DC2 (c) 3DC2 (d) 4DC2 সমাধানঃ
|
| (iii) ABC সমদ্বিবাহু ত্রিভুজে AC = BC এবং AB2 = 2AC2 হলে, ∠C -এর পরিমাপ (a) 30° (b) 90° (c) 45° (d) 60° সমাধানঃ
|
| (iv) 13 মিটার ও 7 মিটার উচ্চ দুটি দণ্ড ভূমিতলে লম্বভাবে অবস্থিত এবং তাদের পাদদেশের মধ্যে দূরত্ব 8 মিটার। তাদের শীর্ষদেশের মধ্যে দূরত্ব (a) 9 মিটার (b) 10 মিটার (c) 11 মিটার (d) 12 মিটার সমাধানঃ
|
| (v) একটি রম্বসের দুটি কর্ণের দৈর্ঘ্য 24 সেমি. এবং 10 সেমি. হলে, রম্বসটির পরিসীমা (a) 13 সেমি. (b) 26 সেমি. (c) 52 সেমি. (d) 25 সেমি. সমাধানঃ
|
| (B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি : (i) একটি ত্রিভুজের তিনটি বাহুর দৈর্ঘ্যের অনুপাত 3 : 4 : 5 হলে, ত্রিভুজটি সর্বদা সমকোণী ত্রিভুজ হবে। সমাধানঃ
|
| (ii) 10 সেমি. দৈর্ঘ্যের ব্যাসার্ধবিশিষ্ট একটি বৃত্তে কোনো জ্যা কেন্দ্রে সমকোণ উৎপন্ন করলে জ্যাটির দৈর্ঘ্য 5 সেমি. হবে। সমাধানঃ
|
| (C) শূন্যস্থান পূরণ করি : (i) একটি সমকোণী ত্রিভুজের অতিভুজের উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফল অপর দুটি বাহুর উপর অঙ্কিত বর্গক্ষেত্রের ক্ষেত্রফলের _________ সমান। সমাধানঃ সমষ্টির (ii) একটি সমকোণী সমদ্বিবাহু ত্রিভুজের সমান বাহুদ্বয়ের প্রত্যেকটির দৈর্ঘ্য 42 সেমি. হলে, অতিভুজের দৈর্ঘ্য __________ সেমি.। সমাধানঃ 8 সেমি
(iii) ABCD আয়তাকার চিত্রের AC ও BD কর্ণদ্বয় পরস্পর O বিন্দুতে ছেদ করে। AB = 12 সেমি., AO = 6.5 সেমি. হলে, BC-এর দৈর্ঘ্য __________ সেমি.। সমাধানঃ 5 সেমি
|
| Q16. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) (i) ABC ত্রিভুজের AB = (2a − 1) সেমি., AC = 2√2a সেমি. এবং BC = (2a + 1) সেমি. হলে, ∠BAC -এর মান লিখি। সমাধানঃ
|
(ii) পাশের চিত্রে PQR ত্রিভুজের অভ্যন্তরে O বিন্দু এমনভাবে অবস্থিত যে , ∠PQR = 90°, OP = 6 সেমি. এবং OR = 8 সেমি.। যদি PR = 24 সেমি. এবং ∠QPR = 90° হয়, তাহলে QR বাহুর দৈর্ঘ্য কত তা লিখি।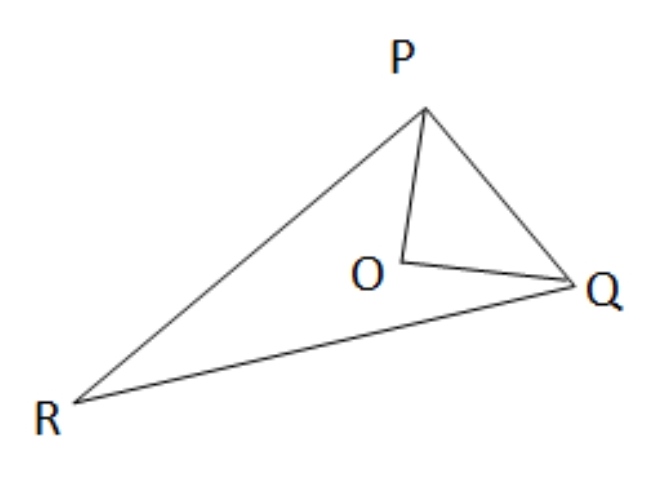 সমাধানঃ
|
| (iii) ABCD আয়তাকার চিত্রের অভ্যন্তরে O বিন্দু এমনভাবে অবস্থিত যে OB = 6 সেমি., OD = 8 সেমি, এবং OA = 5 সেমি.। OC-এর দৈর্ঘ্য নির্ণয় করি। সমাধানঃ
|
| (iv) ABC ত্রিভুজের A বিন্দু থেকে BC বাহুর উপর AD লম্ব BC বাহুর সঙ্গে D বিন্দুতে মিলিত হয়। যদি BD = 8 সেমি., DC = 2 সেমি. এবং AD = 4 সেমি. হয়, তাহলে ∠BAC -এর পরিমাপ কত তা লিখি। সমাধানঃ
|
| (v) ABC সমকোণী ত্রিভুজের ∠ABC = 90°, AB = 3 সেমি., BC = 4 সেমি. এবং B বিন্দু থেকে AC বাহুর উপর লম্ব BD যা AC বাহুর সঙ্গে D বিন্দুতে মিলিত হয়। BD-এর দৈর্ঘ্য নির্ণয় করি। সমাধানঃ
এখন, উত্তরঃ 2.4 সেমি |
koshe dekhi 22 class 10
Koshe Dekhi 22 Class 10,Koshe Dekhi 22 Class 10,Koshe Dekhi 22 Class 10,Koshe Dekhi 22 Class 10,Koshe Dekhi 22 Class 10,Koshe Dekhi 22 Class 10,Koshe Dekhi 22 Class 10,Koshe Dekhi 22 Class 10,Koshe Dekhi 22 Class 10,Koshe Dekhi 22 Class 10,Koshe Dekhi 22 Class 10,Koshe Dekhi 22 Class 10,Koshe Dekhi 22 Class 10,Koshe Dekhi 22 Class 10