Koshe Dekhi 23.3 Class 10 |
koshe dekhi 23.3 class 10
Q1. (i) সমাধানঃ প্রদত্ত, এখন যেহেতু, ধরি, লম্ব = 4k এবং অতিভুজ = 5k পিথাগোরাসের সমীকরণ অনুযায়ী, (লম্ব)² + (ভূমি)² = (অতিভুজ)² বা, (4k)² + (ভূমি)² = (5k)² বা, 16k² + (ভূমি)² = 25k² বা, (ভূমি)² = 25k² − 16k² বা, (ভূমি)² = 9k² বা, ভূমি = এখন যেহেতু, আবার যেহেতু, এখন, হলে,
-এর মান নির্ণয় করে লিখি।
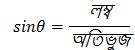
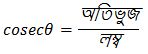
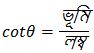
[cosecθ ও cotθ এর মান বসিয়ে পাই]
(উত্তর)
Q1. (ii) যদি সমাধানঃ প্রদত্ত, এখন যেহেতু, ধরি, লম্ব = 3k এবং ভূমি = 4k পিথাগোরাসের সমীকরণ অনুযায়ী, (লম্ব)² + (ভূমি)² = (অতিভুজ)² বা, (3k)² + (4k)² = (অতিভুজ)² বা, 9k² + 16k² = (অতিভুজ)² বা, (অতিভুজ)² = 25k² বা, অতিভুজ = আমরা জানি, এখন, আবার, বামপক্ষ : = ডানপক্ষ ∴ বামপক্ষ = ডানপক্ষ (প্রমানিত) হয়, তবে দেখাই যে,

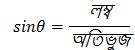
Q1. (iii) tanθ = 1 হলে, সমাধানঃ প্রদত্ত, tanθ = 1 বা, tanθ = tan45° [ ∴ θ = 45° এখন, sinθ = sin45° এবং cosθ = cos45° নির্ণেয় = 2 (উত্তর) -এর মান নির্ণয় করি।
tan45° = 1]
-এর মান
koshe dekhi 23.3 class 10
Q2. (i) cosecθ এবং tanθ কে sinθ -এর মাধ্যমে প্রকাশ করি। সমাধানঃ cosecθ কে sinθ -এর মাধ্যমে প্রকাশ : cosecθ এবং tanθ কে sinθ -এর মাধ্যমে প্রকাশ : tanθ (উত্তর) (উত্তর)
Q2. (ii) cosecθ এবং tanθ কে cosθ -এর মাধ্যমে লিখি। সমাধানঃ cosecθ কে cosθ -এর মাধ্যমে প্রকাশ : cosecθ এবং tanθ কে cosθ -এর মাধ্যমে প্রকাশ : tanθ
Q3. (i) secθ + tanθ = 2 হলে, (secθ − tanθ) -এর মান নির্ণয় করি। সমাধানঃ আমরা জানি, বা, (secθ + tanθ) (secθ − tanθ) = 1 বা, 2 × (secθ − tanθ) = 1 [secθ + tanθ = 2 বসিয়ে পাই] (উত্তর)
Q3. (ii) সমাধানঃ আমরা জানি, বা, (cosecθ + cotθ) (cosecθ − cotθ) = 1 বা, [ বা, বা, [ করণী নিরসন করে পাই ] বা, হলে, cosecθ + cotθ -এর মান হিসাব করে লিখি।
বসিয়ে পাই ]
(উত্তর)
Q3. (iii) sinθ + cosθ = 1 হলে, sinθ × cosθ -এর মান নির্ণয় করি। সমাধানঃ আমরা জানি, বা, বা, [ sinθ + cosθ = 1 বসিয়ে পাই ] বা, বা, (উত্তর)
Q3. (iv) tanθ + cotθ = 2 হলে, (tanθ − cotθ) -এর মান লিখি। সমাধানঃ প্রদত্ত, tanθ + cotθ = 2 বা, বা, বা, বা, বা, (tanθ − 1) = 0 বা, tanθ = 1 বা, tanθ = tan45° ∴ θ = 45° ∴ (tanθ − cotθ) -এর মান = tan45° − cot45° = 1 − 1 = 0 (উত্তর)
Q3. (v) সমাধানঃ আমরা জানি, বা, বা, বা, বা, বা, বা, আবার, বা, বা, বা, বা, বা, হলে, (sinθ + cosθ) -এর মান নির্ণয় করি।
(উত্তর)
Q3. (vi) সমাধানঃ আমরা জানি, বা, বা, বা, বা, হলে, (sinθ + cosθ) -এর মান হিসাব করে লিখি।
(উত্তর)
Q3. (vii) সমাধানঃ আমরা জানি, বা, (secθ + tanθ) (secθ − tanθ) = 1 বা, [ (i) নং সমীকরণ ও (ii) নং সমীকরণ যোগ করে পাই, বা, বা, আবার, (i) নং সমীকরণ থেকে (ii) নং সমীকরণ বিয়োগ করে পাই, বা, বা, হলে, secθ এবং tanθ উভয়ের মান নির্ণয় করি।
……(i)
বসিয়ে পাই]
……(ii)
(উত্তর)
(উত্তর)
Q3. (viii) সমাধানঃ আমরা জানি, বা, (cosecθ + cotθ) (cosecθ − cotθ) = 1 বা, [ (i) নং সমীকরণ ও (ii) নং সমীকরণ যোগ করে পাই, বা, বা, আবার, (i) নং সমীকরণ থেকে (ii) নং সমীকরণ বিয়োগ করে পাই, বা, বা, হলে, cosecθ এবং cotθ – এর মান নির্ণয় করি।
…….(i)
বসিয়ে পাই]
……(ii)
(উত্তর)
(উত্তর)
koshe dekhi 23.3 class 10
Q3. (ix) সমাধানঃ বা, 7sinθ − 7cosθ = sinθ + cosθ বা, 7sinθ − sinθ = cosθ + 7cosθ বা, 6sinθ = 8cosθ বা, হলে, tanθ -এর মান হিসাব করে লিখি।
(উত্তর)
koshe dekhi 23.3 class 10
Q3. (x) সমাধানঃ বা, 5cosecθ − 5sinθ = 3cosecθ + 3sinθ বা, 5cosecθ − 3cosecθ = 5sinθ + 3sinθ বা, 2cosecθ = 8sinθ বা, বা, বা, বা, [ θ সূক্ষকোণের জন্য sinθ ধনাত্মক ] হলে, sinθ -এর মান হিসাব করে লিখি।
(উত্তর)
koshe dekhi 23.3 class 10
Q3. (xi) সমাধানঃ বা, বা, বা, বা, বা, বা, 2cosθ (cosθ − 2) − 1 (cosθ − 2) = 0 বা, (cosθ − 2) (2cosθ − 1) = 0 দুই বা ততোধিক রাশির গুনফল শূন্য হলে তারা পৃথক পৃথক ভাবে শূন্য হয়। অর্থাৎ, (cosθ − 2) = 0 বা, cosθ = 2 আবার, (2cosθ − 1) = 0 বা, 2cosθ = 1 ∴ ∴ (secθ − cosθ) -এর মান আবার, ∴ (secθ − cosθ) -এর মান হলে, (secθ − cosθ) -এর মান হিসাব করে লিখি।
[যখন cosθ = 2]
[যখন
]
(উত্তর)
koshe dekhi 23.3 class 10
Q3. (xii) সমাধানঃ বা, বা, বা, বা, বা, বা, বা, বা, বা, ∴ tanθ = ±1 (উত্তর) সম্পর্কটি থেকে tanθ -এর মান নির্ণয় করি।
koshe dekhi 23.3 class 10
Q3. (xiii) সমাধানঃ বা, বা, বা, বা, বা, বা, বা, বা, বা, বা, বা, বা, ধরি, θ সূক্ষকোণ তাই ধনাত্মক মান নিয়ে পাই, (i) + (ii) করে পাই, হলে, (tanθ + cotθ) এবং (tanθ − cotθ) এর মান নির্ণয় করি এবং সেখান থেকে tanθ -এর মান হিসাব করে লিখি।
(উত্তর)
(উত্তর)
……..(i)
……..(ii)
(উত্তর)
koshe dekhi 23.3 class 10
Q3. (xiv) সমাধানঃ হলে,
-এর মান হিসাব করে লিখি।
(উত্তর)
koshe dekhi 23.3 class 10
Q4. (i) PQR ত্রিভজে ∠Q সমকোণ। সমাধানঃ যেহেতু, এবং P কোণের সাপেক্ষে, ভূমি = PQ ও অতিভুজ = PR একইভাবে, R কোণের সাপেক্ষে, ভূমি = RQ এবং অতিভুজ = PR ∴ (cosP − cosR) এর মান একক এবং PQ − RQ = 1 একক হলে, (cosP − cosR) এর মান নির্ণয় করি।


(উত্তর)
koshe dekhi 23.3 class 10
Q4. (ii) XYZ ত্রিভূজে সমাধানঃ যেহেতু, এবং X কোণের সাপেক্ষে, ভূমি = XY ও অতিভুজ = XZ একইভাবে, এবং X কোণের সাপেক্ষে, লম্ব = YZ ও ভূমি = XY ∴ secX − tanX এর মান সমকোণ।
একক এবং XZ − YZ = 2 একক হলে, secX − tanX এর মান নির্ণয় করি।

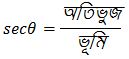

(উত্তর)
Q5. সম্পর্কগুলি থেকে θ কে অপনয়ন করি : (i) x = 2 sinθ , y = 3 cosθ সমাধানঃ x = 2 sinθ বা, বা, বা, আবার, y = 3 cosθ বা, বা, বা, (i) ও (ii) নং সমীকরণ দুটিকে যোগ করে পাই, …….(i)
…….(ii)
(উত্তর)
Q5. সম্পর্কগুলি থেকে θ কে অপনয়ন করি : (ii) সমাধানঃ বা, বা, বা, আবার, বা, বা, বা, (i) নং সমীকরণ থেকে (ii) নং সমীকরণ বিয়োগ করে পাই, বা, …….(i)
…….(ii)
(উত্তর)
Q6. (i) যদি সমাধানঃ প্রদত্ত, যেহেতু, ∴ ধরি, লম্ব = 5k এবং অতিভুজ = 13k পিথাগোরাসের সমীকরণ অনুযায়ী, (লম্ব)² + (ভূমি)² = (অতিভুজ)² বা, (5k)² + (ভূমি)² = (13k)² বা, 25k² + (ভূমি)² = 169k² বা, (ভূমি)² = 169k² − 25k² বা, (ভূমি)² = 144k² বা, ভূমি = আবার, এবং এখন, tanα + secα = 1.5 (প্রমানিত) হয়, তাহলে দেখাই যে,
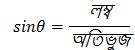

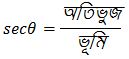
Q6. (ii) যদি সমাধানঃ প্রদত্ত, আমরা জানি, ∴ ধরি, লম্ব = nk এবং ভূমি = mk পিথাগোরাসের সমীকরণ অনুযায়ী, (লম্ব)² + (ভূমি)² = (অতিভুজ)² বা, (nk)² + (mk)² = (অতিভুজ)² বা, n²k² + m²k² = (অতিভুজ)² বা, (অতিভুজ)² = k²(n² + m²) বা, অতিভুজ = আবার, আমরা জানি, ∴ sinA এর মান এবং ∴ secA এর মান হয়, তাহলে sinA এবং secA উভয়ের মান লিখি।

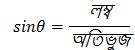
(উত্তর)
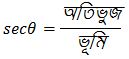
(উত্তর)
Q6. (iii) যদি সমাধানঃ প্রদত্ত, ধরি, ভূমি = xk এবং অতিভুজ পিথাগোরাসের সমীকরণ অনুযায়ী, (লম্ব)² + (ভূমি)² = (অতিভুজ)² বা, (লম্ব)² + (xk)² বা, (লম্ব)² + x²k² = k²(x² + y²) বা, (লম্ব)² = k²(x² + y²) − x²k² বা, (লম্ব)² = x²k²+ k²y² − x²k² বা, (লম্ব)² = k²y² বা, লম্ব = ∴ লম্ব = yk আমরা জানি, বামপক্ষ : x sinθ ডানপক্ষ : y cosθ বামপক্ষ = ডানপক্ষ (প্রমানিত) হয়, তাহলে দেখাই যে, xsinθ = ycosθ

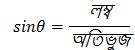
Q6. (iv) যদি সমাধানঃ প্রদত্ত, যেহেতু, ∴ ধরি, লম্ব = (a² − b²)k এবং অতিভুজ = (a² + b²)k পিথাগোরাসের সমীকরণ অনুযায়ী, (লম্ব)² + (ভূমি)² = (অতিভুজ)² বা, {(a² − b²)k}² + (ভূমি)² = {(a² + b²)k}² বা, (a² − b²)²k² + (ভূমি)² = (a² + b²)²k² বা, (ভূমি)² = (a² + b²)²k² − (a² − b²)²k² বা, (ভূমি)² = k²{(a² + b²)² −(a² − b²)²} বা, (ভূমি)² = k²(4a²b²) [∵ (a + b)² −(a − b)² = 4ab] বা, ভূমি = ∴ ভূমি = 2abk আবার আমরা জানি, ∴ cotα হয়, তাহলে দেখাই যে,
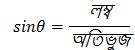
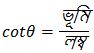
(প্রমানিত)
koshe dekhi 23.3 class 10
Q6. (v) যদি সমাধানঃ ধরি, ∴ sinθ = xk, cosθ = yk আমরা জানি, বা, বা, বা, বা, বা, বামপক্ষ : sinθ − cosθ = xk − yk = k (x − y) = ডানপক্ষ (প্রমানিত) হয়, তাহলে দেখাই যে,
koshe dekhi 23.3 class 10
Q6. (vi) যদি সমাধানঃ প্রদত্ত, বা, আমরা জানি, ∴ ধরি, ভূমি = 4xk এবং অতিভুজ = k(1 + 4x²) পিথাগোরাসের সমীকরণ অনুযায়ী, (লম্ব)² + (ভূমি)² = (অতিভুজ)² বা, (লম্ব)² + (4xk)² = {k(1 + 4x²)}² বা, (লম্ব)² + 16x²k² = k²(1 + 4x²)² বা, (লম্ব)² = k²(1 + 4x²)² − 16x²k² বা, (লম্ব)² = k²{(1 + 4x²)² − 16x²} বা, (লম্ব)² = k²{(1 + 4x²)² − 4.1.4x²} বা, (লম্ব)² = k²(1 − 4x²)² বা, লম্ব = ∴ লম্ব আবার আমরা জানি, এবং বামপক্ষ : cosecA + cotA = ডানপক্ষ (প্রমানিত) হয়, তাহলে দেখাই যে,

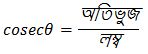
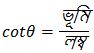
koshe dekhi 23.3 class 10
Q7. যদি x = a sinθ এবং y = b tanθ হয়, তাহলে প্রমান করি, সমাধানঃ x = a sinθ বা, বা, বা, আবার, y = b tanθ বা, বা, বা, (i) নং সমীকরণ থেকে (ii) নং সমীকরণ বিয়োগ করে পাই, বা, …….(i)
…….(ii)
(প্রমানিত)
koshe dekhi 23.3 class 10
Q৪. যদি সমাধানঃ প্রদত্ত, sinθ + sin²θ = 1 বা, sinθ = 1 − sin²θ বা, sinθ = cos²θ এখন, বামপক্ষ : = sinθ + sin²θ = 1 = ডানপক্ষ (প্রমানিত) হয়, তাহলে প্রমান করি যে,
Q9. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.) : (A) বহুবিকল্পনীয় প্রশ্ন (M.C.Q.) : (i) যদি 3x = cosec α এবং (a) (b) (c) (d) সমাধানঃ আমরা জানি, cosec²α − cot²α = 1 cosecα ও cotα এর মান বসিয়ে পাই, বা, বা, বা, উত্তরঃ (c) হয়, তাহলে
-এর মান
Q9.(A) (ii) যদি 2x = sec A এবং (a) (b) (c) (d) সমাধানঃ আমরা জানি, sec²A − tan²A = 1 secA ও tanA এর মান বসিয়ে পাই, বা, বা, বা, উত্তরঃ (a) হয়, তাহলে
-এর মান
Q9.(A) (iii) tan α + cot α = 2 হলে, (a) 1 (b) 0 (c) 2 (d) কোনোটিই নয় সমাধানঃ প্রদত্ত, tanα + cotα = 2 বা, বা, বা, বা, বা, বা, tanα − 1 = 0 ∴ tanα = 1 = 1 + 1 = 2 উত্তরঃ (c) এর মান
koshe dekhi 23.3 class 10
Q9.(A) (iv) যদি (a) 1 (b) 2 (c) (d) সমাধানঃ প্রদত্ত, sinθ − cosθ = 0 বা, sinθ = cosθ বা, ∴ cosecθ = secθ আবার আমরা জানি, sin²θ + cos²θ = 1 বা, sin²θ + sin²θ = 1 [যেহেতু, sinθ = cosθ] বা, 2sin²θ = 1 বা, বা, বা, sinθ = sin45° ∴ θ = 45° প্রদত্ত, secθ + cosecθ = x বা, sec45° + cosec45° = x বা, উত্তরঃ (d) এবং secθ + cosecθ = x হয়, তাহলে x এর মান
koshe dekhi 23.3 class 10
Q9.(A) (v) 2 cos 3θ = 1 হলে, θ এর মান (a) 10° (b) 15° (c) 20° (d) 30° সমাধানঃ প্রদত্ত, 2 cos3θ = 1 cos3θ = cos60° 3θ = 60° ∴ θ = 20° উত্তরঃ (c)
koshe dekhi 23.3 class 10
(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি : (i) যদি সমাধানঃ আমরা জানি, a sec²θ + b cos²θ এর সর্বনিম্ন মান নির্ণেয়, sec²α + cos²α রাশিমালার সর্বনিম্ন মানের ক্ষেত্রে a = 1 এবং b = 1 ∴ sec²α + cos²α রাশিমালার সর্বনিম্ন মান = 2 অর্থাৎ, প্রদত্ত উক্তিটি সত্য। হয়, তাহলে
-এর সর্বনিম্ন মান 2
যেখানে a এবং b যথাক্রমে sec²θ ও cos²θ এর সহগ।
koshe dekhi 23.3 class 10
(B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি : (ii) সমাধানঃ = 0 অর্থাৎ, প্রদত্ত উক্তিটি মিথ্যা। এর মান 1
[ ∵ cos90° = 0]
koshe dekhi 23.3 class 10
(C) শূন্যস্থান পূরণ করি : (i) সমাধানঃ = 4 × 1 = 4 (উত্তর) – এর মান _________ ।
koshe dekhi 23.3 class 10
(C) শূন্যস্থান পূরণ করি : (ii) সমাধানঃ বা, sin (θ − 30°) = sin 30° বা, (θ − 30°) = 30° বা, θ = 30°+ 30° ∴ θ = 60° ∴ cosθ -এর মান = cos60° হলে, cosθ -এর মান _________ ।
(উত্তর)
koshe dekhi 23.3 class 10
(C) শূন্যস্থান পূরণ করি : (iii) সমাধানঃ হলে,
এর মান _________ ।
(উত্তর)
koshe dekhi 23.3 class 10
Q10. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) : (i) যদি সমাধানঃ উভয়পক্ষে বর্গ করে পাই, বা, আবার, r sinθ = 2 উভয়পক্ষে বর্গ করে পাই, বা, (i) ও (ii) যোগ করে পাই, বা, বা, r2 × 1 = 16 বা, r2 = 16 ∴ r = 4 (উত্তর) প্রদত্ত, rsinθ = 2 বা, 4 × sinθ = 2 বা, বা, বা, sinθ = sin 30° ∴ θ = 30° (উত্তর) এবং 0° < θ < 90° হয়, তাহলে r ও θ এর মান নির্ণয় করি।
…… (i)
.. …. (ii)
koshe dekhi 23.3 class 10
Q10. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) : (ii) যদি sin A + sin B = 2 হয়, যেখানে 0°≤ A ≤ 90° এবং 0°≤ B ≤ 90° তাহলে (cos A + cos B) এর মান নির্ণয় করি। সমাধানঃ যেহেতু, আমরা জানি, sinθ এর সর্বোচ্চ মান 1 , যেখানে θ = 90° ∴ sinA + sinB = 2 সম্ভব হবে যদি sinA = sinB = 1 হয়। অর্থাৎ, A = B = 90º সুতরাং, cosA = cosB = cos90º = 0 নির্ণেয় (cos A + cos B) এর মান = 0 + 0 = 0 (উত্তর)
koshe dekhi 23.3 class 10
Q10. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) : (iii) যদি 0°< θ < 90° হয়, তাহলে সমাধানঃ আমরা জানি, a tan²θ + b cot²θ এর সর্বনিম্ন মান নির্ণেয়, 9 tan²θ +4 cot²θ রাশিমালার সর্বনিম্ন মানের ক্ষেত্রে a = 9 এবং b = 4 ∴ 9 tan²θ +4 cot²θ রাশিমালার সর্বনিম্ন মান = 2 × 3 × 2 = 12 (উত্তর) -এর সর্বনিন্ম মান নির্ণয় করি।
যেখানে a এবং b যথাক্রমে tan²θ ও cot²θ এর সহগ।
koshe dekhi 23.3 class 10
Q10. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) : (iv) সমাধানঃ = 1 (উত্তর) -এর মান নির্ণয় করি।
koshe dekhi 23.3 class 10
Q10. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) : (v) যদি cosec2 θ = 2 cot θ এবং 0°< θ < 90° হয়, তাহলে θ এর মান নির্ণয় করি। সমাধানঃ cosec2 θ = 2 cot θ বা, 1 + cot2 θ = 2 cot θ বা, cot2 θ − 2 cot θ + 1 = 0 বা, (cot θ − 1)2 = 0 বা, cot θ − 1 = 0 বা, cot θ = 1 বা, cot θ = cot 45° ∴ θ = 45° (উত্তর)
koshe dekhi 23.3 class 10
koshe dekhi 23.3 class 10
kose dekhi 23.3 class 10
