Koshe Dekhi 25 Class 10

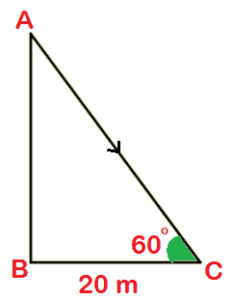
Q1. একটি নারকেল গাছের গোড়া থেকে অনুভূমিক তলে 20 মিটার দূরের একটি বিন্দুর সাপেক্ষে গাছটির অগ্রভাগের উন্নতি কোণ যদি 60° হয়, তাহলে গাছটির উচ্চতা নির্ণয় করি।

সমাধানঃ

koshe dekhi 25_height and distance

ধরি AB হলো নারকেল গাছের উচ্চতা (নির্ণয় করতে হবে)।

B হল নারকেল গাছের গোড়া এবং A হল নারকেল গাছের অগ্রভাগ।

B বিন্দু থেকে অনুভূমিক তলে 20 মিটার (= BC) দূরে অবস্থিত C বিন্দুর সাপেক্ষে গাছটির অগ্রভাগ অর্থাৎ A বিন্দুর উন্নতি কোণ ∠ACB = 60°

এখন সমকোণী ΔABC থেকে ∠ACB -এর সাপেক্ষে

tan ∠ACB = লম্ব / ভূমি

বা, $tan60^{\circ}=\frac{AB}{BC}$ [যেহেতু, ∠ACB = 60°]

বা, $\sqrt{3}=\frac{AB}{20}$ [যেহেতু, tan 60° = √3]

∴ $AB=20\sqrt{3}$ মিটার

উত্তরঃ নির্ণেয় নারকেল গাছটির উচ্চতা 20√3 মিটার।

Koshe Dekhi 25 Class 10

Q2. সূর্যের উন্নতি কোণ যখন 30° তখন একটি স্তম্ভের ছায়ার দৈর্ঘ্য 9 মিটার হয়। স্তম্ভটির উচ্চতা হিসাব করে লিখি।

সমাধানঃ

koshe dekhi 25_height and distance

ধরি, AB = স্তম্ভের উচ্চতা (যা নির্ণয় করতে হবে)

BC = 9 মিটার = স্তম্ভের ছায়ার দৈর্ঘ্য যখন সূর্যের উন্নতি কোণ 30° অর্থাৎ, ∠ACB = 30°

এখন, সমকোণী ত্রিভুজ ABC থেকে ∠ACB -এর সাপেক্ষে পাই –

tan ∠ACB = লম্ব / ভূমি

বা, $tan30^{\circ}=\frac{AB}{BC}$ [যেহেতু, ∠ACB = 30°]

বা, $\frac{1}{\sqrt{3}}=\frac{AB}{9}$ [যেহেতু, ${\color{Blue} tan30^{\circ}=\frac{1}{\sqrt{3}}}$ ]

বা, $AB=\frac{9}{\sqrt{3}}=\frac{9\sqrt{3}}{\sqrt{3}\times \sqrt{3}}=3\sqrt{3}$

∴ $AB=3\sqrt{3}$ মিটার

উত্তরঃ নির্ণেয় স্তম্ভটির উচ্চতা 3√3 মিটার।

Koshe Dekhi 25 Class 10

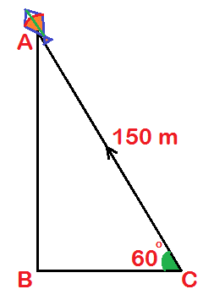
Q3. 150 মি. লম্বা সুতো দিয়ে একটি মাঠ থেকে ঘুড়ি ওড়ানো হয়েছে। ঘুড়িটি যদি অনুভূমিক রেখার সঙ্গে 60° কোণ করে উড়তে থাকে, তাহলে ঘুড়িটি মাঠ থেকে কত উঁচুতে রয়েছে হিসাব করে লিখি।

সমাধানঃ

koshe dekhi 25_height and distance

ধরি, মাঠের উপর অবস্থিত C বিন্দু থেকে একটি ঘুড়ি ওড়ানো হচ্ছে। ঘুড়িটি যখন A বিন্দুতে উড়ছে তখন সুতোর দৈর্ঘ্য (অর্থাৎ, AC) 150 মিটার।

C বিন্দুর সাপেক্ষে ঘুড়িটি মাঠের সাপেক্ষে ∠ACB = 60° কোণ করে উড়ছে।

এক্ষেত্রে, ঘুড়িটি মাটি বা মাঠ থেকে AB উচ্চতায় উড়ছে (যার দৈর্ঘ্য আমাদের নির্ণয় করতে হবে)।

এখন, সমকোণী ত্রিভুজ ABC থেকে ∠ACB -এর সাপেক্ষে পাই –

sin ∠ACB = লম্ব / অতিভুজ

বা, $sin60^{\circ}=\frac{AB}{AC}$ [যেহেতু, ∠ACB = 60°]

বা, $\frac{\sqrt{3}}{2}=\frac{AB}{150}$ [যেহেতু, ${\color{Blue} sin60^{\circ}=\frac{\sqrt{3}}{2}}$ ]

∴ AB = 75 √3 মিটার

উত্তরঃ নির্ণেয় ঘুড়িটি মাঠ থেকে 75 √3 মিটার উঁচুতে ছিল।

Koshe Dekhi 25 Class 10

Q4. একটি নদীর একটি পাড়ের একটি তালগাছের সোজাসুজি অপর পাড়ে একটি খুটি পুতলাম। এবার নদীর পাড় ধরে ওই খুটি থেকে ${\color{Blue} 7\sqrt{3}}$ মিটার সরে গিয়ে দেখছি নদীর পাড়ের পরিপ্রেক্ষিতে গাছটির পাদদেশ 60° কোণে রয়েছে। নদীটি কত মিটার চওড়া নির্ণয় করি।

সমাধানঃ

koshe dekhi 25_height and distance

ধরা যাক, AB = নদীটির প্রস্থ (নির্ণয় করতে হবে)।

নদীর ওপারের A বিন্দুতে তাল গাছটি অবস্থিত এবং নদীর এপারের B বিন্দুতে খুঁটিটি পোঁতা আছে। B বিন্দু থেকে নদীর পাড় ধরে 7√3 মিটার দূরের একটি বিন্দু C থেকে নদীর অপর পাড়ের সঙ্গে তাল গাছের পাদবিন্দু (অর্থাৎ A বিন্দু) ∠ACB = 60° কোণ উৎপন্ন হয়েছে।

এখন সমকোণী ΔABC থেকে ∠ACB -এর সাপেক্ষে পাই –

tan ∠ACB = লম্ব / ভূমি

বা, $tan60^{\circ}=\frac{AB}{BC}$ [যেহেতু, ∠ACB = 60°]

বা, $\sqrt{3}=\frac{AB}{7\sqrt{3}}$ [যেহেতু, tan 60° = √3]

বা, $AB=7\sqrt{3}\times \sqrt{3}=7\times 3$

∴ AB = 21 মিটার

উত্তরঃ নির্ণেয় নদীটি 21 মিটার চওড়া।

Koshe Dekhi 25 Class 10

Q5. ঝড়ে একটি টেলিগ্রাফপোস্টে মাটি থেকে কিছু উপরে মচকে যাওয়ায় তার অগ্রভাগ গোড়া থেকে ${\color{Blue} 8\sqrt{3}}$ মিটার দুরে মাটি স্পর্শ করেছে এবং অনুভূমিক রেখার সঙ্গে 30° কোণ উৎপন্ন করেছে। পোস্টটি মাটি থেকে কত উপরে মচকে ছিল এবং পোস্টটির উচ্চতা কত ছিল হিসাব করে লিখি।

সমাধানঃ

koshe dekhi 25_height and distance

ধরি, BX = টেলিগ্রাফ পোস্টের উচ্চতা (নির্ণয় করতে হবে)।

ঝড়ে পোস্টটির অগ্রভাগ (অর্থাৎ, X বিন্দুটি) A বিন্দু থেকে মচকে গিয়ে অনুভূমিক তলের উপর অবস্থিত C বিন্দুতে মাটিকে স্পর্শ করেছে এবং অনুভূমিকের সঙ্গে ∠ACB = 30° কোণ উৎপন্ন করেছে।

এক্ষেত্রে, AX = AC এবং BC = 8√3 মিটার।

যেহেতু, পোস্টটি A বিন্দু থেকে মচকে যায়।
∴ BA = পোস্টটির গোড়া থেকে মচকে যাওয়ার অবস্থান পর্যন্ত উচ্চতা/দূরত্ব (নির্ণয় করতে হবে)।

এখন, সমকোণী ত্রিভুজ ABC থেকে ∠ACB -এর সাপেক্ষে পাই –

tan ∠ACB = লম্ব / ভূমি

বা, $tan30^{\circ}=\frac{AB}{BC}$ [যেহেতু, ∠ACB = 30°]

বা, $\frac{1}{\sqrt{3}}=\frac{AB}{8\sqrt{3}}$ [যেহেতু, ${\color{Blue} tan30^{\circ}=\frac{1}{\sqrt{3}}}$ ]

∴ AB = 8 মিটার

সুতরাং, পোস্টটি মাটি থেকে 8 মিটার উপর থেকে মচকে গেছিলো। (উত্তর)

আবার, সমকোণী ত্রিভুজ ABC থেকে ∠ACB -এর সাপেক্ষে পাই –

sin ∠ACB = লম্ব / অতিভুজ

বা, $sin30^{\circ}=\frac{AB}{AC}$ [যেহেতু, ∠ACB = 30°]

বা, $\frac{1}{2}=\frac{8}{AC}$ [যেহেতু, ${\color{Blue} sin30^{\circ}=\frac{1}{2}}$ ]

∴ AC = 16 মিটার।

এখন, BX = AB + AX

বা, BX = AB + AC [যেহেতু, AX = AC]

বা, BX = (8 + 16) মিটার

∴ BX = 24 মিটার।

সুতরাং, পোস্টটির উচ্চতা 24 মিটার।

উত্তরঃ নির্ণেয় পোস্টটি মাটি থেকে 8 মিটার উঁচুতে মচকে গেছিলো এবং পোস্টটির উচ্চতা 24 মিটার।

Koshe Dekhi 25 Class 10

Q6. আমাদের পাড়ায় রাস্তার দু-পাশে পরস্পর বিপরীত দিকে দুটি বাড়ি আছে। প্রথম বাড়ির দেয়ালের গোড়া থেকে 6 মিটার দূরে একটি মই-এর গোড়া রেখে যদি মইটিকে দেয়ালে ঠেকানো যায়, তবে তা অনুভূমিক রেখার সঙ্গে 30° কোণ উৎপন্ন করে। কিন্তু মইটিকে যদি একই জায়গায় রেখে দ্বিতীয় বাড়ির দেয়ালে লাগানো যায়, তাহলে অনুভূমিক রেখার সঙ্গে 60° কোণ উৎপন্ন করে।

(i) মইটির দৈর্ঘ্য নির্ণয় করি।

(ii) দ্বিতীয় বাড়ির দেয়ালের গোড়া থেকে মইটির গোড়া কত দূরে রয়েছে হিসাব করে লিখি।

(iii) রাস্তাটি কত চওড়া নির্ণয় করি।

(iv) দ্বিতীয় বাড়ির কত উঁচুতে মইটির অগ্রভাগ স্পর্শ করবে নির্ণয় করি।

সমাধানঃ

koshe dekhi 25_height and distance

ধরি, AB = প্রথম বাড়ির উচ্চতা।
CD = দ্বিতীয় বাড়ির উচ্চতা।
MP = NP = মইয়ের দৈর্ঘ্য (নির্ণয় করতে হবে)।

প্রথম বাড়ির গোড়া অর্থাৎ B বিন্দু থেকে 6 মিটার দূরের একটি বিন্দু P তে মইটি রেখে প্রথম বাড়ির দেওয়ালের M বিন্দুতে মইটির অগ্রভাগ স্পর্শ করানো হলো, যার ফলে অনুভূমিক এর সঙ্গে মইটির মধ্যে ∠MPB = 30° কোণ উৎপন্ন করেছে এবং P বিন্দু থেকেই যখন দ্বিতীয় বাড়ির N বিন্দুতে মইটি ঠেকানো হয়, তখন তা অনুভূমিকের সঙ্গে ∠NPC = 60° কোণ উৎপন্ন করে।

BP = প্রথম বাড়ির দেওয়ালের গোড়া থেকে মইয়ের পাদদেশের দূরত্ব = 6 মিটার।
CP = দ্বিতীয় বাড়ির দেওয়ালের গোড়া থেকে মইয়ের পাদদেশের দূরত্ব (নির্ণয় করতে হবে)।
BC = রাস্তাটির প্রস্থ (নির্ণয় করতে হবে)।
CN = দ্বিতীয় বাড়ির দেওয়ালের গোড়া থেকে মইয়ের অগ্রভাগের স্পর্শবিন্দুর উচ্চতা (নির্ণয় করতে হবে)।

সমকোণী ত্রিভুজ MBP থেকে ∠MPB -এর সাপেক্ষে পাই –

cos ∠MPB = ভূমি / অতিভুজ

বা, $cos\, 30^{\circ}=\frac{BP}{MP}$

বা, $\frac{\sqrt{3}}{2}=\frac{6}{MP}$

বা, $MP\times \sqrt{3}=2\times 6$

বা, $MP=\frac{2\times 2\times 3}{\sqrt{3}}$

∴ MP = 4√3

উত্তরঃ (i) মইটির দৈর্ঘ্য 4√3 মিটার।

সমকোণী ত্রিভুজ NCP থেকে ∠NPC -এর সাপেক্ষে পাই –

cos ∠NPC = ভূমি / অতিভুজ

বা, $cos\, 60^{\circ}=\frac{CP}{NP}$

বা, $\frac{1}{2}=\frac{CP}{4\sqrt{3}}$ [যেহেতু, MP = NP = 4√3 মিটার ]

বা, $CP\times 2=4\sqrt{3}$

বা, $CP=\frac{4\sqrt{3}}{2}$

∴ CP = 2√3

উত্তরঃ (ii) দ্বিতীয় বাড়ির দেয়ালের গোড়া থেকে মইটির গোড়া 2√3 মিটার দূরে রয়েছে।

রাস্তাটি চওড়া

= BC

= BP + PC

= (6 + 2√3) মিটার

= 2 (3 + √3) মিটার

উত্তরঃ (iii) রাস্তাটি 2 (3 + √3) মিটার চওড়া।

সমকোণী ত্রিভুজ NCP থেকে ∠NPC -এর সাপেক্ষে পাই –

tan ∠NPC = লম্ব / ভূমি

বা, $tan\, 60^{\circ}=\frac{CN}{CP}$

বা, $\sqrt{3}=\frac{CN}{2\sqrt{3}}$

বা, $CN=2\sqrt{3}\times \sqrt{3}$

∴ CN = 6

উত্তরঃ (iv) দ্বিতীয় বাড়ির 6 মিটার উঁচুতে মইটির অগ্রভাগ স্পর্শ করবে।

Koshe Dekhi 25 Class 10

Q7. যদি একটি চিমনির গোড়ার সঙ্গে সমতলে অবস্থিত একটি বিন্দুর সাপেক্ষে চিমনির চূড়ার উন্নতি কোণ 60° হয় এবং সেই বিন্দু ও চিমনির গোড়ার সঙ্গে একই সরলরেখায় অবস্থিত ওই বিন্দু থেকে আরও 24 মিটার দূরের অপর একটি বিন্দুর সাপেক্ষে চিমনির চুড়ার উন্নতি কোণ 30° হয়, তাহলে চিমনির উচ্চতা হিসাব করে লিখি। [√3 -এর আসন্ন মান 1.732 ধরে তিন দশমিক স্থান পর্যন্ত আসন্ন মান নির্ণয় করি]

সমাধানঃ

koshe dekhi 25_height and distance

ধরি, AB = চিমনির উচ্চতা (নির্ণয় করতে হবে)।

চিমনির গোড়া অর্থাৎ B বিন্দু থেকে একই সমতলে অবস্থিত C বিন্দুর সাপেক্ষে চিমনির চূড়া অর্থাৎ, A বিন্দুর উন্নতি কোণ 60° অর্থাৎ ∠ACB = 60°। আবার, C বিন্দু থেকে একই সমতলে আরো 24 মিটার দূরে অবস্থিত D বিন্দুর সাপেক্ষে A বিন্দুর উন্নতি কোণ 30° অর্থাৎ ∠ADB = 30°
এক্ষেত্রে, DC = 24 মিটার এবং BC = x মিটার (ধরি)।

সমকোণী ত্রিভুজ ABC থেকে ∠ACB -এর সাপেক্ষে পাই –

tan ∠ACB = লম্ব / ভূমি

বা, $tan\, 60^{\circ}=\frac{AB}{BC}$

বা, $\sqrt{3}=\frac{AB}{x}$

বা, $x=\frac{AB}{\sqrt{3}}$ ……(i)

সমকোণী ত্রিভুজ ABD থেকে ∠ADB -এর সাপেক্ষে পাই –

tan ∠ADB = লম্ব / ভূমি

বা, $tan\, 30^{\circ}=\frac{AB}{BD}$

বা, $\frac{1}{\sqrt{3}}=\frac{AB}{BC+CD}$

বা, $\frac{1}{\sqrt{3}}=\frac{AB}{x+24}$

বা, $AB\times \sqrt{3}=x+24$

বা, $\sqrt{3}AB-24=x$ …….(ii)

(i) ও (ii) তুলনা করে পাই,

$\sqrt{3}AB-24=\frac{AB}{\sqrt{3}}$

বা, 3AB − 24√3 = AB

বা, 3AB − AB = 24√3

বা, 2AB = 24√3

বা, AB = 12√3

বা, AB = 12 × 1.732

∴ AB = 20.784

উত্তরঃ চিমনির উচ্চতা 20.784 মিটার।

Koshe Dekhi 25 Class 10

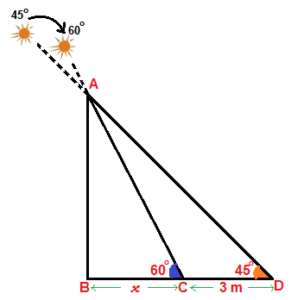
Q8. সূর্যের উন্নতি কোণ 45° থেকে বৃদ্ধি পেয়ে 60° হলে, একটি খুঁটির ছায়ার দৈর্ঘ্য 3 মিটার কমে যায়। খুঁটিটির উচ্চতা নির্ণয় করি। [√3 = 1.732 ধরে তিন দশমিক স্থান পর্যন্ত আসন্ন মান নির্ণয় করি]।

সমাধানঃ

koshe dekhi 25_height and distance

ধরি, AB = খুঁটির উচ্চতা (নির্ণয় করতে হবে)
সূর্যের উন্নতি কোণ যখন 45° অর্থাৎ, ∠ADB = 45° তখন AB খুঁটির ছায়ার দৈর্ঘ্য হয় BD এবং সূর্যের উন্নতি কোণ যখন 60° খুঁটির ছায়ার দৈর্ঘ্য হয় BC ।

ধরি, BC = x মিটার।

এক্ষেত্রে, ছায়ার দৈর্ঘ্য হ্রাস পায় 3 মিটার অর্থাৎ, DC = 3 মিটার।

সমকোণী ত্রিভুজ ABC থেকে ∠ACB -এর সাপেক্ষে পাই –

tan ∠ACB = লম্ব / ভূমি

বা, $tan\, 60^{\circ}=\frac{AB}{BC}$

বা, $\sqrt{3}=\frac{AB}{x}$

বা, $x=\frac{AB}{\sqrt{3}}$ ……(i)

সমকোণী ত্রিভুজ ABD থেকে ∠ADB -এর সাপেক্ষে পাই –

tan ∠ADB = লম্ব / ভূমি

বা, $tan\, 45^{\circ}=\frac{AB}{BD}$

বা, $1=\frac{AB}{BC+CD}$

বা, $1=\frac{AB}{x+3}$

বা, AB = x + 3

বা, AB − 3 = x …….(ii)

(i) ও (ii) তুলনা করে পাই,

$\frac{AB}{\sqrt{3}}=AB-3$

বা, AB = √3AB − 3√3

বা, AB − √3AB = − 3√3

বা, AB (1 − √3) = − 3√3

বা, $AB=\frac{-3\sqrt{3}}{\left ( 1-\sqrt{3} \right )}$

বা, $AB=\frac{-3\sqrt{3}}{-\left ( \sqrt{3}-1 \right )}$

বা, $AB=\frac{3\sqrt{3}}{\left ( \sqrt{3}-1 \right )}$

বা, $AB=\frac{3\times 1.732}{\left ( 1.732-1 \right )}$

বা, $AB=\frac{3\times 1.732}{.732}$

বা, $AB=\frac{3\times 1732}{732}$

∴ AB = 7.098

উত্তরঃ নির্ণেয় খুঁটিটির উচ্চতা 7.098 মিটার ।

Koshe Dekhi 25 Class 10

Q9. ${\color{Blue} 9\sqrt{3}}$ মিটার উঁচু তিনতলা বাড়ির ছাদ থেকে দেখলে 30 মিটার দূরে অবস্থিত একটি কারখানার চিমনির উন্নতি কোণ 30° হয়। চিমনির উচ্চতা হিসাব করে লিখি।

সমাধানঃ

koshe dekhi 25_height and distance

ধরি, ED = BC = তিন তলা বাড়ির উচ্চতা = 9√3 মিটার।
AC = চিমনির উচ্চতা (নির্ণয় করতে হবে)।
CD = বাড়ি থেকে চিমনির দূরত্ব = BE = 30 মিটার।

E বিন্দু থেকে DC এর সমান্তরাল করে BE সরলরেখা অঙ্কন করা হলো যা AC কে B বিন্দুতে ছেদ করে।
তিনতলা বাড়ির ছাদের মধ্যে অবস্থিত E বিন্দুর সাপেক্ষে চিমনির চূড়া অর্থাৎ, A বিন্দুর উন্নতি কোণ 30° অর্থাৎ, ∠AEB = 30°

সমকোণী ত্রিভুজ ABE থেকে ∠AEB -এর সাপেক্ষে পাই –

tan ∠AEB = লম্ব / ভূমি

বা, $tan\, 30^{\circ}=\frac{AB}{BE}$

বা, $\frac{1}{\sqrt{3}}=\frac{AB}{30}$

বা, $AB=\frac{30}{\sqrt{3}}$

∴ AB = 10√3 মিটার

∴ চিমনির উচ্চতা

= AC

= AB + BC

= 10√3 মিটার + 9√3 মিটার

= 19√3 মিটার

উত্তরঃ নির্ণেয় চিমনির উচ্চতা 19√3 মিটার।

Koshe Dekhi 25 Class 10

Q10. একটি লাইট হাউস থেকে তার সঙ্গে একই সরলরেখায় অবস্থিত দুটি জাহাজের মাস্তুলের গোড়ার অবনতি কোণ যদি যথাক্রমে 60° ও 30° হয় এবং কাছের জাহাজের মাস্তুলে যদি লাইট হাউস থেকে 150 মিটার দূরত্বে থাকে, তাহলে দূরের জাহাজের মাস্তুল লাইট হাউস থেকে কত দূরত্বে রয়েছে এবং লাইট হাউসটির উচ্চতা হিসাব করে লিখি।

সমাধানঃ

Koshe dekhi 25 class 10

ধরি, CD = লাইট হাউসের উচ্চতা (নির্ণয় করতে হবে)।
লাইট হাউসের C বিন্দু থেকে লাইট হাউসের সঙ্গে একই সমতলে অবস্থিত দুটি জাহাজের মাস্তুল B এবং A বিন্দুর অবনতি কোণ যথাক্রমে 60° ও 30° অর্থাৎ ∠ECB = 60° এবং ∠ECA = 30°

DB = লাইট হাউসের গোড়া থেকে কাছের জাহাজের মাস্তুলের দূরত্ব = 150 মিটার।
DA = লাইট হাউসের গোড়া থেকে দূরের জাহাজের মাস্তুলের দূরত্ব (নির্ণয় করতে হবে)।

সমকোণী ত্রিভুজ BCD থেকে পাই,

tan ∠CBD = লম্ব / ভূমি

$tan60^{\circ}=\frac{CD}{BD}$

$\sqrt{3}=\frac{CD}{150}$

∴ CD = 150√3

সমকোণী ত্রিভুজ ACD থেকে পাই,

tan ∠CAD = লম্ব / ভূমি

$tan30^{\circ}=\frac{CD}{AD}$

$\frac{1}{\sqrt{3}}=\frac{150\sqrt{3}}{AD}$

AD = 150√3 × √3

∴ CD = 450

উত্তরঃ দূরের জাহাজের মাস্তুল লাইট হাউস থেকে 450 মিটার দূরত্বে রয়েছে এবং লাইট হাউসটির উচ্চতা 150√3 মিটার।

Koshe Dekhi 25 Class 10

Q11. একটি পাচতলা বাড়ির ছাদের কোনো বিন্দু থেকে দেখলে মনুমেন্টের চুড়ার উন্নতি কোণ ও গোড়ার অবনতি কোণ যথাক্রমে 60° ও 30°; বাড়ির উচ্চতা 16 মিটার হলে, মনুমেন্টের উচ্চতা এবং বাড়িটি মনুমেন্ট থেকে কত দূরে অবস্থিত হিসাব করে লিখি।

সমাধানঃ

Koshe dekhi 25 class 10

ধরি, AB একটি পাঁচতোলা বাড়ি, যার ছাদ A বিন্দু থেকে মনুমেন্টের চূড়া C বিন্দুর উন্নতি কোণ এবং গোড়া D বিন্দুর অবনতি কোণ যথাক্রমে 60° এবং 30°

বাড়ির উচ্চতা AB = 16 মিটার

∴ ∠CAE = 60° [ ধরি AE// BD]

∠EAD = 30°

∴ ∠ADB = ∠EAD = 30°

সমকোণী ত্রিভুজ ADB থেকে পাই,

tan 30° = লম্ব / ভূমি

$tan30^{\circ}=\frac{AB}{BD}$

$\frac{1}{\sqrt{3}}=\frac{16}{BD}$

∴ BD = 16√3 = AE

সমকোণী ত্রিভুজ AEC থেকে পাই,

tan 60° = লম্ব / ভূমি

$tan60^{\circ}=\frac{CE}{AE}$

$\sqrt{3}=\frac{CE}{16\sqrt{3}}$

CE = 16√3 × √3

∴ CE = 48

∴ CD

= CE + ED

= CE + AB

= 48 + 16

= 64

উত্তরঃ মনুমেন্টের উচ্চতা 64 মিটার এবং বাড়িটি মনুমেন্ট থেকে 16√3 মিটার দূরে অবস্থিত।

Koshe Dekhi 25 Class 10

Q12. 250 মিটার লম্বা সুতো দিয়ে একটি ঘুড়ি ওড়াচ্ছি। সুতোটি যখন অনুভূমিক রেখার সঙ্গে 60° কোণ করে থাকে এবং সুতোটি যখন অনুভূমিক রেখার সঙ্গে 45° কোণ করে তখন প্রতিক্ষেত্রে ঘুড়িটি আমার থেকে কত উপরে থাকবে হিসাব করে লিখি। এদের মধ্যে কোন ক্ষেত্রে ঘুড়িটি বেশি উঁচুতে থাকবে নির্ণয় করি।

সমাধানঃ

Koshe Dekhi 25 Class 10

Q13. উড়োজাহাজের একজন যাত্রী কোনো এক সময় তার এক পাশে হাওড়া স্টেশনটি এবং ঠিক বিপরীত পাশে। শহিদ মিনারটি যথাক্রমে 60° ও 30° অবনতি কোণে দেখতে পান। ওই সময়ে উড়োজাহাজটি যদি ${\color{Blue} 545\sqrt{3}}$ মিটার উঁচুতে থাকে, তাহলে হাওড়া স্টেশন ও শহিদ মিনারের দূরত্ব নির্ণয় করি।

সমাধানঃ

Koshe Dekhi 25 Class 10

Q14. একটি তিনতলা বাড়ির ছাদে 3.3 মিটার দৈর্ঘ্যের একটি পতাকা আছে। রাস্তার কোনো এক স্থান থেকে দেখলে পতাকা দন্ডটির চুড়া ও পাদদেশের উন্নতি কোণ যথাক্রমে 50° ও 45° হয়। তিনতলা বাড়িটির উচ্চতা হিসাব করে লিখি। [ধরি, tan50° = 1.192]

সমাধানঃ

Koshe Dekhi 25 Class 10

Q15. দুটি স্তম্ভের উচ্চতা যথাক্রমে 180 মিটার ও 60 মিটার। দ্বিতীয় স্তম্ভটির গোড়া থেকে প্রথমটির চুড়ার উন্নতি কোণ 60° হলে, প্রথমটির গোড়া থেকে দ্বিতীয়টির চুড়ার উন্নতি কোণ হিসাব করে লিখি।

সমাধানঃ

Koshe Dekhi 25 Class 10

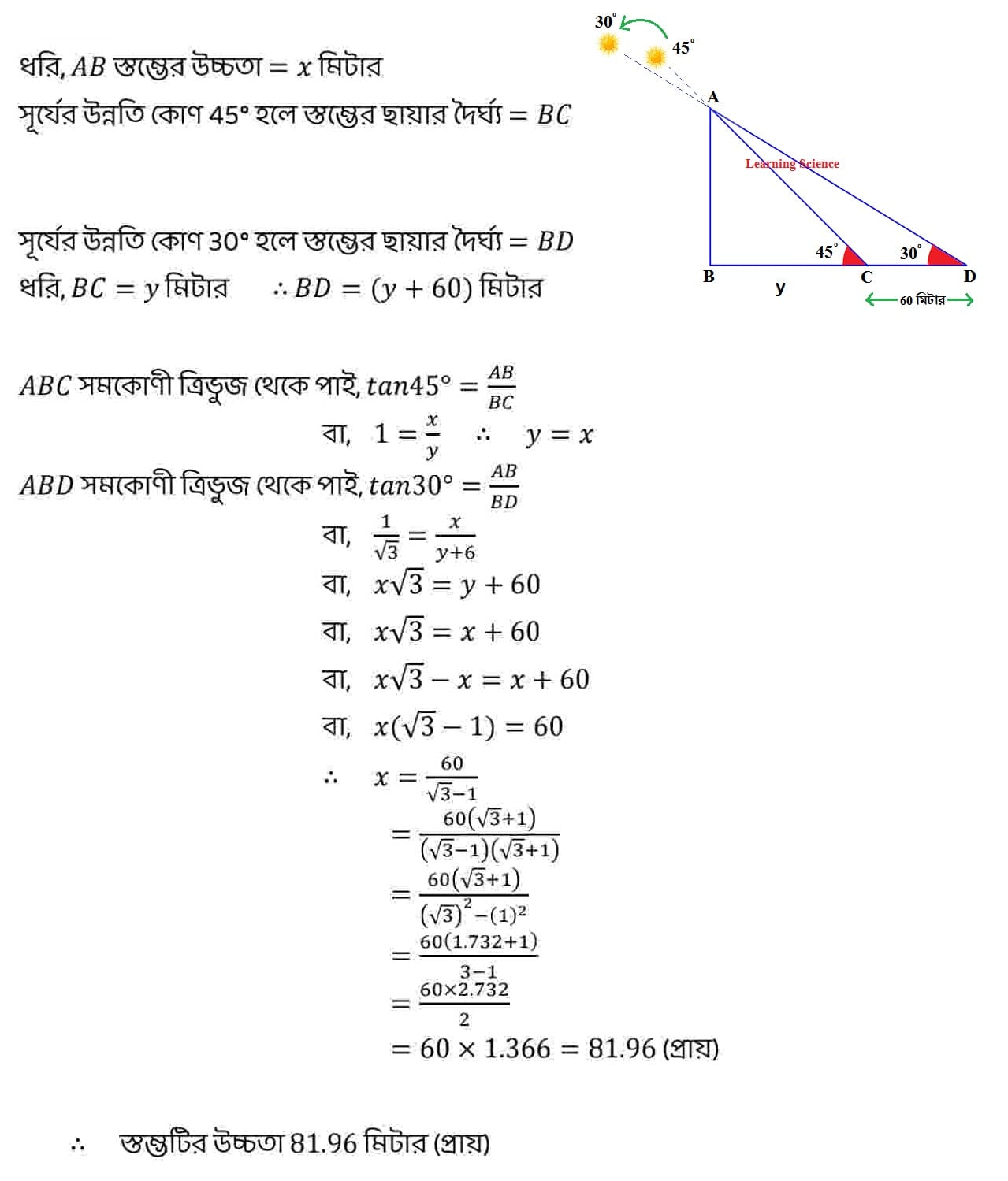
Q16. সূর্যের উন্নতি কোণ 45° হলে, কোনো সমতলে অবস্থিত একটি স্তম্ভের ছায়ার দৈর্ঘ্য যা হয়, উন্নতি কোণ 30° হলে, ছায়ার দৈর্ঘ্য তার চেয়ে 60 মিটার বেশি হয়। স্তম্ভটির উচ্চতা নির্ণয় করি।

সমাধানঃ

Koshe Dekhi 25 Class 10

Q17. একটি চিমনির সঙ্গে একই সমতলে অবস্থিত অনুভূমিক সরলরেখায় কোনো এক বিন্দু থেকে চিমনির দিকে 50 মিটার এগিয়ে যাওয়ায় তার চুড়ার উন্নতি কোণ 30° থেকে 60° হলো। চিমনির উচ্চতা হিসাব করে লিখি।

সমাধানঃ

Koshe Dekhi 25 Class 10

Q18. 126 ডেসিমি উঁচু একটি উলম্ব খুটি মাটি থেকে কিছু উপরে দুমড়ে গিয়ে উপরের অংশ কাত হয়ে পড়ায় তার অগ্রভাগ মাটি স্পর্শ করে ভূমির সঙ্গে 30° কোণ উৎপন্ন করেছে। খুটিটি কত উপরে দুমড়ে গিয়েছিল এবং তার অগ্রভাগ গোড়া থেকে কত দূরে মাটি স্পর্শ করেছিল হিসাব করে লিখি।

সমাধানঃ

Koshe Dekhi 25 Class 10

Q19. মাঠের মাঝখানে দাঁড়িয়ে মোহিত একটি উড়ন্ত পাখিকে প্রথমে উত্তরদিকে 30° উন্নতি কোণে এবং 2 মিনিট পরে দক্ষিণদিকে 60° উন্নতি কোণে দেখতে পেল। পাখিটি যদি একই সরলরেখা বরাবর 50√3 মিটার উঁচুতে উড়ে। থাকে, তবে তার গতিবেগ কিলোমিটার প্রতি ঘন্টায় নির্ণয় করি।

সমাধানঃ

Koshe Dekhi 25 Class 10

Q20. 5√3 মিটার উঁচু একটি রেলওয়ে ওভারব্রিজে দাঁড়িয়ে আমিতাদিদি প্রথমে একটি ট্রেনের ইঞ্জিনকে ব্রিজের এপারে 30° অবনতি কোণে দেখলেন। কিন্তু 2 সেকেন্ড পরই ওই ইঞ্জিনকে ব্রিজের ওপারে 45° অবনতি কোণে দেখলেন। ট্রেনটির গতিবেগ মিটার প্রতি সেকেন্ডে হিসাব করে লিখি।

সমাধানঃ

5√3 মিটার উঁচু একটি রেলওয়ে ওভারব্রিজে দাঁড়িয়ে আমিতাদিদি প্রথমে একটি ট্রেনের ইঞ্জিনকে ব্রিজের এপারে 30° অবনতি কোণে দেখলেন। কিন্তু 2 সেকেন্ড পরই ওই ইঞ্জিনকে ব্রিজের ওপারে 45° অবনতি কোণে দেখলেন। ট্রেনটির গতিবেগ মিটার প্রতি সেকেন্ডে হিসাব করে লিখি।

Koshe Dekhi 25 Class 10

Q21. একটি নদীর পাড়ের সঙ্গে লম্বভাবে একটি সেতু আছে। সেতুটির একটি পাড়ের প্রান্ত থেকে নদীর পাড় ধরে কিছু দূর গেলে সেতুর অপর প্রান্তটি 45° কোণে দেখা যায় এবং পাড় ধরে আরও 400 মিটার দূরে সরে গেলে সেই প্রান্তটি 30° কোণে দেখা যায়। সেতুটির দৈর্ঘ্য নির্ণয় করি।

Koshe Dekhi 25 Class 10

Q22. একটি পার্কের একপ্রান্তে অবস্থিত 15 মিটার উঁচু একটি বাড়ির ছাদ থেকে পার্কের অপর পারে অবস্থিত একটি ইটভাটার চিমনির পাদদেশ ও অগ্রভাগ যথাক্রমে 30° অবনতি কোন ও 60° উন্নতি কোন দেখা যায়। ইটভাটার চিমনির উচ্চতা ও বাড়ির মধ্যে দূরত্ব নির্ণয় করি।

সমাধানঃ

koshe dekhi 25 class 10

Koshe Dekhi 25 Class 10

Q23. একটি উড়োজাহাজ থেকে রাস্তায় পরপর দুটি কিলোমিটার ফলকের অবনতি কোণ যথাক্রমে 60° ও 30° হলে, উড়োজাহাজটির উচ্চতা নির্ণয় করি,

(i) যখন ফলক দুটি উড়োজাহাজের বিপরীত পাশে অবস্থিত,

(ii) যখন ফলক দুটি উড়োজাহাজের একই পাশে অবস্থিত।

সমাধানঃ

(i) Koshe dekhi 25 class 10

ধরি, উড়োজাহাজের C বিন্দুর থেকে B বিন্দুর অবনতি কোণ 60° এবং A বিন্দুর অবনতি কোণ 30° । উড়োজাহাজের C বিন্দু ভূমি থেকে CD উচ্চতায় আছে।

মনেকরি, BD = x মি.

∴ BD = (1000 − x ) মি.

সমকোণী ত্রিভুজ CBD থেকে ∠CBD -এর সাপেক্ষে পাই –

tan ∠CBD = লম্ব / ভূমি

বা, $tan\, 60^{\circ}=\frac{CD}{BD}$

বা, $\sqrt{3}=\frac{CD}{x}$

বা, $CD=x\sqrt{3}......\left ( i \right )$

সমকোণী ত্রিভুজ CAD থেকে ∠CAD -এর সাপেক্ষে পাই –

tan ∠CAD = লম্ব / ভূমি

বা, $tan\, 30^{\circ}=\frac{CD}{AD}$

বা, $\frac{1}{\sqrt{3}}=\frac{CD}{1000-x}$

বা, $CD\sqrt{3}=1000-x$

বা, $CD=\frac{1000-x}{\sqrt{3}}......\left ( ii \right )$

(i) ও (ii)-কে তুলনা করে পাই

$x\sqrt{3}=\frac{1000-x}{\sqrt{3}}$

বা, $3x=1000-x\; \; {\color{Blue} \left [ \because \sqrt{3}\times \sqrt{3}=3 \right ]}$

বা, 3x + x = 1000

বা, 4x = 1000

∴ $x=\frac{1000}{4}=250$ মিটার

(i) নং সমীকরণে x -এর মান বসিয়ে পাই –

CD = 250√3 মিটার.

উত্তরঃ ফলক দুটি উড়োজাহাজের বিপরীত পার্শে হলে, উড়োজাহাজের উচ্চতা = 250√3 মিটার.

(ii) Koshe dekhi 25 class 10

মনেকরি, BD = x মি.

∴ BD = (1000 + x ) মি.

সমকোণী ত্রিভুজ CBD থেকে ∠CBD -এর সাপেক্ষে পাই –

tan ∠CBD = লম্ব / ভূমি

বা, $tan\, 60^{\circ}=\frac{CD}{BD}$

বা, $\sqrt{3}=\frac{CD}{x}$

বা, $CD=x\sqrt{3}......\left ( i \right )$

সমকোণী ত্রিভুজ CAD থেকে ∠CAD -এর সাপেক্ষে পাই –

tan ∠CAD = লম্ব / ভূমি

বা, $tan\, 30^{\circ}=\frac{CD}{AD}$

বা, $\frac{1}{\sqrt{3}}=\frac{CD}{1000+x}$

বা, $CD\sqrt{3}=1000+x$

বা, $CD=\frac{1000+x}{\sqrt{3}}......\left ( ii \right )$

(i) ও (ii)-কে তুলনা করে পাই

$x\sqrt{3}=\frac{1000+x}{\sqrt{3}}$

বা, $3x=1000+x\; \; {\color{Blue} \left [ \because \sqrt{3}\times \sqrt{3}=3 \right ]}$

বা, 3x − x = 1000

বা, 2x = 1000

∴ $x=\frac{1000}{2}=500$ মিটার

(i) নং সমীকরণে x -এর মান বসিয়ে পাই –

CD = 500√3 মিটার.

উত্তরঃ ফলক দুটি উড়োজাহাজের বিপরীত পার্শে হলে, উড়োজাহাজের উচ্চতা = 500√3 মিটার.

উত্তরঃ

Koshe Dekhi 25 Class 10

Q24. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)

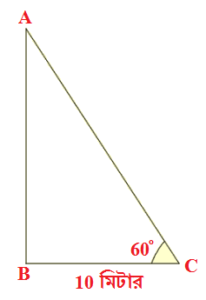
(A) বহুবিকল্পীয় প্রশ্ন: (M.C.Q.) :

(i) মাঠের উপর একটি বিন্দু থেকে মোবাইল টাওয়ারের চূড়ার উন্নতি কোণ 60° এবং টাওয়ারের গোড়া থেকে ওই বিন্দুর দূরত্ব 10 মিটার। টাওয়ারের উচ্চতা

(a) 10 মিটার

(b) 10√3 মিটার

(d) 100 মিটার

উত্তরঃ (b) 10√3 মিটার

সমাধানঃ

koshe dekhi 25_class 10

ধরি, AB হলো মোবাইল টাওয়ারের উচ্চতা এবং BC হলো টাওয়ারের গোড়া থেকে নিদৃষ্ট বিন্দু C -এর দূরত্ব। C বিন্দু থেকে টাওয়ারের চূড়া অর্থাৎ A বিন্দুর উন্নতি কোণ ∠ACB এর মান হলো 60°

এক্ষেত্রে, BC = 10 মিটার

এখন সমকোণী ΔABC থেকে ∠ACB -এর সাপেক্ষে

tan ∠ACB = লম্ব / ভূমি

বা, $tan60^{\circ}=\frac{AB}{BC}$ [যেহেতু, ∠ACB = 60°]

বা, $\sqrt{3}=\frac{AB}{10}$ [যেহেতু, tan 60° = √3]

∴ $AB=10\sqrt{3}$ মিটার [উত্তর : (b)]

Koshe Dekhi 25 Class 10

Q24. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)

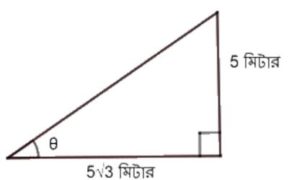
(A) বহুবিকল্পীয় প্রশ্ন: (M.C.Q.) :

(ii) ত্রিকোণমিতিক অনুপাতের প্রয়োগ θ – এর মান –

(a) 30°

(b) 45°

(d) 75°

সমাধানঃ

tan θ = লম্ব / ভূমি

বা, $tan\, \theta =\frac{5}{5\sqrt{3}}$

বা, $tan\, \theta =\frac{1}{\sqrt{3}}$

বা, tan θ = tan 30°

∴ θ = 30°

উত্তরঃ (a) 30°

Koshe Dekhi 25 Class 10

Q24. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)

(A) বহুবিকল্পীয় প্রশ্ন: (M.C.Q.) :

(iii) তিনতলা বাড়ির ছাদ থেকে মাটিতে পড়ে থাকা একটি বাক্সকে যত কোণে দেখলে বাড়ির উচ্চতা ও বাড়ি থেকে বাক্সটির দূরত্ব সমান হয় তা হলো,

(a) 15°

(b) 30°

(d) 60°

সমাধানঃ

ধরি, বাড়ির উচ্চতা = AB ও বাড়ি থেকে বাক্সটির দূরত্ব = BC

প্রশ্নানুসারে,

AB = BC

সমকোণী ত্রিভুজ ABC থেকে ∠ACB -এর সাপেক্ষে পাই –

tan ∠ACB = লম্ব / ভূমি

বা, $tan\, \theta =\frac{AB}{BC}$

বা, $tan\, \theta =\frac{AB}{AB}$

বা, tan θ = 1

বা, tan θ = tan 45°

∴ θ = 45°

উত্তরঃ (c) 45°

Koshe Dekhi 25 Class 10

Q24. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)

(A) বহুবিকল্পীয় প্রশ্ন: (M.C.Q.) :

(iv) একটি টাওয়ারের উচ্চতা ${\color{Blue} 100\sqrt{3}}$ মিটার। টাওয়ারের পাদবিন্দু থেকে 100 মিটার দূরে একটি বিন্দু থেকে টাওয়ারের চূড়ার উন্নতি কোণ –

(a) 30°

(b) 45°

(d) কোনোটিই নয়

সমাধানঃ

koshe dekhi 25 class 10

ধরি, টাওয়ারের উচ্চতা = AB = 100√3 মিটার ও টাওয়ারের পাদবিন্দু থেকে একটি বিন্দুর দূরত্ব = BC = 100 মিটার

সমকোণী ত্রিভুজ ABC থেকে ∠ACB -এর সাপেক্ষে পাই –

tan ∠ACB = লম্ব / ভূমি

বা, $tan\, \theta =\frac{AB}{BC}$

বা, $tan\, \theta =\frac{100\sqrt{3}}{100}$

বা, tan θ = √3

বা, tan θ = tan 60°

∴ θ = 60°

উত্তরঃ (c) 60°

Koshe Dekhi 25 Class 10

Q24. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)

(A) বহুবিকল্পীয় প্রশ্ন: (M.C.Q.) :

(v) একটি পোস্টের ভূমিতলে ছায়ার দৈর্ঘ্য পোস্টের উচ্চতার √3 গুণ হলে, সূর্যের উন্নতি কোণ

(a) 30°

(b) 45°

(d) কোনোটিই নয়।

সমাধানঃ

ধরি, পোস্টের উচ্চতা = AB = x একক ও পোস্টের ভূমিতলে ছায়ার দৈর্ঘ্য = BC = x√3 একক।

ধরি, সূর্যের উন্নতি কোণ = θ

সমকোণী ত্রিভুজ ABC থেকে ∠ACB -এর সাপেক্ষে পাই –

tan ∠ACB = লম্ব / ভূমি

বা, $tan\, \theta =\frac{AB}{BC}$

বা, $tan\, \theta =\frac{x}{x\sqrt{3}}$

বা, $tan\, \theta =\frac{1}{\sqrt{3}}$

বা, tan θ = tan 30°

∴ θ = 30°

উত্তরঃ (a) 30°

Koshe Dekhi 25 Class 10

24 (B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি :

(i) ΔABC -এর ∠B = 90°, AB = BC, হলে, ∠C = 60°.

উত্তরঃ বিবৃতিটি মিথ্যা।

ব্যাখ্যাঃ ΔABC -এর ∠B = 90°, AB = BC হলে, ΔABC হবে সমকোণী সমদ্বিবাহু ত্রিভুজ। সুতরাং, সমকোণী সমদ্বিবাহু ত্রিভুজের সূক্ষকোণ দুটির প্রতিটির মান 45° অর্থাৎ ∠C = 45° হবে।

(ii) ত্রিকোণমিতিক অনুপাতের প্রয়োগ PQ একটি বাড়ির উচ্চতা, QR ভূমি। P বিন্দু থেকে R বিন্দুর অবনতি কোণ ∠SPR; সুতরাং, ∠SPR = ∠PRQ.

উত্তরঃ বিবৃতিটি সত্য।

ব্যাখ্যাঃ যেহেতু PS ।। QR এবং PR ভেদক

∴ ∠SPR = একান্তর ∠PRQ

Koshe Dekhi 25 Class 10

24 (C) শূন্যস্থান পূরণ করি :

(i) সূর্যের উন্নতি কোণ 30° থেকে বৃদ্ধি পেয়ে 60° হলে, একটি পোস্টের ছায়ার দৈর্ঘ্য _____ পায়। (হ্রাস/বৃদ্ধি)

উত্তরঃ সূর্যের উন্নতি কোণ 30° থেকে বৃদ্ধি পেয়ে 60° হলে, একটি পোস্টের ছায়ার দৈর্ঘ্য হ্রাস পায়।

(ii) সূর্যের উন্নতি কোণ 45° হলে, একটি পোস্টের দৈর্ঘ্য ও তার ছায়ার দৈর্ঘ্য _______ হবে।

উত্তরঃ সূর্যের উন্নতি কোণ 45° হলে, একটি পোস্টের দৈর্ঘ্য ও তার ছায়ার দৈর্ঘ্য সমান হবে।

(iii) যখন সূর্যের উন্নতি কোণ 45°-এর _______তখন একটি স্তম্ভের ছায়ার দৈর্ঘ্য স্তম্ভের উচ্চতা থেকে কম।

উত্তরঃ যখন সূর্যের উন্নতি কোণ 45°-এর বেশি তখন একটি স্তম্ভের ছায়ার দৈর্ঘ্য স্তম্ভের উচ্চতা থেকে কম।

Koshe Dekhi 25 Class 10

Q25. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)

(i) একটি ঘুডির উন্নতি কোণ 60° এবং সুতোর দৈর্ঘ্য 20√3 মিটার হলে, ঘুড়িটি মাটি থেকে কত উচ্চতায় আছে হিসাব করি।

সমাধানঃ

koshe dekhi 25_class 10

ধরি, ঘুড়িটি মাটি থেকে AB উচ্চতায় উড়ছে (যার দৈর্ঘ্য আমাদের নির্ণয় করতে হবে)।

এখন, সমকোণী ত্রিভুজ ABC থেকে ∠ACB -এর সাপেক্ষে পাই –

sin ∠ACB = লম্ব / অতিভুজ

বা, $sin60^{\circ}=\frac{AB}{AC}$ [যেহেতু, ∠ACB = 60°]

বা, $\frac{\sqrt{3}}{2}=\frac{AB}{20\sqrt{3}}$ [যেহেতু, ${\color{Blue} sin60^{\circ}=\frac{\sqrt{3}}{2}}$ ]

বা, $2AB=20\times \sqrt{3}\times \sqrt{3}=60$

বা, $AB=\frac{60}{2}=30$

∴ AB = 30 মিটার

উত্তরঃ নির্ণেয় ঘুড়িটি মাটি থেকে 30 মিটার উচ্চতায় উড়ছিল।

Koshe Dekhi 25 Class 10

Q25. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)

(ii) একটি সমকোণী ত্রিভুজাকারক্ষেত্র ABC-এর অতিভুজ AC-এর দৈর্ঘ্য 100 মিটার এবং AB = 50√3 মিটার হলে, ∠C -এর মান নির্ণয় করি।

সমাধানঃ

koshe dekhi 25_class 10

সমকোণী ত্রিভুজ ABC থেকে ∠C -এর সাপেক্ষে পাই –

sin ∠C = লম্ব / অতিভুজ

বা, $sin\angle C=\frac{AB}{AC}$

বা, $sin\angle C=\frac{50\sqrt{3}}{100}$

বা, $sin\angle C=\frac{\sqrt{3}}{2}$

∴ ∠C = 60° [যেহেতু, ${\color{Blue} sin60^{\circ}=\frac{\sqrt{3}}{2}}$ ]

উত্তরঃ নির্ণেয় ∠C -এর মান 60°

Koshe Dekhi 25 Class 10

Q25. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)

(iii) ঝড়ে একটি গাছ মচকে গিয়ে তার অগ্রভাগ এমনভাবে ভূমি স্পর্শ করেছে যে গাছটির অগ্রভাগ থেকে গোড়ার দূরত্ব এবং বর্তমান উচ্চতা সমান। গাছটির অগ্রভাগ ভূমির সাথে কত কোণ করেছে হিসাব করি।

সমাধানঃ

koshe dekhi 25_class 10

ধরি, BD গাছটি A বিন্দু থেকে মচকে গিয়ে তার অগ্রভাগ (অর্থাৎ, বিন্দু D) ভূমির C বিন্দুতে স্পর্শ করেছে।

এক্ষেত্রে, AB হলো গাছটির বর্তমান উচ্চতা এবং BC হলো গাছটির গোড়া থেকে অগ্রভাগের দূরত্ব।

প্রশ্নানুসারে, AB = BC

ΔABC থেকে ∠ACB -এর সাপেক্ষে পাই –

tan ∠ACB = লম্ব / ভূমি

বা, $tan\angle ACB=\frac{AB}{BC}$

বা, $tan\angle ACB=\frac{AB}{AB}=1$ [যেহেতু, AB = AC ]

∴ ∠ACB = 45° [যেহেতু, ${\color{Blue} tan45^{\circ}=1}$ ]

উত্তরঃ নির্ণেয় গাছটির অগ্রভাগ ভূমির সাথে 45° কোণ করেছে।

Koshe Dekhi 25 Class 10

Q25. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)

(iv) ABC সমকোণী ত্রিভুজ ∠B = 90°, AB -এর উপর D এমন একটি বিন্দু যে, AB : BC : BD = √3 : 1 : 1, ∠ACD -এর মান নির্ণয় করি।

সমাধানঃ

koshe dekhi 25_class 10

ধরি, AB = √3k , BC = k এবং BD = k (যেখানে k ≠ 0)

এখন, ΔABC থেকে ∠ACB -এর সাপেক্ষে পাই –

tan ∠ACB = লম্ব / ভূমি

বা, $tan\angle ACB=\frac{AB}{BC}$

বা, $tan\angle ACB=\frac{\sqrt{3}k}{k}=\sqrt{3}$

∴ ∠ACB = 60° [যেহেতু, ${\color{Blue} tan60^{\circ}=\sqrt{3}}$ ]

আবার,

ΔDBC থেকে ∠DCB -এর সাপেক্ষে পাই –

tan ∠DCB = লম্ব / ভূমি

বা, $tan\angle DCB=\frac{DB}{BC}$

বা, $tan\angle DCB=\frac{k}{k}=1$

∴ ∠DCB = 45° [যেহেতু, ${\color{Blue} tan45^{\circ}=1}$ ]

এখন, ∠ACD = ∠ACB − ∠DCB

বা, ∠ACD = 60° − 45°

∴ ∠ACD = 15°

উত্তরঃ নির্ণেয় ∠ACD -এর মান হলো 15°

Koshe Dekhi 25 Class 10

Q25. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)

(v) একটি স্তম্ভের ছায়ার দৈর্ঘ্য এবং স্তম্ভের উচ্চতার অনুপাত √3 : 1 হলে, সূর্যের উন্নতি কোণ নির্ণয় করি৷

সমাধানঃ

koshe dekhi 25 class 10

যেহেতু প্রদত্ত আছে, স্তম্ভের ছায়ার দৈর্ঘ্য এবং স্তম্ভের উচ্চতার অনুপাত √3 : 1

∴ ধরি, সূর্যের উন্নতি কোণ যখন ∠ACB তখন স্তম্ভের ছায়ার দৈর্ঘ্য = BC = √3k এবং

AB = স্তম্ভের উচ্চতা = k

(যেখানে k ≠ 0)

এখন, ΔABC থেকে ∠ACB -এর সাপেক্ষে পাই –

tan ∠ACB = লম্ব / ভূমি

বা, $tan\angle ACB=\frac{AB}{BC}$

বা, $tan\angle ACB=\frac{k}{\sqrt{3}k}=\frac{1}{\sqrt{3}}$

∴ ∠ACB = 30° [যেহেতু, ${\color{Blue} tan30^{\circ}=\frac{1}{\sqrt{3}}}$ ]

উত্তরঃ নির্ণেয় সূর্যের উন্নতি কোণ 30°

Koshe Dekhi 25 Class 10

Support Me

If you like my work then you can Support me by contributing a small amount which will help me a lot to grow my Website. It’s a request to all of you. You can donate me through phone pay / Paytm/ Gpay on this number 7980608289 or by the link below :

and visit Our website : learningscience.co.in

গণিত প্রকাশ (দশম শ্রেণী) সম্পূর্ণ সমাধান

গণিত প্রকাশ (নবম শ্রেণী) সম্পূর্ণ সমাধান

গণিত প্রভা (ষষ্ঠ শ্রেণী) সম্পূর্ণ সমাধান

জীবন বিজ্ঞান (দশম শ্রেণী) (Life Science)

Thank You