Koshe Dekhi 26.1 Class 10

Q.1) আমি আমার 40 জন বন্ধুর বয়স নিচের ছকে লিখছি,

বয়স (বছর)	15	16	17	18	19	20
বন্ধুর সংখ্যা	4	7	10	10	5	4

আমি আমার বন্ধুদের গড় বয়স প্রত্যক্ষ পদ্ধতিতে নির্ণয় করি।

সমাধানঃ

মধ্যমা 26.1

∴ আমার বন্ধুদের গড় বয়স $=\frac{\sum x_{i}f_{i}}{\sum f_{i}}$ $=\frac{697}{40}$ বছর = 17.425 বছর = 17.43 বছর (প্রায়) .

উত্তরঃ নির্ণেয় প্রত্যক্ষ পদ্ধতিতে আমার 40 জন বন্ধুর গড় বয়স 17.43 বছর (প্রায়)।

Q.2) গ্রামের 50 টি পরিবারের সদস্য সংখ্যা নীচের তালিকায় লিখেছি :

সদস্য সংখ্যা	2	3	4	5	6	7
পরিবারের সংখ্যা	6	8	14	15	4	3

ওই 50 টি পরিবারের গড় সদস্য সংখ্যা কল্পিত গড় পদ্ধতিতে লিখি।

সমাধানঃ

মধ্যমা 26.1

ধরি, কল্পিত গড় (a ) = 5

কল্পিত গড় পদ্ধতিতে 50 টি পরিবারের গড় সদস্য সংখ্যা

= a + $\frac{\sum f_{i}d_{i}}{\sum f_{i}}$

$=5+\left ( \frac{-38}{50} \right )$

$=5-\frac{19}{25}$

$=\frac{125-19}{25}$

$=\frac{106}{25}$

= 4.24

উত্তরঃ নির্ণেয় কল্পিত গড় পদ্ধতিতে 50 টি পরিবারের গড় সদস্য সংখ্যা 4.24 জন।

Q.3) যদি নীচের প্রদত্ত তথ্যের যৌগিক গড় 20.6 হয়, তবে a এর মান নির্ণয় করি :

চল $\left ( x_{i} \right )$	10	15	a	25	35
পরিসংখ্যা $\left ( f_{i} \right )$	3	10	25	7	5

সমাধানঃ

কষে দেখি 26.1

প্রদত্ত যৌগিক গড় 20.6

প্রশ্নানুসারে,

বা, $\frac{530+25a}{50}=20.6$

বা, 530 + 25a = 1030

বা, 25a = 1030 – 530

বা, 25a = 500

বা, $a=\frac{500}{25}$

∴ a = 20

উত্তরঃ নির্ণেয় a এর মান 20

Q.4) যদি নীচের প্রদত্ত তথ্যের যৌগিক গড় 15 হয়, তবে p -এর মান হিসাব করে লিখি :

চল	5	10	15	20	25
পরিসংখ্যা	6	p	6	10	5

সমাধানঃ

মধ্যমা 26.1

প্রদত্ত যৌগিক গড় 15

প্রশ্নানুসারে,

বা, $\frac{445+10p}{27+p}=15$

বা, 445 + 10p = 405 + 15p

বা, 445 – 405 = 15p – 10p

বা, 5p = 40

বা, $p=\frac{40}{5}$

∴ p = 8

উত্তরঃ নির্ণেয় p এর মান 8

Q.5) রহমতচাচা তার 50 টি বাক্সে বিভিন্ন সংখ্যায় আম ভরে পাইকারি বাজারে নিয়ে যাবেন। কতগুলি বাক্সে কতগুলি আম রাখলেন তার তথ্য নীচের ছকে লিখলাম।

আমের সংখ্যা	50 – 52	52 – 54	54 – 56	56 – 58	58 – 60
বাক্সের সংখ্যা	6	14	16	9	5

আমি ওই 50টি বাক্সে গড় আমের সংখ্যা হিসাব করে লিখি। (যে-কোনো পদ্ধতিতে)

সমাধানঃ

মধ্যমা 26.1

∴ প্রত্যক্ষ পদ্ধতিতে 50টি বাক্সে গড় আমের সংখ্যা $=\frac{\sum f_{i}x_{i}}{\sum f_{i}}=\frac{2736}{50}=54.72$ টি।

উত্তরঃ নির্ণেয় রহমতচাচার 50টি বাক্সে গড় আমের সংখ্যা 54.72 টি।

Q.6) মহিদুল পাড়ার হাসপাতালের 100 জন রোগীর বয়স নীচের ছকে লিখল। ওই 100 জন রোগীর গড় বয়স হিসাব করে লিখি। (যে-কোনো পদ্ধতিতে)

বয়স (বছরে)	10 – 20	20 – 30	30 – 40	40 – 50	50 – 60	60 – 70
রোগীর সংখ্যা	12	8	22	20	18	20

সমাধানঃ

মধ্যমা 26.1

∴ প্রত্যক্ষ পদ্ধতিতে 100 জন রোগীর গড় বয়স $=\frac{\sum f_{i}x_{i}}{\sum f_{i}}=\frac{4340}{100}=43.4$ বছর।

উত্তরঃ নির্ণেয় প্রত্যক্ষ পদ্ধতিতে 100 জন রোগীর গড় বয়স 43.4 বছর।

Q.7) প্রত্যক্ষ পদ্ধতিতে নীচের তথ্যের গড় নির্ণয় করি :

(i)

শ্রেণী-সীমানা	0 – 10	10 – 20	20 – 30	30 – 40	40 – 50
পরিসংখ্যা	4	6	10	6	4

সমাধানঃ

রাশিবিজ্ঞান কষে দেখি - 26.1

আমরা জানি, যৌগিক গড়, $\overline{x}=\frac{\sum f_{i}x_{i}}{\sum f_{i}}$ [প্রত্যক্ষ পদ্ধতি]

$\therefore \overline{x}=\frac{750}{30}$

=25

উত্তরঃ নির্ণেয় তথ্যের যৌগিক গড় 25

Q.7) প্রত্যক্ষ পদ্ধতিতে নীচের তথ্যের গড় নির্ণয় করি :

(ii)

শ্রেণী-সীমানা	10 – 20	20 – 30	30 – 40	40 – 50	50 – 60	60 – 70
পরিসংখ্যা	10	16	20	30	13	11

সমাধানঃ

রাশিবিজ্ঞান কষে দেখি - 26.1

আমরা জানি, যৌগিক গড়, $\overline{x}=\frac{\sum f_{i}x_{i}}{\sum f_{i}}$ [প্রত্যক্ষ পদ্ধতি]

$\therefore \overline{x}=\frac{4030}{100}$

=40.3

উত্তরঃ নির্ণেয় তথ্যের যৌগিক গড় 40.3

Koshe Dekhi 26.1 Class 10

Q.8) কল্পিত গড় পদ্ধতিতে নীচের তথ্যের গড় নির্ণয় করি :

(i)

শ্রেণী-সীমানা	0 – 40	40 – 80	80 – 120	120 – 160	160 – 200
পরিসংখ্যা	12	20	25	20	13

সমাধানঃ

রাশিবিজ্ঞান কষে দেখি - 26.1

আমরা জানি, যৌগিক গড়, $\overline{x}=a+\frac{\sum f_{i}d_{i}}{\sum f_{i}}$ [কল্পিত গড় পদ্ধতি]

$\therefore \overline{x}=100+\left (\frac{80}{90} \right )$

$=100+\left ( \frac{8}{9} \right )$

=100+0.888 (প্রায়)

=100.888 (প্রায়)

=100.89 (প্রায়)

উত্তরঃ নির্ণেয় তথ্যের যৌগিক গড় 100.89 (প্রায়)

Koshe Dekhi 26.1 Class 10

Q.8) কল্পিত গড় পদ্ধতিতে নীচের তথ্যের গড় নির্ণয় করি :

(ii)

শ্রেণী-সীমানা	25 – 35	35 – 45	45 – 55	55 – 65	65 – 75
পরিসংখ্যা	4	10	8	12	6

সমাধানঃ

রাশিবিজ্ঞান কষে দেখি - 26.1

আমরা জানি, যৌগিক গড়, $\overline{x}=a+\frac{\sum f_{i}d_{i}}{\sum f_{i}}$ [কল্পিত গড় পদ্ধতি]

$\therefore \overline{x}=50+\left (\frac{60}{40} \right )$

$=50+\left ( \frac{3}{2} \right )$

=50+1.5

=51.5

উত্তরঃ নির্ণেয় তথ্যের যৌগিক গড় 51.5

Koshe Dekhi 26.1 Class 10

Q.9) ক্রম বিচ্যুতি পদ্ধতিতে নীচের তথ্যের গড় নির্ণয় করি :

(i)

শ্রেণী-সীমানা	0 – 30	30 – 60	60 – 90	90 – 120	120 – 150
পরিসংখ্যা	12	15	20	25	8

সমাধানঃ

ধরি, a = 75

এখানে, শ্রেণি দৈর্ঘ্য (h) = 30 − 0 = 60− 30 = 90− 60 = … = 150 − 120 = 30

মধ্যমা 26.1

∴ ক্রম বিচ্যুতি পদ্ধতিতে প্রদত্ত তথ্যের গড়,

$\bar{x}=a+\left ( \frac{\sum f_{i}u_{i}}{\sum f_{i}} \right )\times h$

$=75+\frac{2}{80}\times 30$

$=75+\frac{3}{4}$

=75+0.75

=75.75

উত্তরঃ নির্ণেয় ক্রম বিচ্যুতি পদ্ধতিতে প্রদত্ত তথ্যের গড় 75.75

Koshe Dekhi 26.1 Class 10

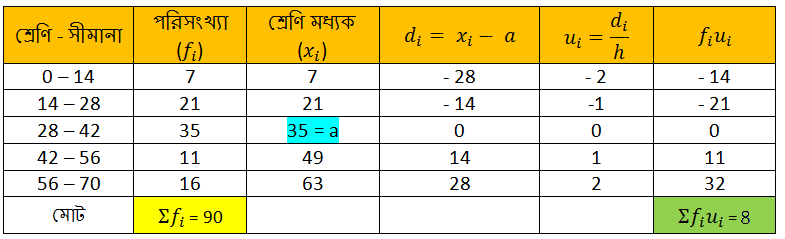
Q.9) ক্রম বিচ্যুতি পদ্ধতিতে নীচের তথ্যের গড় নির্ণয় করি :

(ii)

শ্রেণী-সীমানা	0 – 14	14 – 28	28 – 42	42 – 56	56 – 70
পরিসংখ্যা	7	21	35	11	16

সমাধানঃ

ধরি, a = 35

এখানে, শ্রেণি দৈর্ঘ্য (h) = 14 − 0 = 28− 14 = 42− 28 = … = 70 − 56 = 14

koshe dekhi-26.1

∴ ক্রম বিচ্যুতি পদ্ধতিতে প্রদত্ত তথ্যের গড়,

$\bar{x}=a+\left ( \frac{\sum f_{i}u_{i}}{\sum f_{i}} \right )\times h$

$=35+\frac{8}{90}\times 14$

$=35+\frac{56}{45}$

=35+1.24444 (প্রায়)

=36.24 (প্রায়)

উত্তরঃ নির্ণেয় ক্রম বিচ্যুতি পদ্ধতিতে প্রদত্ত তথ্যের গড় 35.31 (প্রায়) .

Koshe Dekhi 26.1 Class 10

Q.10) যদি নীচের পরিসংখ্যা তালিকা বিভাজন তালিকার নম্বরের যৌগিক গড় 24 হয়, তবে p -এর মান নিৰ্ণয় করি :

শ্রেণী-সীমানা (নম্বর)	0 – 10	10 – 20	20 – 30	30 – 40	40 – 50
ছাত্রসংখ্যা	15	20	35	p	10

সমাধানঃ

মধ্যমা 26.1

প্রদত্ত, যৌগিক গড় 24

প্রশ্নানুসারে,

বা, $\frac{1700+35p}{80+p}=24$

বা, 1700 + 35p = 1920 + 24p

বা, 35p – 24p = 1920 – 1700

বা, 11p = 220

বা, $p=\frac{220}{11}$

∴ p = 20

উত্তরঃ নির্ণেয় p এর মান 20

Koshe Dekhi 26.1 Class 10

Q.11) আলোচনা সভায় উপস্থিত ব্যাক্তিদের বয়সের তালিকা দেখি ও গড় বয়স নির্ণয় করি :

বয়স (বছর)	30 – 34	35 – 39	40 – 44	45 – 49	50 – 54	55 – 59
রোগীর সংখ্যা	10	12	15	6	4	3

সমাধানঃ

মধ্যমা 26.1

∴ প্রত্যক্ষ পদ্ধতিতে, 50 জন রোগীর গড় বয়স $\bar{x}=\frac{\sum f_{i}x_{i}}{\sum f_{i}}=\frac{2055}{50}=41.1$ বছর।

উত্তরঃ নির্ণেয় 50 জন রোগীর গড় বয়স 41.1 বছর।

Koshe Dekhi 26.1 Class 10

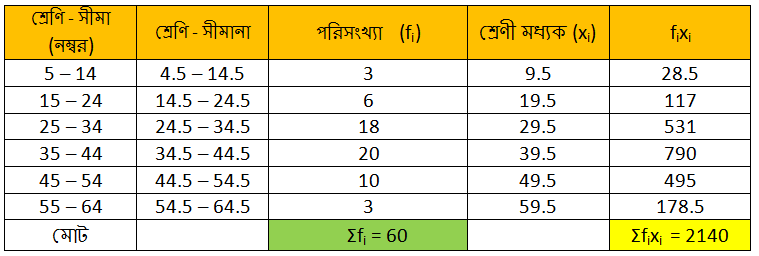
Q.12) নীচের তথ্যের গড় নির্ণয় করি :

শ্রেণী-সীমা	5 – 14	15 – 24	25 – 34	35 – 44	45 – 54	55 – 64
পরিসংখ্যা	3	6	18	20	10	3

সমাধানঃ

মধ্যমা 26.1

∴ প্রত্যক্ষ পদ্ধতিতে, 60 জনের গড় নম্বর $\bar{x}=\frac{\sum f_{i}x_{i}}{\sum f_{i}}=\frac{2140}{60}=35.666$ (প্রায়)

= 35.67 (প্রায়)।

উত্তরঃ নির্ণেয় 60 জনের গড় নম্বর 35.67 (প্রায়)।

Koshe Dekhi 26.1 Class 10

Q.13) ছাত্রীদের প্রাপ্ত নম্বরের গড় নির্ণয় করি, যদি তাদের প্রাপ্ত নম্বরের ক্রোমযৌগিক পরিসংখ্যা নিম্নরূপ হয় :

শ্রেণী-সীমা (নম্বর)	10 এর কম	20 এর কম	30 এর কম	40 এর কম	50 এর কম
ছাত্রীসংখ্যা	5	9	17	29	45

সমাধানঃ

প্রথমে প্রদত্ত তালিকাটিকে সাধারন বিভাজন তালিকায় প্রকাশ করি,

এখানে, 5 জন 10-এর কম পেয়েছে।

অর্থাৎ, (0 – 10) – এর মধ্যে পেয়েছে 5 জন।

আবার, 9 জন 20 -এর কম পেয়েছে।

অর্থাৎ, (10 – 20) -এর মধ্যে পেয়েছে ( 9 – 5 ) জন = 4 জন।

সুতরাং,পরিসংখ্যা তালিকাটি হবে

মধ্যমা 26.1

∴ প্রত্যক্ষ পদ্ধতিতে, 45 জন ছাত্রীর প্রাপ্ত নম্বরের গড়, $\bar{x}=\frac{\sum f_{i}x_{i}}{\sum f_{i}}=\frac{1425}{45}=31.666$ (প্রায়)

= 31.67 (প্রায়)।

উত্তরঃ নির্ণেয় 45 জন ছাত্রীর প্রাপ্ত নম্বরের গড় 31.67 (প্রায়)।

Koshe Dekhi 26.1 Class 10

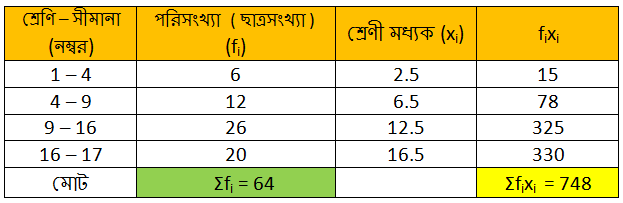
Q.14) নীচের তালিকার 64 জন ছাত্রের প্রাপ্ত নম্বরের গড় নির্ণয় করি।

শ্রেণী-সীমা (নম্বর)	1 – 4	4 – 9	9 – 16	16 – 17
ছাত্রসংখ্যা	6	12	26	20

সমাধানঃ

মধ্যমা 26.1

∴ প্রত্যক্ষ পদ্ধতিতে, 46 জন ছাত্রের প্রাপ্ত নম্বরের গড়, $\bar{x}=\frac{\sum f_{i}x_{i}}{\sum f_{i}}=\frac{748}{64}=11.6875$ (প্রায়)

= 11.69 (প্রায়)।

উত্তরঃ নির্ণেয় 64 জন ছাত্রের প্রাপ্ত নম্বরের গড় 11.69 (প্রায়)।

Koshe Dekhi 26.1 Class 10

Thank You

5 thoughts on “Koshe Dekhi 26.1 Class 10”

Saswati Paul
January 17, 2023 at 6:42 pm
This is very helpful..
Thanks for your support…
- Prasanta Naskar
  January 17, 2023 at 10:48 pm
  You are welcome.
  Please share with your friends and keep visiting.
  Thanks and Regards.
  - Aditya Srivastava
    June 24, 2023 at 5:47 pm
    It is very helpful
    - Prasanta Naskar
      June 28, 2023 at 8:27 pm
      Thank you
Krishnendu Kumar Bose
October 1, 2023 at 7:22 am
Thank you so much to help me by this .

Koshe Dekhi 26.1 Class 10

Koshe Dekhi 26.1 Class 10

5 thoughts on “Koshe Dekhi 26.1 Class 10”

Leave a Comment Cancel reply