Koshe dekhi 3 Class 8

(d) \(5m − 3 = 0\)

সমাধানঃ

\(\begin{array}{l}5m-3=0\\\Rightarrow 5m=3\\\therefore m=\frac{3}{5}\end{array}\)

\(\therefore \) নির্ণেয় সমীকরণের বীজটি হলো : \(\frac{3}{5} \)

এবং সমীকরণটির সমাধান হলো, \(m =\frac{3}{5} \)

(e) \(9y + 18 = 0\)

সমাধানঃ

\(\begin{array}{l}9y+18=0\\\Rightarrow 9y=-18\\\Rightarrow y=\frac{{-18}}{9}\\\therefore y=\frac{-2}{1}\end{array}\)

\(\therefore \) নির্ণেয় সমীকরণের বীজটি হলো : \(\frac{-2}{1} \)

এবং সমীকরণটির সমাধান হলো, \(y =-2 \)

(f) \(t = 8 − 12t\)

সমাধানঃ

\(\begin{array}{l}t=8-12t\\\Rightarrow t+12t=8\\\Rightarrow 13t=8\\\therefore t=\frac{8}{{13}}\end{array}\)

\(\therefore \) নির্ণেয় সমীকরণের বীজটি হলো : \(\frac{8}{13} \)

এবং সমীকরণটির সমাধান হলো, \(t =\frac{8}{13} \)

(g) \(6y = 5 + y\)

সমাধানঃ

\(\begin{array}{l}6y=5+y\\\Rightarrow 6y-y=5\\\Rightarrow 5y=5\\\Rightarrow y=\frac{5}{5}\\\therefore y=\frac{1}{1}\end{array}\)

\(\therefore \) নির্ণেয় সমীকরণের বীজটি হলো : \(\frac{1}{1} \)

এবং সমীকরণটির সমাধান হলো, \(y =1 \)

(h) \(2x +\) ____ = ____ [নিজে মূলদ সংখ্যা বসাই]

সমাধানঃ

আমি প্রথম শূন্যস্থানে \(12 \) এবং দ্বিতীয় শূন্যস্থানে \( 2 \) বসলাম। সুতরাং, সমীকরণটি হলো ,

\( \begin{array}{l}2x+12=2\\\Rightarrow 2x=2-12\\\Rightarrow 2x=-10\\\Rightarrow x=\frac{{-10}}{2}\\\therefore x=\frac{{-5}}{1}\end{array} \)

\(\therefore \) নির্ণেয় সমীকরণের বীজটি হলো : \(\frac{-5}{1} \)

এবং সমীকরণটির সমাধান হলো, \(x =-5 \)

আরও দেখুনঃ

2. \(y=- \frac{5}{4} \) হলে, \( − (– y) = y \) যাচাই করি।

সমাধানঃ

\( y=-\frac{5}{4}\) হলে,

বামপক্ষ:
\( \begin{array}{l}=-(-y) \\ =-\left\{-\left(-\frac{5}{4}\right)\right\} \\ =-\frac{5}{4} \\ =-\frac{5}{4} \end{array} \)
\(=y = \) ডানপক্ষ (প্রমাণিত)

3. \(x=- \frac{3}{8} \) হলে, মান খুঁজি

(a) \(2x + 5\)

সমাধানঃ

\(x=- \frac{3}{8} \) হলে,

\( \begin{array}{l}2x+5\\=2\times \left( {-\frac{3}{8}} \right)+5\\=\left( {-\frac{3}{4}} \right)+5\\=\left( {-\frac{3}{4}} \right)+\frac{{5\times 4}}{4}\\=\left( {-\frac{3}{4}} \right)+\frac{{20}}{4}\\=\frac{{20-3}}{4}\\=\frac{{17}}{4}\end{array}\)

(b) \( x+ \frac{3}{8} \)

সমাধানঃ

\(x=- \frac{3}{8} \) হলে,

\( \begin{array}{l}x+\frac{3}{8}\\=\left( {-\frac{3}{8}} \right)+\frac{3}{8}\\=0\end{array}\)

সমাধানঃ

\(x=- \frac{3}{8} \) হলে,

\( \begin{array}{l}5-\left( {-x} \right)\\=5+x\\=5+\left( {-\frac{3}{8}} \right)\\=\frac{{5\times 8}}{8}-\frac{3}{8}\\=\frac{{40}}{8}-\frac{3}{8}\\=\frac{{40-3}}{8}\\=\frac{{37}}{8}\\=4\frac{5}{8}\end{array}\)

(d) ____ \(− (−x) \) [নিজে মূলদ সংখ্যা বসাই]

সমাধানঃ

আমি শূন্যস্থানে \(4\) বসিয়ে সংখ্যামালাটির মান খুঁজি, যেখানে \(x=- \frac{3}{8} \)

\( \begin{array}{l}4-\left( {-x} \right)\\=4+x\\=4+\left( {-\frac{3}{8}} \right)\\=\frac{{4\times 8}}{8}-\frac{3}{8}\\=\frac{{32}}{8}-\frac{3}{8}\\=\frac{{32-3}}{8}\\=\frac{{29}}{8}\\=3\frac{5}{8}\end{array}\)

আরও দেখুনঃ

4. নীচের ফাঁকা ঘরে বুঝে সংখ্যা লিখি :

(a) \(\frac{9}{11} \) + ____ = 0

সমাধানঃ

আমরা জানি, দুটি বিপরীত চিহ্নযুক্ত সমান সংখ্যার যোগফল সর্বদা \(0 \) হয়।

\(\therefore \) \(\frac{9}{11} + (-\frac{9}{11} ) =0\)

উত্তরঃ শূন্যস্থানে যে সংখ্যাটি হবে সেটি হলো = \((-\frac{9}{11} ) \)

(b) ____ + \( (-\frac{21}{29} )\) = 0

সমাধানঃ

আমরা জানি, দুটি বিপরীত চিহ্নযুক্ত সমান সংখ্যার যোগফল সর্বদা \(0 \) হয়।

\(\therefore \) \(\frac{21}{29} + (-\frac{21}{29} ) =0\)

উত্তরঃ শূন্যস্থানে যে সংখ্যাটি হবে সেটি হলো = \(\frac{21}{29} \)

সমাধানঃ

আমরা জানি, পরস্পর দুটি অনোন্যক সংখ্যার গুনফল সর্বদা \(1 \) হয়।

\(\therefore \) \(\frac{7}{19}\times (\frac{19}{7} ) =1\)

উত্তরঃ শূন্যস্থানে যে সংখ্যাটি হবে সেটি হলো = \(\frac{19}{7} \)

(d) − 5 × ____ = 1

সমাধানঃ

আমরা জানি, পরস্পর দুটি অনোন্যক সংখ্যার গুনফল সর্বদা \(1 \) হয়।

\(\therefore \) \((-5) \times (-\frac{1}{5} ) =1\)

উত্তরঃ শূন্যস্থানে যে সংখ্যাটি হবে সেটি হলো = \((-\frac{1}{5}) \)

(e) \(-\frac{15}{23}\) × _____ = 1

সমাধানঃ

আমরা জানি, পরস্পর দুটি অনোন্যক সংখ্যার গুনফল সর্বদা \(1 \) হয়।

\(\therefore \) \((-\frac{15}{23} ) \times (-\frac{23}{15} ) =1\)

উত্তরঃ শূন্যস্থানে যে সংখ্যাটি হবে সেটি হলো = \((-\frac{23}{15}) \)

(f) \(\left( {-\frac{8}{3}} \right)\times \left( {-\frac{{21}}{{20}}} \right)\) = _____

সমাধানঃ

\(\begin{array}{l}\left( {-\frac{8}{3}} \right)\times \left( {-\frac{{21}}{{20}}} \right)\\=\frac{8}{3}\times \frac{{21}}{{20}}\\=\frac{{4\times 2\times 3\times 7}}{{3\times 4\times 5}}\\=\frac{{2\times 7}}{5}\\=\frac{{14}}{5}\\=2\frac{4}{5}\end{array}\)

উত্তরঃ শূন্যস্থানে যে সংখ্যাটি হবে সেটি হলো = \(2\frac{4}{5} \)

5. \(\frac{7}{18} \) -কে \( (-\frac{5}{6} )\) -এর অন্যোন্যক দিয়ে গুণ করে গুণফল লিখি।

সমাধানঃ

\( (-\frac{5}{6})\) -এর অন্যোন্যক হলো \( (-\frac{6}{5})\)

\( \therefore \quad \frac{7}{18} \times\left(-\frac{6}{5}\right)\)

\( =-\left(\frac{7}{18} \times \frac{6}{5}\right) \)

\( =-\frac{7}{15} \)

আরও দেখুনঃ

6. বিনিময় ও সংযোগ নিয়মের সাহায্যে মান খুঁজি :

(i) (i) \( \frac{5}{8}+\left(-\frac{7}{15}\right)+\left(\frac{3}{32}\right)+\frac{11}{75} \)

সমাধানঃ

\(\frac{5}{8}+\left(-\frac{7}{15}\right)+\left(\frac{3}{32}\right)+\frac{11}{75} \)
\(=\frac{5}{8}+\left\{\left(-\frac{7}{15}\right)+\left(\frac{3}{32}\right)\right\}+\frac{11}{75} \)
\(=\frac{5}{8}+\left\{\left(\frac{3}{32}\right)+\left(-\frac{7}{15}\right)\right\}+\frac{11}{75} \) [যোগের বিনিময় নিয়মের সাহায্যে পাই]
\(=\left\{\frac{5}{8}+\left(\frac{3}{32}\right)\right\}+\left\{\left(-\frac{7}{15}\right)+\frac{11}{75}\right\}\) [যোগের সংযোগ নিয়মের সাহায্যে পাই]
\(=\left\{ {\frac{{5\times 4}}{{8\times 4}}+\frac{3}{{32}}} \right\}+\left\{ {-\frac{{7\times 5}}{{15\times 5}}+\frac{{11}}{{75}}} \right\}\)
\(=\left\{ {\frac{{20}}{{32}}+\frac{3}{{32}}} \right\}+\left\{ {-\frac{{35}}{{75}}+\frac{{11}}{{75}}} \right\}\)
\(=\left\{ {\frac{{20+3}}{{32}}} \right\}+\left\{ {\frac{{-35+11}}{{75}}} \right\}\)
\(=\frac{{23}}{{32}}+\left( {\frac{{-24}}{{75}}} \right)\)
\(=\frac{{23\times 75-24\times 32}}{{32\times 75}}\)
\(=\frac{{1725-768}}{{32\times 75}}\)
\(=\frac{{957}}{{32\times 75}}\)
\(=\frac{{3\times 319}}{{32\times 25\times 3}}\)
\(=\frac{{319}}{{32\times 25}}\)
\(=\frac{{319}}{{800}}\)

(ii) \( \frac{8}{121} \times \frac{35}{169} \times \frac{55}{36} \times \frac{78}{49} \)

সমাধানঃ

\( \frac{8}{121} \times \frac{35}{169} \times \frac{55}{36} \times \frac{78}{49} \)
\(=\frac{8}{121} \times\left(\frac{35}{169} \times \frac{55}{36}\right) \times \frac{78}{49}\)
\(=\frac{8}{121} \times\left(\frac{55}{36} \times \frac{35}{169}\right) \times \frac{78}{49} \) [গুনের বিনিময় নিয়মের সাহায্যে পাই]
\(=\left(\frac{8}{121} \times \frac{55}{36}\right) \times\left(\frac{35}{169} \times \frac{78}{49}\right) \) [গুনের সংযোগ নিয়মের সাহায্যে পাই]
\( =\frac{10}{99} \times \frac{30}{91} \)
\(=\frac{100}{3003}\)

7. সংখ্যারেখায় মূলদ সংখ্যাগুলি বসাই :

\( \frac{1}{4}, -\frac{3}{4}, -\frac{2}{3}, \frac{6}{5}, -\frac{8}{3} \)

সমাধানঃ

\( \frac{1}{4}\)

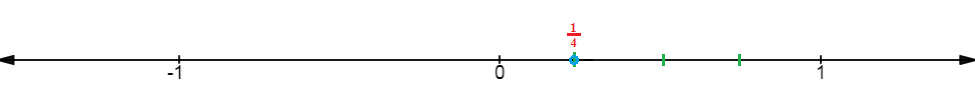
koshe dekhi 3 class 8

\( -\frac{3}{4}\)

koshe dekhi 3 class 8

\( -\frac{2}{3}\)

koshe dekhi 3 class 8

\( \frac{6}{5}\)

koshe dekhi 3 class 8

\( -\frac{8}{3}\)

koshe dekhi 3 class 8

আরও দেখুনঃ