Koshe dekhi 20.1 Class 8

Koshe dekhi 20.1 Class 8

1. ΔABC এর BC বাহুর উপর D যেকোনো একটি বিন্দু। প্রমাণ করি যে, AB + BC + CA > 2AD

সমাধানঃ 

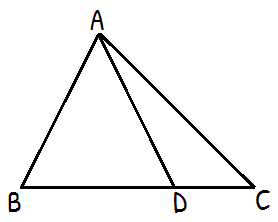
প্রদত্তঃ ∆ABC এর BC বাহুর উপর D যেকোনো একটি বিন্দু।

প্রামাণ্যঃ AB + BC + CA > 2AD

প্রমাণঃ
ΔABD থেকে পাই, AB + BD > AD ……. (i)
ΔADC থেকে পাই, DC + AC > AD ……. (ii)

(i) নং ও (ii) নং সমীকরণ যোগ করে পাই,
AB + BD + DC + AC > AD + AD
বা, AB + (BD + DC) + AC > 2AD
∴ AB + BC + CA > 2AD  [প্রমাণিত]

2. ΔABC এর ভিতরে O যেকোনো একটি বিন্দু। প্রমাণ করি যে,
(i) AB + AC > OB + OC
(ii) AB + BC + AC > OA + OB + OC

সমাধানঃ 

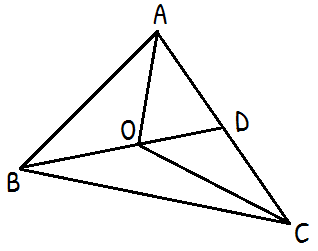
প্রদত্তঃ ΔABC এর ভিতবে O যেকোনো একটি বিন্দু।

প্রামাণ্যঃ
(1) AB + AC > OB + OC
(2) AB + BC + AC > OA + OB + OC

প্রমাণঃ
△ABD থেকে পাই,  AB + AD > BD 
বা, AB + AD > BO + OD …….(i)

ΔOCD থেকে পাই,
OD + DC > OC ……(ii)

(i) নং ও (ii) নং যোগ করে পাই,
AB + AD + OD + DC > BO + OD + OC
বা, AB + (AD + DC) > BO + OC
∴ AB + AC > BO + OC ……(iii)  [(1) নং প্রমাণিত]

অনুরূপে প্রমাণ করা যায় যে,
AB + BC > OA + OC ……(iv) এবং 
AC + BC > OA + OB ……(v)

(iii)+(iv)+(v) করে পাই,
AB + AC + AB + BC + AC + BC > OB + OC + OA + OC + OA + OB
বা, 2(AB + BC + AC) > 2(OA + OB + OC)
∴ AB + BC + AC > OA + OB + OC  [(2) নং প্রমাণিত]

3. প্রমাণ করি যে, একটি চতুর্ভুজের পরিসীমা যেকোনো কর্ণের দৈর্ঘ্যের দ্বিগুণ অপেক্ষা বৃহত্তর।

সমাধানঃ 

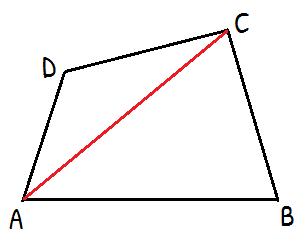
প্রদত্তঃ ABCD একটি চতুর্ভুজ। AC চতুর্ভুজের যেকোনো একটি কর্ণ।

প্রামাণ্যঃ AB + BC + CD + DA > 2AC

প্রমাণঃ
∆ABC থেকে পাই, AB + BC > AC ……(i)
ΔADC থেকে পাই, DA + DC > AC ……(ii)

(i) নং ও  (ii) নং সমীকরণ যোগ করে পাই,
AB + BC + DA + DC > AC + AC
∴ AB + BC + CD + DA > 2AC [প্রমাণিত]

4. ΔABC এর ভিতরে P যেকোনো একটি বিন্দু। প্রমাণ করি যে,
(i) AP + BP > AB
(ii) AB + BC + AC < 2 ( AP + BP + CP)

সমাধানঃ 

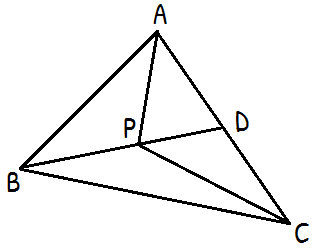
প্রদত্তঃ ∆ABC এর ভিতবে P যেকোনো একটি বিন্দু।

প্রামাণ্যঃ
(1) AP + BP > AB
(2) AB + BC + AC > 2(AP + BP + CP)

প্রমাণঃ
∆ABP থেকে পাই, AP + BP > AB ……(i) [(1) নং প্রমাণিত] 
∆BCP থেকে পাই, BP + CP > BC ……(ii)
ΔACP থেকে পাই, CP + AP > AC ……(iii)

{(i) + (ii)+ (iii)} করে পাই,
AP + BP + BP + CP + AP > AB + BC + AC
বা, 2(AP + BP + CP)>AB + BC + AC
∴ AB + BC + AC > 2(AP + BP + CP) [(2) নং প্রমাণিত]

5. প্রমাণ করি যে, ত্রিভুজের পরিসীমা ত্রিভুজটির মধ্যমা তিনটির দৈর্ঘ্যের সমষ্টির চেয়ে বড়ো।

সমাধানঃ 

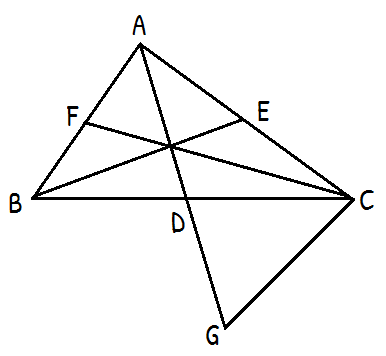
প্রদত্তঃ ABC ত্রিভুজের মধ্যমা তিনটি হল AD, BE  ও  CF

প্রামাণ্যঃ AB + BC + CA > AD + BE + CF

অঙ্কনঃ AD কে G পর্যন্ত এমনভাবে বর্ধিত করা হল যাতে AD = DG হয়। C, E যুক্ত করা হল।

প্রমাণঃ
ΔADB এবং ΔCDG এর মধ্যে,
BD = CD [\(\because \)  D, BC বাহুর মধ্যবিন্দু]
∠ADB = বিপ্রতীপ ∠CDG
AD=DG [অঙ্কনানুসারে]
∴ ΔADB ≅ ΔCDG [সর্বসমতার S-A-S শর্তানুসারে]

∴ AB = CG [সর্বসম ত্রিভুজের অনুরূপ বাহু]

ΔACG থেকে পাই,
AC + CG > AG
বা, AC + AB > AD + DG [\(\because \) AB = CG]
বা, AB + AC > AD + AD
∴ AB + AC > 2AD …….(i)

একইরকমভাবে, AB + BC > 2BE …….(ii)
এবং BC + AC > 2CF ……(iii)

(i) + (ii) + (iii) করে পাই,
AB + BC + AB + BC + BC + AC > 2AD + 2BE + 2CF
বা, 2(AB + BC + AC) > 2(AD + BE + CF)
∴ AB + BC + CA > AD + BE + CF [প্রমাণিত]

6. প্রমাণ করি যে, একটি চতুর্ভুজের কর্ণদ্বয়ের দৈর্ঘ্যের সমষ্টি চতুর্ভুজের যেকোনো দুটি বিপরীত বাহুর দৈর্ঘ্যের সমষ্টির চেয়ে বড়ো।

সমাধানঃ 

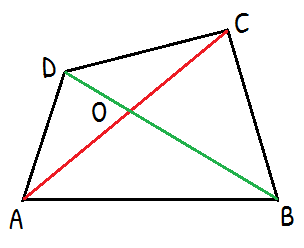
প্রদত্তঃ ABCD একটি চতুর্ভুজ। AC ও BD  কর্ণদুটি পরস্পরকে O বিন্দুতে ছেদ করে।

প্রামাণ্যঃ
(1) AC + BD > AD + BC এবং
(2) AC + BD > AB+DC

প্রমাণঃ
ΔAOD থেকে পাই,
OA + OD > AD ……(i)

ΔAOB থেকে পাই,
OA + OB > AB ……(ii)

ΔBOC থেকে পাই,
OB + OC > BC ……(iii)

ΔCOD থেকে পাই,
OC + OD > CD …….(iv)

(i) + (iii) করে পাই,
OA + OD+OB + OC > AD + BC
বা, (OA + OC) + (OD + OB) > AD + BC
∴ AC + BD > AD + BC [(1) নং প্রমাণিত]

(ii) + (iv) করে পাই,
OA + OB + OC+OD > AB + CD
বা, (OA + OC) + (OD + OB) > AB + CD
AC + BD > AB + CD  [(2) নং প্রমাণিত]

7. প্রমাণ করি যে, একটি চতুর্ভুজের কর্ণদ্বয়ের দৈর্ঘ্যের সমষ্টি চতুর্ভুজটির অর্ধ-পরিসীমার চেয়ে বড়ো।

সমাধানঃ 

প্রদত্তঃ ABCD একটি চতুর্ভুজ। AC ও BD  কর্ণদুটি পরস্পরকে O বিন্দুতে ছেদ করে।

প্রামাণ্যঃ AC + BD > \(\frac{1}{2} \)(AB + BC+ CD + AD)

প্রমাণঃ
ΔAOD থেকে পাই,
OA + OD > AD ……(i)

ΔAOB থেকে পাই,
OA + OB > AB ……(ii)

ΔBOC থেকে পাই,
OB + OC > BC  ……(iii)

ΔCOD থেকে পাই,
OC + OD > CD …….(iv)

(i) + (ii) + (iii) + (iv) করে পাই,
OA + OD + OA + OB + OB + OC + OC + OD > AB + BC+ CD + AD
বা, 2(OA + OB + OC + OD) > AB + BC+ CD + AD
বা, (OA + OC) + (OB + OD) > \(\frac{1}{2} \)(AB + BC + CD+ AD)
∴ AC + BD > \(\frac{1}{2} \)(AB + BC + CD + AD) [প্রমাণিত]

8. প্রমাণ করি যে, যেকোনো চতুর্ভুজের অন্তঃস্থ কোনো বিন্দু (কোনো কর্ণের উপর নয়) থেকে চতুভুজের শীর্ষবিন্দুগুলির সংযোজক সরলরেখাংশের দৈর্ঘ্যের সমষ্টি চতুভুজটির কর্ণদ্বয়ের দৈর্ঘ্যের সমষ্টির চেয়ে বড়ো। এবার দেখি যে চতুর্ভুজের ভিতর বিন্দুটির কোনো অবস্থানের জন্য চতুর্ভুজের শীর্ষবিন্দুগুলির সংযোজক সরলরেখাংশের দৈর্ঘ্যের সমষ্টি ক্ষুদ্রতম হবে।

সমাধানঃ 

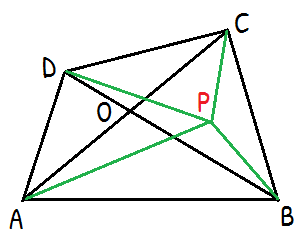
প্রদত্তঃ ধরি, ABCD একটি চতুর্ভুজ। চতুর্ভুজের ভিতর P যেকোনো একটি বিন্দু (কর্ণের উপর নয়)। AC ও BD কর্ণ পরস্পরকে O বিন্দুতে ছেদ করেছে।

প্রামাণ্যঃ
(1) AP + BP + CP + DP > AC + BD
(2) চতুর্ভুজের ভিতর বিন্দুটির কোনো অবস্থানের জন্য চতুর্ভুজের শীর্ষবিন্দুগুলির সংযোজক সরলরেখাংশের দৈর্ঘ্যের সমষ্টি ক্ষুদ্রতম হবে অর্থাৎ, চিত্রানুযায়ী আমাদেরকে প্রমাণ করতে হবে যে, P বিন্দুর অবস্থান যদি O বিন্দুতে হতো তাহলে শীর্ষবিন্দুগুলির দৈর্ঘ্যের সমষ্টি ক্ষুদ্রতম হবে।

প্রমাণঃ
∆APC থেকে পাই,
AP + CP > AC ……(i)

∆BPD থেকে পাই,
BP + DP > BD  ……(ii)

(i) + (ii) করে পাই,
AP + CP + BP + DP > AC + BD
বা, AP + CP + BP + DP > AO + CO + BO + DO
∴ AP + CP + BP + DP > AO + BO + CO + DO

অর্থাৎ, P বিন্দু থেকে শীর্ষবিন্দুগুলির দৈর্ঘ্যের সমষ্টি > O বিন্দু থেকে শীর্ষবিন্দুগুলির দৈর্ঘ্যের সমষ্টি

অর্থাৎ, P বিন্দুর অবস্থান যদি O বিন্দুতে হতো তাহলে শীর্ষবিন্দুগুলির দৈর্ঘ্যের সমষ্টি ক্ষুদ্রতম হবে। [প্রমাণিত]

Koshe Dekhi 20.1 Class 8

and visit Our website : learningscience.co.in 

আরও দেখুনঃ 

গণিত প্রকাশ দশম শ্রেণি – সম্পূর্ণ  সমাধান। 

গণিত প্রকাশ নবম শ্রেণি – সম্পূর্ণ  সমাধান।

গণিত প্রভা অষ্টম শ্রেণি – সম্পূর্ণ সমাধান। 

গণিত প্রভা সপ্তম শ্রেণি – সম্পূর্ণ সমাধান। 

গণিত প্রভা ষষ্ঠ শ্রেণি – সম্পূর্ণ সমাধান। 

জীবন বিজ্ঞান  (দশম শ্রেণী) (Life Science)

Thank You

Koshe dekhi 20.1 Class 8,Koshe dekhi 20.1 Class 8