Koshe Dekhi 6 class 9
Koshe Dekhi 6 class 9
1. প্রমাণ করি যে, একটি সামান্তরিকের কর্ণদ্বয়ের দৈর্ঘ্য সমান হলে সামান্তরিকটি একটি আয়তাকার চিত্র।
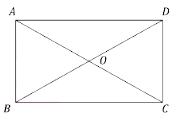
প্রদত্তঃ ধরি, ABCD একটি সামান্তরিক যার কর্ণদ্বয় AC ও BD এবং AC = BD
প্রমাণ করতে হবে যে, ABCD একটি আয়তক্ষেত্র।
প্রমাণঃ ΔABC এবং ΔBAD এর মধ্যে,
BC = AD [∵ সামান্তরিকের বিপরীত বাহু পরস্পর সমান]
AC = BD [প্রদত্ত]
এবং AB সাধারণ বাহু
ΔABC ≅ ΔBAD [সর্বসমতার S-S-S শর্তানুসারে]
∠ABC = ∠BAD [সর্বসম ত্রিভুজের অনুরূপ কোণ ] …….. (1)
আবার, ABCD সামান্তরিকের ∠ABC + ∠BAD = 180°
বা, ∠ABC + ∠ABC = 180° [(1) নং সমীকরণ অনুযায়ী]
বা, 2∠ABC = 180°
∴∠ABC = 90°
যেহেতু ABCD সামান্তরিকের ∠ABC = 90°
ABCD সামান্তরিকটি একটি আয়তক্ষেত্র। [প্রমাণিত]
2. প্রমাণ করি যে, একটি সামান্তরিকের কর্ণদ্বয়ের দৈর্ঘ্য সমান হলে এবং কর্ণদ্বয় পরস্পরকে লম্বভাবে ছেদ করলে সামান্তরিকটি একটি বর্গাকার চিত্র৷
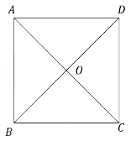
প্রদত্তঃ ধরি, ABCD সামান্তরিকের AC = BD এবং ∠AOB = ∠BOC = ∠COD = ∠AOD = 90°
প্রমাণ করতে হবে যে, ABCD একটি বর্গক্ষেত্র
প্রমাণঃ ΔABC ও ΔBAD এর –
AC = BD [দেওয়া আছে]
BC = AD [∵ সামান্তরিকের বিপরীত বাহু পরস্পর সমান]
AB সাধারণ বাহু
ΔABC ≅ ΔBAD [সর্বসমতার S-S-S শর্তানুসারে]
∠ABC = ∠BAD [সর্বসম ত্রিভুজের অনুরূপ কোণ] ……..(1)
আবার, ABCD সামান্তরিকের ∠ABC + ∠BAD = 180°
বা, ∠ABC + ∠ABC = 180° [(1) নং সমীকরণ অনুযায়ী]
বা, 2∠ABC = 180°
∴∠ABC = 90° ……..(2)
ΔAOB ও ΔAOD এর –
∠AOB = ∠AOD [প্রতিটি কোণ সমকোণ যা দেওয়া আছে]
BO = OD [∵ সামান্তরিকের কর্ণ পরস্পরকে সমদ্বিখন্ডিত করে]
AO সাধারণ বাহু
ΔAOB ≅ ΔAOD [সর্বসমতার S-S-S শর্তানুসারে]
AB = AD [সর্বসম ত্রিভুজের বিপরীত বাহু] ……..(3)
যেহেতু ABCD সামান্তরিকের ∠ABC = 90° এবং AB = AD [(2) ও (3) নং সিদ্ধান্ত অনুযায়ী]
ABCD সামান্তরিকটি বর্গক্ষেত্র। [প্রমাণিত]
3. প্রমাণ করি যে, একটি সামান্তরিকের কর্ণদ্বয় পরস্পরকে লম্বভাবে ছেদ করলে সামান্তরিকটি একটি রম্বস।
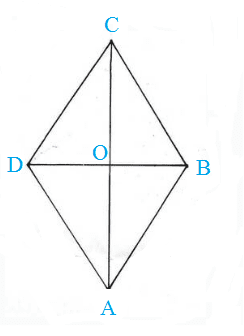 প্রদত্তঃ ABCD সামান্তরিকের AC ও BD কৰ্ণ দুটি পরস্পরকে O বিন্দুতে লম্বভাবে ছেদ করেছে।
প্রদত্তঃ ABCD সামান্তরিকের AC ও BD কৰ্ণ দুটি পরস্পরকে O বিন্দুতে লম্বভাবে ছেদ করেছে।
অর্থাৎ, ∠AOB = ∠BOC = ∠COD = ∠AOD = 90°
প্রমাণ করতে হবে যে, ABCD একটি রম্বস।
প্ৰমাণঃ ΔAOB ও ΔAOD এর মধ্যে
∠AOB = ∠AOD [প্রতিটি কোণ সমকোণ যা দেওয়া আছে]
BO = OD [∵ সামান্তরিকের কর্ণ পরস্পরকে সমদ্বিখন্ডিত করে]
AO সাধারণ বাহু
ΔAOB ≅ ΔAOD [সর্বসমতার S-S-S শর্তানুসারে]
AB = AD [সর্বসম ত্রিভুজের অনুরূপ বাহু]
∴ ABCD সামান্তরিকের AB = AD
অর্থাৎ, ABCD সামান্তরিকের একজোড়া সন্নিহিত বাহুর দৈর্ঘ্য সমান।
∴ ABCD সামান্তরিকটি রম্বস। [প্রমাণিত]
4. ABCD সামান্তরিকের AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করেছে। O বিন্দুগামী যেকোনাে সরলরেখা AB ও DC বাহুকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে। প্রমাণ করি যে OP = OQ
 প্রদত্তঃ ABCD সামান্তরিকের AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করেছে।O বিন্দুগামী PQ সরলরেখা AB ও DC বাহুকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে।
প্রদত্তঃ ABCD সামান্তরিকের AC ও BD কর্ণদ্বয় পরস্পরকে O বিন্দুতে ছেদ করেছে।O বিন্দুগামী PQ সরলরেখা AB ও DC বাহুকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে যে, OP = OQ
প্ৰমাণঃ ABCD সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বখন্ডিত করে।
∴AO = OC এবং BO = OD …….. (1)
ΔDOQ 3 ΔPOB এর-
∠DOQ = বিপ্রতীপ ∠POB
∠BPO = একান্তর ∠DQO [∵ AB || DC এবং PQ ছেদক]
BO = OD [(1) নং থেকে পাই]
∴ ΔDOQ ≅ ΔPOB [সর্বসমতার A-A-S শর্তানুসারে]
∴ OP = OQ [সর্বসম ত্রিভুজের অনুরূপ বাহু] [প্রমাণিত]
5. প্রমাণ করি যে, একটি সমদ্বিবাহু ট্রাপিজিয়ামের যেকোনাে সমান্তরাল বাহুসংলগ্ন দুটি কোণ পরস্পর সমান।
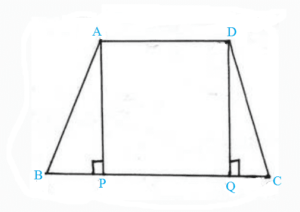 প্রদত্তঃ ধরি, ABCD একটি সমদ্বিবাহু ট্রাপিজিয়াম যার AB = DC.
প্রদত্তঃ ধরি, ABCD একটি সমদ্বিবাহু ট্রাপিজিয়াম যার AB = DC.
প্রমাণ করতে হবে যে, ∠ABC = ∠DCB
অঙ্কনঃ A ও D বিন্দু দিয়ে BC বাহুর উপর যথাক্রমে AP ও DQ লম্ব টানা হল।
প্ৰমাণঃ ΔABP ও ΔDCQ এর-
AB = DC
∠APB = ∠DQC [∵ AP ও DQ, BC বাহুর উপর লম্ব]
AP = DQ [∵ সমান্তরাল বাহুদ্বয়ের মধ্যে লম্ব দূরত্ব সর্বদা সমান]
ΔABP ≅ ΔDCQ [সর্বসমতার S-A-S শর্তানুসারে]
∠ABP = ∠DCQ [সর্বসম ত্রিভুজের অনুরূপ কোণ]
অর্থাৎ, ∠ABC = ∠DCB [প্রমাণিত]
6. ABCD বর্গাকার চিত্রে BC বাহুর উপর P যেকোনাে একটি বিন্দু৷ B বিন্দু থেকে AP-এর উপর অঙ্কিত লম্ব DC বাহুকে Q বিন্দুতে ছেদ করেছে৷ প্ৰমাণ করি যে, AP = BQ

প্ৰদত্তঃ ABCD বর্গাকার চিত্রে BC বাহুর উপর P যে কোনো একটি বিন্দু। B বিন্দু থেকে AP এর উপর অঙ্কিত লম্ব DC বাহুকে Q বিন্দুতে ছেদ করেছে। AP 3 BQ পরস্পরকে O বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে যে, AP = BQ
প্ৰমাণঃ ধরি, ∠BQC = x
ABCD একটি বর্গক্ষেত্র।
∴ ∠BCD = 90°
ΔBQC -এর ∠BQC + ∠BCQ + ∠QBC = 180°
বা, x + 90° + ∠QBC = 180° [∵ ∠BCD = ∠BCQ = 90°]
∴ ∠QBC = 90° − x ………. (1)
ΔBOP -এর ∠BOP = 90° [∵ AP ⊥ BQ]
আবার, ∠BOP + ∠OBP + ∠OPB = 180°
90° + 90° − x + ∠OPB = 180° [∵ ∠OBP = ∠QBC]
∠OPB = 180° – 180° + x
∴ ∠OPB = x
∴ ∠OPB = ∠BQC ……….. (2)
ΔAPB ও ΔBQC এর –
∠OPB = ∠BQC [(2) নং থেকে পাই]
∠ABP = ∠BCQ [∵ ABCD বর্গক্ষেত্রের ∠ABC = ∠BCD = 90°]
AB = BC [∵ ABCD একটি বর্গক্ষেত্র]
ΔAPB ≅ ΔBQC [সর্বসমতার A-A-S শর্তানুসারে]
AP = BQ [সর্বসম ত্রিভুজের অনুরূপ বাহু] [প্রমাণিত]
7. প্রমাণ করি যে, একটি চতুর্ভুজের দুটি বিপরীত কোণ পরস্পর সমান ও দুটি বিপরীত বাহু পরস্পর সমান্তরাল হলে, চতুর্ভুজটি একটি সামান্তরিক।

প্ৰদত্তঃ ABCD চতুর্ভুজের ∠ABC = ∠ADC এবং AB || DC
প্রমাণ করতে হবে যে, ABCD একটি সামান্তরিক।
অঙ্কনঃ BD কৰ্ণ অঙ্কন করলাম।
প্ৰমাণঃ ΔABD ও ΔBDC এর-
∠ABC = ∠ADC [দেওয়া আছে]
∠BCA =একান্তর ∠CAD [∵ AB || DC এবং AC ছেদক]
AC সাধারণ বাহু
ΔABD ≅ ΔBDC [সর্বসমতার A-A-S শর্তানুসারে]
∴ ∠ACD = ∠BAC [সর্বসম ত্রিভুজের অনুরূপ কোণ]
কিন্তু এরা একান্তর কোণ।
∴ AD || BC
ABCD চতুর্ভুজের AB || DC এবং AD || BC
∴ ABCD একটি সামান্তরিক। [প্রমাণিত]
8. ΔABC-এর BP ও CQ মধ্যমা দুটি যথাক্রমে R ও S বিন্দু পর্যন্ত এমনভাবে বর্ধিত করা হল যে, BP = PR এবং CQ = QS হয়। প্রমাণ করি যে, S, A, R বিন্দুতিনটি সমরেখ।
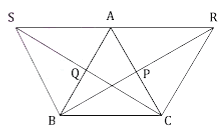
প্ৰদত্তঃ AABC এর BP 3 CQ দুটি মধ্যমা। BP = PR এবং CQ = QS
প্রমাণ করতে হবে যে, S, A, R বিন্দু তিনটি সমরেখ।
অঙ্কনঃ S, A; A, R; B, S এবং C, R যুক্ত করলাম।
প্রমাণঃ ASAQ এবং ABCQ এর –
CQ = QS [দেওয়া আছে]
∠AQS = বিপ্রতীপ ∠BOC
AQ = QB [∵ CQ, ΔABC এর মধ্যমা]
ΔSAQ ≅ ΔBCQ [S-A-S সর্বসমতার শর্তানুসারে]
সুতরাং, ∠QBC = ∠ASQ [সর্বসম ত্রিভুজের অনুরূপ কোণ]
∴ ∠ABC = ∠ASC, কিন্তু এরা একান্তর কোণ
∴ BC || SA
আবার, ΔARP এবং ΔBCP এর –
∴ BP = PR [দেওয়া আছে]
∠APR = বিপ্রতীপ ∠BPC
AP = PC [∵ BP, ΔABC এর মধ্যমা]
ΔARP ≅ ΔBCP [S-A-S সর্বসমতার শর্তানুসারে]
সুতরাং, ∠ARP = ∠CBP [সর্বসম ত্রিভুজের অনুরূপ কোণ]
∠ARB = ∠CBR, কিন্তু এরা একান্তর কোণ
∴ BC || AR
যেহেতু, BC || SA এবং BC || AR
∴ SA || AR
আবার যেহেতু, A বিন্দুটি SA ও AR দুটি সরলরেখাতেই আছে, সুতরাং, SA ও AR একই সরলরেখায় আছে।
∴ S, A, R বিন্দু তিনটি সমরেখ। [প্রমাণিত]
9. PQRS সামান্তরিকের SQ কর্ণ K ও L বিন্দুতে সমান তিনভাগে বিভক্ত হয়েছে। PK, SQ-কে M বিন্দুতে এবং RL, PQ কে N বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, PMRN একটি সামান্তরিক।

প্ৰদত্তঃ PQRS একটি সামান্তরিক। SQ কর্ণ K ও L বিন্দুতে সমান তিনভাগে বিভক্ত হয়েছে অর্থাৎ QL = LK = KS.
PK, SR কে M বিন্দুতে এবং RL, PQ কে N বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে যে, PMRN একটি সামান্তরিক
প্রমাণঃ ΔPQK এবং ΔRSL এর –
PQ = SR [∵ PQRS সামান্তরিকের বিপরীত বাহু]
QL + LK = LK + KS [∵ QL = LK = KS]
QK = LS
∠PQK = একান্তর ∠RSL [∵ PQ || SR এবং QS ভেদক]
ΔPQK ≅ ΔRSL [সর্বসমতার S-A-S শর্তানুসারে]
∠PKQ = ∠RLS [সর্বসম ত্রিভুজের অনুরূপ কোণ]
কিন্ত এরা একান্তর কোণ। ∴ PM || NR
ΔPSM এবং ΔRQN এর-
∠PMS =অনুরূপ ∠NRM [∵ PM || NR এবং SR ভেদক]
আবার, ∠RNQ = একান্তর ∠NRM [∵ PQ || SR এবং RN ভেদক]
∴ ∠RNQ = ∠PMS
∴ PQ = SR [∵ PQRS সামান্তরিকের বিপরীত বাহু]
∠RQN = ∠PSM [∵ PQRS সামান্তরিকের বিপরীত কোণ]
ΔPSM ≅ ΔRQN [সর্বসমতার S-A-S শর্তানুসারে]
∴ PM = NR [সর্বসম ত্রিভুজের অনুরূপ বাহু]
PMRN চতুর্ভুজের PM || NR এবং PM = NR
∴ PMRN একটি সামান্তরিক [প্রমাণিত]
10. ABCD ও AECF দুটি সামান্তরিকেরই AC একটি কর্ণ। B, E, D, F বিন্দুগুলি সমরেখ না হলে, প্রমাণ করি যে, BEDF একটি সামান্তরিক।

প্রদত্তঃ ABCD ও AECF দুটি সামান্তরিকেরই AC একটি কর্ণ।
প্রমাণ করতে হবে যে, BEDF একটি সামান্তরিক।
প্ৰমাণঃ ABCD সামান্তরিকের
∠CAD = একান্তর ∠ACB [∵ AD || BC এবং AC ছেদক] …. (1)
AECF সামান্তরিকের
∠CAF = একান্তর ∠ACE [∵ AD || BC এবং AC ছেদক] ….(2)
∠EAF = ∠ECF [AECF সামান্তরিকের বিপরীত কোণ] ….(3)
ΔAFD এবং ΔCEB এর-
∴ AD = BC [∵ ABCD সামান্তরিকের বিপরীত বাহু]
(2) – (1) করে পাই
∠CAD − ∠CAF = ∠ACB – ∠ACE
∠DAF = ∠BCE ……..(4)
AF = CE [∵ AECF সামান্তরিকের বিপরীত বাহু]
ΔAFD ≅ ΔCEB [সর্বসমতার S-A-S শর্তানুসারে]
সুতরাং, EB = DF [সর্বসম ত্রিভুজের অনুরূপ বাহু]
ΔAED এবং ΔCFB এর-
AD = BC [∵ ABCD সামান্তরিকের বিপরীত বাহু]
(3) + (4) করে পাই
∠EAF + ∠DAF = ∠BCE + ∠ECF
∠DAE = ∠BCF
AE = CF [∵ AECF সামান্তরিকের বিপরীত বাহু]
AAED = ACFB [সর্বসমতার S-A-S শর্তানুসারে]
সুতরাং, ED = BF [সর্বসম ত্রিভুজের অনুরূপ বাহু]
BEDF চতুর্ভুজের EB = DF এবং ED = BF
∴ BEDF একটি সামান্তরিক [প্রমাণিত]
11. ABCD একটি চতুর্ভুজ। ABCE ও BADF দুটি সামান্তরিক অঙ্কন করা হলাে। প্রমাণ করি যে, CD ও EF পরস্পরকে সমদ্বিখণ্ডিত করে।

প্ৰদত্তঃ ABCD একটি চতুর্ভুজ। ABCE ও BADF দুটি সামান্তরিক।
প্রমাণ করতে হবে যে, CD ও EF পরস্পরকে সমদ্বিখন্ডিত করে।
অঙ্কনঃ C, F ও E, D যুক্ত করা হল।
প্ৰমাণঃ যেহেতু, ABCE একটি সামান্তরিক
সুতরাং, AB = CE এবং AB || CE ….. (1)
যেহেতু, BADF একটি সামান্তরিক
সুতরাং, AB = DF এবং AB || DF …. (2)
(1) নং ও (2) নং থেকে পাই
CE = DF এবং CE || DF
CEDF চতুর্ভুজের CE = DF এবং CE || DF
∴ CEDF একটি সামান্তরিক
যেহেতু, সামান্তরিকের কর্ণদ্বয় পরস্পরকে সমদ্বিখন্ডিত করে।
সুতরাং, CEDF এর কর্ণদ্বয় CD ও EF পররস্পরকে সমদ্বিখন্ডিত করে।
∴ CD ও EF পররস্পরকে সমদ্বিখন্ডিত করে। [প্রমাণিত]
12. ABCD সামান্তরিকের AB = 2AD; প্রমাণ করি যে ∠BAD ও ∠ABC -এর সমদ্বিখণ্ডকদ্বয় DC বাহুর মধ্যবিন্দুতে সমকোণে মিলিত হয়।

প্ৰদত্তঃ ABCD সামান্তরিকের AB = 2AD
প্রমাণ করতে হবে যে,
(i) ∠AXB = 90°
(ii) X, DC বাহুর উপর অবস্থিত
(ii) DX = ½ DC
প্ৰমাণঃ ∠BAD এর সমদ্বিখন্ডক AX
∴ ∠DAX = ∠BAX = ½ ∠BAD … (1)
∠BAD এর সমদ্বিখন্ডক BX
∴∠CBX = ∠ABX = ½ ∠ABC … (2)
ABCD সামান্তরিকের AD || BC
∴ ∠BAD + ∠ABC = 180°
বা, ½ ∠BAD + ½ ∠ABC = ½ × 180°
∴ ∠BAX + ∠ABX = 90° [(1) ও (2) -এর সাহায্যে]
ABX ত্রিভুজের ∠BAX + ∠ABX + ∠AXB = 90°
বা, 90° + ∠AXB = 90°
∴ ∠AXB = 90° [(i) নং প্রমাণিত]
∠AXD = একান্তর ∠BAX [∵ AB || DC এবং AX ভেদক]….(3)
∠BXC = একান্তর ∠ABX [∵ AB || DC এবং BX ভেদক] …..(4)
এখন ∠AXD + ∠AXB + ∠BXC
= ∠BAX + 90° + ∠ABX [(3) নং ও (4) নং থেকে পাই]
= 90° + 90°
= 180°
সুতরাং, X বিন্দুটি DC সরলরেখার উপর অবস্থিত। [(ii) নং প্রমাণিত]
(3) নং থেকে পাই, ∠AXD = ∠BAX
আবার, ∠DAX = ∠BAX [∵ ∠BAD এর সমদ্বিখন্ডক AX]
∴ ∠AXD = ∠DAX
ΔABC এর ∠AXD = ∠DAX
∴ DX = AD
∴ DX = ½ AB = ½ DC [∵ ABCD সামান্তরিকের AB = DC] [(iii) নং প্রমাণিত]
13. ABCD সামান্তরিকের AB ও AD বাহুর উপর যথাক্রমে ABPQ ও ADRS বর্গাকার চিত্র অঙ্কন করা হলাে যারা সামান্তরিকটির বাইরে অবস্থিত। প্রমাণ করি যে, PRC ত্রিভুজটি সমদ্বিবাহু।

প্ৰদত্তঃ ABCD সামান্তরিকের AB ও AD বাহুর উপর যথাক্রমে ABPQ ও ADRS বর্গাকার চিত্র অঙ্কন করা হল যারা সামান্তরিকের বাইরে অবস্থিত। প্রমাণ করতে হবে যে, PRC ত্রিভুজটি সমদ্বিবাহু।
প্ৰমাণঃ ABCD একটি সামান্তরিক
∴ AB = CD, BC = AD এবং ∠ABC = ∠ADC
AB = PB [∵ ABPQ একটি বর্গক্ষেত্র]
∴ PB = CD [∵ AB = CD] …. (1)
AD = DR [∵ ABPQ একটি বর্গক্ষেত্র]
∴ BC = DR [∵ BC = AD] …. (2)
যেহেতু, ABPQ একটি বর্গক্ষেত্র
∴ ∠ABP = 90°
এবং ADRS একটি বর্গক্ষেত্র
∴ ∠ADR = 90°
∠ABP + ∠ABC
= ∠ADR + ∠ADC [∵∠ABC = ∠ADC]
∴ ∠CBP = ∠CDR …. (3)
ΔCBP এবং ΔCDR এর-
PB = CD [(1) নং থেকে পাই]
∠CBP = ∠CDR [(3) নং থেকে পাই]
BC = DR [(2) নং থেকে পাই]
∴ ΔCBP ≅ ΔCDR [সর্বসমতার S-A-S শর্তানুসারে]
সুতরাং, CP = CR [সর্বসম ত্রিভুজের অনুরূপ বাহু]
ΔPRC এর CP = CR
∴ PRC একটি সমদ্বিবাহু ত্রিভুজ। [প্রমাণিত]
14. ABCD সামান্তরিকের ∠BAD স্থূলকোণ; AB ও AD বাহুর উপর দুটি সমবাহু ত্রিভুজ ABP ও ADQ অঙ্কন করা হলাে যারা সামান্তরিকের বাইরে অবস্থিত। প্রমাণ করি যে, CPQ একটি সমবাহু ত্রিভুজ।

প্রদত্তঃ ABCD সামান্তরিকের LBAD স্থূলকোণ; AB ও CD বাহুর উপর দুটি সমবাহু ত্রিভুজ অঙ্কন ABP ও ADQ অঙ্কন করা হল যারা সামান্তরিকের বাইরে অবস্থিত।
প্রমাণ করতে হবে যে, CPQ একটি সমবাহু ত্রিভুজ।
প্ৰমাণঃ যেহেতু, ABP একটি সমবাহু ত্রিভুজ
∴ AB = PB = AP
∴ PB = CD [∵ ABCD সামান্তরিকের AB = CD] ….(1)
যেহেতু, ADQ একটি সমবাহু ত্রিভুজ
∴ AD = DQ
∴ BC = DQ [∵ ABCD সামান্তরিকের BC = AD] ….(2)
যেহেতু, ABP ও ADQ উভয়েই সমবাহু ত্রিভুজ
∴ ∠ABP = 60° এবং ∠ADQ = 60°
∠ABP + ∠ABC = ∠ADQ + ∠ADC [∵ ABCD সামান্তরিকের ∠ABC = ∠ADC]
∴∠CBP = ∠CDQ ….. (3)
ΔCBP এবং ΔCDQ এর-
PB = CD [(1) নং থেকে পাই ]
∠CBP = ∠CDQ [(3) নং থেকে পাই]
BC = DQ [(2) নং থেকে পাই]
∴ ΔCBP ≅ ΔCDQ [সর্বসমতার S-A-S শর্তানুসারে]
∴ CP = CQ [সর্বসম ত্রিভুজের অনুরূপ বাহু] …. (4)
এখন, ∠PAQ + ∠PAB + ∠BAD + ∠DAQ = 360°
বা, ∠PAQ + 60° + ∠BAD + 60° = 360°
বা, ∠PAQ + 120° + 180° − ∠ADC = 360° [∠BAD + ∠ADC = 180°]
বা, ∠PAQ = 360° − 300° + ∠ADC
বা, ∠PAQ = 60° + ∠ADC
বা, ∠PAQ = ∠ADQ + ∠ADC
∴ ∠PAQ = ∠CDQ ….. (5)
ΔPAQ এবং ΔCDQ এর-
AQ = AD [∵ ADQ একটি সমবাহু ত্রিভুজ]
∠PAQ = ∠CDQ [(5) নং থেকে পাই]
PA = DC [PA = PB এবং (2) নং থেকে পাই]
ΔPAQ ≅ ΔCDQ [সর্বসমতার S-A-S শর্তানুসারে]
PQ = CQ [সর্বসম ত্রিভুজের অনুরূপ বাহু] …. (6)
(4) নং ও (6) নং থেকে পাই, CP = CQ = PQ
∴ CPQ একটি সমবাহু ত্রিভুজ [প্রমাণিত ]
15. OP, OQ ও OR তিনটি সরলরেখাংশ। OPAQ, OQBR এবং ORCP সামান্তরিক তিনটি অঙ্কন করা হলাে। প্রমাণ করি যে, AR , BP ও CQ পরস্পরকে সমদ্বিখণ্ডিত করে।

প্ৰদত্তঃ OPAQ, OQBR এবং ORCP তিনটি সামান্তরিক। AR, BP ও CQ পরস্পরকে X বিন্দুতে ছেদ করেছে।
প্রমাণ করতে হবে যে, AX = XR, BX = XP এবং CX = XQ
প্ৰমাণঃ OQBR সামান্তরিকের OR = QB এবং OR || QB ….(1)
ORCP সামান্তরিকের OR = PC এবং OR || PC ….(2)
(1) নং ও (2) নং থেকে পাই
QB = PC এবং QB || PC ….(3)
ΔXBQ এবং ΔXPC এর মধ্যে ∠BXQ = বিপ্রতীপ ∠CXP
∠XBQ = একান্তর ∠XPC [∵ QB||PC এবং PB ছেদক]
QB = PC [(4) নং থেকে পাই]
∴ ΔXBQ ≅ ΔXPC [সর্বসমতার A A S শর্তানুসারে]
BX = XP [সর্বসম ত্রিভুজের অনুরূপ বাহু]
এবং CX = XQ [সর্বসম ত্রিভুজের অনুরূপ বাহু] …(4)
OQBR সামান্তরিকের OQ = RB এবং OQ || RB …(5)
OPAQ সামান্তরিকের OQ = PA এবং OQ || PA …(6)
(5) নং ও (6) নং থেকে পাই
RB = PA এবং RB || PA ….(7)
ΔXBQ এবং ΔXPC এর মধ্যে ∠BXR = বিপ্রতীপ ∠AXP
∠XRB = একান্তর ∠XAP [∵ RB || PA এবং AR ছেদক]
RB = PA [(7) নং থেকে পাই]
ΔXBQ ≅ ΔXPC [সর্বসমতার A-A-S শর্তানুসারে]
∴ AX = XR [সর্বসম ত্রিভুজের অনুরূপ বাহু] ….(8)
(4) নং ও (8) নং থেকে পাই
AX = XR, BX = XP এবং CX = XQ [প্রমাণিত]
16. বহু বিকল্পীয় প্রশ্ন: (M.C.Q.):
(i) ABCD সামান্তরিকের ∠BAD = 75° এবং ∠CBD = 60° হলে ∠BDC-এর পরিমাপ
(a) 60°
(b) 75°
(c) 45°
(d) 50°
উত্তরঃ (c) 45°

ABCD সামান্তরিকের ∠BAD = ∠BCD
∴ ∠BCD = 75°
ΔBCD থেকে পাই,
∠BDC = 180° – ∠BCD – ∠CBD
= 180° − 75° − 60°
= 45°
উত্তরঃ (c) 45°
16. বহু বিকল্পীয় প্রশ্ন: (M.C.Q.):
(ii) নিম্নলিখিত জ্যামিতিক চিত্রগুলির কোনটির কর্ণদ্বয়ের দৈর্ঘ্য সমান তা লিখি।
(a) সামান্তরিক
(b) রম্বস
(c) ট্রাপিজিয়াম
(d) আয়তাকার চিত্র
উত্তরঃ (d) আয়তাকার চিত্র
16. বহু বিকল্পীয় প্রশ্ন: (M.C.Q.):
(iii) ABCD সামান্তরিকের ∠BAD = ∠ABC হলে ABCD সামান্তরিকটি
(a) রম্বস
(b) ট্রাপিজিয়াম
(c) আয়তাকার চিত্র
(d) কোনােটিই নয়
উত্তরঃ (c) আয়তাকার চিত্র
 ABCD সামান্তরিকের ∠BAD = ∠ABC
ABCD সামান্তরিকের ∠BAD = ∠ABC
আবার, ABCD সামান্তরিকের ক্ষেত্রে
∠BAD + ∠ABC = 180°
বা, 2∠BAD = 180° [∵∠BAD = ∠ABC]
∴ ∠BAD = 90°
∵ ABCD সামান্তরিকের ∠BAD = 90°
∴ ABCD সামান্তরিকটি একটি আয়তক্ষেত্র।
উত্তরঃ (c) আয়তাকার চিত্র
16. বহু বিকল্পীয় প্রশ্ন: (M.C.Q.):
(iv) ABCD সামান্তরিকের BD কর্ণের মধ্যবিন্দু M; BM, ∠ABC-কে সমদ্বিখণ্ডিত করলে ∠AMB এর পরিমাপ
(a) 45°
(b) 60°
(c) 90°
(d) 75°
উত্তরঃ (c) 90°

BM, ∠ABC এর সমদ্বিখন্ডক
∴ ∠ABD = ∠CBD
আবার, ∠CDB = একান্তর ∠ABD
∴ ∠CDB = ∠CBD [∵ ABCD সমন্তরিকের AB || CD এবং BD ভেদক]
ΔBCD এর ∠CDB = ∠CBD
∴ BC = CD
ABCD সামান্তরিকের BC = CD
∴ ABCD সামান্তরিকটি একটি রম্বস ।
যেহেতু, রম্বসের কর্ণদ্বয় পরস্পরকে সমকোণে সমদ্বিখন্ডিত করে
∴ ∠AMB = 90°
উত্তরঃ (c) 90°
16. বহু বিকল্পীয় প্রশ্ন: (M.C.Q.):
(v) ABCD রম্বসের ∠ACB = 40° হলে ∠ADB -এর পরিমাপ
(a) 50°
(b) 110°
(c) 90°
(d) 120°
উত্তরঃ (a) 50°

∠CAD = একান্তর ∠ACB = 40° [∵ AD || BC এবং AC ছেদক]
∴ ∠MAD = 40°
ΔAMD এর ∠ADM
= 180° – ∠MAD – ∠AMD
= 180° − 40° − 90°
= 50°
∴ ∠ADM = 50°
উত্তরঃ (a) 50°
17. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন :
(i) ABCD সামান্তরিকের ∠A : ∠B = 3 : 2 হলে সামান্তরিকটির কোণগুলির পরিমাপ লিখি।
সমাধানঃ

ধরি, ∠A = 3x° এবং ∠B = 2x°
যেহেতু সামান্তরিকের পাশাপাশি দুটি অন্তঃস্থ কোণের সমষ্টি 180°
∴ 3x + 2x = 180
বা, 5x = 180
∴ x = 36
∴ ∠A = 3 × 36° = 108°
এবং ∠B = 2 × 36° = 72°
ABCD সামান্তরিকের বিপরীত কোণগুলি পরস্পর সমান
∴ ∠A = ∠C = 108° এবং ∠B = ∠D = 72°
উত্তরঃ ABCD সামান্তরিকের ∠A = 108°, ∠B = 72°, ∠C = 108° এবং ∠D = 72°
17. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন :
(ii) ABCD সামান্তরিকের ∠A ও ∠B-এর সমদ্বিখণ্ডদ্বয় CD বাহুর উপর E বিন্দুতে মিলিত হয়। BC বাহুর দৈর্ঘ্য 2 সেমি. হলে, AB বাহুর দৈর্ঘ্য কত তা লিখি।
সমাধানঃ

ABCD সামান্তরিকের ∠A ও ∠B এর সমদ্বিখন্ডকদ্বয় CD বাহুর উপর E বিন্দুতে মিলিত হয় এবং BC = 2 সেমি.।
∠ABE = ∠CBE [∵ BE, ∠ABC এর সমদ্বিখন্ডক]
∠ABE = একান্তর ∠BEC [∵ AB || CD এবং BE ছেদক]
∴ ∠CBE = ∠BEC
∴ CE = BC
একইরকমভাবে, AD = DE
আবার, BC = AD [∵ সামান্তরিকের বিপরীত বাহু পরস্পর সমান]
∴ DE = BC = 2 সেমি.
∴ DC = DE + CE
= (2 + 2) সেমি. = 4 সেমি.
আবার, AB = DC [∵ সামান্তরিকের বিপরীত বাহু পরস্পর সমান]
∴ AB = 4 সেমি.
উত্তরঃ AB বাহুর দৈর্ঘ্য 4 সেমি.
17. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন :
(iii) ABCD বর্গাকার চিত্রের ভিতর সমবাহু ত্রিভুজ AOB অবস্থিত৷ ∠COD -এর পরিমাপ লিখি।
সমাধানঃ

ABCD একটি বর্গক্ষেত্র
∴ AB = BC = CD = DA ….(1)
AOB একটি সমবাহু ত্রিভুজ
∴ AB = BO = AO …..(2)
এবং ∠A0B = ∠OBA = ∠0AB = 60°
(1) নং ও (2) নং থেকে পাই
AD = AO এবং BC = BO
AOD ত্রিভুজের AD = AO
∴ ∠AOD = ∠ADO
আবার, AOD ত্রিভুজ থেকে পাই,
∠AOD + ∠ADO + ∠OAD = 180°
বা, ∠AOD + ∠AOD + (∠BAD − ∠OAB)
বা, 2∠AOD + (90° – 60°) = 180°
বা, 2∠AOD = 180° – 30°
বা, 2∠AOD = 150°
∴ ∠AOD = 75°
একইরকমভাবে, ∠BOC = 75°
এখন, ∠AOB + ∠BOC + ∠COD + ∠AOD = 360°
বা, 60° + 75° + ∠COD + 75° = 360°
বা, ∠COD = 360° – 60° – 75° – 75°
∴ ∠COD = 150°
উত্তরঃ ∠COD = 150°
17. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন :
(iv) ABCD বর্গাকার চিত্রের AD বাহুর উপর M একটি বিন্দু যাতে ∠CMD = 30° হয়। কর্ণ BD, CM-কে P বিন্দুতে ছেদ করলে ∠DPC-এর পরিমাপ কত তা লিখি।
সমাধানঃ

ABCD একটি বর্গক্ষেত্র
∴ ∠BCD = ∠ADC
∠BCM = একান্তর ∠CMD [∵ AD || BC এবং CM ছেদক]
∴ ∠BCM = 30°
∠DCM = 90° – ∠BCM
= 90° – 30°
∴ ∠DCM = ∠DCP = 60°
আবার, ∠BDC = ∠ADC = 2 × 90° = 45°
∴ ∠PDC = 45°
DPC ত্রিভুজের
∠DPC = 180° – ∠PDC – ∠PCD
= 180° – 45° — 60°
= 75°
উত্তরঃ ∠DPC = 75°
17. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন :
(v) ABCD রম্বসের AB বাহুর দৈর্ঘ্য 4 সেমি. এবং ∠BCD = 60° হলে কর্ণ BD -এর দৈর্ঘ্য কত তা লিখি।
সমাধানঃ

BCD ত্রিভুজের BC = CD
∴ ∠CBD = ∠BDC
যেহেতু, ত্রিভুজের তিনটি কোণের সমষ্টি 180°
∴ ∠CBD + ∠BDC + ∠BCD = 180°
বা, ∠CBD +∠CBD + 60° = 180°
বা, 2∠CBD = 180° – 60°
বা, 2∠CBD = 120°
∴ ∠CBD = 60°
BCD ত্রিভুজের ∠CBD = ∠BDC = ∠BCD = 60°
∴ BCD ত্রিভুজটি একটি সমবাহু ত্রিভুজ
∴ BC = CD = BD
আবার, ABCD রম্বসের AB = BC = CD
∴ BD = AB = 4 সেমি.
উত্তরঃ কর্ণ BD এর দৈর্ঘ্য 4 সেমি.
koshe dekhi 6 class 9
Support Me
If you like my work then you can Support me by contributing a small amount which will help me a lot to grow my Website. It’s a request to all of you. You can donate me through phone pay / Paytm/ Gpay on this number 7980608289 or by the link below :
and visit Our website : learningscience.co.in
গণিত প্রকাশ (দশম শ্রেণী) সম্পূর্ণ সমাধান
গণিত প্রকাশ (নবম শ্রেণী) সম্পূর্ণ সমাধান
গণিত প্রভা (ষষ্ঠ শ্রেণী) সম্পূর্ণ সমাধান
জীবন বিজ্ঞান (দশম শ্রেণী) (Life Science)