Koshe Dekhi 7.2 Class 10
Koshe Dekhi 7.2 Class 10
Q1. পাশের ছবিতে ∠DBA = 40°, ∠BAC = 60° এবং ∠CAD = 20°; ∠DCA ও ∠BAC -এর মান নির্ণয় করি। ∠BAD ও ∠DCB -এর মানের সমষ্টি কত হবে হিসাব করে দেখি।
সমাধান :
|
koshe dekhi 7.2 class 10
Q2. পাশের চিত্রে AOB বৃত্তের ব্যাস এবং O বৃত্তের কেন্দ্র। OC ব্যাসার্ধ AB এর উপর লম্ব। যদি উপচাপ CB -এর উপর কোনো বিন্দু P হয়, তবে ∠BAC ও ∠APC -এর মান হিসাব করে লিখি।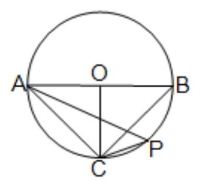
সমাধান :
|
koshe dekhi 7.2 class 10
| Q3. ABC ত্রিভুজের O লম্ববিন্দু এবং BC -এর উপর অঙ্কিত লম্ব AD -কে বর্ধিত করলে ΔABC -এর পরিবৃত্তকে G বিন্দুতে ছেদ করে। প্রমাণ করি যে, OD = DG.
সমাধান :
ΔABC -এর তিনটি লম্ব সমদ্বিখন্ডক AD, BE এবং CF পরস্পরকে O বিন্দুতে ছেদ করেছে। AD কে বর্ধিত করলে তা পরিবৃত্তকে G বিন্দুতে ছেদ করে। প্রমান করতে হবে যে, OD = DG অঙ্কনঃ G, C এবং G, B যুক্ত করা হল। প্রমানঃ AB উপচাপের ওপর অবস্থিত বৃত্তস্থ কোণ ∠ACB ও ∠AGB ∠ACB = ∠AGB (একই বৃত্তচাপ দ্বারা গঠিত সকল বৃত্তস্থ কোণের মান সমান) অর্থাৎ, ∠ECD = ∠BGD
চতুর্ভূজ EODC -এর ∠OEC এবং ∠ODC উভয়েই সমকোণ। ∴ ∠ECD + ∠EOD = 180° —– (i)
আবার, BE সরলরেখার ওপর O বিন্দুতে OD দন্ডায়মান। ∴ ∠BOD + ∠EOD = 180° —– (ii)
(i) এবং (ii) নং সমীকরন দুটি তুলনা করে পাই, ∠ECD + ∠EOD = ∠BOD + ∠EOD অর্থাৎ, ∠ECD = ∠BOD আবার, ∠ECD = ∠BGD ∴ ∠BOD = ∠BGD
এখন ΔBOD এবং ΔBGD এর মধ্যে ∠BOD = ∠BGD [প্রমানিত] ∠BDO = ∠BDG [উভয়েই সমকোণ] এবং BD সাধারন বাহু ∴ ΔBOD ≅ ΔBGD [A-A-S সর্বসমতা আনুসারে] ∴ OD = DG [সর্বসম ত্রিভুজের অনুরূপবাহু] (প্রমানিত) |
Support Me
If you like my work then you can Support me by contributing a small amount which will help me a lot to grow my channel. It’s a request to all of you. You can donate me through phone pay / Paytm/ Gpay on this number 7980608289 or by the link below :
koshe dekhi 7.2 class 10
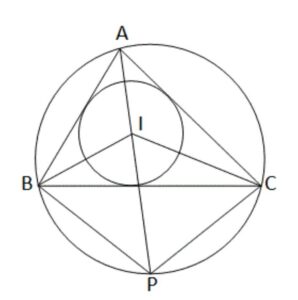
| Q4. ΔABC -এর অন্তবৃত্তের কেন্দ্র I; বর্ধিত AI ত্রিভুজের পরিবৃত্তকে P বিন্দুতে ছেদ করে। প্রমাণ করি যে, PB = PC = PI.
সমাধান :
ΔABC এর অন্তঃকেন্দ্র I এবং বর্ধিত AI, ΔABC এর পরিবৃত্তকে P বিন্দুতে ছেদ করেছে। প্রমান করতে হবে যে, PB = PC = PI অঙ্কনঃ P, B; P, C; B, I এবং C, I যুক্ত করা হল। প্রমানঃ ∵ I, ΔABC -এর অন্তঃকেন্দ্র ∴ AI, BI ও CI হল যথাক্রমে ΔABC -এর ∠BAC, ∠ABC ও ∠ACB কোণগুলির সমদ্বিখন্ডক। আবার, ∵ ΔABC এর পরিবৃত্তের PC বৃত্তচাপ দ্বারা গঠিত দুটি বৃত্তস্থ কোণ ∠PBC এবং ∠PAC ∴ ∠PBC = ∠PAC [একই বৃত্তচাপ দ্বারা গঠিত সকল বৃত্তস্থ কোণের মান সমান] আবার ∠PAC = ∴ ∠PAC = ∠PBC = এখন ∠IBP = ∠IBC + ∠PBC ∠IBP =
আবার, যেহেতু, ΔABI এর বহিঃস্থ কোণ ∠BIP ও অন্তঃস্থ বিপরীত কোণ দুটি হল ∠IBA ও ∠IAB ∴ ∠BIP = ∠IBA + ∠IAB ∠BIP =
(i) এবং (ii) নং সমীকরন দুটি তুলনা করে পাই, ∠IBP = ∠BIP এখন যা পেলাম, তা হল ΔIBP -এর ∠IBP = ∠BIP ∴ PB = PI [কোনও ত্রিভুজের সমান কোণগুলির বিপরীত বাহুগুলি সমান হয়] অনুরূপভাবে, ΔIPC থেকে প্রমান করা যায় যে, PC = PI ∴ PB = PC = PI (প্রমানিত) |
koshe dekhi 7.2 class 10
| Q5. তিমির দুটি বৃত্ত এঁকেছে যারা পরস্পরকে P ও Q বিন্দুতে ছেদ করেছে। P বিন্দু দিয়ে দুটি সরলরেখা টানলাম যারা একটি বৃত্তকে A, B বিন্দুতে এবং অপর বৃত্তকে যথাক্রমে C, D বিন্দুতে ছেদ করল। প্রমাণ করি যে, ∠AQC = ∠BQD .
সমাধান :
ধরি, M এবং N কেন্দ্রীয় দুটি বৃত্ত পরস্পরকে P এবং Q বিন্দুতে ছেদ করেছে। P বিন্দুতে দুটি সরলরেখা M কেন্দ্রীয় বৃত্তকে যথাক্রমে A, B এবং N কেন্দ্রীয় বৃত্তকে C, D বিন্দুতে ছেদ করেছে। প্রমান করতে হবে যে, ∠AQC = ∠BQD প্রমানঃ ∵ M কেন্দ্রীয় বৃত্তের ক্ষেত্রে, ∠PAQ ও ∠PBQ হল একই বৃত্তাংশস্থ কোণ সমূহ। ∠PAQ = ∠PBQ [∵ একইবৃত্তাংশস্থ সকল কোণের মান সমান] আবার, ∵ N কেন্দ্রীয় বৃত্তের ক্ষেত্রে, ∠PCQ ও ∠PDQ হল একই বৃত্তাংশস্থ কোণ সমূহ। ∠PCQ = ∠PDQ [∵ একইবৃত্তাংশস্থ সকল কোণের মান সমান] এখন, ∠PAQ + ∠PCQ = ∠PBQ + ∠PDQ —– (i) ΔACQ এর ক্ষেত্রে, ∠AQC = 180° – (∠PAQ + ∠PCQ) [ত্রিভুজের তিনটি কোণের সমষ্টি 180°] বা, ∠AQC = 180° – (∠PBQ + ∠PDQ) [ (i) নং সমীকরণ ব্যবহার করে পেলাম] ∴ ∠AQC = ∠BQD [∵ ΔBQD এর ক্ষেত্রে, ∠BQD = 180° – (∠PBQ + ∠PDQ) ] (প্রমানিত) |
koshe dekhi 7.2 class 10
| Q6. একটি বৃত্তের AB ও CD জ্যা দুটি পরস্পর লম্ব | AB ও CD জ্যা দুটির ছেদবিন্দু P থেকে AD এর উপর অঙ্কিত লম্বকে বর্ধিত করলে সেটি BC -কে E বিন্দুতে ছেদ করে, তবে প্রমাণ করি যে, E, BC -এর মধ্যবিন্দু।
সমাধান :
AB এবং CD জ্যা দুটি পরস্পরকে P বিন্দুতে ছেদ করেছে। P বিন্দু দিয়ে AD এর ওপর PF হলো লম্ব। FP কে বর্ধিত করলে তা BC কে E বিন্দুতে ছেদ করে। প্রমান করতে হবে যে, E, BC এর মধ্যবিন্দু। প্রমানঃ যেহেতু সমকোণী ΔFPD -এর PF ⊥ FD ∴ ∠FPD = 90° – ∠FDP ——(i)
আবার, যেহেতু সমকোণী ΔAPD -এর AP ⊥ PD ∴ ∠PAD = 90° – ∠ADP অর্থাৎ, ∠PAD = 90° – ∠FDP [∠ADP ও ∠FDP একই কোণ] ∴ ∠FPD = ∠PAD —– (ii) [(i) ও (ii) নং সমীকরণ দুটি তুলনা করে পেলাম]
অনুরূপভাবে, ∠APF = ∠FDP —– (iii)
AC উপচাপ দ্বারা গঠিত দুটি বৃত্তস্থ কোণ হলো ∠ADC ও ∠ABC ∴ ∠ADC = ∠ABC
আবার, DB উপচাপ দ্বারা গঠিত দুটি বৃত্তস্থ কোণ হলো ∠D AB ও ∠BCD ∠DAB = ∠BCD অর্থাৎ, ∠PAD = ∠PCE —– (iv) [∠DAB ও ∠PAD একই কোণ এবং ∠BCD ও ∠PCE একই কোণ]
এখন, (ii) ও (iv) নং সমীকরণ দুটি তুলনা করে পাই- ∠FPD = ∠PCE —— (v)
এখন, ΔCPE -এর ∠PCE = ∠PAD [(iv) নং সমীকরণ অনুসারে] ∠CPE = ∠FPD [বিপ্রতীপ কোণ] ∴ ∠CPE = ∠PCE [(v) নং সমীকরণ অনুসারে] সুতরাং, CE = PE —– (vi) [ত্রিভুজের যে দুটি বাহুর দৈর্ঘ্য সমান তাদের বিপরীত কোনগুলি সমান হয়]
অনুরূপভাবে, ΔPEB থেকে প্রমাণ করা যায় যে, BE = PE —— (vii)
এখন, (vi) এবং (vii) সমীকরন দুটি তুলনা করে পাই, CE = BE. অর্থাৎ, E, BC এর মধ্যবিন্দু। (প্রমানিত) |
koshe dekhi 7.2 class 10
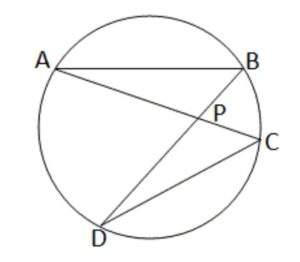
| Q7. যদি ABCD বৃত্তস্থ চতুর্ভুজের AB = DC হয়, তবে প্রমাণ করি যে, AC = BD হবে।
সমাধান :
বৃত্তের AB এবং DC দুটি সমান দৈর্ঘ্যের জ্যা। প্রমান করতে হবে যে, AC = BD অঙ্কনঃ A, C এবং B, D যুক্ত করা হল। AC এবং BD পরস্পরকে P বিন্দুতে ছেদ করল। প্রমানঃ যেহেতু, BC উপচাপ দ্বারা গঠিত দুটি বৃত্তস্থ কোণ হলো ∠BAC এবং ∠BDC ∴ ∠BAC = ∠BDC [একই বৃত্তচাপ দ্বারা গঠিত সকল বৃত্তস্থ কোণের মান সমান] অর্থাৎ, ∠BAP = ∠PDC —– (i)
এখন, যেহেতু ΔAPB এবং ΔDPC -এর AB = DC [স্বীকারানুসারে] ∠APB = ∠DPC [বিপ্রতীপ কোণ সমূহ] ∠BAP = ∠PDC [(i) সমীকরণ অনুসারে] ΔAPB ≅ ΔDPC [S-A-A সর্বসমতা অনুসারে] AP = DP এবং PB = PC [সর্বসম ত্রিভুজের অনুরূপ বাহু সমূহ]
এখন, AP + PC = DP + PB অর্থাৎ, AC = BD (প্রমানিত) |
koshe dekhi 7.2 class 10
| Q8. O কেন্দ্রীয় বৃত্তে OA ব্যাসার্ধ এবং AQ একটি জ্যা। বৃত্তের উপর C একটি বিন্দু। O, A, C বিন্দুগামী বৃত্ত AQ জ্যা-কে P বিন্দুতে ছেদ করে।
সমাধান :
O কেন্দ্রীয় বৃত্তের OA ব্যাসার্ধ এবং AQ হলো একটি জ্যা। বৃত্তের ওপর C যেকোনাে একটি বিন্দু। O, A, C বিন্দুগামী বৃত্ত AQ জ্যা কে P বিন্দুতে ছেদ করেছে। প্রমান করতে হবে যে, CP = PQ অঙ্কনঃ O, Q ; O, C এবং C, Q যুক্ত করা হল। প্রমানঃ ΔOAQ -এর OA = OQ [একই বৃত্তের ব্যাসার্ধ] ∴ ∠OAQ = ∠OQA [ত্রিভুজের যে দুটি বাহুর দৈর্ঘ্য সমান তাদের বিপরীত কোনগুলি সমান হয়] অর্থাৎ, ∠PAO = ∠OQP —–(i)
আবার, O, A, C বিন্দুগামী বৃত্তের OP উপচাপ দ্বারা গঠিত দুটি বৃত্তস্থ কোণ ∠OCP এবং ∠PAO ∴ ∠OCP = ∠PAO —– (ii) [একই বৃত্তচাপ দ্বারা গঠিত সকল বৃত্তস্থ কোণের মান সমান]
এখন, (i) ও (ii) নং সমীকরণ দুটি তুলনা করে পাই, ∠OCP = ∠OQP ——(iii)
এখন, ΔOCQ -এর OC = OQ [একই বৃত্তের ব্যাসার্ধ] ∴ ∠OCQ = ∠OQC [ত্রিভুজের যে দুটি বাহুর দৈর্ঘ্য সমান তাদের বিপরীত কোনগুলি সমান হয়] অর্থাৎ, ∠OCP + ∠PCQ = ∠OQP + ∠PQC [∵ ∠OCQ = ∠OCP + ∠PCQ এবং ∠OQC = ∠OQP + ∠PQC] ∴ ∠OQP + ∠PCQ = ∠OQP + ∠PQC [(iii) নং সমীকরনের মান বসিয়ে পেলাম] ∠PCQ = ∠PQC [(i) নং সমীকরন থেকে পাই]
এখন, যেহেতু ΔPCQ -এর ∠PCQ = ∠PQC ∴ CP = PQ [ত্রিভুজের যে দুটি বাহুর দৈর্ঘ্য সমান তাদের বিপরীত কোনগুলি সমান হয়] (প্রমানিত) |
koshe dekhi 7.2 class 10
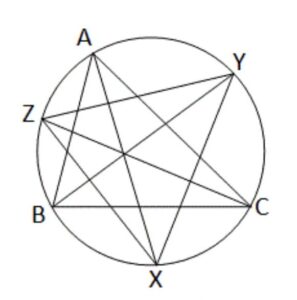
| Q9. একটি বৃত্তে ABC ত্রিভুজটি অন্তর্লিখিত। AX, BY এবং CZ যথাক্রমে ∠BAC, ∠ABC ও ∠ACB -এর সমদ্বিখণ্ডক এবং বৃত্তে যথাক্রমে X, Y, Z বিন্দুতে মিলিত হয়। প্রমাণ করি যে, AX, YZ এর উপর লম্ব।
সমাধান :
ΔABC বৃত্তের আন্তর্লিখিত। AX, BY এবং CZ যথাক্রমে ∠BAC, ∠ABC ও ∠ACB -এর সমদ্বিখন্ডক তিনটি যথাক্রমে X, Y, Z বিন্দুতে মিলিত হয় এবং আরো ধরি AX ও YZ পরস্পরকে P বিন্দুতে ছেদ করে। প্রমান করতে হবে যে, AX, YZ এর ওপর লম্ব। অঙ্কনঃ X, Y যুক্ত করা হল। প্রমানঃ AY উপচাপ দ্বারা গঠিত দুটি বৃত্তস্থ কোণ ∠AXY এবং ∠ABY ∴ ∠AXY = ∠ABY — (i) [একই বৃত্তচাপ দ্বারা গঠিত সকল বৃত্তস্থ কোণের মান সমান] আবার, BZ উপচাপ দ্বারা গঠিত দুটি বৃত্তস্থ কোণ ∠BYZ এবং ∠BCZ ∴ ∠BYZ = ∠BCZ — (ii) [একই বৃত্তচাপ দ্বারা গঠিত সকল বৃত্তস্থ কোণের মান সমান] আবার, BX উপচাপ দ্বারা গঠিত দুটি বৃত্তস্থ কোণ ∠BYX এবং ∠BAX ∴ ∠BYX = ∠BAX — (iii) [একই বৃত্তচাপ দ্বারা গঠিত সকল বৃত্তস্থ কোণের মান সমান]
এখন, ΔPXY -এর, ∠PYX + ∠PXY = ∠BYZ + ∠BYX + ∠AXY = ∠BCZ + ∠BAX + ∠ABY [(ii) ও (iii) নং সমীকরণ ব্যবহার করে পেলাম] = ½ ∠BCA + ½ ∠BAC+ ½ ∠ABC [AX, BY এবং CZ যথাক্রমে ∠BAC, ∠ABC ও ∠ACB -এর সমদ্বিখন্ডক] = ½ (∠BCA + ∠BAC + ∠ABC) = ½ × 180° [ত্রিভুজের তিনটি কোণের যোগফল 180°] = 90° ∴ ∠PYX + ∠PXY = 90° —–(iv)
এখন, ΔPXY -এর, ∠XPY = 180° – (∠PYX + ∠PXY) = 180° – 90° [(iv) নং সমীকরণ ব্যবহার করে পেলাম] = 90° অর্থাৎ, AX, YZ এর ওপর লম্ব। (প্রমানিত) |
koshe dekhi 7.2 class 10
| Q10. একটি বৃত্তে ABC ত্রিভুজটি অন্তর্লিখিত। ∠BAC, ∠ABC ও ∠ACB -এর সমদ্বিখণ্ডক বৃত্তে যথাক্রমে X, Y ও Z বিন্দুতে মিলিত হয়। প্রমাণ করি ΔXYZ এর, সমাধান :
ধরি, ΔABC ত্রিভূজটি বৃত্তে অন্তর্লিখিত। ∠BAC, ∠ABC ও ∠ACB এর সমদ্বিখন্ডক বৃত্তের যথাক্রমে X, Y ও Z বিন্দুতে মিলিত হয়।
প্রমান করতে হবে যে, ΔXYZ এর,
প্রমানঃ ΔABC -এর ∠ABC + ∠ACB = 180° – ∠BAC ——(i) AZ উপচাপ দ্বারা গঠিত দুটি বৃত্তস্থ কোণ ∠AXZ এবং ∠ACZ ∴ ∠AXZ = ∠ACZ ——- (ii) [একই বৃত্তচাপ দ্বারা গঠিত সকল বৃত্তস্থ কোণের মান সমান] AY উপচাপ দ্বারা গঠিত দুটি বৃত্তস্থ কোণ ∠YXA এবং ∠ABY ∴ ∠YXA = ∠ABY —— (iii) [একই বৃত্তচাপ দ্বারা গঠিত সকল বৃত্তস্থ কোণের মান সমান]
এখন, ΔXYZ -এর, ∠YXZ = ∠YXA + ∠AXZ বা, ∠YXZ = ∠ABY + ∠ACZ [(ii) এবং (iii) নং সমীকরণ ব্যবহার করে পেলাম] বা, বা, বা,
|
koshe dekhi 7.2 class 10
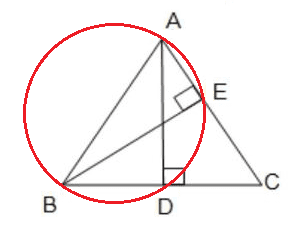
| Q11. ΔABC -এর A বিন্দু থেকে BC বাহুর উপর অঙ্কিত লম্ব BC বাহুকে D বিন্দুতে এবং B বিন্দু থেকে CA বাহুর উপর অঙ্কিত লম্ব CA বাহুকে E বিন্দুতে ছেদ করে। প্রমাণ করি যে, A, B, D, E বিন্দু চারটি সমবৃত্তস্থ।
সমাধান :
ΔABC এর A বিন্দু থেকে BC বাহুর উপর অঙ্কিত লম্ব BC বাহুকে D বিন্দুতে এবং B বিন্দু থেকে CA বাহুর উপর অঙ্কিত লম্ব CA বাহুকে Eবিন্দুতে ছেদ করে। প্রমান করতে হবে যে, A, B, D, E সমবৃত্তস্থ। অঙ্কনঃ D, E যুক্ত করা হল। প্রমানঃ ΔEBC এবং ΔADC থেকে পাই, ∠BEC = ∠ADC [প্রতিটি কোণের মান 1 সমকোণ] ∠ECD সাধারন কোণ ∴ অবশিষ্ট ∠EBC = অবশিষ্ট ∠DAC অর্থাৎ, ∠EBD = ∠DAE যেহেতু, DE সরল রেখাংশের একই পার্শ্বে অপর দুই বিন্দু B এবং A তে দুটি সমান কোণ উৎপন্ন হয়েছে, তাই A, B, D, E সমবৃত্তস্থ। (প্রমানিত) |
koshe dekhi 7.2 class 10
| Q12. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
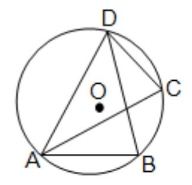
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) : (i) পাশের চিত্রে O বৃত্তের কেন্দ্র; ∠ACB = 30°, ∠ABC = 60°, ∠DAB = 35° এবং ∠DBC = x° হলে, x -এর মান (a) 35 (b) 70 (c) 65 (d) 55 উত্তরঃ সঠিক নির্বাচনটি হবে (d) 55
|
| Q12. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
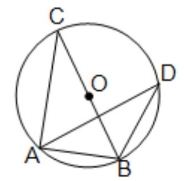
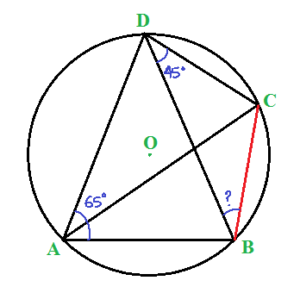
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) : (ii) পাশের চিত্রে O বৃত্তের কেন্দ্র। ∠BAD = 65°, ∠BDC = 45° হলে, ∠CBD -এর মান (a) 65° (b) 45° (c) 40° (d) 20° উত্তরঃ সঠিক নির্বাচনটি হবে (d) 20°
|
koshe dekhi 7.2 class 10
| Q12. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
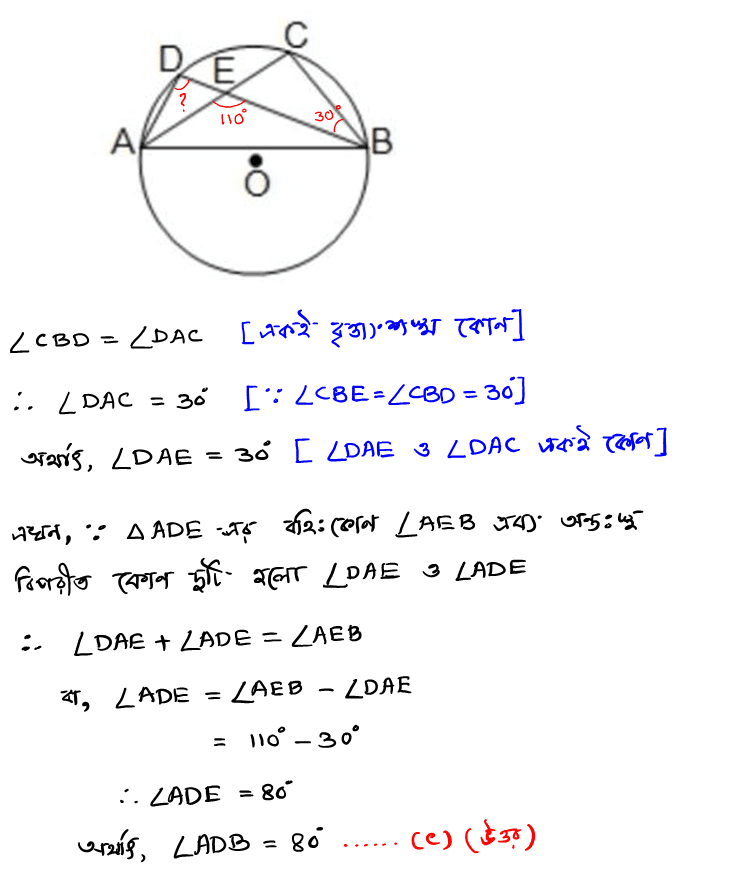
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) : (iii) পাশের চিত্রে O বৃত্তের কেন্দ্র। ∠AEB = 110° এবং ∠CBE = 30° হলে, ∠ADB -এর মান (a) 70° (b) 60° (c) 80° (d) 90° উত্তরঃ সঠিক নির্বাচনটি হবে (c) 80°
|
koshe dekhi 7.2 class 10
koshe dekhi 7.2 class 10
| Q12. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
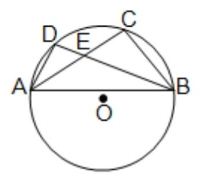
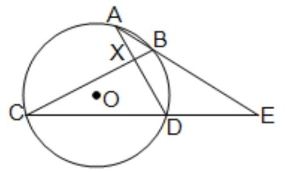
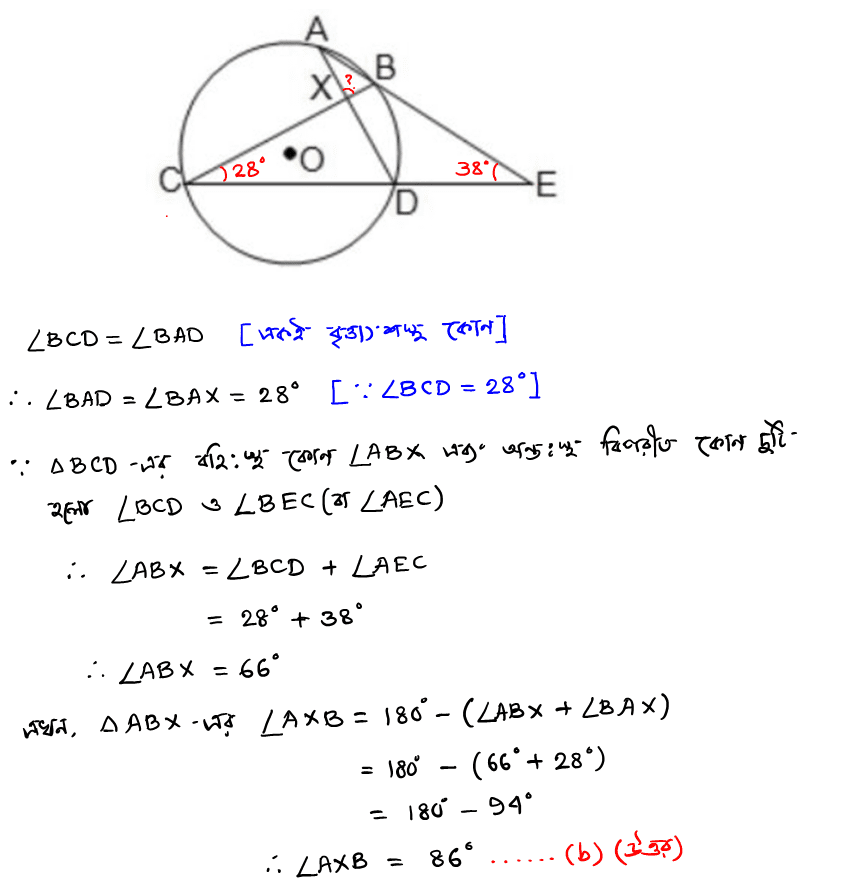
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) : (iv) পাশের চিত্রে O বৃত্তের কেন্দ্র। ∠BCD = 28°, ∠AEC = 38° হলে, ∠AXB -এর মান (a) 56° (b) 86° (c) 38° (d) 28° উত্তরঃ সঠিক নির্বাচনটি হবে (b) 86°
|
Support Me
If you like my work then you can Support me by contributing a small amount which will help me a lot to grow my channel. It’s a request to all of you. You can donate me through phone pay / Paytm/ Gpay on this number 7980608289 or by the link below :
koshe dekhi 7.2 class 10
koshe dekhi 7.2 class 10
| Q12. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
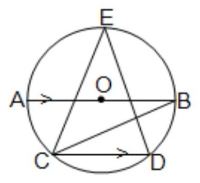
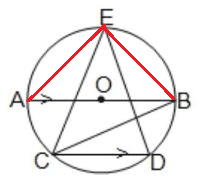
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) : (v) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB ব্যাস। AB ∥ CD. ∠ABC = 25° হলে, ∠CED -এর মান (a) 80° (b) 50° (c) 25° (d) 40° উত্তরঃ সঠিক নির্বাচনটি হবে (d) 40°
|
koshe dekhi 7.2 class 10
| 12 (B) সত্য বা মিথ্যা লিখি :
(i) পাশের চিত্রে AD ও BE যথাক্রমে ABC ত্রিভুজের BC ও AC বাহুর উপর লম্ব। A, B, D, E বিন্দু চারটি সমবৃত্তস্থ। উত্তরঃ প্রদত্ত বিবৃতিটি সত্য।
|
Support Me
If you like my work then you can Support me by contributing a small amount which will help me a lot to grow my channel. It’s a request to all of you. You can donate me through phone pay / Paytm/ Gpay on this number 7980608289 or by the link below :
| 12 (B) সত্য বা মিথ্যা লিখি :
(ii) ABC ত্রিভুজের AB = AC ; BE ও CF যথাক্রমে ∠ABC ও ∠ACB -এর সমদ্বিখণ্ডক এবং AC ও AB বাহুকে যথাক্রমে E ও F বিন্দুতে ছেদ করে। B, C, E, F বিন্দু চারটি সমবৃত্তস্থ নয়। উত্তরঃ প্রদত্ত বিবৃতিটি মিথ্যা।
|
koshe dekhi 7.2 class 10
| 12 (C) শূন্যস্থান পূরণ করি :
(i) একই বৃত্তাংশস্থ বৃত্তস্থ কোণ _______। উত্তরঃ একই বৃত্তাংশস্থ বৃত্তস্থ কোণ সমান।
12 (C) শূন্যস্থান পূরণ করি : (ii) দুটি বিন্দুর সংযোজক সরলরেখাংশ তার একই পার্শ্বে অপর দুটি বিন্দুতে সমান সম্মুখ কোণ উৎপন্ন করলে বিন্দু চারটি _______ হবে। উত্তরঃ দুটি বিন্দুর সংযোজক সরলরেখাংশ তার একই পার্শ্বে অপর দুটি বিন্দুতে সমান সম্মুখ কোণ উৎপন্ন করলে বিন্দু চারটি সমবৃত্তস্থ হবে।
12 (C) শূন্যস্থান পূরণ করি : (iii) একই বৃত্তে দুটি চাপ দ্বারা উৎপন্ন বৃত্তস্থ কোণ দুটি সমান হলে চাপ দুটির দৈর্ঘ্য _______। উত্তরঃ একই বৃত্তে দুটি চাপ দ্বারা উৎপন্ন বৃত্তস্থ কোণ দুটি সমান হলে চাপ দুটির দৈর্ঘ্য সমান হবে । |
koshe dekhi 7.2 class 10
| Q13. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)
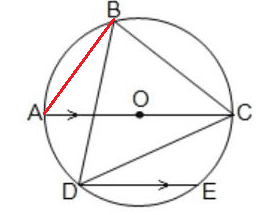
(i) পাশের চিত্রে O বৃত্তের কেন্দ্র, AC ব্যাস এবং জ্যা DE ও ব্যাস AC সমান্তরাল। ∠CBD = 60° হলে, ∠CDE -এর মান নির্ণয় করি। উত্তরঃ ∠CDE = 30°
|
koshe dekhi 7.2 class 10
| Q13. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)
(ii) পাশের চিত্রে ∠PQR -এর সমদ্বিখণ্ডক QS; ∠SQR = 35° এবং ∠PRQ = 32° হলে , ∠QSR -এর মান নির্ণয় করি। উত্তরঃ ∠QSR = 78°
|
koshe dekhi 7.2 class 10
koshe dekhi 7.2 class 10
| Q13. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)
(iii) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB ব্যাস। AB ও CD পরস্পর লম্ব এবং ∠ADC = 50° ; ∠CAD -এর মান নির্ণয় করি। উত্তরঃ ∠CAD = 80°
|
koshe dekhi 7.2 class 10
koshe dekhi 7.2 class 10
| Q13. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)
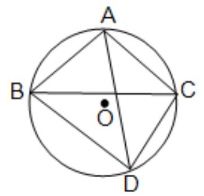
(iv) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB = AC; ∠ABC = 32° হলে, ∠BDC -এর মান নির্ণয় করি। উত্তরঃ ∠BDC = 64°
|
| Q13. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)
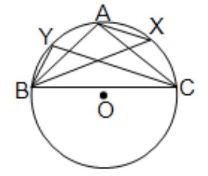
(v) পাশের চিত্রে BX ও CY যথাক্রমে ∠ABC ও ∠ACB -এর সমদ্বিখণ্ডক। AB = AC এবং BY = 4 সেমি. হলে, AX -এর দৈর্ঘ্য নির্ণয় করি। উত্তরঃ AX -এর দৈর্ঘ্য 4 সেমি।
|
Koshe Dekhi 7.2 Class 10
Support Me
If you like my work then you can Support me by contributing a small amount which will help me a lot to grow my Website. It’s a request to all of you. You can donate me through phone pay / Paytm/ Gpay on this number 7980608289 or by the link below :
and visit Our website : learningscience.co.in
গণিত প্রকাশ (দশম শ্রেণী) সম্পূর্ণ সমাধান
গণিত প্রকাশ (নবম শ্রেণী) সম্পূর্ণ সমাধান
গণিত প্রভা (ষষ্ঠ শ্রেণী) সম্পূর্ণ সমাধান
জীবন বিজ্ঞান (দশম শ্রেণী) (Life Science)