SSC CGL Held on 8th August 2017 Shift 3

SSC CGL Held on 8th August 2017 Shift 3
Staff Selection Commission – Combined Graduate Level Examination, often referred to as SSC CGL is an examination conducted to recruit staff to various posts in ministries, departments and organisations of the Government of India. It is conducted by the Staff Selection Commission for selecting staff for various Group B and Group C posts. The Staff Selection Commission was established in 1975.
Candidates applying for the various posts need to have a bachelor’s degree from a recognised university at the time of applying. Age of the candidate must be between 18 and 32 years (depending upon post applied).
For more click here.
Q.1) Which one is the largest among the fractions 5⁄113 , 7⁄120 , 13⁄145 and 17⁄160 ?
a) 5⁄113
b) 7⁄120
c) 13⁄145
d) 17⁄160
Answer
Correct Answer: (d) 17⁄160
Solution
We have,
5⁄113 = 0.044….
7⁄120 = 0.058….
13⁄145 = 0.089….
17⁄160 = 0.106….
Therefore, the required largest fraction = 17⁄160 (Ans.)
Q.2) Nirmit can do 2⁄3 of a job in 18 days. Kashish is twice as efficient as Nirmit. In how many days Kashish will complete the job ?
a) 29⁄4
b) 27⁄2
c) 31⁄2
d) 13⁄2
Answer
Correct Answer: (b) 27⁄2
Solution
Let, total job be 1 part.
As given, Nirmit can do 2⁄3 of a job in 18 days.
Therefore, Nirmit can complete the job in ( 18 × 3⁄2 ) = 27 days.
Again, Kashish is 2 times efficient than Nirmit.
Hence, Kashish will take = 27⁄2 days to complete the whole job. (Ans.)
Note : Efficient means less time to do a job.
Q.3) 40 men took a dip in a pool 30 m long and 25 m broad. If the average water displaced by a man is 5 m3, then what will be the rise (in cm) in level of the pool ?
a) 25
b) 26.66
c) 27.33
d) 28
Answer
Correct Answer: (b) 26.66
Solution
As given, one man can displaced volume of water = 5 m3
Therefore, 40 men can displaced volume of water = 5 × 40 = 200 m3
Now, rise in level of the pool,
= volume of water⁄(length × breadth)
= 200 m3⁄(30 m × 25 m)
= 0.2666 m (approx)
= 26.66 cm (approx) (Ans.)
Q.4) An article is listed at Rs 2375. A man purchases it at two successive discounts of 50% and 25% and spends Rs 165 on repairing of article. If he sells the article at a profit of 62.5%, then what is the selling price (in Rs) of the article ?
a) 1467.6
b) 1492.6
c) 1715.39
d) 1467.6
Answer
Correct Answer: (c) 1715.39
Solution
Net discount = [ 50 + 25 − (50 × 25)⁄100 ] = 62.5 %
Note :
(1) If x and y are two successive discount then total discount percentage = [ x + y − (x × y)⁄100 ]
(2) If x and y are two successive gain then total gain percentage = [ x + y + (x × y)⁄100 ]
He purchases the article at,
= Rs. 2375 × (100 − 62.5)⁄100
= Rs. 890.625
Repairing Cost = Rs. 165
Therefore, actual cost price (C.P.) of the article = Rs. (890.625 + 165) = Rs. 1055.625
His profit percentage = 62.5 %, ⇒ C.P. = 100 and S.P. = 100 + 62.5 = 162.5
Hence, required selling price (S.P.) of the article,
= Rs. [ (actual S.P.) × ( S.P.⁄C.P. ) ]
= Rs. 1055.625 × (100 + 62.5)⁄100
= Rs. 1715.39 (Ans.)
Q.5) The length, breadth and height of a cuboid are in the ratio 19 : 11 : 13. If length is 30 cm more than height, then what is the volume (in cm3) of this cuboid ?
a) 81510
b) 89665
c) 195300
d) 339625
Answer
Correct Answer: (d) 339625
Solution
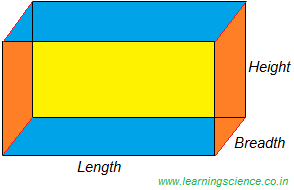
Let, length, breadth, and height of the cuboid is be 19x cm, 11x cm, and 13x cm respectively.
Now, according to the statement of the question, we have
19x = 13x + 30
⇒ x = 5
∴ Length = 19 × 5 = 95 cm
Breadth = 11 × 5 = 55 cm and
Height = 13 × 5 = 65 cm
We know, volume of a cuboid = length × breadth × height
= 95 cm × 55 cm × 65 cm
= 339625 cm3 (Ans.)
Q.6) Average age of a team having 12 players is 23 years. If the age of the coach is also included, then the average age increases by 2 years. What is the age (in years) of the coach ?
a) 41
b) 47
c) 49
d) 51
Answer
Correct Answer: (c) 49
Solution
Shortcut Approach :
∵ Average age is increased by 2 years among 13 members after joining the coach.
Therefore, Age of the coach,
= (13 × 2 + 23 ) years
= 49 years. (Ans.)
Q.7) An item is sold at two successive gains of 30% and 20%. If the final selling price is Rs 31200, then what is the cost price (in Rs) ?
a) 15000
b) 20000
c) 22250
d) 24000
Answer
Correct Answer: (b) 20000
Solution
Net gain = [ 30 + 20 + (30 × 20)⁄100 ] = 56 %
Note :
(1) If x and y are two successive gain then total gain percentage = [ x + y + (x × y)⁄100 ]
(2) If x and y are two successive discount then total discount percentage = [ x + y − (x × y)⁄100 ]
In 56 % gain, cost price (C.P.) = 100 and selling price (S.P.) = 100 + 56 = 156
Hence, required C.P. of the item,
= Rs. [ (actual C.P.) × ( C.P.⁄S.P. ) ]
= Rs. 31200 × 100⁄156
= Rs. 20,000 (Ans.)
Q.8) The number of trees in a town is 17640. If the numbers of trees increases annually at the rate of 5%, then how many trees were there 2 years ago ?
a) 14000
b) 15000
c) 16000
d) 19450
Answer
Correct Answer: (c) 16000
Solution
Given,
The number of trees at present (P) = 17640
Rate of increase (annually) (r) = 5 %
Time (t) = 2 years
Therefore,
The number of trees before 2 years,
= P [ 100⁄( 100 + r ) ] t
= 17640 [ 100⁄( 100 + 5 ) ] 2
= 17640 × 100⁄105 × 100⁄105
= 16,000 (Ans.)
Note :
If the question is asked for “the number after ‘t’ years“, then the required number will be = P [ ( 100 ± r )⁄100 ] t
but,
If the question is asked for “the number before ‘t’ years“, then the required number will be = P [ 100⁄( 100 ± r ) ] t
Where ‘+’ for rate of increase and ‘−’ for rate of decrease.
Q.9) Aman and Kapil starts from Delhi and Gwalior respectively towards each other at same time. They meet at Mathura and then take 196 minutes and 225 minutes respectively to reach Gwalior and Delhi. If speed of Aman is 30 km/hr, then what is the speed (in km/hr) of Kapil ?
a) 28
b) 30
c) 225⁄7
d) 392⁄15
Answer
Correct Answer: (a) 28
Solution
Given,
Time taken by Aman to reach Gwalior from their meeting point (i.e. Mathura) = 196 minutes and
Time taken by Kapil to reach Delhi from Mathura = 225 minutes
Let, time taken by both of them to reach Mathura from their respective starting points = ‘t’ minutes.
∴ t = √(196 × 225)
⇒ t = 14 × 15 = 210 minutes.
Now,
Total time taken by Aman to reach Gwalior from Delhi = 196 + 210 = 406 minutes and
Total time taken by Kapil to reach Delhi from Gwalior = 225 + 210 = 435 minutes
As, speed of Aman = 30 km/hr = 30⁄60 km/minutes = 0.5 km/min
Distance between Gwalior to Delhi = Speed × Time = 0.5 × 406 = 203 km
∴ Speed of Kapil = Distance⁄Time
= 203 km⁄435 min
= ( 203 × 60 ) km⁄435 hr = 28 km/hr (Ans.)
Q.10) The simple interest on a sum of money for 10 years is Rs 3130. If the principal becomes 5 times after 5 years, then what will be the total interest (in Rs) obtained after 10 years ?
a) 6260
b) 7825
c) 9390
d) 15650
Answer
Correct Answer: (c) 9390
Solution
Shortcut Approach :
Given,
Simple Interest (S.I.) for 10 years = Rs. 3130
We know that, S.I. is same at every year.
Therefore, S.I. at the end of the 5 year,
= Rs. 3130⁄10 × 5 = Rs. 1565
If principal becomes 5 times after 5 years then S.I. for the remaining 5 years also becomes 5 times i.e. Rs. (5 × 1565) = Rs. 7825
Therefore, total interest obtained after 10 years,
= Rs.(7825 + 1565)
= Rs. 9390 (Ans.)
Q.11) If (11 − 13x)⁄x + (11 − 13y)⁄y + (11 − 13z)⁄z = 5 , then what is the value of 1⁄x + 1⁄y + 1⁄z ?
a) 1
b) 13⁄11
c) 13⁄
d) 4
Answer
Correct Answer: (d) 4
Solution
Given,
(11 − 13x)⁄x + (11 − 13y)⁄y + (11 − 13z)⁄z = 5
⇒ 11⁄x − 13 + 11⁄y − 13 + 11⁄z − 13 = 5
⇒ 11 (1⁄x + 1⁄y + 1⁄z) = 5 + 39
⇒ 1⁄x + 1⁄y + 1⁄z = 4 (Ans.)
Q.12) If 2x + 9⁄x = 9, then what is the minimum value of x2 + 1⁄x2 ?
a) 95⁄36
b) 97⁄36
c) 86⁄25
d) 623⁄27
Answer
Correct Answer: (b) 97⁄36
Solution
Given,
2x + 9⁄x = 9
⇒ 2x2 + 9 = 9x
⇒ 2x2 − 9x + 9 = 0
⇒ (x − 3)(2x − 3) = 0
Now,
either, (x − 3) = 0 ⇒ x = 3
or, (2x − 3) = 0 ⇒ x = 3⁄2
Now, if we take x = 3, then the required
x2 + 1⁄x2
= 32 + 1⁄32
= 9 + 1⁄9
= 82⁄9 (but there has no such option in the given question)
But, if we take x = 3⁄2 , then the required
x2 + 1⁄x2
= ( 3⁄2 )2 + ( 2⁄3 )2
= 9⁄4 + 4⁄9
= 97⁄36 (Ans.)
Q.13) If (5x − y)⁄(5x + y) = 3⁄7, then what is the value of (4x2 + y2 − 4xy)⁄(9x2 + 16y2 + 24xy) ?
a) 0
b) 3⁄7
c) 18⁄49
d) 1⁄6
Answer
Correct Answer: (a) 0
Solution
Given,
(5x − y)⁄(5x + y) = 3⁄7
or, 7 (5x − y) = 3 ( 5x + y)
or, 35x − 7y = 15x + 3y
or, 35x − 15x = 3y + 7y
or, 20x = 10y
or, 2x = y
Now, the value of numerator part in the required question means,
4x2 + y2 − 4xy
= 4x2 + (2x)2 − 4.x.(2x)
= 4x2 + 4x2 − 8x2
= 0
Therefore, the required value of (4x2 + y2 − 4xy)⁄(9x2 + 16y2 + 24xy) = 0 (Ans.)
Q.14) If (x + y)2 = xy + 1 and x3 − y3 = 1, then what is the value of x − y ?
a) 1
b) 0
c) − 1
d) 2
Answer
Correct Answer: (a) 1
Solution
Given,
(x + y)2 = xy + 1
⇒ x2 + 2xy + y2 = xy + 1
⇒ x2 + xy + y2 = 1
⇒ (x − y)(x2 + xy + y2) = 1 × (x − y) [multiplying by (x − y) both sides]
⇒ x3 − y3 = x − y
⇒ 1 = x − y [∵ given, x3 − y3 = 1]
Therefore, the required value of (x − y) = 1 (Ans.)
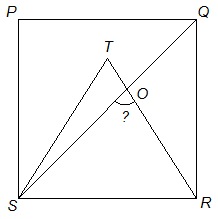
Q.15) In the given figure, PQRS is a square and SRT is an equilateral triangle. What is the value (in degrees) of ∠SOR ?
a) 45
b) 55
c) 60
d) 75
Answer
Correct Answer: (d) 75
Solution

As, we know that diagonal of a square bisects its angle.
Therefore, ∠RSQ = 45°
Again, as ∆SRT is an equilateral triangle.
Therefore, ∠SRT = 60°
Now, in ∆SOR,
∠SOR + ∠OSR + ∠SRO = 180° [using angle sum property of triangle]
⇒ ∠SOR + 45° + 60° = 180°
∴ ∠SOR = 75° (Ans.)
Q.16) ABCD is a parallelogram in which AB = 7 cm, BC = 9 cm and AC = 8 cm. What is the length (in cm) of other diagonal ?
a) 14
b) 14√2
c) 7
d) 7√2
Answer
Correct Answer: (a) 14
Solution
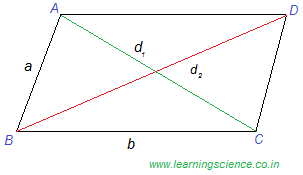
We can easily prove that,
d12 + d22 = 2 (a2 + b2)
where,
d1 and d2 are two diagonals and ‘a‘ and ‘b‘ are two sides.
Note: The above formula is valid for all type quadrilateral like ‘Parallelogram‘; ‘Rhombus‘; ‘Rectangle‘; ‘Square‘ and ‘Kite‘ but not for irregular quadrilateral and ‘Trapezium‘.

Now given,
d1 = 8 cm, d2 = ?, a = AB = 7 cm and b = BC = 9 cm
Therefore, according to the above formula, we have
82 + d12 = 2 ( 72 + 92 )
⇒ d12 = 196
⇒ d1 = √196 = 14 cm (Ans.)
Q.17) How many diagonals are there in octagon ?
a) 12
b) 14
c) 20
d) 24
Answer
Correct Answer: (c) 20
Solution
Number of diagonals = n(n − 3)⁄2 where, n = number of sides
In an Octagon, n = 8
Therefore, the required number of diagonals in an Octagon,
= 8(8 − 3)⁄2
= 20 (Ans.)
Q.18) A square is inscribed in a quarter circle in such a way that two of its adjacent vertices on the radius are equidistant from the centre and other two vertices lie on the circumference. If the side of square is √(5/2) cm, then what is the radius (in cm) of the circle ?
a) 2
b) 2.5
c) 5
d) 10
Answer
Correct Answer: (b) 2.5
Solution

Let, O be the center of the circle and SPQR is a square inscribed in it in such a way that points S and P are equidistant from center ‘O’ means OS = OP = x (say)
∠PSQ = 45° [diagonal of square bisects the angle]
Again, ∆SOP is an isosceles right-angled triangle.
Therefore, ∠OSP = 45°
Now, ∠OSQ = ∠OSP + ∠PSQ = 45° + 45°
∠OSQ = 90°
Now, in ∆SOP, we have
SP2 = OS2 + OP2 [applying Pythagoras theorem]
⇒ √(5⁄2)2 = x2 + x2
∴ x2 = 5⁄4
Now, diagonal of square, SQ = side √2 = √(5⁄2) × √2 = √5 cm.
Again, in right-angled ∆SOQ, we have
OQ2 = OS2 + SQ2 [applying Pythagoras theorem]
⇒ OQ2 = x2 + (√5)2
⇒ OQ2 = 5⁄4 + (√5)2
⇒ OQ = 5⁄2 cm. = 2.5 cm
∴ The required radius of the circle = 2.5 cm. (Ans.)
Q.19) If sec2θ + tan2θ = 5⁄3, then what is the value of tan 2θ ?
a) 2√3
b) √3
c) 1⁄√3
d) cannot be determined
Answer
Correct Answer: (b) √3
Solution
Given,
sec2θ + tan2θ = 5⁄3
⇒ 1 + tan2θ + tan2θ = 5⁄3 [since, sec2θ = 1 + tan2θ]
⇒ 3 + 6 tan2θ = 5
⇒ 6 tan2θ = 2
⇒ tan θ = 1⁄√3 ⇒ θ = 30°
Now, tan 2θ = tan (2 × 30)° = tan 60° = √3 (Ans.)
Q.20) A tower is broken at a point P above the ground. The top of the tower makes an angle 60° with the ground at Q. From another point R on the opposite side of Q angle of elevation of point P is 30°. If QR = 180 m, then what is the total height (in metres) of the tower ?
a) 90
b) 45√3
c) 45(√3 + 1)
d) 45(√3 + 2)
Answer
Correct Answer: (d) 45(√3 + 2)
Solution
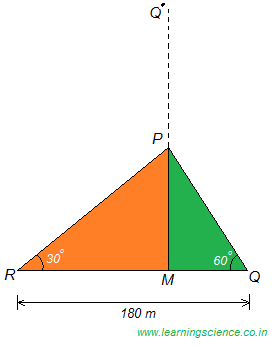
Let, MQ’ be the height of the tower.
In right-angled ∆PMQ,
PM⁄MQ = tan 60° ⇒ √3
Therefore, PM = √3 MQ
Again, in right-angled ∆PMR,
PM⁄RM = tan 30° ⇒ 1⁄√3
⇒ √3 PM = RM
⇒ √3.(√3 MQ) = RM
Therefore, RM = 3MQ
Now, Given
RQ = 180 m
⇒ RM + MQ = 180
⇒ 3MQ + MQ = 180
Therefore, MQ = 45 m
Therefore, PM = √3 MQ ⇒ √3 × 45 m
Again, in right-angled ∆PMQ,
MQ⁄PQ = cos 60° ⇒ 1⁄2
⇒ PQ = 2MQ ⇒ 2 × 45 = 90 m
We know that, PQ = PQ’ = 90 m
Therefore, the required height of the tower,
MQ’ = MP + PQ’
= √3 × 45 m + 90 m
= 45 (√3 + 2) m
MQ’ = 45 (√3 + 2) m (Ans.)
Q.21) If sin θ + sin 5θ = sin 3θ and 0 < θ < π⁄2, then what is the value of θ (in degrees) ?
a) 30°
b) 45°
c) 60°
d) 75°
Answer
Correct Answer: (a) 30°
Solution
Given,
sin θ + sin 5θ = sin 3θ
2 sin{ ( 5θ + θ )⁄2 } × cos{ ( 5θ − θ )⁄2 } = sin 3θ [using the formula, sin C + sin D = 2 sin{ ( C + D )⁄2 } × cos{ ( C − D )⁄2 }]
⇒ 2 sin 3θ × cos 2θ = sin 3θ
⇒ sin 3θ (2 cos 2θ − 1) = 0
Now,
Either, sin 3θ = 0 ⇒ θ = 0° [the value of θ is not acceptable because of the given condition i.e. 0 < θ < π⁄2 ]
Or, (2 cos 2θ − 1) = 0
⇒ cos 2θ = 1⁄2 ⇒ cos 60°
⇒ 2θ = 60°
∴ θ = 30° (Ans.)
Q.22) The table below represent the cost, revenue and tax rate for XYZ Ltd. for a period of 8 years. Cost and revenue are given in Rs. ‘000 crores.
Profit for any year = revenue − cost
Profit after tax for any year = profit of that year − tax of that year
Tax on any year = tax rate of that year × profit of the year
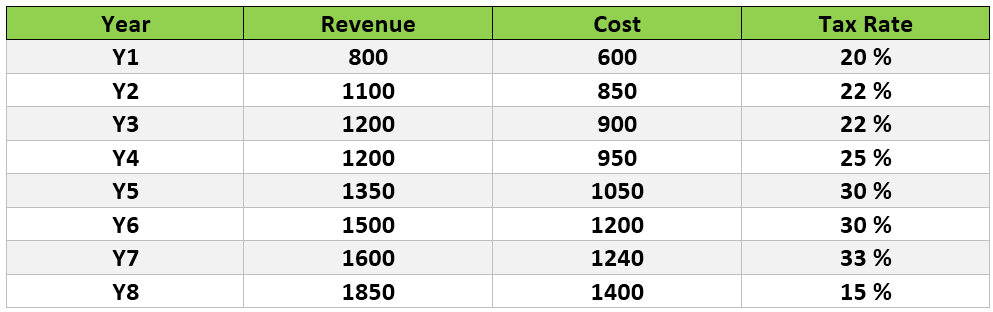
How much tax (in Rs ‘000 crores) was paid by XYZ limited in Y7 ?
a) 90
b) 99
c) 118.8
d) 126
Answer
Correct Answer: (c) 118.8
Solution

Tax (in Rs. ‘000 crores) was paid by XYZ Ltd. in Y7,
= tax rate for Y7 × (revenue − cost) for Y7
= 33 % × (1600 − 1240 )
= 33⁄100 × 360
= 118.8 (Ans.)
Q.23) The table below represent the cost, revenue and tax rate for XYZ Ltd. for a period of 8 years. Cost and revenue are given in Rs. ‘000 crores.
Profit for any year = revenue − cost
Profit after tax for any year = profit of that year − tax of that year
Tax on any year = tax rate of that year × profit of the year

Which of the following is correct about profit after tax for year Y2, Y6 and Y8 ?
a) Y8 > Y6 = Y2
b) Y6 > Y2 > Y8
c) Y8 > Y6 > Y2
d) Y6 = Y8 > Y2
Answer
Correct Answer: (c) Y8 > Y6 > Y2
Solution

Calculation of Profit after Tax :
Tax (in Rs. ‘000 crores) for Y2,
= 22 % × (1100 − 850)
= 22⁄100 × 250
= 55
Therefore, Profit (in Rs. ‘000 crores) after tax for Y2,
= (1100 − 850) − (55)
= 195
Similarly,
Profit (in Rs. ‘000 crores) after tax for Y6,
= (1500 − 1200) − (90)
= 210
Profit (in Rs. ‘000 crores) after tax for Y8,
= (1850 − 1400) − (67.5)
= 382.5
Conclusion:
Y8 > Y6 > Y2 (Ans.)
Q.24) The table below represent the cost, revenue and tax rate for XYZ Ltd. for a period of 8 years. Cost and revenue are given in Rs. ‘000 crores.
Profit for any year = revenue − cost
Profit after tax for any year = profit of that year − tax of that year
Tax on any year = tax rate of that year × profit of the year

How many distinct values of yearly profit are there ?
a) 3
b) 4
c) 5
d) 6
Answer
Correct Answer: (c) 5
Solution

Calculation of Profit for any year :
Profit (in Rs. ‘000 crores) for Y1 = 800 − 600 = 200
Profit (in Rs. ‘000 crores) for Y2 = 1100 − 850 = 250
Profit (in Rs. ‘000 crores) for Y3 = 1200 − 900 = 300
Profit (in Rs. ‘000 crores) for Y4 = 1200 − 950 = 250
Profit (in Rs. ‘000 crores) for Y5 = 1350 − 1050 = 300
Profit (in Rs. ‘000 crores) for Y6 = 1500 − 1200 = 300
Profit (in Rs. ‘000 crores) for Y7 = 1600 − 1240 = 360
Profit (in Rs. ‘000 crores) for Y8 = 1850 − 1400 = 450
Now, we can see from the above data, there are 5 different values of profit on any year which are 200, 250, 300, 360 and 450.
So, there are 5 distinct values of profit. (Ans.)
Note :
Distinct Number : The term distinct number is used to refer to a number in a set that is not equal to another number.
Q.25) The table below represent the cost, revenue and tax rate for XYZ Ltd. for a period of 8 years. Cost and revenue are given in Rs. ‘000 crores.
Profit for any year = revenue − cost
Profit after tax for any year = profit of that year − tax of that year
Tax on any year = tax rate of that year × profit of the year

What is the total sum (in ‘000 crores) of profit after tax for Y1 to Y8 ?
a) 1763.6
b) 1803.2
c) 1820.2
d) 1872.4
Answer
Correct Answer: (c) 1820.2
Solution

Calculation of Profit after Tax :
Tax (in Rs. ‘000 crores) for Y1,
= 20 % × (800 − 600)
= 20⁄100 × 200
= 40
Therefore, Profit (in Rs. ‘000 crores) after tax for Y1,
= (800 − 600) − (40)
= 160
Similarly,
Profit (in Rs. ‘000 crores) after tax for Y2,
= (1100 − 850) − (55)
= 195
Profit (in Rs. ‘000 crores) after tax for Y3,
= (1200 − 900) − (66)
= 234
Profit (in Rs. ‘000 crores) after tax for Y4,
= (1200 − 950) − (62.5)
= 187.5
Profit (in Rs. ‘000 crores) after tax for Y5,
= (1350 − 1050) − (90)
= 210
Profit (in Rs. ‘000 crores) after tax for Y6,
= (1500 − 1200) − (90)
= 210
Profit (in Rs. ‘000 crores) after tax for Y7,
= (1600 − 1240) − (118.8)
= 241.5
Profit (in Rs. ‘000 crores) after tax for Y8,
= (1850 − 1400) − (67.5)
= 382.5
Therefore, net profit (in Rs. ‘000 crores) after tax for Y1 to Y8,
= 160 + 195 + 234 + 187.5 + 210 + 210 + 241.5 + 382.5
= 1820.5 (Ans.)
If you still have any query then feel free to contact or comment below. I will definitely try to solve your issue. Thank you.
SSC CGL Held on 8th August 2017 Shift 3, SSC CGL Held on 8th August 2017 Shift 3, SSC CGL Held on 8th August 2017 Shift 3, SSC CGL Held on 8th August 2017 Shift 3, SSC CGL Held on 8th August 2017 Shift 3, SSC CGL Held on 8th August 2017 Shift 3, SSC CGL Held on 8th August 2017 Shift 3, SSC CGL Held on 8th August 2017 Shift 3, SSC CGL Held on 8th August 2017 Shift 3, SSC CGL Held on 8th August 2017 Shift 3,