SSC CGL Held on 8th August 2017 Shift 2

SSC CGL Held on 8th August 2017 Shift 2
Staff Selection Commission – Combined Graduate Level Examination, often referred to as SSC CGL is an examination conducted to recruit staff to various posts in ministries, departments and organisations of the Government of India. It is conducted by the Staff Selection Commission for selecting staff for various Group B and Group C posts. The Staff Selection Commission was established in 1975.
Candidates applying for the various posts need to have a bachelor’s degree from a recognised university at the time of applying. Age of the candidate must be between 18 and 32 years (depending upon post applied).
For more click here.
Q.1) What least value which should be added to 1812 to make it divisible by 7, 11 and 14 ?
a) 12
b) 36
c) 72
d) 154
Answer
Correct Answer: (b) 36
Solution
L.C.M. of 7, 11, 14 = 154
Now,

∴ The required minimum number should be added to 1812 to make it (i.e. 1812) completely divisible by 7, 11 and 14,
= Divisor − Remainder = 154 − 118 = 36 (Ans.)
Q.2) A is 1.5 times efficient than B therefore takes 8 days less than B to complete a work. If A and B work on alternate days and A works on first day, then in how many days the work will be completed ?
a) 17
b) 19
c) 19.5
d) 21
Answer
Correct Answer: (b) 19
Solution
Shortcut Approach:
Let, B can do a job in 3x days
As efficiency of A is 1.5 times more than B. Therefore A can do the same job in 2x days. [2x × 1.5 = 3x]
Now, according to the statement of the question given, we have,
3x − 2x = 8
∴ x = 8
∴ B will take 8 × 3 = 24 days and A will take 8 × 2 = 16 days to complete the same job separately.
Now, L.C.M. of 24 and 16 = 48
Let, total work = 48 units.
∴ At 1st day A works = 48⁄16 = 3 units
∴ In 2nd day B works = 48⁄24 = 2 units
Now, at the end of the 2nd day, amount of work which has been completed = 3 + 2 = 5 units
Therefore, In 18 days (= 2 × 9), amount of work that has been completed = 5 × 9 = 45 units
∴ Remaining work = 48 − 45 = 3 units which will be completed by the A in 1 day. [since A starts first]
Therefore, the required total days to complete the whole job = 18 + 1 = 19 days. (Ans.)
Q.3) One of the diagonal of a rhombus is 70% of the other diagonal. What is the ratio of area of rhombus to the square of the length of the larger diagonal ?
a) 3 : 10
b) 3 : 20
c) 7 : 20
d) 7 : 10
Answer
Correct Answer: (c) 7 : 20
Solution
Let, diagonals of rhombus are p and q. [ assuming p > q ]
Therefore, length of each side of square = p [as per the question given]
Again, q = 70 % of p
Therefore, q = p × 70⁄100 = 7p⁄10
Now, the ratio of area of rhombus to the square, we have
pq⁄2 : p2
⇒ q : 2p
⇒ 7p⁄10 : 2p
⇒ 7 : 20 (Ans.)
Q.4) A shopkeeper sells a table at a discount of 20% and earns a profit of 60%. If he sells the same table at 40% discount, then what will be his new profit percent ?
a) 20
b) 30
c) 35
d) 40
Answer
Correct Answer: (a) 20
Solution
Let, C.P. of a table be ‘x’
∴ At 60 % profit, S.P. = 160x⁄100 = 8x⁄5
At 20 % discount, S.P. = 100 − 20 = 80
Therefore, C.P. of a table = 80 × x⁄( 8x⁄5 ) = Rs. 50
At 40 % discount S.P. = 100 − 40 = 60
Therefore, Profit = 60 − 50 = 10
Now, at 40 % discount, percentage of profit,
= profit⁄C.P. × 100
= 10⁄50 × 100 = 20 % (Ans.)
Q.5) If A⁄3 = B⁄2 = C⁄5 , then what is the value of ratio (C + A)2 : (A + B)2 : (B + C)2 ?
a) 9 : 4 : 25
b) 25 : 4 : 9
c) 64 : 25 : 49
d) 49 : 25 : 64
Answer
Correct Answer: (c) 64 : 25 : 49
Solution
A⁄3 = B⁄2 = C⁄5 = k (say)
∴ A = 3k, B = 2k and C = 5k
Now, putting these values in (C + A)2 : (A + B)2 : (B + C)2, we have,
= (5k + 3k)2 : (3k + 2k)2 : (2k + 5k)2
= 64k2 : 25k2 : 49k2
= 64 : 25 : 49 (Ans.)
Q.6) 5 years ago the average age of a family which includes father, mother and a son was 35 years. 3 years ago the average age of father and mother was 46 years. What is the present age (in years) of the son ?
a) 20
b) 24
c) 26
d) 22
Answer
Correct Answer: (d) 22
Solution
Shortcut Approach :
Average present age (means 5 years after from 5 years ago) of 3 members (i.e. father, mother and son)
= 35 + (5 × 3)⁄3 = 40 years.
Average present age (means 3 years after from 3 years ago) of 2 members (i.e. father and mother )
= 46 + (3 × 2)⁄2 = 49 years.
∴ Present age of Son = [Total age of 3 members (father, mother and son) − Total age of 2 members (father and mother)]
= 40 × 5 − 49 × 2 = 22 years. (Ans.)
Q.7) The cost price of 60 articles is same as the selling price of x articles. If there is a profit of 20%, then what is the value of x ?
a) 15
b) 30
c) 50
d) 80
Answer
Correct Answer: (c) 50
Solution
Let, C.P. of 60 articles = S.P. of x no. articles = y
Therefore, C.P. of x articles = xy⁄60
Profit = S.P. – C.P. = y − xy⁄60 = (60y − xy)⁄60
Profit percentage = Profit⁄C.P. × 100 %
( 60y−xy 60 ) ( xy 60 ) ×100% = 60y−xy xy ×100% =( 60 x −1 )×100%
Now, according to the statement of the question given, we have
( 60 x −1 )×100%=20% ⇒ 60 x −1= 20 100 ⇒ 60 x = 1 5 +1= 6 5 ∴x=50 ……………(Ans.)
Q.8) A person scores 45% of the total marks in the exam and still fails by 40 marks. The passing percentage of the exam is 55%. What is the maximum marks of the exam ?
a) 300
b) 350
c) 400
d) 500
Answer
Correct Answer: (c) 400
Solution
Shortcut Approach:
Let, total marks of the exam be 100
A person scores = 45 % of total marks means he/she scores = 45 marks when the total marks are 100.
But passing marks = 55 % of total marks.
Therefore, pass mark = 55 when total marks are 100.
Hence, he/she fail by = 55 − 45 = 10 marks.
Now, we can say,
A person fails by 10 marks when the total marks 100
∴ A person fails by 40 marks when the total marks = 100⁄10 × 40 = 400 (Ans.)
Q.9) A man starts running from point P at 11:00 a.m. with a speed of 10 km/hr. He runs for 2 hours and then takes a 1 hour rest. He continues this till he is caught by another man who starts at 2:00 p.m. from point P and runs non-stop at a speed of 15 km/hr towards the first man. At what time (in p.m.) will the first man be caught ?
a) 6:20
b) 4:40
c) 6:00
d) 5:30
Answer
Correct Answer: (b) 4:40
Solution
We know, the speed of the first man = 10 km/hr
According to the statement of the question, the first man runs for 2 hours and then take rest.
Therefore, distance covered by him in 3 hours = 2 × 10 = 20 km
So, we can say, at 2 p.m. (11:00 a.m. + 3 hours) 1st man will be 20 km far from point P and the second man will be at point P.
Now, in next 2 hours means at 4 p.m., distance covered by first man = 20 km and he will not move for another 1 hour.
As, the speed of the 2nd man = 15 km/hr
Therefore, from 2 p.m. to 4 p.m. means in 2 hours, distance covered by second man = 2 × 15 = 30 km and still 10 km (= 40 − 30) left to meet 1st man.
Time required to cover 10 km by second man = 10⁄15 hour = 40 minutes.
Therefore, at 4:40 p.m. the first man will be caught. (Ans.)
Q.10) The difference of compound interest and simple interest for 3 years and for 2 years are in ratio 23 : 7 respectively. What is rate of interest per annum (in %) ?
a) 200⁄7
b) 100⁄7
c) 300⁄7
d) 400⁄7
Answer
Correct Answer: (a) 200⁄7
Solution
Let, Principal = P and rate of interest = r %
C.I. of 2 years,
=P (1+ r 100 ) 2 −P =P(1+ 2r 100 + r 2 10000 )−P =P( 1 + 2r 100 + r 2 10000 − 1 ) =P( 2r 100 + r 2 10000 ) = 2Pr 100 + Pr 2 10000
S.I. of 2 years = 2Pr⁄100
Difference of C.I. and S.I. for 2 years,
=C.I.−S.I. =( 2Pr 100 + Pr 2 10000 )− 2Pr 100 = Pr 2 10000
C.I. of 3 years,
=P (1+ r 100 ) 3 −P =P(1+ 3 r 2 10000 + 3r 100 + r 3 1000000 )−P =P( 1 + 3 r 2 10000 + 3r 100 + r 3 1000000 − 1 ) =P( 3 r 2 10000 + 3r 100 + r 3 1000000 ) = 3P r 2 10000 + 3Pr 100 + P r 3 1000000
S.I. of 3 years = 3Pr⁄100
Difference of C.I. and S.I. for 3 years,
=C.I.−S.I. =( 3P r 2 10000 + 3Pr 100 + P r 3 1000000 )− 3Pr 100 =( 3P r 2 10000 + P r 3 1000000 ) = Pr 2 10000 ( 3+ r 100 )
According to the statement of the problem, we have
⇒ Pr 2 10000 ( 3+ r 100 ): Pr 2 10000 =23:7 ⇒( 3+ r 100 )= 23 7 ⇒ r 100 = 23 7 −3 ⇒ r 100 = 2 7 ∴r= 200 7 ……….(Ans.)
Q.11) If x2⁄yz + y2⁄zx + z2⁄xy = 3, then what is the value of (x + y + z)3 ?
a) 0
b) 1
c) 2
d) 3
Answer
Correct Answer: (a) 0
Solution
As, x2⁄yz + y2⁄zx + z2⁄xy = 3
Therefore,
⇒ x 3 + y 3 + z 3 xyz =3 ⇒ x 3 + y 3 + z 3 =3xyz ∴ x 3 + y 3 + z 3 −3xyz=0
Now we know that x3 + y3 + z3 − 3xyz = (x + y + z)(x2 + y2 + z2 – xy – yz – zx)
If x + y + z = 0 then x3 + y3 + z3 − 3xyz = 0
∴ The value of required (x + y + z)3 = 0 (Ans.)
Q.12) If x1⁄4 + x– 1⁄4 = 2, then what is the value of x81 + 1⁄x81 ?
a) − 2
b) 0
c) 1
d) 2
Answer
Correct Answer: (d) 2
Solution
Note: If x + 1⁄x = 2 , then x = 1 and also 1⁄x = 1
Therefore, x1⁄4 + x– 1⁄4 = 2 for x1⁄4 = 1 and x– 1⁄4 =1
Hence, x = 1
Now, x81 + 1⁄x81 = (1)81 + 1⁄(1)81 = 1 + 1 = 2 (Ans.)
Q.13) If a(a + b + c) = 45, b(a + b + c) = 75 and c(a + b + c) = 105, then what is the value of (a2 + b2 + c2) ?
a) 75
b) 83
c) 217
d) 225
Answer
Correct Answer: (b) 83
Solution
a(a + b + c) + b(a + b + c) + c(a + b + c) = 45 + 75 + 105 = 225
or, a2 + ab + ac + ab + b2 + bc + ac + bc + c2 = 225
or, a2 + b2 + c2 + 2ab + 2bc + 2ca = 225
or, (a + b + c)2 = (15)2
∴ a + b + c = 15
Now, a(a + b + c) = 45, ⇒ a × 15 = 45, ⇒ a = 3
Similarly, b = 5 and c = 7
Now, a2 + b2 + c2
= 32 + 52 + 72
= 83 (Ans.)
Q.14) If x2 + 1⁄x2 = 1, then what is the value of x48 + x42 + x36 + x30 + x24 + x18 + x12 + x6 + 1 ?
a) − 9
b) 0
c) 1
d) 9
Answer
Correct Answer: (c) 1
Solution
Given, x2 + 1⁄x2 = 1
Therefore,
x 4 +1= x 2 ………..(i) x 6 + x 2 = x 4 ………(ii) [multiplying by x 2 both side] Now, adding eq n (i) and (ii), we have, x 6 +1=0 Now, x 48 + x 42 + x 36 + x 30 + x 24 + x 18 + x 12 + x 6 +1 = x 42 ( x 6 +1 )+ x 30 ( x 6 +1 )+ x 18 ( x 6 +1 )+ x 6 ( x 6 +1 )+1 = x 42 ( 0 )+ x 30 ( 0 )+ x 18 ( 0 )+ x 6 ( 0 )+1 =1 ………..(Ans.)
Q.15) In the given figure PQRS is a trapezium in which PM ∥ SN, NR = 9 cm, PS = 12 cm, QM = NR and NR = SN. What is the area (in sq.cm.) of trapezium ?

a) 170 sq.cm.
b) 182 sq.cm
c) 189 sq.cm
d) 191 sq.cm
Answer
Correct Answer: (c) 189 sq.cm.
Solution
We know that, area of a trapezium = 1⁄2 × (sum of parallel sides) × distance between two parallel sides
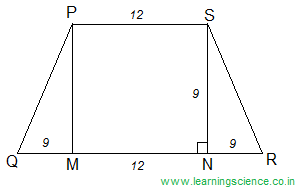
∴ Area of trapezium PQRS = 1⁄2 × (PS + QR) × SN
= 1⁄2 × (12 + 30) × 9
= 189 sq cm. (Ans.)
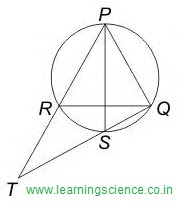
Q.16) In the given figure, PQR is an equilateral triangle and PS is the angle bisector of ∠ P. What is the value of RT : RQ ?
a) 1 : 2
b) 1 : 1
c) 2 : 1
d) 1 : 3
Answer
Correct Answer: (b) 1 : 1
Solution
∆ PQR is an equilateral triangle and PS is a bisector of ∠ RPQ.
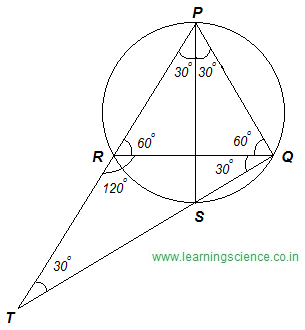
∴ ∠ PRQ = ∠RQP = ∠RPQ = 60° and ∠RPS = ∠QPS = 30°
Again, as ∠RPS and ∠ ∠ RQS are lie in the same segment of the same circle.
∴ ∠ RPS = ∠RQS = 30°
∠TRQ = 180° − ∠PRQ = 180° − 60° = 120°
In ∆ RTQ, we have,
∠RTQ + ∠TQR + ∠TRQ = 180° [Applying angle sum property of triangle]
∠RTQ + 120° + 30° = 180°
∴ ∠ RTQ = 180° − 150° = 30°
∴ we can say ∆ RTQ is an isosceles triangle whose RQ = RT
∴ RT : RQ = 1 : 1 (Ans.)
Q.17) Two chords of length 20 cm and 24 cm are drawn perpendicular to each other in a circle of radius is 15 cm. What is the distance between the Points of intersection of these chords (in cm) from the center of the circle ?
a) √114
b) √182
c) √206
d) √118
Answer
Correct Answer: (c) √206
Solution
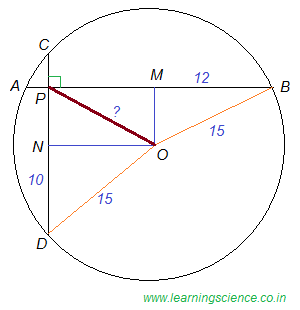
Let, AB and CD are two chords intersects perpendicularly at point P and ‘O’ be the centre of the given circle.
Therefore, we have to find OP =?
Taking AB = 24 cm and CD = 20 cm.
Given, radius of the circle, OB = OD = 15 cm.
Now, perpendicular OM and ON are drawn from point O on the chord AB and CD respectively.
Therefore, BM = 24⁄2 = 12 cm and DN = 20⁄2 = 10 cm.
In, right-angled triangle OBM, we have,
OM2 = OB2 − BM2
= 152 − 122
= 81
∴ OM2 = 81 = PN2 [since, OMPN is a rectangle]
Similarly, from right-angled triangle ODN,
ON2 = 152 − 102
= 125
∴ ON2 = 125
Now, in right-angled triangle OPN,
OP2 = PN2 + ON2
= 81 + 125
= 206
∴ OP = √206 (Ans.)
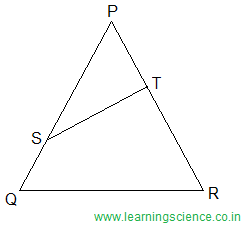
Q.18) In the given figure, QRTS is a cyclic quadrilateral. If PT = 5 cm, SQ = 4 cm, PS = 6 cm and ∠ PQR = 63°, then what is the value (in cm.) of TR ?
a) 3
b) 7
c) 9
d) 15
Answer
Correct Answer: (b) 7
Solution
Given, QRTS is a cyclic quadrilateral.
Therefore, we can say ∠SQR = ∠PTS and ∠PST = ∠TRQ
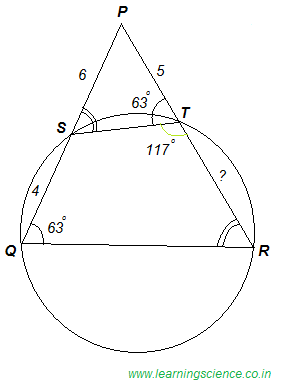
∵ In ∆PST and ∆PQR
∠PTS = ∠PQR
∠PST = ∠PRQ
and remaining ∠SPT = remaining ∠QPR [common angle]
∴ ∆PST and ∆PQR are similar
Hence, we can write PS⁄PR = PT⁄PQ
⇒ 6⁄(5 + TR) = 5⁄(6 + 4)
⇒ 6⁄(5 + TR) = 5⁄10 = 1⁄2
⇒ 5 + TR = 12
∴ TR = 7 cm. (Ans.)
Q.19) What is the simplified value of sin2(90 − θ) − {sin(90 − θ)sin θ}⁄tan θ ?
a) 1
b) cosec θ
c) 0
d) cos θ
Answer
Correct Answer: (c) 0
Solution
The simplified value is as follows,
sin 2 ( 90−θ )− sin( 90−θ )sinθ tanθ = cos 2 θ− cosθ⋅sinθ tanθ = cos 2 θ− cosθ⋅ sinθ ( sinθ cosθ ) = cos 2 θ− cos 2 θ =0 ………….(Ans.)
Q.20) What is the simplified value of
[ cos 2 θ 1+sinθ − sin 2 θ 1+cosθ ] 2
a) sin θ
b) 1 − sin 2θ
c) 1 + sin 2θ
d) 1 − sin θ
Answer
Correct Answer: (b) 1 − sin 2θ
Solution
The simplified value is as follows,
[ cos 2 θ 1+sinθ − sin 2 θ 1+cosθ ] 2 = [ 1− sin 2 θ 1+sinθ − 1− cos 2 θ 1+cosθ ] 2 = [ ( 1+sinθ ) ( 1−sinθ ) ( 1+sinθ ) − ( 1+cosθ ) ( 1−cosθ ) ( 1+cosθ ) ] 2 = ( 1 −sinθ− 1 +cosθ ) 2 = ( cosθ−sinθ ) 2 = cos 2 θ+ sin 2 θ−2sinθ⋅cosθ =1−2sinθ⋅cosθ =1−sin2θ [since, 2sinθ⋅cosθ=sin2θ] ……(Ans.)Shortcut Approach:
If you consider the value of θ = 45°
Then the numerical value of required trigonometric function = 0 and option ‘b’ i.e. 1 − sin 2θ is also 0
Therefore, the right option is ‘b’
Q.21) If 5 sec θ − 3 tan θ = 5, then what is the value of 5 tan θ − 3 sec θ ?
a) 1
b) 2
c) 3
d) 4
Answer
Correct Answer: (c) 3
Solution
Here, 5 sec θ − 3 tan θ = 5
or, 5 sec θ = 5 + 3 tan θ
or,(5 sec θ)2 = (5 + 3 tan θ)2 [squiring both sides]
or, 25 sec2θ = 25 + 9 tan2θ + 30 tan θ
or, 25 (1 + tan2θ) = 25 + 9 tan2θ + 30 tan θ
or, 25 + 25 tan2θ − 25 − 9 tan2θ − 30 tan θ = 0
or, 16 tan2θ − 30 tan θ = 0
or, 2 tan θ (8 tan θ − 15)= 0
Therefore,
either, 2 tan θ = 0 ⇒ tan θ = 0 and hence, sec θ = 1
or, 8 tanθ − 15= 0
⇒ tanθ = 15⁄8 and hence, sec θ = 17⁄8
Now, if we consider, tan θ = 0 and sec θ = 1, then the required 5 tan θ − 3 sec θ = − 3 (there has no such option in the given question)
But, if we consider, tanθ = 15⁄8 and sec θ = 17⁄8 , then the required 5 tan θ − 3 sec θ ⇒ 5 × 15⁄8 − 3 × 17⁄8 = 3 (option ‘c’) (Ans.)
Q.22) The table below shows the distribution of number of people living in 8 different countries and per capita income of each of the countries. The total population of these countries taken together is 200 crores.
Per capita income = Total GDP of country/population of the country.
What is the difference (in crores) in population of the most and the least populated country ?
a) 18
b) 32
c) 34
d) 36
Answer
Correct Answer: (d) 36
Solution
Given, total population of all countries = 200 crores.
We can see from the adjoining table that the country 4 has got maximum population (i.e. 24 % of the total) while country 6 has got minimum population (i.e. 6 % of the total)
Therefore, the required difference in population of the most and the least populated country,
= (24 − 6)⁄100 × 200 crores
= 36 crores (Ans.)
Q.23) The table below shows the distribution of number of people living in 8 different countries and per capita income of each of the countries. The total population of these countries taken together is 200 crores.
Per capita income = Total GDP of country/population of the country.
What is the total GDP (in crore dollars) of country 5 ?
a) 27120
b) 31640
c) 38280
d) 44660
Answer
Correct Answer: (b) 31640
Solution
As, the total GDP of country = (Per capita income of the country) × (Population of the country)
Therefore, total GDP of Country 5 = 2260 × ( 7⁄100 × 200 ) crore dollars
= 31640 crore dollars. (Ans.)
Q.24) The table below shows the distribution of number of people living in 8 different countries and per capita income of each of the countries. The total population of these countries taken together is 200 crores.
Per capita income = Total GDP of country/population of the country.
What is the total GDP (in crore dollars) for the country with the third lowest per capita income ?
a) 181900
b) 108460
c) 145200
d) 164560
Answer
Correct Answer: (d) 164560
Solution
We can see from the adjoining table that the Country 4 has got the third lowest per capita income.
As, the total GDP of country = (Per capita income of the country) × (Population of the country)
Therefore, total GDP of Country 4 = 4840 × ( 17⁄100 × 200 ) crore dollars
= 164560 crore dollars. (Ans.)
Q.25) The table below shows the distribution of number of people living in 8 different countries and per capita income of each of the countries. The total population of these countries taken together is 200 crores.
Per capita income = Total GDP of country/population of the country.
Which country has the highest total GDP ?
a) Country 1
b) Country 2
c) Country 3
d) Country 8
Answer
Correct Answer: (c) Country 3
Solution
As, the total GDP of country = (Per capita income of the country) × (Population of the country)
Therefore,
Total GDP of Country 1 = 11850 × ( 12⁄100 × 200 ) crore dollars
= 2,84,400 crore dollars.
Total GDP of Country 2 = 5350 × ( 24⁄100 × 200 ) crore dollars
= 2,56,800 crore dollars.
Total GDP of Country 3 = 9900 × ( 15⁄100 × 200 ) crore dollars
= 2,97,000 crore dollars.
Total GDP of Country 4 = 4840 × ( 17⁄100 × 200 ) crore dollars
= 1,64,560 crore dollars.
Total GDP of Country 5 = 2260 × ( 7⁄100 × 200 ) crore dollars
= 31,640 crore dollars.
Total GDP of Country 6 = 6920 × ( 6⁄100 × 200 ) crore dollars
= 83,040 crore dollars.
Total GDP of Country 7 = 3190 × ( 11⁄100 × 200 ) crore dollars
= 70,180 crore dollars.
Total GDP of Country 8 = 10410 × ( 8⁄100 × 200 ) crore dollars
= 1,66,560 crore dollars.
Hence, the required country which has got the most total GDP is Country 3. (Ans.)
If you still have any query then feel free to contact or comment below. I will definitely try to solve your issue. Thank you.