SSC CGL Held on 8th August 2017 Shift 1

SSC CGL Held on 8th August 2017 Shift 1
Staff Selection Commission – Combined Graduate Level Examination, often referred to as SSC CGL is an examination conducted to recruit staff to various posts in ministries, departments and organisations of the Government of India. It is conducted by the Staff Selection Commission for selecting staff for various Group B and Group C posts. The Staff Selection Commission was established in 1975.
Candidates applying for the various posts need to have a bachelor’s degree from a recognised university at the time of applying. Age of the candidate must be between 18 and 32 years (depending upon post applied).
For more click here.
Q.1) How many numbers are there from 300 to 650 which are completely divisible by both 5 and 7 ?
a) 8
b) 9
c) 10
d) 12
Answer
Correct Answer: (c) 10
Solution
Soln
The LCM of 5 and 7 is 35.
300⁄35 = 8.57 (approx.), (don’t need to divide it upto decimal value.)
∴ 9 × 35 = 315 which is smallest number divisible by both 5 and 7.
650⁄35 = 18.57,
∴ 18 × 35 = 630 which is largest number divisible by both 5 and 7.
Add the digits 9, 10,…….,17 & 18. We got 10 numbers.
Answer: There are 10 numbers between 300 and 650 which are divisible by both 5 and 7.
Q.2) Raman can do a work in 5 days, Jatin can do the same work in 7 days and Sachin can do the same work in 9 days. If they do the same work together and they are paid Rs 2860, then what is the share (in Rs) of Raman ?
a) 1260
b) 700
c) 900
d) 870
Answer
Correct Answer: (a) 1260
Solution
Soln
Shortcut Method:
L.C.M. of 5, 7 and 9 = 315
Raman works = 315⁄5 = 63 units
Jatin works = 315⁄7 = 45 units and
Sachin works = 315⁄9 = 35 units.
If they worked together, then total work = (63 + 45 + 35) = 143 units
According to the problem, we have
143 units = Rs. 2860
∴ 63 units = Rs. (2860 × 63)⁄143 = Rs. 1260 ………(Ans.)
Q.3) If the diameter of a sphere is 14 cm, then what is the surface area (in cm2) of the sphere ?
a) 616
b) 308
c) 462
d) 636
Answer
Correct Answer: (a) 616
Solution
Radius of the sphere (r) = 14⁄2 = 7 cm.
∴ Surface area = 4πr2
= 4 × 22⁄7 × 72
= 4 × 22 × 7
= 616 sq. cm. ……….(Ans.)
Q.4) After two successive discounts of 20% and 35%, an article is sold for Rs 50700. What is the marked price (in Rs) of the article ?
a) 92500
b) 98500
c) 97500
d) 94500
Answer
Correct Answer: (c) 97500
Solution
Shortcut Method:
If x be the 1st discount and y be the 2nd discount, then we have
Total successive discount =
( x+y− x×y 100 )%
In this problem, x = 20 and y = 35
∴ Total discount =
( 20+35− 20×35 100 )%
= 48 %
Given, Selling Price (S.P.) of an article = Rs. 50700
∴ Market Price (M.P.) = Rs.100⁄(100 − 48)
= Rs.100⁄52 × 50700
= Rs. 97500 …………….(Ans.)
Q.5) Rs 3200 is divided among A, B and C in the ratio of 3 : 5 : 8 respectively. What is the difference (in Rs) between the share of B and C ?
a) 400
b) 600
c) 800
d) 900
Answer
Correct Answer: (b) 600
Solution
Shortcut Method:
Ratio of shares of A, B and C = 3 : 5 : 8
Sum of ratio = 3 + 5 + 8 = 16
Difference in ratio of B and C out of 16 = 8 – 5 = 3
Total amount = Rs. 3200
∴ Difference of shares between B and C = Rs.3⁄16 × 3200
= Rs. 3 × 200
= Rs. 600 ……………..(Ans.)
Q.6) The average of 5 members of a family is 24 years. If the youngest member is 8 years old, then what was the average age (in years) of the family at the time of the birth of the youngest member ?
a) 16
b) 20
c) 24
d) 32
Answer
Correct Answer: (b) 20
Solution
The average age of 5 members = 5 × 24 = 120 years
The age of the youngest member = 8 years.
But, as per the statement of the question given, time of the birth of the youngest member means 8 years ago.
Hence, before 8 years their (4 members) total ages = 120 – 5 × 8 = 80 years.
∴ Average age of the family = 80⁄4 years
= 20 years. ……………..(Ans.)
Q.7) If the price of pen decreases by 20%, then a man can buy 10 more pens for Rs 100. What is the new price (in Rs) of each pen ?
a) 1
b) 2
c) 3
d) 4
Answer
Correct Answer: (b) 2
Solution
Let, initial price of each pen = x and total no. of pen (in Rs.100) = y
∴ Total price of x no. of pens = xy
Given, xy = Rs. 100
Hence, y = 100⁄x
After decreasing the price of pen, new price of each pen,
= Rs.x × (100 − 20)⁄100
= Rs.4x⁄5
Number of pen that he can buy in Rs. 100, we have
= 100 ÷ 4x⁄5
= 125⁄x
Now, we have,
⇒ 125⁄x − y = 10
⇒ 125⁄x − 100⁄x = 10
∴ x = Rs. 2.5
∴ New price = Rs.4x⁄5
= Rs. (4 × 2.5)⁄5
= Rs. 2 ……………………(Ans.)
Q.8) After deducting 60% from a certain number and then deducting 15% from the remainder, 1428 is left. What was the initial number ?
a) 4200
b) 3962
c) 4150
d) 4300
Answer
Correct Answer: (a) 4200
Solution
Shortcut Method:
Let, the actual number be y
∴ After two successive deduction of 60 % and 15 %, the number we have left 1428.
∴ We can write,
⇒ (100 − 60)⁄100 × (100 − 15)⁄100 × y = 1428
∴ y = 4200 ……………………(Ans.)
Q.9) A train travels 40% faster than a car. Both start from point A at the same time and reach point B, 140 km away at the same time. On the way the train takes 25 minutes for stopping at the stations. What is the speed (in km/hr) of the train ?
a) 67
b) 134.4
c) 145.9
d) 160
Answer
Correct Answer: (b) 134.4
Solution
Let, speed of the car = x km/hr
∴ Speed of the train = x × (100 + 40)⁄100 km/hr
= 7x⁄8 km/hr
Now, according to the question given, we have
Tcar – Ttrain = 25 minutes
⇒ 140 V car − 140 V train = 25 60 hours ⇒ 140 x − 140 ( 7x 5 ) = 25 60 ⇒ 140 x ( 1− 5 7 )= 25 60 ⇒ 140 x × 2 7 = 25 60 ⇒x= 60 25 × 2 7 ×140
∴ x = 96 hour
Hence, Speed of the train = 7x⁄5 km/hr
= (7 × 96)⁄5 = 134.4 km/hr ……………..(Ans.)
Q.10) A certain sum of money triples itself in 5 years at simple interest. In how many years it will be five times ?
a) 5
b) 8
c) 10
d) 15
Answer
Correct Answer: (c) 10
Solution
Let, principle (P) = x
∴ Amount (A) = 3x
Hence, Interest (I) = 3x − x = 2x
Time (t) = 5 years.
∴ Rate of interest (r) = (100 × I)⁄(P × t)
r = (100 × 2x)⁄(x × 5) = 40 %
Now, again, A = 5x
∴ I = 5x − x = 4x
r = 40 %
t = ?
∴ t = (100 × I)⁄(P × r)
t = (100 × 4x)⁄(x × 40) = 10 years. ……………………….(Ans.)
Q.11) If
x+1x=2
, then what is the value of x64 + x121 ?
a) 0
b) 1
c) 2
d) – 2
Answer
Correct Answer: (c) 2
Solution
Shortcut Method:
If x + 1⁄x = 2 , then x = 1
∴ x64 + x121 = (1)64 + (1)121 = 1 + 1 = 2 ………………..(Ans.)
Q.12) If
x=6+26
, then what is the value of
x-1+1x-1
?
a) 2√3
b) 3√2
c) 2√2
d) 3√3
Answer
Correct Answer: (a) 2√3
Solution
x = 6 + 2√6
∴ x − 1 = 5 + 2√6
= (√3)2 + (√2)2 + 2 x √3 x √2
= (√3 + √2)2
Hence, √(x − 1)= (√3 + √2) (taking +ve value, since x is greater than 1)
As, we have seen that (√3)2 − (√2)2 = 1
∴ The value of 1⁄√(x − 1) should be = (√3 − √2)
∴ √(x − 1) + 1⁄√(x − 1) = (√3 + √2) + (√3 − √2) = 2√3 ……………………(Ans.)
Q.13) If a + b + c = 27, then what is the value of (a – 7)3 + (b – 9)3 + (c – 11)3 – 3(a – 7)(b – 9)(c – 11) ?
a) 0
b) 9
c) 27
d) 81
Answer
Correct Answer: (a) 0
Solution
Let, (a – 7) = x, (b – 9) = y and (c – 11) = z
∴ x + y + z = (a – 7) + (b – 9) + (c – 11) = (a + b + c) – 27 = 27 – 27 = 0
We know that if x + y + z = 0, then
x3 + y3 + z3 – 3xyz = 0
∴ (a – 7)3 + (b – 9)3 + (c – 11)3 – 3(a – 7)(b – 9)(c – 11) = 0 ……….(Ans.)
Q.14) If
x=2153+5
, then what is the value of
x+5x-5+x+3x-3
?
a) √5
b) √3
c) √15
d) 2
Answer
Correct Answer: (d) 2
Solution
Note: If the value of x has given in such way that,
x = 2ab⁄(a + b) and the required question has asked in such way that (x + a)⁄(x − a) + (x + b)⁄(x − b) = ?
Then the required value of (x + a)⁄(x − a) + (x + b)⁄(x − b) should be = 2
In this problem, if you assume a = √5 and b = √3, then we can write the sum like that
x = 2√15⁄(√5 + √3) = 2√5 × √3⁄(√5 + √3)
∴ (x + √5)⁄(x − √5) + (x + √3)⁄(x − √3) = 2 …………..(Ans.)
Detailed Process:
x= 2 15 5 + 3 ⇒x= 2 5 ⋅ 3 5 + 3 ⇒ x 5 = 2 3 5 + 3 ⇒ x+ 5 x− 5 = 2 3 +( 5 + 3 ) 2 3 −( 5 + 3 ) ⇒ x+ 5 x− 5 = 2 3 + 5 + 3 2 3 − 5 − 3 ∴ x+ 5 x− 5 = 3 3 + 5 3 − 5
Similarly,
x+ 3 x− 3 = 3 5 + 3 5 − 3
Now L.H.S.,
x+ 5 x− 5 + x+ 3 x− 3 ⇒ 3 3 + 5 3 − 5 + 3 5 + 3 5 − 3 ⇒ 3 3 + 5 3 − 5 − 3 5 + 3 3 − 5 ⇒ 3 3 + 5 −3 5 − 3 ( 3 − 5 ) ⇒ 2 3 −2 5 ( 3 − 5 ) ⇒ 2( 3 − 5 ) ( 3 − 5 ) =2
Q.15) The perimeter of an isosceles triangle is 32 cm and each of the equal sides is 5/6 times of the base. What is the area (in cm2) of the triangle ?
a) 39
b) 48
c) 57
d) 64
Answer
Correct Answer: (b) 48
Solution
Let, Length of base = b
∴ Length of each equal side (a) = 5b⁄6

∴ We have,
Perimeter = 32 cm
∴ 2a + b = 32
or, 2 × 5b⁄6 + b = 32
∴ b = 12 cm and
a = 5b⁄6 = (5 × 12)⁄6 = 10 cm.
Height (h) = √[a2 − ( b⁄2 )2]
= √[102 − ( 12⁄2 )2]
= √[100− 36]
= 8 cm.
We know that, area of an isosceles triangle,
= ½ × b × h sq.cm.
= ½ x 12 x 8 sq.cm.
= 48 sq.cm …………………(Ans.)
Q.16) If length of each side of a rhombus PQRS is 8 cm and ∠PQR = 120°, then what is the length (in cm) of QS ?
a) 4√5
b) 6
c) 8
d) 12
Answer
Correct Answer: (c) 8
Solution
As we know that diagonal of a rhombus bisects its angle.

Here, ∠ PQR = 120°
Line QS is one diagonal which bisects ∠ PQR.
∴ ∠ PQS = 60°
As, PQ = PS = 8 cm.
Therefore, ∠ PSQ = 60°
Hence, remaining ∠ QPS = 60°
∴ ∆ PQS is an equilateral triangle.
∴ The required length of side QS = 8 cm. ……………………….(Ans.)
Q.17) In the given figure, ABC is a triangle. The bisectors of internal ∠ B and external ∠ C intersects at D. If ∠ BDC = 48°, then what is the value (in degrees) of ∠ A ?

a) 48
b) 96
c) 100
d) 114
Answer
Correct Answer: (b) 96
Solution

In ∆ BCD, external ∠ DCE = internal (∠ CBD + ∠ BDC)
∴ x = 48° + y
Again, In ∆ BCD,
External ∠ ACE = internal (∠ CBA + ∠ A)
∴ x + x = y + y + ∠ A
or, 2x = 2y + ∠ A
or, ∠ A = 2y – 2x
or, ∠ A = 2y – 2(48° + y)
∴ ∠ A = 96° …………………..(Ans.)
Q.18) In the given figure, O is the centre of the circle and ∠ DCE = 45°. If CB = BD and CD = 10√2 cm, then what is the length (in cm) of AC ?

a) 14
b) 15.5
c) 18.5
d) 20
Answer
Correct Answer: (c) 18.5
Solution
Note: The length of the AC can’t be determined if it is not state that ∠ OCE = 90°
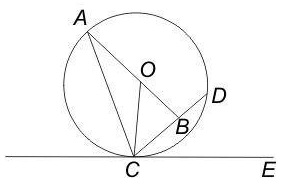
Now, we have ∠ DCE = 45°
∴ ∠ OCB = 45°
Hence, we can say ∆OBC is a right-angled isosceles triangle means BC = OB = 10√2/2 cm = 5√2 cm.
In right-angled isosceles triangle OBC, we have,
OC2 = BO2 + BC2 [using ‘Pythagoras theorem’]
⇒ OC2 = (5√2)2 + (5√2)2
∴ OC2 = 100 ⇒ OC = 10 cm.
∴ OC = AB = 10 [ OC = AB, radius of same circle ]
Now, In right-angled ∆ ABC, we have
AC2 = BC2 + AB2
⇒ AC2 = (5√2)2 + (OB + AO)2
⇒ AC2 = (5√2)2 + (5√2 + 10)2
⇒ AC2 = 50 + 50 + 2 x 5√2 x 10 + 100
∴ AC = √341.42 = 18.5 cm. (approx.) ………………….(Ans.)
Q.19) What is the simplified value of
sin2A1+cos2A
?
a) tan A
b) cot A
c) sin A
d) cos A
Answer
Correct Answer: (a) tan A
Solution
We know that 1 + cos 2A = 2cos2 A and sin2 A = 2sin A.cos A
∴ sin 2A⁄(1 +cos 2A) = 2 sin A.cos A⁄2 cos2 A = tanA ……………..(Ans.)
Q.20) What is the simplified value of
secAtanA+cotA2
?
a) 1 – cos2A
b) 2sin2A
c) sec2A
d) cosec2A
Answer
Correct Answer: (a) 1 – cos2A
Solution
Shortcut Method:
Let A = 45°
Then sec A = sec 45° = √2
tan A + cot A = tan 45° + cot 45° = 1 + 1 = 2
Now
( secA tanA+cotA ) 2 ⇒ ( 2 2 ) 2 = 1 2 ⇒1− cos 2 A=1− cos 2 45 o = 1 2
Detailed Procss:
(secAtanA+cotA)2⇒(1cosAsinAcosA+cosAsinA)2⇒(1cosA×sinA×cosAsin2A+cos2A)2⇒sin2A=1−cos2A
Q.21) What is the simplified value of 1 + tan A tan (A/2) ?
a) sin A/2
b) cos A
c) sec A
d) sin A
Answer
Correct Answer: (c) sec A
Solution
Shortcut Method:
Let A = 60°
∴ 1 + tan A × tan ( A⁄2 ) = 1 + tan 60° × tan 30°
⇒ 1 + √3 × 1⁄√3 = 2 = sec2 A = sec2 60° = 2
Detailed Procss:
1+tanA×tan(A/2)=1+2tan(A/2)1−tan2(A/2)×tan(A/2)=1+2tan2(A/2)1−tan2(A/2)=1−tan2(A/2)+2tan2A1−tan2(A/2)=1+tan2(A/2)1−tan2(A/2)=sec2A
Q.22) The ‘Pie Chart’ given below shows the number of shoes of five different brands in a multi brand store. There are total 1200 shoes.

How many shoes are there of Reebok brand ?
a) 230
b) 276
c) 286
d) 216
Answer
Correct Answer: (b) 276
Solution

Total number of shoes = 1200 on which Reebok shoe = 23 %
∴ Number of Reebok shoes = 1200 × 23⁄100 = 276 ……………(Ans.)
Q.23) The ‘Pie Chart’ given below shows the number of shoes of five different brands in a multi brand store. There are total 1200 shoes.

What is the difference in number of shoes of Puma and Vans ?
a) 96
b) 156
c) 84
d) 112
Answer
Correct Answer: (a) 96
Solution

Total number of shoes = 1200
Percentage of Puma shoe = 21 % and Vans = 13 %
Difference in percentage = 21 – 13 = 8 %
∴ Difference in number of Puma and Vans shoes = 1200 × 8⁄100 = 96 ………(Ans.)
Q.24) The ‘Pie Chart’ given below shows the number of shoes of five different brands in a multi brand store. There are total 1200 shoes.

The difference between the number of shoes of Reebok and Nike is same as the difference between which of the following two brands ?
a) Puma and Adidas
b) Reebok and Adidas
c) Vans and Nike
d) Nike and Adidas
Answer
Correct Answer: (c) Vans and Nike
Solution

From the adjoining figure, we have clearly seen that the difference in the percentage of Reebok and Nike is 5 % and we also see that the difference in percentage is same means 5 % for Nike and Vans.
∴ Answer will be Nike and Vans. ……………………..(Ans.)
Q.25) The ‘Pie Chart’ given below shows the number of shoes of five different brands in a multi brand store. There are total 1200 shoes.

Puma shoes are how much percent more than the Nike Shoes ?
a) 14.28
b) 16.66
c) 25
d) 21.33
Answer
Correct Answer: (b) 16.66
Solution

The number of Nike shoes = 1200 × 18⁄100 = 216
The number of Puma shoes = 1200 × 21⁄100 = 252
∴ The number of excess shoes of Puma than Nike = 252 – 216 = 36
∴ in percentage = 36⁄216 × 100 % = 16.66 % (approx.) ……………….(Ans.)
If you still have any query then feel free to contact or comment below. I will definitely try to solve your issue. Thank you.
SSC CGL Held on 8th August 2017 Shift 1,