SSC CGL Held on 9th August 2017 Shift 1

SSC CGL Held on 9th August 2017 Shift 1
Staff Selection Commission – Combined Graduate Level Examination, often referred to as SSC CGL is an examination conducted to recruit staff to various posts in ministries, departments and organisations of the Government of India. It is conducted by the Staff Selection Commission for selecting staff for various Group B and Group C posts. The Staff Selection Commission was established in 1975.
Candidates applying for the various posts need to have a bachelor’s degree from a recognised university at the time of applying. Age of the candidate must be between 18 and 32 years (depending upon post applied).
For more click here.
Q.1)
Which value among 5 3 , 6 4 , 12 6 , 276 12 is the largest ?
a) 53
b) 64
c) 126
d) 27612
Answer
Correct Answer: (a) ∛5
Solution
Q.2) A piece of work was finished by A, B and C together. A and B together finished 60% of the work and B and C together finished 70% of the work. Who among the three is most efficient ?
a) A
b) B
c) C
d) A or B
Answer
Correct Answer: (c) C
Solution
Let, the total work be 100 % which was finished by A, B, and C together in ‘x’ days.
Given, A and B together can do 60 % of whole work in ‘x’ days.
Therefore, Only C can do (100 − 60) % i.e. 40 % of whole work in ‘x’ days.
Again, B and C together can do 70 % of whole work in ‘x’ days.
Therefore, Only A can do (100 − 70) % i.e. 30 % of whole work in ‘x’ days.
Hence, Only B can do [100 − (40 + 30)] % i.e. 30 % of whole work in ‘x’ days.
Therefore, we can conclude from the above data that C is the most efficient. (Ans.)
Q.3) Three solid spheres of radius 3 cm, 4 cm and 5 cm are melted and recasted into a solid sphere. What will be the percentage decrease in the surface area ?
a) 12 %
b) 14 %
c) 16 %
d) 28 %
Answer
Correct Answer: (d) 28 %
Solution
After recasting into solid sphere, the radius become,
= (33 + 43 + 53)1⁄3
= (216)1⁄3
= 6 cm.
Now,
Total surface area of three spheres of radius 3 cm, 4 cm and 5 cm,
= 4π×32 + 4π×42 + 4π×52 sq.cm.
= 4π×(32 + 42 + 52) sq.cm.
= 200π sq.cm.
Surface area of recasted solid sphere,
= 4π×62 sq.cm.
= 200π sq.cm.
Percentage decrease in the surface area of recasted sphere,
=( 200π − 144π )⁄200π× 100 %
=56π⁄200π× 100 %
= 28 % (Ans.)
Q.4) The marked price of a sofa set is Rs 4800 which is sold at Rs 3672 at two successive discounts. If the first discount is 10%, then what will be the second discount (in %) ?
a) 13 %
b) 14 %
c) 15 %
d) 17 %
Answer
Correct Answer: (c) 15 %
Solution
Given,
Marked Price (M.P.) of sofa set = Rs. 4800
Selling Price (S.P.) of sofa set = Rs. 3672
Therefore, Total discount = Rs. (4800 − 3672) = Rs. 1128
Total discount (in %) = ( 1128⁄4800 )×100 % ⇒ 23.5 %
Let, the second discount be ‘x’ %.
Now, total discount (in %) after two successive discount,
= [10 + x − ( 10x⁄100 )] %
Note :
(1) If x and y are two successive discount then total discount percentage = [ x + y − (x × y)⁄100 ]%
(2) If x and y are two successive gain then total gain percentage = [ x + y + (x × y)⁄100 ]%
According to the problem (ATP),
[10 + x − ( 10x⁄100 )] % = 23.5 %
⇒ 10 + x − ( 10x⁄100 ) = 23.5
⇒ 10 × 100 + 100x − 10x = 23.5 × 100 [multiplying by 100 to the both sides]
⇒ x = 15
∴ The required second discount = 15 % (Ans.)
Q.5) A, B and C invested amounts in the ratio 3 : 4 : 5 respectively. If the schemes offered compound interest at the rate of 20% per annum, 15% per annum and 10% per annum respectively, then what will be the ratio of their amounts after 1 year ?
a) 3 : 15 : 25
b) 6 : 6 : 5
c) 36 : 46 : 55
d) 12 : 23 : 11
Answer
Correct Answer: (c) 36 : 46 : 55
Solution
Shortcut Approach :
The ratio of amount of A, B, and C (at the end of one year),
⇒ 3×(100 + 20) : 4×(100 + 15) : 5×(100 + 10)
⇒ 3×120 : 4×115 : 5×110
⇒ 36 : 46 : 55 (Ans.)
Q.6) The average age of 120 members of a society is 60.7 years. By addition of 30 new members, the average age becomes 56.3 years. What is the average age (in years) of newly joined members ?
a) 36.5
b) 37.2
c) 38.3
d) 38.7
Answer
Correct Answer: (d) 38.7
Solution
The total age of newly joined 30 mebers,
= [56.3 × (120 + 30) − 60.7 × 120] years
= (8445 − 7284) years
= 1161 years
⇒ The required average age of newly joined 30 members,
= 1161⁄30
= 38.7 years. (Ans.)
Q.7) By selling 175 pineapples, the gain is equal to the selling price of 50 pineapples. What is the gain percentage ?
a) 28 %
b) 30 %
c) 32 %
d) 40 %
Answer
Correct Answer: (d) 40 %
Solution
Let, the cost price (C.P.) of 1 pineapple = x and that of selling price (S.P.) = y
Therefore, S.P. of 50 pineapples = 50y
C.P. of 175 pineapples = 175x and that of S.P. = 175y
Thus, Profit by selling 175 pineapples,
⇒ 175y − 175x
= 175(y − x)
According to the question, we have
175(y − x) = 50y
⇒ y = 7x⁄5
Now, gain (in %),
= 175(y − x)⁄175x × 100 %
= (y − x)⁄x × 100 %
= (7x⁄5 − x)⁄x × 100 % [since, y = 7x⁄5]
= 40 %
Therefore, the required gain percentage = 40 % (Ans.)
Q.8) If A has got 20% more marks than B, then by what percent marks of B are less than the marks of A ?
a) 16.67 %
b) 20 %
c) 33.33 %
d) 14.28 %
Answer
Correct Answer: (a) 16.67 %
Solution
Let, B has got = 100 marks.
Therefore, A’s marks = (100 + 20) i.e. 120 marks.
Hence, B’s marks is less by (120 − 100) i.e. 20 marks than A’s marks.
Therefore, the required percentage = 20⁄120 × 100 % ⇒ 16.67 % (approx) (Ans.)
Q.9) A train leaves Delhi at 10 a.m. and reaches Jaipur at 4 p.m. on same day. Another train leaves Jaipur at 12 p.m. and reaches Delhi at 5 p.m. on same day. What is the time of day (approximately) when the two trains will meet ?
a) 1:42 p.m.
b) 1:27 p.m.
c) 2:04 p.m.
d) 1:49 p.m.
Answer
Correct Answer: (d) 1:49 p.m.
Solution
Total time taken to by 1st train to reach Jaipur from Delhi,
= (4 p.m. − 10 a.m.)
= 6 hours.
Total time taken to by 2nd train to reach Delhi from Jaipur,
= (5 p.m. − 12 p.m.)
= 5 hours.
Now, taking L.C.M. of 6 and 5 which is = 30
Let, total distance between Delhi and Jaipur = 30x kms
Therefore,
Speed of 1st train = 30x⁄6 ⇒ 5x km/hr [using, Speed = Distance⁄Total time]
Speed of 2nd train = 30x⁄5 ⇒ 6x km/hr
Now,
In 2 hours (10 p.m. to 12 p.m.), the distance covered by 1st train = 5x × 2 = 10x kms
Thus, the remaining path = (30x − 10x) kms ⇒ 20x kms
The relative speed of two trains = (5x + 6x) km/hr ⇒ 11x km/hr
Therefore, time taken to meet each other,
⇒ 20x⁄11x hours
= ( 20x⁄11x ) × 60 minutes
= 109 minutes (approx)
= 1 hr 49 minutes.
∴ The required time at which they will met,
= (12 p.m. + 1 hr 49 min)
= 1:49 p.m. (Ans.)
Q.10) The difference between the compound interest compounding half yearly for 1 year and the simple interest for 1 year on a certain sum of money lent out at 8% per annum is Rs 64. What is the sum (in Rs) ?
a) 40000
b) 42000
c) 44000
d) 44800
Answer
Correct Answer: (a) 40000
Solution
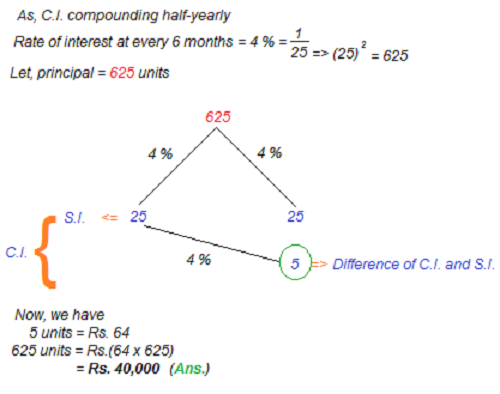
∵ Compound interest compounding half-yearly.
∴ Number of installments (in one year) = 2
Let, the principal = P
Compound Interest (C.I.) at the end of one year,
⇒ P[1 + { ( r⁄2 )⁄100 } ]2 − P
Note:
C.I. = P[1 + { ( r⁄y )⁄100 } ]t × y
Where, P = Principal; t = time (in year); r = rate of interest (per annum) and y = number of installment in one year
= P[1 + { ( 8⁄2 )⁄100 } ]2 − P
= 51P⁄625
Again,
Simple interest (S.I.) at the end of one year,
⇒ (P × t × r)⁄100
= (P × 1 × 8)⁄100
= 2P⁄25
According to the question, we have
51P⁄625 − 2P⁄25 = 64
⇒ P = Rs. 40,000 (Ans.)
Shortcut Approach :
Q.11) If (x − 2) and (x + 3) are the factors of the equation x2 + k1x + k2 = 0, then what are the values of k1 and k2 ?
a) k1 = 6, k2 = − 1
b) k1 = 1, k2 = − 6
c) k1 = 1, k2 = 6
d) k1 = − 6, k2 = 1
Answer
Correct Answer: (b) k1 = 1, k2 = − 6
Solution
Since, (x − 2) and (x + 3) are two factors of the given equation.
Therefore, the given equation x2 + k1x + k2 = 0 will be satisfied by x − 2 = 0 ⇒ x = 2 and x + 3 = 0 ⇒ x = − 3
Now, putting x = 2 into the given equatiion, we have
⇒ x2 + k1x + k2 = 0
⇒ 22 + 2k1 + k2 = 0
⇒ 2k1 + k2 = − 4 ————(1)
Putting x = − 3 into the given equation, we have
⇒ x2 + k1x + k2 = 0
⇒ (− 3)2 + (− 3)k1 + k2 = 0
⇒ 3k1 − k2 = 9 ————(2)
Now, by solving two equations, we have
k1 = 1 and k2 = − 6 (Ans.)
Q.12) If (x − y) = 7, then what is the value of (x − 15)3</sup/> − (y − 8)3 ?
a) 0
b) 343
c) 392
d) 2863
Answer
Correct Answer: (a) 0
Solution
Let, x − 15 = a ——– (1) and
y − 8 = b ——– (2)
Now, subtracting both the above equation, we have
(x − 15) − (y − 8) = a − b
⇒ x − y − 7 = a − b
⇒ 7 − 7 = a − b [∵ x − y = 7]
⇒ a − b = 0
⇒ (a − b)(a2 + ab + b2) = 0 × (a2 + ab + b2) [multiplying by (a2 + ab + b2) to the both sides]
⇒ a3 − b3 = 0
Now substituting the value of ‘a’ and ‘b’, we have
⇒ (x − 15)3 − (y − 8)3 = 0 (Ans.)
Shortcut Approach :
Given,
x – y = 7
Now, take y = 0
Therefore, x = 7
Now,
(x − 15)3 − (y − 8)3
= (7 − 15)3 − (0 − 8)3
= 0 (Ans.)
Q.13) If x − y − √18 = −1 and x + y − 3√2 = 1, then what is the value of 12xy(x2 − y2) ?
a) 0
b) 1
c) 512√2
d) 612√2
Answer
Correct Answer: (d) 612√2
Solution
x − y − √18 = −1
=> x − y − 3√2 = 1
=> x − y = 3√2 + 1 ———(1) and
x + y − 3√2 = 1
=> x + y = 3√2 + 1———- (2)
Now, clearly we can say,
x = 3√2 and y = 1 [applying identity property]
Now, putting the value of ‘x’ and ‘y’ into the required mathematical expression,
12xy(x2 − y2)
=> 12 × (3√2) × (1) × [(3√2)2 − (1)2]
= 612√2 (Ans.)
Q.14) If p⁄q = r⁄s = t⁄u = √5, then what is the value of ( 3p2 + 4r2 + 5t2 )⁄( 3q2 + 4s2 + 5u2 ) ?
a) ⅕
b) 5
c) 25
d) 60
Answer
Correct Answer: (b) 5
Solution
Shortcut Approach :
Let, u = s = q = 1
∴ p = r = t = √5
⇒ p2 = r2 = t2 = 5
∴ The required ratio => ( 3p2 + 4r2 + 5t2 )⁄( 3q2 + 4s2 + 5u2 )
⇒ ( 3 × 5 + 4 × 5 + 5 × 5 )⁄( 3 × 1 + 4 × 1 + 5 × 1 )
⇒ 5 (Ans.)
Q.15) In triangle ABC, a line is drawn from the vertex A to a point D on BC. If BC = 9 cm and DC = 3 cm, then what is the ratio of the areas of triangle ABD and triangle ADC respectively ?
a) 1 : 1
b) 2 : 1
c) 3 : 1
d) 4 : 1
Answer
Correct Answer: (b) 2 : 1
Solution
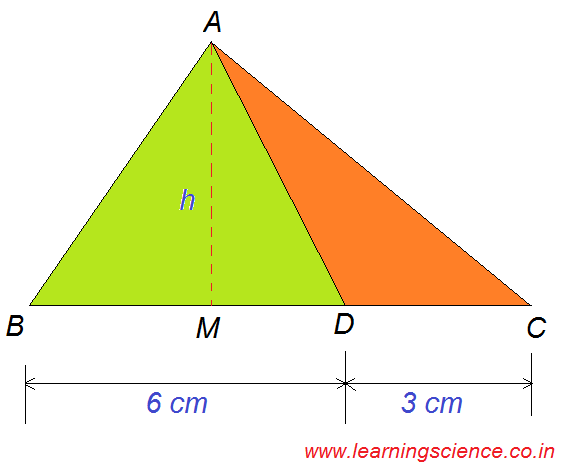
Construction : A line is drawn from point A such that AM⊥BD where AM = h (say)
Now, Area of ∆ABD,
= ½ × BD × AM sq.cm.
= ½ × 6 × h sq.cm.
= 6h⁄2 sq.cm.
Area of ∆ADC,
= ½ × CD × AM sq.cm.
= ½ × 3 × h sq.cm.
= 3h⁄2 sq.cm.
∴ The required ratio = 6h⁄2 : 3h⁄2
= 2 : 1 (Ans.)
Q.16) PQR is a right angled triangle in which ∠R = 90°. If RS ⊥ PQ, PR = 3 cm and RQ = 4 cm, then what is the value of RS (in cm) ?
a) 12⁄5
b) 36⁄5
c) 5
d) 2.5
Answer
Correct Answer: (a) 12⁄5
Solution
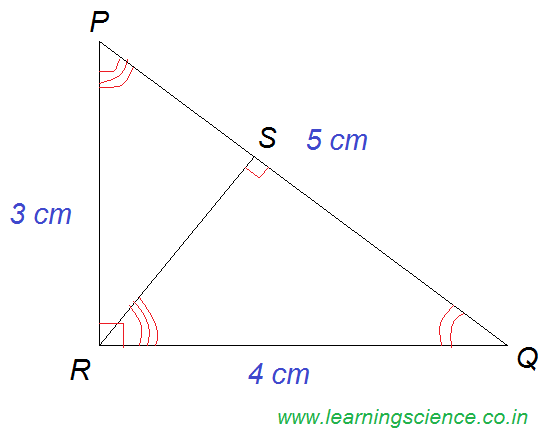
∵ ∆RSQ and ∆PRQ are similar.
∴ RQ⁄PQ = RS⁄PR
⇒ 4⁄5 = RS⁄3
∴ RS = 12⁄5 cm. (Ans.)
Special Note:
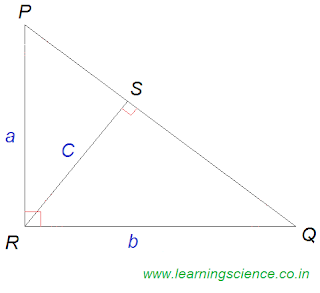
=> C = ( a × b )⁄√(a2 + b2)
Q.17) In triangle PQR, A is the point of intersection of all the altitudes and B is the point of intersection of all the angle bisectors of the triangle. If ∠PBR = 105°, then what is the value of ∠PAR (in degrees) ?
a) 60
b) 100
c) 105
d) 115
Answer
Correct Answer: (a) 60
Solution
Please keep patience, I am still working on it.
Q.18) If there are four lines in a plane, then what cannot be the number of points of intersection of these lines ?
a) 0
b) 5
c) 4
d) 7
Answer
Correct Answer: (d) 7
Solution
Please keep patience, I am still working on it.
Q.19) What is the simplified value of cosec 2A + cot 2A ?
a) sec A
b) sec A⁄2
c) cot A
d) cot 2A
Answer
Correct Answer: (c) cot A
Solution
Please keep patience, I am still working on it.
Q.20) If A = 30°, B = 60° and C = 135°, then what is the value of sin 3A + cos 3B + tan3C − 3sin A.cos B.tan C ?
a) 0
b) 1
c) 8
d) 9
Answer
Correct Answer: (a) 0
Solution
Please keep patience, I am still working on it.
Q.21) What is the least value of tan22θ + cot2θ + sin2θ + cos2θ + sec2θ + cosec2θ ?
a) 1
b) 3
c) 5
d) 7
Answer
Correct Answer: (d) 7
Solution
Please keep patience, I am still working on it.
Q.22) The Pie chart given below shows the break-up of number of hours of teaching various subjects at an institute by Mr. Raghav.
If Mr. Raghav taught a total of 500 hours, then what is the difference in number of hours of teaching algebra and modern Maths ?
a) 15
b) 20
c) 25
d) 40
Answer
Correct Answer: (c) 25
Solution
Please keep patience, I am still working on it.
Q.23) The Pie chart given below shows the break-up of number of hours of teaching various subjects at an institute by Mr. Raghav.
Mr. Raghav taught Geometry for 36 hours. If the time taken in teaching Ratio constitutes one-fourth of the time for Arithmetic, then for how much time (in hours) did he taught the topic of Ratio ?
a) 46
b) 51.75
c) 69
d) 103.5
Answer
Correct Answer: (c) 69
Solution
Please keep patience, I am still working on it.
Q.24) The Pie chart given below shows the break-up of number of hours of teaching various subjects at an institute by Mr. Raghav.
If Data Interpretation and Modern Maths were taught for a combined time of 96 hours, then for how much time (in hours) were Number system and Geometry taught ?
a) 136
b) 184
c) 216
d) 232
Answer
Correct Answer: (d) 232
Solution
Please keep patience, I am still working on it.
Q.25) The Pie chart given below shows the break-up of number of hours of teaching various subjects at an institute by Mr. Raghav.
A new topic named Problem Solving was also introduced and it was decided that 10% time of all topics except Arithmetic will be devoted to it. What will be the central angle (in degrees) made by Problem Solving in the new pie chart ?
a) 17.28
b) 36
c) 19.44
d) 18
Answer
Correct Answer: (c) 19.44
Solution
Please keep patience, I am still working on it.
If you still have any query then feel free to contact or comment below. I will definitely try to solve your issue. Thank you.
SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1, SSC CGL Held on 9th August 2017 Shift 1,