Koshe Dekhi 26.2 Class 10 |
Koshe Dekhi 26.2 Class 10
Q.1) মধুবাবুর দোকানের গত সপ্তাহের প্রতিদিনের বিক্রয়লব্ধ অর্থ (টাকায়) হলো, 107,210, 92, 52, 113, 75, 195; বিক্রয়লব্ধ অর্থের মধ্যমা নির্ণয় করি। সমাধানঃ প্রদত্ত মধুবাবুর দোকানের বিক্রয়লব্ধ অর্থকে (টাকায়) মানের ঊর্ধক্রমে সাজিয়ে পাই, 52, 75, 92, 107, 113, 195, 210 এখানে, পরিসংখ্যা (n) = 7 যা একটি অযুগ্ম সংখ্যা। ∴ বিক্রয়লব্ধ অর্থের মধ্যমা, = 4 তম পদ = 107 টাকা। উত্তরঃ নির্ণেয় মধুবাবুর দোকানের বিক্রয়লব্ধ অর্থের মধ্যমা 107 টাকা। তম পদ
তম পদ
Koshe Dekhi 26.2 Class 10
Q.2) কিছু পশুর বয়স (বছরে) হলো, 6, 10, 5, 4, 9, 11, 20, 18; বয়সের মধ্যমা নির্ণয় করি। সমাধানঃ প্রদত্ত পশুর বয়সকে (বছরে) মানের ঊর্ধক্রমে সাজিয়ে পাই, 4, 5, 6, 9, 10, 11, 18, 20 এখানে, পরিসংখ্যা (n) = 8 যা একটি যুগ্ম সংখ্যা। ∴ পশুর বয়সের মধ্যমা, = 9.5 বছর। উত্তরঃ নির্ণেয় পশুগুলির বয়সের মধ্যমা 9.5 বছর। Koshe Dekhi 26.2 Class 10 [
তম পদ +
তম পদ ]
[
তম পদ +
তম পদ ]
[ 4 তম পদ + 5 তম পদ ]
[ 9 + 10 ]
Q.3) 14 জন ছাত্রের প্রাপ্ত নম্বর হলো, 42, 51, 56, 45, 62, 59, 50, 52, 55, 64, 45, 54, 58, 60; প্রাপ্ত নম্বরের মধ্যমা নির্ণয় করি। সমাধানঃ প্রদত্ত 14 জন ছাত্রের প্রাপ্ত নম্বরগুলি মানের ঊর্ধক্রমে সাজিয়ে পাই, 42, 45, 45, 50, 51, 52, 54, 55, 56, 58, 59, 60, 62, 64 এখানে, পরিসংখ্যা (n) = 14 যা একটি যুগ্ম সংখ্যা। ∴ ছাত্রগুলির প্রাপ্ত নম্বরের মধ্যমা, = 54.5 উত্তরঃ নির্ণেয় 14 জন ছাত্রের প্রাপ্ত নম্বরের মধ্যমা 54.5 [
তম পদ +
তম পদ ]
[
তম পদ +
তম পদ ]
[ 7 তম পদ + 8 তম পদ ]
[ 54 + 55 ]
Koshe Dekhi 26.2 Class 10
Q.4) আজ পাড়ার ক্রিকেট খেলায় আমাদের স্কোর হলো, 7, 9, 10, 11, 11, 8, 7, 7, 10, 6, 9, 7, 9, 9, 6, 6, 8, 8, 9, 8, 7, 8 ক্রিকেট খেলায় আমাদের স্কোরের মধ্যমা নির্ণয় করি। সমাধানঃ প্রদত্ত ক্রিকেট স্কোরগুলিকে মানের ঊর্ধক্রমে সাজিয়ে পাই, 6, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 8, 8, 9, 9, 9, 9, 9, 10, 10, 11, 11 এখানে, পরিসংখ্যা (n) = 22 যা একটি যুগ্ম সংখ্যা। ∴ ছাত্রগুলির প্রাপ্ত স্কোরের মধ্যমা, = 8 উত্তরঃ নির্ণেয় ক্রিকেট খেলায় আমাদের স্কোরের মধ্যমা 8 [
তম পদ +
তম পদ ]
[
তম পদ +
তম পদ ]
[ 11 তম পদ + 12 তম পদ ]
[ 8 + 8 ]
Koshe Dekhi 26.2 Class 10
Q.5) নীচের 70 জন ছাত্রের ওজনের পরিসংখ্যা বিভাজন ছক থেকে ওজনের মধ্যমা নির্ণয় করি। সমাধানঃ এখানে, পরিসংখ্যা (n) = 70 যা একটি যুগ্ম সংখ্যা। ∴ ছাত্রগুলির ওজনের মধ্যমা = 47 উত্তরঃ নির্ণেয় 70 জন ছাত্রের ওজনের মধ্যমা 47 কিগ্ৰা। 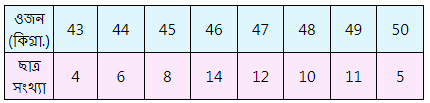

[
তম পদ +
তম পদ ]
[
তম পদ +
তম পদ ]
[ 35 তম পদ + 36 তম পদ ]
[ 47 + 47 ]
Koshe Dekhi 26.2 Class 10
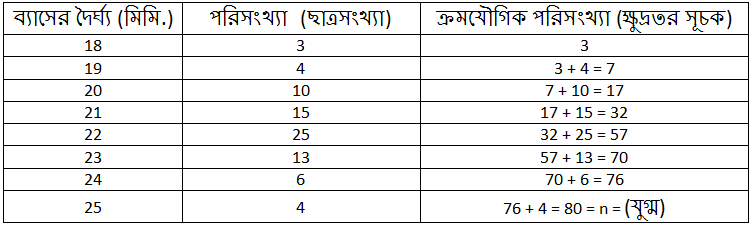
Q.6) নলের ব্যাসের দৈর্ঘ্যের (মিমি) পরিসংখ্যা বিভাজন ছক থেকে ব্যাসের দৈর্ঘ্যের মধ্যমা নির্ণয় করি। সমাধানঃ এখানে, পরিসংখ্যা (n) = 80 যা একটি যুগ্ম সংখ্যা। ∴ নলগুলির ব্যাসের দৈর্ঘ্যের মধ্যমা = 22 উত্তরঃ নির্ণেয় নলের ব্যাসের দৈর্ঘ্যের মধ্যমা 22 মিমি.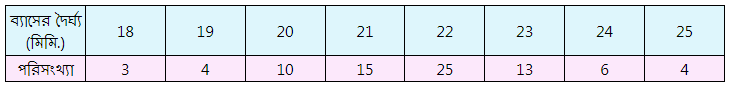
[
তম পদ +
তম পদ ]
[
তম পদ +
তম পদ ]
[ 40 তম পদ + 41 তম পদ ]
[ 22 + 22 ]
Koshe Dekhi 26.2 Class 10
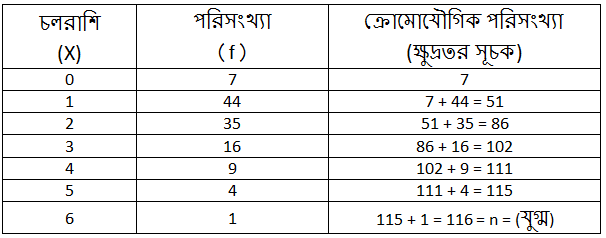
Q.7) মধ্যমা নির্ণয় করিঃ সমাধানঃ এখানে, পরিসংখ্যা (n) = 116 যা একটি যুগ্ম সংখ্যা। ∴ চলরাশিগুলির মধ্যমা = 2 উত্তরঃ নির্ণেয় চলরাশিগুলির মধ্যমা 2
x
0
1
2
3
4
5
6
f
7
44
35
16
9
4
1
[
তম পদ +
তম পদ ]
[
তম পদ +
তম পদ ]
[ 58 তম পদ + 59 তম পদ ]
[ 2 + 2 ]
Koshe Dekhi 26.2 Class 10
Q.8) আমাদের 40 জন শিক্ষার্থীর প্রতি সপ্তাহে টিফিন খরচের (টাকায়) পরিসংখ্যা হলো, টিফিন খরচের মধ্যমা নির্ণয় করি। সমাধানঃ এখানে, মোট পরিসংখ্যা (n) = 40 যা একটি যুগ্ম সংখ্যা। সুতরাং, মধ্যমা শ্রেণি হলো “50 – 55” l = 50 = মধ্যমা শ্রেণির নিম্ন সীমানা। n = 40 = পর্যবেক্ষণ সংখ্যা। C.F. = 14 = মধ্যমা শ্রেণির ঠিক আগের শ্রেণির ক্রোমোযৌগিক পরিসংখ্যা। f = 9 = মধ্যমা শ্রেণির পরিসংখ্যা। h = (55 − 50) = 5 = মধ্যমা শ্রেণির শ্রেণি দৈর্ঘ্য মধ্যমা উত্তরঃ নির্ণেয় 40 জন শিক্ষার্থীর প্রতি সপ্তাহে টিফিন খরচের (টাকায়) মধ্যমা 53.33 টাকা।
টিফিন খরচ (টাকায়)
35 – 40
40 – 45
45 – 50
50 – 55
55 – 60
60 – 65
65 – 70
শিক্ষার্থী
3
5
6
9
7
8
2
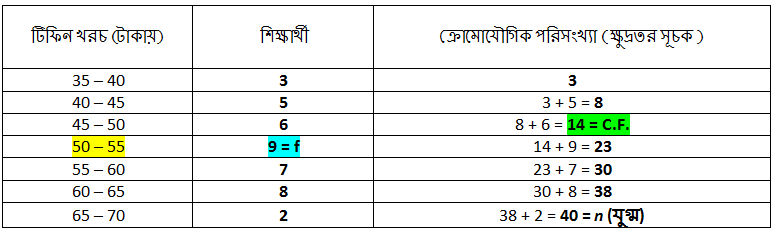
= 20 এর ঠিক বেশি ক্রোমোযৌগিক পরিসংখ্যা “50 – 55” এর মধ্যে আছে।
(প্রায়)
(প্রায়)
Koshe Dekhi 26.2 Class 10
Q.9) নীচের তথ্য থেকে ছাত্রদের উচ্চতার মধ্যমা নির্ণয় করি : সমাধানঃ এখানে, মোট পরিসংখ্যা (n) = 100 যা একটি যুগ্ম সংখ্যা। সুতরাং, মধ্যমা শ্রেণি হলো “150 – 155” l = 150 = মধ্যমা শ্রেণির নিম্ন সীমানা। n = 100 = পর্যবেক্ষণ সংখ্যা। C.F. = 35 = মধ্যমা শ্রেণির ঠিক আগের শ্রেণির ক্রোমোযৌগিক পরিসংখ্যা। f = 22 = মধ্যমা শ্রেণির পরিসংখ্যা। h = (155 − 150) = 5 = মধ্যমা শ্রেণির শ্রেণি দৈর্ঘ্য মধ্যমা = 150 + 3.409 (প্রায়) = 150 + 3.41 (প্রায়) = 153.41 (প্রায়) উত্তরঃ নির্ণেয় ছাত্রগুলির উচ্চতার মধ্যমা 153.41 সেমি (প্রায়)।
উচ্চতা (সেমি.)
135 – 140
140 – 145
145 – 150
150 – 155
155 – 160
160 – 165
165 – 170
ছাত্রদের সংখ্যা
6
10
19
22
20
16
7
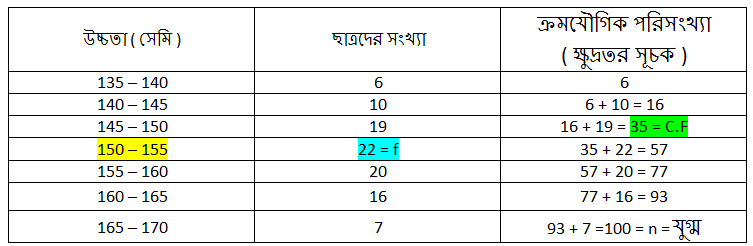
এর ঠিক বেশি ক্রোমোযৌগিক পরিসংখ্যা “150 – 155” এর মধ্যে আছে।
Koshe Dekhi 26.2 Class 10
Q.10) নীচের পরিসংখ্যা বিভাজন থেকে তথ্যটির মধ্যমা নির্ণয় করি : সমাধানঃ এখানে, মোট পরিসংখ্যা (n) = 59 যা একটি অযুগ্ম সংখ্যা। সুতরাং, মধ্যমা শ্রেণি হলো “30 – 40” l = 30 = মধ্যমা শ্রেণির নিম্ন সীমানা। n = 59 = পর্যবেক্ষণ সংখ্যা। C.F. = 21 = মধ্যমা শ্রেণির ঠিক আগের শ্রেণির ক্রোমোযৌগিক পরিসংখ্যা। f = 15 = মধ্যমা শ্রেণির পরিসংখ্যা। h = (40 − 30) = 10 = মধ্যমা শ্রেণির শ্রেণি দৈর্ঘ্য মধ্যমা = 30 + 5.6666 (প্রায়) = 30 + 5.67 (প্রায়) = 35.67 (প্রায়) উত্তরঃ নির্ণেয় মধ্যমা 35.67 (প্রায়)
শ্রেণী-সীমানা
0 – 10
10 – 20
20 – 30
30 – 40
40 – 50
50 – 60
60 – 70
পরিসংখ্যা
4
7
10
15
10
8
5
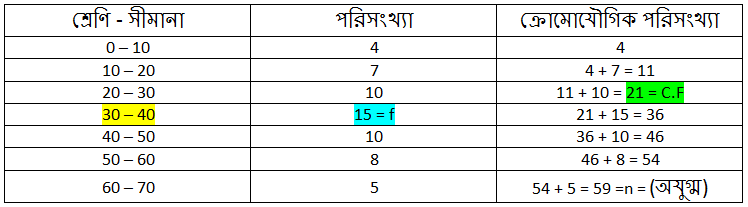
এর ঠিক বেশি ক্রোমোযৌগিক পরিসংখ্যা “30 – 40” এর মধ্যে আছে।
Koshe Dekhi 26.2 Class 10
Q.11) নীচের তথ্যের মধ্যমা নির্ণয় করি : সমাধানঃ এখানে, মোট পরিসংখ্যা (n) = 50 যা একটি যুগ্ম সংখ্যা। সুতরাং, মধ্যমা শ্রেণি হলো “15 – 20” l = 15 = মধ্যমা শ্রেণির নিম্ন সীমানা। n = 50 = পর্যবেক্ষণ সংখ্যা। C.F. = 11 = মধ্যমা শ্রেণির ঠিক আগের শ্রেণির ক্রোমোযৌগিক পরিসংখ্যা। f = 15 = মধ্যমা শ্রেণির পরিসংখ্যা। h = (20 − 15) = 5 = মধ্যমা শ্রেণির শ্রেণি দৈর্ঘ্য মধ্যমা = 15 + 4.666 (প্রায়) = 15 + 4.67 (প্রায়) = 19.67 (প্রায়) উত্তরঃ নির্ণেয় মধ্যমা 19.67 (প্রায়)
শ্রেণী-সীমানা
5 – 10
10 – 15
15 – 20
20 – 25
25 – 30
30 – 35
35 – 40
40 – 45
পরিসংখ্যা
5
6
15
10
5
4
3
2
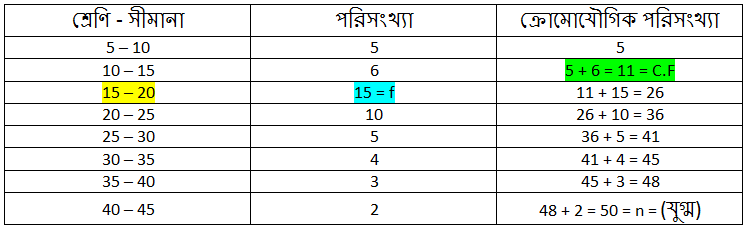
এর ঠিক বেশি ক্রোমোযৌগিক পরিসংখ্যা “15 – 20” এর মধ্যে আছে।
Koshe Dekhi 26.2 Class 10
Q.12) নীচের তথ্যের মধ্যমা নির্ণয় করি : সমাধানঃ এখানে, মোট পরিসংখ্যা (n) = 30 যা একটি যুগ্ম সংখ্যা। \( \frac{71}{2}=35.5 \) এর ঠিক বেশি ক্রোমোযৌগিক পরিসংখ্যা “15.5 – 20.5” এর মধ্যে আছে। সুতরাং, মধ্যমা শ্রেণি হলো “15.5 – 20.5” l = 15.5 = মধ্যমা শ্রেণির নিম্ন সীমানা। n = 71 = পর্যবেক্ষণ সংখ্যা। C.F. = 29 = মধ্যমা শ্রেণির ঠিক আগের শ্রেণির ক্রোমোযৌগিক পরিসংখ্যা। f = 20 = মধ্যমা শ্রেণির পরিসংখ্যা। h = (20.5 − 15.5) = 5 = মধ্যমা শ্রেণির শ্রেণি দৈর্ঘ্য মধ্যমা = 15.5 + 1.625 (প্রায়) = 17.125 (প্রায়) = 17.13 (প্রায়) উত্তরঃ নির্ণেয় মধ্যমা 17.13 (প্রায়)
শ্রেণী-সীমা
1 – 5
6 – 10
11 – 15
16 – 20
21 – 25
26 – 30
31 – 35
পরিসংখ্যা
4
10
15
20
15
4
3
শ্রেণি-সীমা
শ্রেনি-সীমানা
পরিসংখ্যা
ক্রোমোযৌগিক পরিসংখ্যা
1 – 5
0.5 – 5.5
4
4
6 – 10
5.5 – 10.5
10
4 + 10 = 14
11 – 15
10.5 – 15.5
15
14 + 15 = 29 = C.F
16 – 20
15.5 – 20.5
20 = f
29 + 20 = 49
21 – 25
20.5 – 25.5
15
49 + 15 = 64
26 – 30
25.5 – 30.5
4
64 + 4 = 68
31 – 35
30.5 – 35.5
3
68 + 3 = 71 = n
Koshe Dekhi 26.2 Class 10
Q.13) নীচের তথ্যের মধ্যমা নির্ণয় করি : সমাধানঃ এখানে, মোট পরিসংখ্যা (n) = 68 যা একটি যুগ্ম সংখ্যা। সুতরাং, মধ্যমা শ্রেণি হলো “80.5 – 90.5” l = 80.5 = মধ্যমা শ্রেণির নিম্ন সীমানা। n = 68 = পর্যবেক্ষণ সংখ্যা। C.F. = 29 = মধ্যমা শ্রেণির ঠিক আগের শ্রেণির ক্রোমোযৌগিক পরিসংখ্যা। f = 20 = মধ্যমা শ্রেণির পরিসংখ্যা। h = (90.5 − 80.5) = 10.0 = মধ্যমা শ্রেণির শ্রেণি দৈর্ঘ্য মধ্যমা = 80.5 + 2.5 = 83 উত্তরঃ নির্ণেয় মধ্যমা 83
শ্রেণী-সীমা
51 – 60
61 – 70
71 – 80
81 – 90
91 – 100
101 – 110
পরিসংখ্যা
4
10
15
20
15
4

এর ঠিক বেশি ক্রোমোযৌগিক পরিসংখ্যা “80.5 – 90.5” এর মধ্যে আছে।
Koshe Dekhi 26.2 Class 10
Q.14) নীচের তথ্যের মধ্যমা নির্ণয় করি : সমাধানঃ এখানে, মোট পরিসংখ্যা (n) = 120 যা একটি যুগ্ম সংখ্যা। সুতরাং, মধ্যমা শ্রেণি হলো “40 – 50” l = 40 = মধ্যমা শ্রেণির নিম্ন সীমানা। n = 120 = পর্যবেক্ষণ সংখ্যা। C.F. = 60 = মধ্যমা শ্রেণির ঠিক আগের শ্রেণির ক্রোমোযৌগিক পরিসংখ্যা। f = 12 = মধ্যমা শ্রেণির পরিসংখ্যা। h = 50 – 40 = 10 = মধ্যমা শ্রেণির শ্রেণি দৈর্ঘ্য মধ্যমা = 40 + 0 = 40 উত্তরঃ নির্ণেয় মধ্যমা 40
নম্বর
ছাত্রীদের সংখ্যা
10 -এর কম
12
20 -এর কম
22
30 -এর কম
40
40 -এর কম
60
50 -এর কম
72
60 -এর কম
87
70 -এর কম
102
80 -এর কম
111
90 -এর কম
120

এর ঠিক বেশি ক্রোমোযৌগিক পরিসংখ্যা “40 – 50” এর মধ্যে আছে।
Koshe Dekhi 26.2 Class 10
Q.15) নীচের তথ্যের মধ্যমা 32 হলে, x ও y-এর মান নির্ণয় করি যখন পরিসংখ্যার সমষ্টি 100; সমাধানঃ যেহেতু প্রদত্ত তথ্যের মধ্যমা 32 , সুতরাং, মধ্যমা শ্রেণি হবে 30 – 40 এখানে, মোট পরিসংখ্যা (n) = 100 যা একটি যুগ্ম সংখ্যা। সুতরাং, মধ্যমা শ্রেণি হলো “30 – 40” l = 30 = মধ্যমা শ্রেণির নিম্ন সীমানা। n = 100 = পর্যবেক্ষণ সংখ্যা। C.F. = 35 + x = মধ্যমা শ্রেণির ঠিক আগের শ্রেণির ক্রোমোযৌগিক পরিসংখ্যা। f = 30 = মধ্যমা শ্রেণির পরিসংখ্যা। h = 40 – 30 = 10 = মধ্যমা শ্রেণির শ্রেণি দৈর্ঘ্য মধ্যমা বা, বা, বা, বা, বা, 6 = 15 – x বা, x = 15 – 6 ∴ x = 9 আবার, 75 + x + y = 100 বা, 75 + 9 + y = 100 বা, y = 100 – 84 ∴ y = 16 উত্তরঃ নির্ণেয় x ও y-এর মান যথাক্রমে 9 ও 16
শ্রেণী-সীমানা
পরিসংখ্যা
0 – 10
10
10 – 20
x
20 – 30
25
30 – 40
30
40 – 50
y
50 – 60
10

এর ঠিক বেশি ক্রোমোযৌগিক পরিসংখ্যা “40 – 50” এর মধ্যে আছে।
Koshe Dekhi 26.2 Class 10
Koshe Dekhi 26.2 Class 10
মধ্যমা

Naushbshs
T hanks sir nice 👍🙂👍🙂👍🙂👍🙂👍🙂👍🙂👍🙂👍🙂👍🙂👍🙂👍🙂👍🙂👍🙂🙂🙂👍🙂🙂🙂👍🙂🙂🙂🙂🙂👍👍🙂👍👍🙂👍👍
most welcome
Amazing and wonderful