Koshe Dekhi 10 class 10
Koshe Dekhi 10 class 10
Q1. পাশের ছবির PQRS বৃত্তস্থ চতুর্ভুজের কর্ণদ্বয় পরস্পরকে X বিন্দুতে এমনভাবে ছেদ করেছে যে ∠PRS = 65° এবং ∠RQS = 45°; ∠SQP ও ∠RSP -এর মান হিসাব করে লিখি।
উত্তর : ∠SQP = 45° এবং ∠RSP = 90° সমাধানঃ |
| Q2. ABCD বৃত্তস্থ চতুর্ভুজের AB বাহুকে X বিন্দু পর্যন্ত বর্ধিত করলাম এবং মেপে দেখছি ∠XBC = 82° এবং ∠ADB = 47°; ∠BAC -এর মান হিসাব করে লিখি।
উত্তর : ∠BAC = 35° সমাধানঃ |
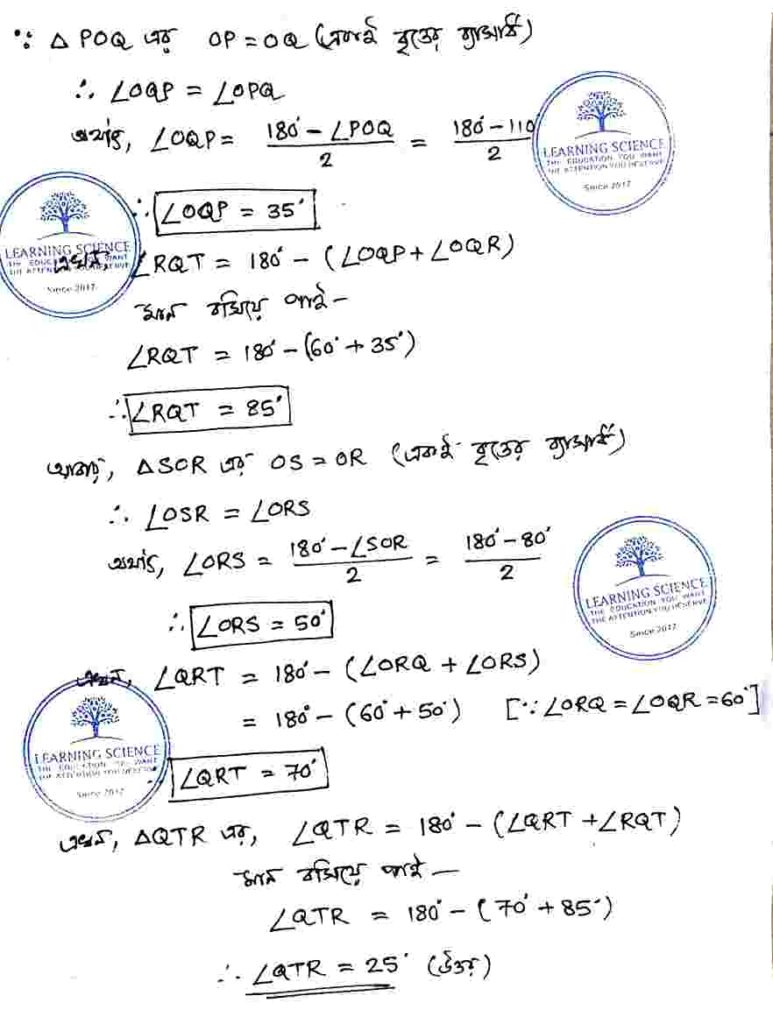
| Q3. PQRS বৃত্তস্থ চতুর্ভুজের PQ, SR বাহু দুটি বর্ধিত করায় T বিন্দুতে মিলিত হলো। বৃত্তের কেন্দ্র O; ∠POQ = 110°, ∠QOR = 60°, ∠ROS = 80° হলে ∠RQS ও ∠QTR -এর মান হিসাব করে লিখি।
উত্তর : ∠RQS = 40° ও ∠QTR = 25° সমাধানঃ |
| Q4. দুটি বৃত্ত পরস্পরকে P ও Q বিন্দুতে ছেদ করেছে। P ও Q বিন্দুগামী দুটি সরলরেখা একটি বৃত্তকে যথাক্রমে A ও C এবং অপর বৃত্তকে যথাক্রমে B ও D বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, AC || BD.
সমাধানঃ |
Support Me
If you like my work then you can Support me by contributing a small amount which will help me a lot to grow my channel. It’s a request to all of you. You can donate me through phone pay / Paytm/ Gpay on this number 7980608289 or by the link below :
| Q5. ABCD একটি বৃত্তস্থ চতুর্ভুজ অঙ্কন করেছি এবং এর BC বাহুকে E বিন্দু পর্যন্ত বর্ধিত করলাম। প্রমাণ করি যে, ∠BAD ও ∠DCE -এর সমদ্বিখণ্ডকদ্বয় বৃত্তের উপর মিলিত হবে।
সমাধানঃ |
| Q6. মোহিত একটি বৃত্তের বহিঃস্থ কোনো বিন্দু দিয়ে দুটি সরলরেখা অঙ্কন করেছে যারা বৃত্তটিকে যথাক্রমে A, B বিন্দু ও C, D বিন্দুতে ছেদ করেছে। যুক্তি দিয়ে প্রমাণ করি যে, ΔXAC ও ΔXBD -এর দুটি করে কোণ সমান।
সমাধানঃ |
| Q7. দুটি বৃত্ত অঙ্কন করেছি যারা পরস্পরকে G ও H বিন্দুতে ছেদ করেছে। এবার G বিন্দুগামী একটি সরলরেখা অঙ্কন করলাম যেটি বৃত্ত দুটিকে P ও Q বিন্দুতে এবং H বিন্দুগামী PQ -এর সমান্তরাল অপর একটি সরলরেখা অঙ্কন করলাম যা বৃত্তদুটিকে R ও S বিন্দুতে ছেদ করল। প্রমাণ করি যে, PQ = RS.
সমাধানঃ |
| Q8. ABC একটি ত্রিভুজ অঙ্কন করেছি যার AB = AC এবং বর্ধিত BC -এর উপর E যে-কোনো একটি বিন্দু। ΔABC -এর পরিবৃত্ত AE -কে D বিন্দুতে ছেদ করলে প্রমাণ করি যে, ∠ACD = ∠AEC.
সমাধানঃ |
| Q9. ABCD একটি বৃত্তস্থ চতুর্ভুজ। DE জ্যা ∠BDC -এর বহির্দ্বিখণ্ডক। প্রমাণ করি যে, AE (বা বর্ধিত AE) ∠BAC -এর বহির্দ্বিখণ্ডক।
সমাধানঃ
বৃত্তস্থ চতুর্ভুজ ABCD -এর ∠BDC -এর বহির্দ্বিখণ্ডক DE জ্যা। প্রমাণ করতে হবে যে, AE হলো ∠BAC -এর বহির্দ্বিখণ্ডক। অঙ্কনঃ CD কে Y পর্যন্ত এবং BA কে X পর্যন্ত বর্ধিত করা হল। প্রমাণঃ বৃত্তস্থ চতুর্ভুজ AEDB থেকে পাই, ∠EAX = ∠EDB — (i) [যেহেতু, বৃত্তস্থ চতুর্ভুজের বহিঃস্থ কোন বিপরীত অন্তঃস্থ কোনের সমান]
আবার যেহেতু, ED হলো ∠BDC -এর বহির্দ্বিখণ্ডক। ∴ ∠EDB = ∠EDY —- (ii) এখন (i) ও (ii) নং সমীকরণ তুলনা করে পাই, ∠EAX = ∠EDY —-(iii)
আবার, বৃত্তস্থ চতুর্ভুজ ACDE থেকে পাই, ∠EDY = ∠EAC —- (iv) [যেহেতু, বৃত্তস্থ চতুর্ভুজের বহিঃস্থ কোন বিপরীত অন্তঃস্থ কোনের সমান] (iii) ও (iv) নং সমীকরণ তুলনা করে পাই, ∠EAX = ∠EAC অর্থাৎ, EA, ∠BAC -এর বহির্দ্বিখণ্ডক।(প্রমানিত) |
| Q10. ABC ত্রিভুজের AC ও AB বাহুর উপর BE ও CF যথাক্রমে লম্ব। প্রমাণ করি যে, B, C, E, F বিন্দু চারটি সমবৃত্তস্থ। এর থেকে প্রমাণ করি যে, ΔAEF ও ΔABC -এর দুটি করে কোণ সমান।
সমাধানঃ
ABC ত্রিভুজের AC ও AB বাহুর উপর BE ও CF লম্ব। প্রমাণ করতে হবে যে, B, C, E, F বিন্দু সমবৃত্তস্থ। অতঃপর প্রমাণ করতে হবে যে, ΔAEF ও ΔABC -এর দুটি করে কোণ সমান। অঙ্কনঃ E, F যুক্ত করা হল। প্রমাণঃ যেহেতু, BE ⊥ AC, CF ⊥ AB [দেওয়া আছে] ∴ ∠BFC = 90°, ∠BEC = 90° এখন, ∠BFE + ∠BCE = ∠BFC + ∠CFE + ∠BCF + ∠ECF বা, ∠BFE + ∠BCE = 90° + ∠CFE + (90° – ∠CBF) + ∠ECF [∵ ∠BCF = 90° – ∠CBF] বা, ∠BFE + ∠BCE = 180° + ∠CFE – (∠FBE + ∠CBE) + ∠ECF [∵ ∠CBF = ∠FBE + ∠CBE] বা, ∠BFE + ∠BCE = 180° + ∠CFE – ∠FBE – ∠CBE + ∠ECF বা, ∠BFE + ∠BCE = 180° [∵ ∠CFE = ∠CBE, ∠FBE = ∠ECF] ∴ BCEF বৃত্তস্থ চতুর্ভুজ। ∴ B, C, E, F বিন্দু চারটি সমবৃত্তস্থ।
আবার, ∵ BCEF বৃত্তস্থ চতুর্ভুজের বহিঃস্থ কোণ ∠FEA = অন্তস্থ বিপরীত ∠CBF এবং বহিঃস্থ কোণ ∠AFE = অন্তস্থ বিপরীত ∠BCE ∴ △AEF ও △ABC -এর ∠FEA = ∠CBA এবং ∠AFE = ∠BCA ∴ △AEF ও △ABC -এর দুটি করে কোণ সমান। (প্রমানিত) |
Support Me
If you like my work then you can Support me by contributing a small amount which will help me a lot to grow my channel. It’s a request to all of you. You can donate me through phone pay / Paytm/ Gpay on this number 7980608289 or by the link below :
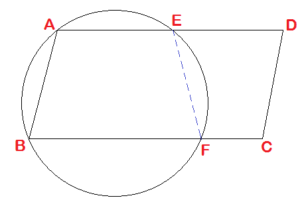
| Q11. ABCD একটি সামান্তরিক। A ও B বিন্দুগামী একটি বৃত্ত AD ও BC -কে যথাক্রমে E ও F বিন্দুতে ছেদ করে। প্রমাণ করি যে, E, F, C, D বিন্দু চারটি সমবৃত্তস্থ।
সমাধানঃ
ABCD সামান্তরিকের A ও B বিন্দুগামী একটি বৃত্ত AD ও BC কে যথাক্রমে E ও F বিন্দুতে ছেদ করেছে। প্রমাণ করতে হবে যে, E, F, C, D সমবৃত্তস্থ। অঙ্কনঃ E, F যুক্ত করা হল। প্রমাণঃ যেহেতু ABFE বৃত্তস্থ চতুর্ভুজ। ∴ ∠BAE + ∠BFE = 180° —— (i) [বৃত্তস্থ চতুর্ভুজের বিপরীত কোণ দুটির যোগফল 180°]
আবার, BC বাহুর ওপর F বিন্দুতে EF দন্ডায়মান ∴ ∠BFE + ∠EFC = 180° —— (ii)
এখন, (i) ও (ii) নং সমীকরণ থেকে পাই – ∠BAE + ∠BFE = ∠BFE + ∠EFC অর্থাৎ, ∠BAE = ∠EFC —— (iii)
আবার, যেহেতু ABCD সামন্তরিক ∴ ∠BAD + ∠ADC = 180° বা, ∠BAE + ∠EDC = 180° [∵ ∠BAD = ∠BAE (একই কোণ); ∠ADC = ∠EDC (একই কোণ)] বা, ∠EFC + ∠EDC = 180° [(iii) নং সমীকরণ অনুসারে]
এখন, আমরা যা পেলাম, DEFC চতুর্ভুজের ∠EFC + ∠EDC = 180° ∴ EFCD একটি বৃত্তস্থ চতুর্ভুজ। ∴ E, F, C, D বিন্দু চারটি সমবৃত্তস্থ।(প্রমানিত) |
| Q12. ABCD একটি বৃত্তস্থ চতুর্ভুজ। AB ও DC বাহুদ্বয়কে বর্ধিত করলে P বিন্দুতে এবং AD ও BC বাহুদ্বয়কে বর্ধিত করলে R বিন্দুতে মিলিত হয়। ΔBCP এবং ΔCDR -এর পরিবৃত্তদ্বয় T বিন্দুতে ছেদ করে। প্রমাণ করি যে, P, T, R সমরেখ।
সমাধানঃ
ABCD একটি বৃত্তস্থ চতুর্ভুজ যার AB ও DC বাহু দুটিকে বর্ধিত করলে তারা P বিন্দুতে এবং AD ও BC বাহু দুটিকে বর্ধিত করলে তারা R বিন্দুতে ছেদ করে। ΔBCP ও ΔCDR -এর পরিবৃত্তদ্বয় T বিন্দুতে ছেদ করে। প্রমাণ করতে হবে যে, P, T, R বিন্দু তিনটি সমরেখ। অঙ্কনঃ P, T; C, T ও R, T যুক্ত করা হল। প্রমাণঃ যেহেতু AR বাহুর ওপর D বিন্দুতে DC দন্ডায়মান ∴ ∠RDC + ∠ADC = 180° —- (i) আবার, ∵ DCTR বৃত্তস্থ চতুর্ভুজ। ∴ ∠RTC + ∠RDC = 180° —- (ii) [বৃত্তস্থ চতুর্ভুজের বিপরীত কোণ দুটির যোগফল 180°] এখন, (i) ও (ii) নং সমীকরণ থেকে পাই – ∴ ∠RTC + ∠RDC = ∠RDC + ∠ADC ∴ ∠RTC = ∠ADC —– (iii)
যেহেতু AP বাহুর ওপর B বিন্দুতে BC দন্ডায়মান ∴ ∠PBC + ∠ABC = 180° —- (iv) আবার, ∵ BCTP বৃত্তস্থ চতুর্ভুজ ∴ ∠PBC + ∠PTC = 180° —– (v) [বৃত্তস্থ চতুর্ভুজের বিপরীত কোণ দুটির যোগফল 180°] এখন, (iv) ও (v) নং সমীকরণ থেকে পাই – ∠PBC + ∠ABC = ∠PBC + ∠PTC ∴ ∠PTC = ∠ABC ——- (vi)
এখন, (iii) ও (vi) নং সমীকরণ যোগ করে পাই – ∠RTC + ∠PTC = ∠ADC + ∠ABC ∴ ∠RTC + ∠PTC = 180° [∵ ABCD বৃত্তস্থ চতুর্ভুজের ∠ADC ও ∠ABC হলো দুটি বিপরীত কোণ] এখন, আমরা যা পেলাম ∠PTC ও ∠RTC কোণ দুটির যোগফল 180° এবং একটি সাধারণ বাহু হলো CT. ∴ PT ও TR একই সরলরেখায় অবস্থিত। P, T, R সমরেখ।(প্রমানিত) |
| Q13. ABC ত্রিভুজের লম্ববিন্দু O; প্রমাণ করি যে O বিন্দুটি পাদত্রিভুজের অন্তঃকেন্দ্র।
সমাধানঃ
ধরি, ΔABC -এর A, B ও C বিন্দু তিনটি দিয়ে তাদের বিপরীত বাহুর ওপর অঙ্কিত লম্ব তিনটি হলো যথাক্রমে AD, BE ও CF যারা পরস্পরকে O বিন্দুতে ছেদ করেছে। D, E; E, F; F, D যোগ করা হল। প্রমাণ করতে হবে যে, O বিন্দুটি পাদত্রিভুজ ΔDEF -এর অন্তঃকেন্দ্র। প্রমাণঃ যেহেতু আমরা জানি, কোনো সূক্ষকোণী ত্রিভুজের শীর্ষবিন্দুগুলি থেকে তার বিপরীত বাহুর ওপর লম্ব অঙ্কন করলে তা পাদত্রিভুজের কোনগুলিকে সমদ্বিখন্ডিত করে। সুতরাং, ∠FDE -এর অন্তঃসমদ্বিখণ্ডক হলো AD, ∠DFE -এর অন্তঃসমদ্বিখণ্ডক হলো CF এবং ∠DEF -এর অন্তঃসমদ্বিখণ্ডক হলো BE. আবার, আমরা জানি যে, কোনো ত্রিভুজের কোনগুলির অন্তঃসমদ্বিখণ্ডকগুলি সমবিন্দু হয় এবং সেই নিদৃষ্ট বিন্দুটি হলো অন্তঃকেন্দ্র। ∴ পাদত্রিভুজ ΔDEF -এর অন্তঃকেন্দ্র হলো O. (প্রমানিত) |
| Q14. ABCD এমন একটি বৃত্তস্থ চতুর্ভুজ এঁকেছি যে AC, ∠BAD -কে সমদ্বিখণ্ডিত করেছে। এবার AD -কে E বিন্দু পর্যন্ত এমনভাবে বর্ধিত করলাম যেন DE = AB হয়। প্রমাণ করি যে, CE = CA.
সমাধানঃ
ABCD বৃত্তস্থ চতুর্ভুজের AC, ∠BAD -এর অন্তঃসমদ্বিখণ্ডক। AD কে E বিন্দু পর্যন্ত এমনভাবে বর্ধিত করা হলো যাতে DE = AB হয়। প্রমাণ করতে হবে যে, CE = CA অঙ্কনঃ B, D যুক্ত করা হল। প্রমাণঃ যেহেতু BC উপচাপ দ্বারা গঠিত দুটি বৃত্তস্থ কোণ হলো ∠BAC ও ∠BDC. ∴ ∠BAC = ∠BDC —- (i) [একই বৃত্যাংশস্থ সকল কোণের মান সমান হয়] একইভাবে, যেহেতু DC উপচাপ দ্বারা গঠিত দুটি বৃত্তস্থ কোণ হলো ∠CAD ও ∠DBC. ∴ ∠CAD = ∠DBC —- (ii) [একই বৃত্যাংশস্থ সকল কোণের মান সমান হয়] আবার, ∠BAC = ∠CAD [∵ প্রদত্ত আছে AC, ∠BAD -এর সমদ্বিখণ্ডক] সুতরাং, ∠BDC = ∠DBC [(i) ও (ii) নং সমীকরণ ব্যবহার করে পেলাম] এখন, আমরা যা পেলাম, ΔBDC -এর ∠BDC = ∠DBC ∴ BC = CD —– (iii)
আবার, যেহেতু AE সরলরেখাংশের ওপর D বিন্দুতে DE দন্ডায়মান ∴ ∠CDE + ∠ADC = 180° —– (iv) আবার, ∠ADC + ∠ABC = 180° —- (v) [∵ ABCD বৃত্তস্থ চতুর্ভূজ] এখন, (iv) ও (v) নং সমীকরণ দুটি থেকে লেখা যায় – ∠CDE + ∠ADC = ∠ADC + ∠ABC ∴ ∠CDE = ∠ABC —- (vi)
এখন, ΔCED ও ΔABC থেকে পাই – DE = AB [প্রদত্ত আছে] ∠CDE = ∠ABC [(vi) নং সমীকরণ অনুসারে] এবং CD = BC [(iii) নং সমীকরণ অনুসারে] ∴ ΔCED ≅ ΔABC [‘S-A-S’ সর্বসমতার সূত্রানুসারে] সুতরাং, CE = CA [সর্বসম ত্রিভুজের অনুরূপ বাহুদ্বয়] (প্রমানিত) |
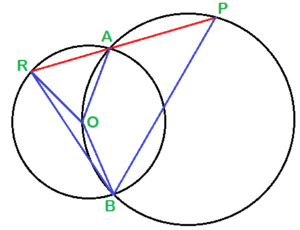
| Q15. দুটি বৃত্তের একটি অপরটির কেন্দ্র O বিন্দুগামী এবং বৃত্ত দুটি পরস্পরকে A ও B বিন্দুতে ছেদ করেছে। A বিন্দুগামী একটি সরলরেখা O বিন্দুগামী বৃত্তকে P বিন্দুতে এবং O কেন্দ্রীয় বৃত্তকে R বিন্দুতে ছেদ করেছে। P, B ও R, B যুক্ত করে, প্রমাণ করি যে PR = PB.
সমাধানঃ
দুটি বৃত্তের মধ্যে একটি বৃত্ত অপর বৃত্তের কেন্দ্র O বিন্দুগামী। বৃত্ত দুটি পরস্পরকে A ও B বিন্দুতে ছেদ করেছে। A বিন্দুগামী একটি সরলরেখা O বিন্দুগামী বৃত্তকে P বিন্দুতে এবং O কেন্দ্রীয় বৃত্তকে R বিন্দুতে ছেদ করেছে। P, B ও R, B যুক্ত করা হলো। প্রমাণ করতে হবে যে, PR = PB অঙ্কনঃ B, R; B, P; B, O; O, R এবং A, O যুক্ত করা হল। প্রমাণঃ যেহেতু AB চাপের উপর ∠AOB হলো কেন্দ্রস্থ কোণ ও ∠ARB হলো বৃত্তস্থ কোণ। ∴ ∠AOB = 2∠ARB
আবার, যেহেতু AOBP বৃত্তস্থ চতুর্ভুজ। ∴ ∠AOB + ∠APB = 180° বা, 2∠ARB + ∠APB = 180° ………(i)
আবার △BPR -এর ∠BRP + ∠RPB + ∠PBR = 180° ………(ii) (i) নং ও (ii) নং থেকে পাই, 2∠ARB + ∠APB = ∠BRP + ∠RPB + ∠PBR বা, 2∠BRP + ∠RPB = ∠BRP + ∠RPB + ∠PBR [∠ARB = ∠BRP; ∠APB = ∠RPB] বা, ∠BRP = ∠PBR সুতরাং, আমরা পেলাম ΔPBR -এর ∠BRP = ∠PBR ∴ PR = PB (প্রমাণিত) |
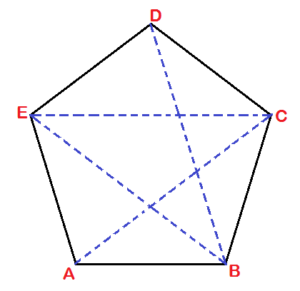
| Q16. প্রমাণ করি যে, একটি সুষম পঞ্চভুজের যে-কোনো চারটি শীর্ষবিন্দু সমবৃত্তস্থ।
সমাধানঃ
ধরি, ABCDE একটি সুষম পঞ্চভুজ। প্রমাণ করতে হবে যে, ABCDE এর যেকোনো চারটি শীর্ষবিন্দু সমবৃত্তস্থ। অঙ্কনঃ A, C; B, D; E, C এবং E, B যুক্ত করা হল। প্রমাণঃ যেহেতু, ABCDE একটি পঞ্চভুজ। ∴ ΔABC, ΔACE ও ΔEBD সমবাহু ত্রিভুজ। অর্থাৎ, ∠BAC = ∠EAC = ∠EDB = 60° এখন, যেহেতু ABDE চতুর্ভুজের ∠BAE + ∠EDB = ∠BAC + ∠EAC + ∠EDB বা, ∠BAE + ∠EDB = 60° + 60° + 60° বা, ∠BAE + ∠EDB = 180° ∴ ABDE বৃত্তস্থ চতুর্ভুজ। ∴ A, B, D, E সমবৃত্তস্থ। সুতরাং, সুষম পঞ্চভুজের যে-কোনো চারটি শীর্ষবিন্দু সমবৃত্তস্থ। (প্রমাণিত) |
| Q17. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.): (i) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB ব্যাস। ABCD বৃত্তস্থ চতুর্ভুজ। ∠ADC = 120° হলে, ∠BAC -এর মান (a) 50° (b) 60° (c) 30° (d) 40° উত্তর : ∠BAC = 30° —- (c)
|
| Q17. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.): (ii) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB ব্যাস। ABCD বৃত্তস্থ চতুর্ভুজ। ∠ABC = 65°, ∠DAC = 40° হলে, ∠BCD -এর মান (a) 75° (b) 105° (c) 115° (d) 80° উত্তর : ∠BCD = 115° —- (c)
|
| Q17. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
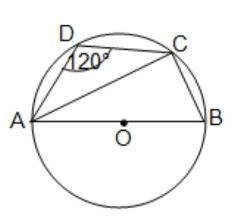
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.): (iii) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB বৃত্তের ব্যাস। ABCD বৃত্তস্থ চতুর্ভুজ যার AB || DC এবং ∠BAC = 25° হলে, ∠DAC -এর মান (a) 50° (b) 25° (c) 130° (d) 40° উত্তর : ∠DAC = 40° —- (d)
|
| Q17. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
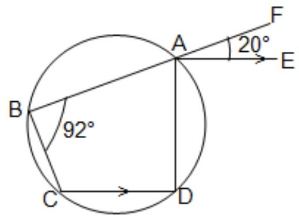
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.): (iv) পাশের চিত্রে ABCD বৃত্তস্থ চতুর্ভুজ। BA -কে F বিন্দু পর্যন্ত বর্ধিত করা হলো। AE || CD, ∠ABC = 92° এবং ∠FAE = 20° হলে, ∠BCD -এর মান (a) 20° (b) 88° (c) 108° (d) 72° উত্তর : ∠BCD = 108° —- (c)
|
| Q17. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)
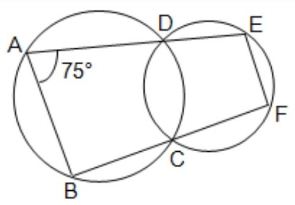
(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.): (v) পাশের চিত্রে দুটি বৃত্ত পরস্পরকে C ও D বিন্দুতে ছেদ করে। D ও C বিন্দুগামী দুটি সরলরেখা একটি বৃত্তকে যথাক্রমে A ও B বিন্দুতে এবং অপর বৃত্তকে E ও F বিন্দুতে ছেদ করে। ∠DAB = 75° হলে, ∠DEF -এর মান (a) 75° (b) 70° (c) 60° (d) 105° উত্তর : ∠DEF = 105° —– (d)
|
| 17 (B) সত্য / মিথ্যা লিখি :
(i) একটি বৃত্তস্থ চতুর্ভুজের বিপরীত কোণ পরস্পর পূরক। উত্তর : বিবৃতিটি মিথ্যা। Note : বৃত্তস্থ চতুর্ভুজের বিপরীত কোনগুলো পরপস্পর সম্পূরক।
17 (B) সত্য / মিথ্যা লিখি : (ii) একটি বৃত্তস্থ চতুর্ভুজের একটি বাহুকে বর্ধিত করলে উৎপন্ন বহিঃস্থ কোণ বিপরীত অন্তঃস্থ কোণের সমান হয়। উত্তর : বিবৃতিটি সত্য। |
Support Me
If you like my work then you can Support me by contributing a small amount which will help me a lot to grow my channel. It’s a request to all of you. You can donate me through phone pay / Paytm/ Gpay on this number 7980608289 or by the link below :
| 17(C) শূন্যস্থান পূরণ করি :
(i) একটি চতুর্ভুজের বিপরীত কোণদ্বয় পরস্পর সম্পূরক হলে চতুর্ভুজের শীর্ষবিন্দুগুলি ________। উত্তর : একটি চতুর্ভুজের বিপরীত কোণদ্বয় পরস্পর সম্পূরক হলে চতুর্ভুজের শীর্ষবিন্দুগুলি সমবৃত্তস্থ।
17(C) শূন্যস্থান পূরণ করি : (ii) একটি বৃত্তস্থ সামান্তরিক একটি __________ চিত্র। উত্তর : একটি বৃত্তস্থ সামান্তরিক একটি আয়তকার চিত্র।
17(C) শূন্যস্থান পূরণ করি : (iii) একটি বর্গাকার চিত্রের শীর্ষবিন্দুগুলি __________। উত্তর : একটি বর্গাকার চিত্রের শীর্ষবিন্দুগুলি সমবৃত্তস্থ। |
| Q18. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) :
(i) পাশের চিত্রে P ও Q কেন্দ্রবিশিষ্ট বৃত্তদুটি B ও C বিন্দুতে ছেদ করেছে। ACD একটি সরলরেখাংশ। ∠ARB = 150°, ∠BQD = x° হলে, x -এর মান নির্ণয় করি। উত্তর : x -এর মান 60°
|
| Q18. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) :
(ii) পাশের চিত্রে দুটি বৃত্ত পরস্পর P ও Q বিন্দুতে ছেদ করে। ∠QAD = 80° এবং ∠PDA = 84° হলে, ∠QBC ও ∠BCP -এর মান নির্ণয় করি। উত্তর : ∠QBC = 100° এবং ∠BCP = 96°
|
| Q18. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) :
(iii) পাশের চিত্রে, ∠BAD = 60°, ∠ABC = 80° হলে, ∠DPC এবং ∠BQC -এর মান নির্ণয় করি। উত্তর : ∠DPC = 40° এবং ∠BQC = 20°
|
| Q18. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) :
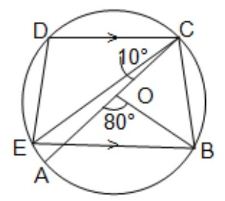
(iv) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AC ব্যাস। ∠AOB = 80° এবং ∠ACE = 10° হলে, ∠BED -এর মান নির্ণয় করি। উত্তর : ∠BED = 100°
|
| Q18. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) :
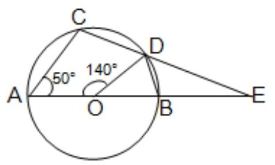
(v) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB বৃত্তের ব্যাস। ∠AOD = 140° এবং ∠CAB = 50° হলে, ∠BED -এর মান নির্ণয় করি। উত্তর : ∠BED = 20°
|
Koshe Dekhi 10 class 10
Support Me
If you like my work then you can Support me by contributing a small amount which will help me a lot to grow my Website. It’s a request to all of you. You can donate me through phone pay / Paytm/ Gpay on this number 7980608289 or by the link below :
and visit Our website : learningscience.co.in
গণিত প্রকাশ (দশম শ্রেণী) সম্পূর্ণ সমাধান
গণিত প্রকাশ (নবম শ্রেণী) সম্পূর্ণ সমাধান
গণিত প্রভা (ষষ্ঠ শ্রেণী) সম্পূর্ণ সমাধান
জীবন বিজ্ঞান (দশম শ্রেণী) (Life Science)
Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10
Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10,Koshe Dekhi 10 class 10
Support Me
If you like my work then you can Support me by contributing a small amount which will help me a lot to grow my channel. It’s a request to all of you. You can donate me through phone pay / Paytm/ Gpay on this number 7980608289 or by the link below :



























Math bengli