Koshe dekhi 18 class 9

1. আমিনাবিবি আজ 2.1 মিটার লম্বা একটি দড়ি দিয়ে তার গােরুটিকে ফাঁকা মাঠে খুঁটির সঙ্গে বাঁধলেন। হিসাব করে দেখি গােরুটি সবথেকে বেশি কতটা জমির ঘাস খেতে পারবে।

সমাধানঃ

গােরুটি সবথেকে বেশি যে জমির ঘাস খেতে পারবে তার ক্ষেত্রফল 2.1 মিটার ব্যাসার্ধ বিশিষ্ট বৃত্তের ক্ষেত্রফলের সমান।

∴ বৃত্তের ক্ষেত্রফল

$=\pi r^{2}$ বর্গ মিটার

$=\frac{22}{7}\times \left ( 2.1 \right )^{2}$

$=\frac{22}{7}\times \frac{21}{10}\times \frac{21}{10}$

= 13.86 বর্গ মিটার

উত্তরঃ গােরুটি সবথেকে বেশি 13.86 বর্গ মিটার জমির ঘাস খেতে পারবে।

2. সুহানা একটি বৃত্ত আঁকবে যার পরিধি হবে 35.2 সেমি। হিসাব করে দেখি সুহানা যে বৃত্ত আঁকবে তার ব্যাসার্ধের দৈর্ঘ্য কত নেবে এবং বৃত্তাকার ক্ষেত্রের ক্ষেত্রফল কত হবে ?

সমাধানঃ

সুহানার অঙ্কিত বৃত্তের পরিধি 35.2 সেমি।

ধরি, সুহানার অঙ্কিত বৃত্তের ব্যাসার্ধের দৈর্ঘ্য r সেমি।

প্রশ্নানুসারে,

$2\pi r=35.2$

বা, $2\times \frac{22}{7}\times r=\frac{352}{10}$

বা, $r=\frac{352\times 7}{10\times 2\times 22}$

∴ r = 5.6

বৃত্তটির ক্ষেত্রফল

$=\pi r^{2}$ বর্গ সেমি

$=\frac{22}{7}\times \left ( 5.6 \right )^{2}$

$=\frac{22}{7}\times \frac{56}{10}\times \frac{56}{10}$

= 98.56 বর্গ সেমি

উত্তরঃ সুহানার অঙ্কিত বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 5.6 সেমি এবং বৃত্তাকার ক্ষেত্রের ক্ষেত্রফল 98.56 বর্গ সেমি।

3. রেখার দিদিমা একটি গােলাকার টেবিলের ঢাকনা তৈরি করেছেন যার ক্ষেত্রফল 5544 বর্গ সেমি.৷ তিনি এই টেবিলের ঢাকনার চারিদিকে রঙিন ফিতে লাগাতে চান। হিসাব করে দেখি দিদিমাকে কত দৈর্ঘ্যের রঙিন ফিতে কিনতে হবে।

সমাধানঃ

ধরি, গোলাকার টেবিলের ঢাকনার ব্যাসার্ধ = r সেমি.৷

প্রশ্নানুসারে,

$\pi r^{2}=5544$

বা, $\frac{22}{7}\times r^{2}=5544$

বা, $r^{2}=5544\times \frac{7}{22}$

বা, $r^{2}=252\times 7$

$\therefore r=42$ সেমি.

রেখার দিদিমাকে গোলাকার টেবিলের পরিধির সমান রঙিন ফিতে লাগাতে হবে।

গোলাকার টেবিলের পরিধি

$=2\pi r$

$=2\times \frac{22}{7}\times 42$

= 264 সেমি.

উত্তরঃ দিদিমাকে 264 সেমি. দৈর্ঘ্যের রঙিন ফিতে কিনতে হবে।

4. আমাদের পাড়ার বৃত্তাকার খেলার মাঠটি বেড়া দিয়ে ঘিরতে প্রতি মিটার 21 টাকা হিসাবে 924 টাকা খরচ হয়েছে। মাঠটি ত্রিপল দিয়ে ঢেকে দেওয়ার জন্য কত বর্গমিটার ত্রিপল কিনতে হবে হিসাব করে লিখি।

সমাধানঃ

ধরি, মাঠটির ব্যাসার্ধ r মিটার।

মাঠটির পরিধি

$=\frac{924}{21}$

= 44 মিটার

প্রশ্নানুসারে,

$2\pi r=44$

বা, $2\times \frac{22}{7}\times r=44$

বা, $r=\frac{44\times 7}{2\times 22}$

∴ r = 7

মাঠটির ক্ষেত্রফল

$=\pi r^{2}$ বর্গ মিটার

$=\frac{22}{7}\times \left ( 7 \right )^{2}$

= 154 বর্গ মিটার

উত্তরঃ মাঠটি ত্রিপল দিয়ে ঢেকে দেওয়ার জন্য 154 বর্গ মিটার ত্রিপল কিনতে হবে।

5. ফারুক একটি বৃত্ত আঁকবে যার ক্ষেত্রের ক্ষেত্রফল হবে 616 বর্গসেমি.৷ হিসাব করে দেখি ফারুক যে বৃত্ত আঁকবে তার ব্যাসার্ধের দৈর্ঘ্য কত নেবে এবং বৃত্তটির পরিধি কত পাবে।

সমাধানঃ

ধরি, ফারুকের অঙ্কিত বৃত্তের ব্যাসার্ধ r সেমি.।

ফারুকের অঙ্কিত বৃত্তের ক্ষেত্রফল 616 বর্গসেমি.৷

প্রশ্নানুসারে,

$\pi r^{2}=616$

বা, $\frac{22}{7}\times r^{2}=616$

বা, $r^{2}=616\times \frac{7}{22}$

বা, $r^{2}=28\times 7$

∴ r = 14 সেমি.

বৃত্তটির পরিধি

$=2\pi r$

$=2\times \frac{22}{7}\times 14$

= 88 সেমি.

উত্তরঃ ফারুক যে বৃত্ত আঁকবে তার ব্যাসার্ধের দৈর্ঘ্য 14 সেমি. এবং বৃত্তটির পরিধি 88 সেমি.।

6. পলাশ ও পিয়ালী দুটি বৃত্ত এঁকেছে যাদের ব্যাসার্ধের দৈর্ঘ্য অনুপাত 4 : 5; হিসাব করে দুজনের আঁকা বৃত্তাকার ক্ষেত্র দুটির ক্ষেত্রফলের অনুপাত লিখি।

সমাধানঃ

ধরি, পলাশ ও পিয়ালীর অঙ্কিত বৃত্ত দুটির ব্যাসার্ধের দৈর্ঘ্য যথাক্রমে 4r একক এবং 5r একক।

∴ পলাশ ও পিয়ালীর অঙ্কিত বৃত্ত দুটির ক্ষেত্রফলের অনুপাত

$=\pi \times \left ( 4r \right )^{2}:\pi \times \left ( 5r \right )^{2}$

= 16 : 25

উত্তরঃ পলাশ ও পিয়ালীর অঙ্কিত বৃত্ত দুটির ক্ষেত্রফলের অনুপাত 16 : 25

7. সুমিত ও রেবা একই দৈর্ঘ্যের দুটি তামার তার এনেছে। সুমিত ওই তারটি বেঁকিয়ে আয়তাকার চিত্র তৈরি করেছে যার দৈর্ঘ্য 48 সেমি., এবং প্রস্থ 40 সেমি.৷ কিন্তু রেবা একই দৈর্ঘ্যের তামার তারটি বেঁকিয়ে বৃত্ত তৈরি করল৷ হিসাব করে দেখি সুমিতের তৈরি আয়তাকার চিত্র এবং রেবার তৈরি বৃত্তের মধ্যে কোনটি বেশি জায়গা জুড়ে থাকবে।

সমাধানঃ

সুমিতের তৈরি আয়তাকার চিত্রের পরিসীমা

$=2\times \left ( 48+40 \right )$

= 176 সেমি.

যেহেতু দুটি তারের দৈর্ঘ্য সমান, তাই রেবার তৈরি বৃত্তাকার চিত্রের পরিসীমা 176 সেমি. হবে।

ধরি, বৃত্তের ব্যাসার্ধ = r সেমি.

প্রশ্নানুসারে,

$2\pi r=176$

বা, $2\times \frac{22}{7}\times r=176$

বা, $r=\frac{176\times 7}{2\times 22}$

∴ r = 28 সেমি.

সুমিতের তৈরি আয়তাকার চিত্রের ক্ষেত্রফল

= 48 × 40

= 1920 বর্গ সেমি.

রেবার তৈরি বৃত্তাকার চিত্রের ক্ষেত্রফল

$=\pi r^{2}$

64 বর্গ সেমি.

উত্তরঃ সুমিতের তৈরি আয়তাকার চিত্র এবং রেবার তৈরি বৃত্তের মধ্যে রেবার তৈরি বৃত্তাকার চিত্রটি বেশি জায়গা জুড়ে থাকবে।

8. পাইওনিয়ার অ্যাথলেটিক ক্লাবের আয়তাকার মাঠের মাঝখানে একটি বৃত্তাকার জলাশয় আছে যার ব্যাসার্ধের দৈর্ঘ্য 14 মিটার। আয়তাকার মাঠের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 60 মিটার ও 42 মিটার। জলাশয় বাদে আয়তাকার মাঠের বাকি জায়গায় ঘাস লাগাতে প্রতি বর্গমিটার 75 টাকা হিসাবে কত খরচ হবে হিসাব করে দেখি।

বৃত্তের ক্ষেত্রফল

সমাধানঃ

প্রদত্ত,

আয়তাকার মাঠের দৈর্ঘ্য ও প্রস্থ যথাক্রমে 60 মিটার ও 42 মিটার।

∴ আয়তাকার মাঠের ক্ষেত্রফল

= দৈর্ঘ্য × প্রস্থ

= 60 × 42

= 2520 বর্গমিটার

আয়তাকার মাঠের মাঝে অবস্থিত বৃত্তের ব্যাসার্ধ (r) = 14 মিটার।

∴ বৃত্তটির ক্ষেত্রফল

$=\pi r^{2}$ বর্গমিটার

$=\frac{22}{7}\times \left ( 14 \right )^{2}$

= 616 বর্গমিটার

জলাশয় বাদে আয়তাকার মাঠের ক্ষেত্রফল

= (2520 − 616) বর্গমিটার

= 1904 বর্গমিটার

প্রতি বর্গমিটার 75 টাকা হিসাবে ঘাস লাগাতে খরচ হবে

= 1904 × 75

= 142800 টাকা

উত্তরঃ জলাশয় বাদে আয়তাকার মাঠের বাকি জায়গায় ঘাস লাগাতে প্রতি বর্গমিটার 75 টাকা হিসাবে 142800 টাকা খরচ হবে।

9. ইটালগাছা ফ্রেন্ডস এসােসিয়েশন ক্লাবের বৃত্তাকার পার্কের বাইরের দিকে পরিধি বরাবর একটি 7 মিটার চওড়া রাস্তা আছে৷ বৃত্তাকার পার্কের পরিধি 352 মিটার হলে রাস্তাটির ক্ষেত্রফল হিসাব করে লিখি। প্রতি বর্গমিটার 20 টাকা হিসাবে রাস্তাটি বাঁধতে কত টাকা খরচ হবে হিসাব করে লিখি।

সমাধানঃ

ধরি, বৃত্তাকার পার্কের ব্যাসার্ধ = r মিটার।

প্রশ্নানুসারে,

$2\pi r=352$

বা, $2\times \frac{22}{7}\times r=352$

বা, $r=352\times \frac{7}{22\times 2}$

∴ r = 56 মিটার

∴ বৃত্তাকার পার্কের ব্যাসার্ধ 56 মিটার।

এখন, বৃত্তাকার পার্কের বাইরের দিকে পরিধি বরাবর একটি 7 মিটার চওড়া রাস্তা থাকলে, রাস্তাসহ পার্কটির ব্যাসার্ধ

= (56 + 7) মিটার

= 63 মিটার।

রাস্তাসহ পার্কটির ক্ষেত্রফল

$=\pi \times \left ( 63 \right )^{2}$

$=\frac{22}{7}\times 63\times 63$

= 12474 বর্গমিটার

রাস্তাবাদে পার্কটির ক্ষেত্রফল

$=\pi \times \left ( 56 \right )^{2}$

$=\frac{22}{7}\times 56\times 56$

= 9856 বর্গমিটার

∴ রাস্তার ক্ষেত্রফল

= (12474 − 9856)বর্গমিটার

= 2618 বর্গমিটার

প্রতি বর্গমিটার 20 টাকা হিসাবে রাস্তাটি বাঁধতে খরচ হবে

= 2618 × 20

= 52360 টাকা

উত্তরঃ (i) রাস্তাটির ক্ষেত্রফল 2618 বর্গমিটার

(ii) প্রতি বর্গমিটার 20 টাকা হিসাবে রাস্তাটি বাঁধতে 52360 টাকা খরচ হবে।

10. আনােয়ারাবিবি তার অর্ধবৃত্তাকার জমির চারদিকে প্রতি মিটার 18.50 টাকা হিসাবে বেড়া দিতে 2664 টাকা খরচ করেছেন। তিনি যদি তার ওই অর্ধবৃত্তাকার জমি প্রতি বর্গমিটার 32 টাকা হিসাবে চাষ করান। তাহলে মােট কত টাকা খরচ করবেন হিসাব করে লিখি।

সমাধানঃ

আনােয়ারাবিবির অর্ধবৃত্তাকার জমির পরিধি

$=\frac{2664}{18.50}$ মিটার

= 144 মিটার

ধরি, অর্ধবৃত্তাকার জমির ব্যাসার্ধ r মিটার।

প্রশ্নানুসারে,

$\pi r+2r=144$

বা, $r\left ( \pi +2 \right )=144$

বা, $r\left ( \frac{22}{7}+2 \right )=144$

বা, $r\times \left (\frac{22+14}{7} \right )=144$

বা, $r=144\times \frac{7}{36}$

∴ r = 28

অর্ধবৃত্তাকার জমির ক্ষেত্রফল

$=\frac{\pi r^{2}}{2}$

$=\frac{\frac{22}{7}\times 28\times 28}{2}$

= 1232

প্রতি বর্গমিটার 32 টাকা হিসাবে চাষ করলে খরচ হবে

= 1232 × 32 টাকা

= 39424 টাকা

উত্তরঃ আনােয়ারাবিবি চাষ করতে মােট 39424 টাকা খরচ করবেন।

11. আজ আমার বন্ধু রজত একই বেগে দৌড়ে স্কুলের বৃত্তাকার মাঠটি যে সময়ে একবার প্রদক্ষিণ করল একই বেগে মাঠের ব্যাস বরাবর দৌড়তে 30 সেকেণ্ড কম সময় নিল। তার গতিবেগ 9 মিটার/ সেকেণ্ড হলে স্কুলের মাঠের ক্ষেত্রফল হিসাব করে লিখি।

সমাধানঃ

রজত 1 সেকেন্ডে যায় 9 মিটার

∴ 30 সেকেন্ডে যায় = 9 × 30 ⇒ 270 মিটার

∴ স্কুলের মাঠটির ব্যাস পরিধি অপেক্ষা 270 মিটার ছোট।

ধরি, মাঠটির ব্যাসার্ধ r মিটার।

প্রশ্নানুসারে,

$\small 2\pi r-2r=270$

বা, $\small 2r\left ( \pi -1 \right )=270$

বা, $\small 2r\left ( \frac{22}{7}-1 \right )=270$

বা, $\small 2r\left ( \frac{22-7}{7} \right )=270$

বা, $\small 2r\times \frac{15}{7}=270$

বা, $\small r=270\times \frac{7}{15\times 2}$

∴ $\small r=9\times 7\Rightarrow 63$ মিটার

∴ স্কুলের মাঠের ক্ষেত্রফল

$=\pi \times \left ( 63 \right )^{2}$

$=\frac{22}{7}\times 63\times 63$

= 12474 বর্গমিটার

উত্তরঃ স্কুলের মাঠের ক্ষেত্রফল 12474 বর্গমিটার।

12. বকুলতলার বৃত্তাকার মাঠের বাইরের চারদিকে একটি সমপরিসরের রাস্তা আছে। রাস্তাটির বাইরের সীমারেখার দৈর্ঘ্য ভিতরের সীমারেখার দৈর্ঘ্য অপেক্ষা 132 মিটার বেশি। পথটির ক্ষেত্রফল 14190 বর্গ মি. হলে বৃত্তাকার মাঠটির ক্ষেত্রফল হিসাব করে লিখি।

সমাধানঃ

ধরি, বৃত্তাকার মাঠটির ব্যাসার্ধ r মিটার এবং রাস্তাসহ বৃত্তাকার মাঠটির ব্যাসার্ধ R মিটার।

প্রশ্নানুসারে,

$2\pi R-2\pi r=132$

বা, $2\pi \left ( R-r \right )=132$

বা, $2\times \frac{22}{7}\left ( R-r \right )=132$

বা, $R-r=132\times \frac{7}{22\times 2}$

বা, R − r = 21 ……(i)

আবার,

$\pi R^{2}-\pi r^{2}=14190$

বা, $\pi \left (R^{2}-r^{2} \right )=14190$

বা, $\frac{22}{7}\times \left ( R+r \right )\left ( R-r \right )=14190$

বা, $\frac{22}{7}\times \left ( R+r \right )\times 21=14190$

বা, $\left ( R+r \right )=14190\times \frac{7}{21\times 22}$

বা, R + r = 215 ……(ii)

(i) + (ii) করে পাই,

R − r + R + r= 21 + 215

বা, 2R = 236

বা, $R=\frac{236}{2}$

∴ R = 118

(ii) নং সমীকরণে R এর মান বসিয়ে পাই,

r = 215 − 118

∴ r = 97

∴ বৃত্তাকার মাঠটির ক্ষেত্রফল

$=\frac{22}{7}\times \left ( 97 \right )^{2}$

$=\frac{206998}{7}$

$=29571\frac{1}{7}$ বর্গমিটার

উত্তরঃ বৃত্তাকার মাঠটির ক্ষেত্রফল ${\color{DarkGreen} 29571\frac{1}{7}}$ বর্গমিটার

13. নীচের ছবির রেখাঙ্কিত অঞ্চলের ক্ষেত্রফল হিসাব করে লিখি-

(i) 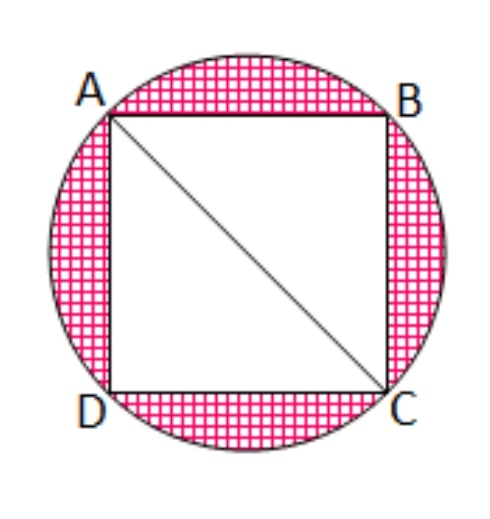বৃত্তের ক্ষেত্রফল

ABCD একটি বর্গক্ষেত্র। বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 7 সেমি।

সমাধানঃ

প্রদত্ত, বৃত্তের ব্যাসার্ধের দৈর্ঘ্য (r) = 7 সেমি।

∴ বৃত্তটির ব্যাস = 2 × ব্যাসার্ধ = 2 × 7 = 14 সেমি

∴ বৃত্তটির ক্ষেত্রফল

$=\pi \times \left ( 7 \right )^{2}$

$=\frac{22}{7}\times 7\times 7$

= 154 বর্গসেমি.

চিত্রানুযায়ী,

বৃত্তের ব্যাস = বর্গক্ষেত্রের কর্ণ $\left ( a\sqrt{2} \right )=14$ সেমি [ধরি, বর্গক্ষেত্রের বাহুর দৈর্ঘ্য = a সেমি]

$\therefore a\sqrt{2}=14$

বা, $a=\frac{14}{\sqrt{2}}$

$\therefore a=7\sqrt{2}$

∴ বর্গক্ষেত্রের ক্ষেত্রফল

$=a^{2}$

$=\left ( 7\sqrt{2} \right )^{2}$

$=7\sqrt{2}\times 7\sqrt{2}$

= 98 বর্গসেমি.

∴ রেখাঙ্কিত অঞ্চলের ক্ষেত্রফল

= (154 − 98) বর্গসেমি.

= 56 বর্গসেমি.

উত্তরঃ রেখাঙ্কিত অঞ্চলের ক্ষেত্রফল 56 বর্গসেমি.

13. নীচের ছবির রেখাঙ্কিত অঞ্চলের ক্ষেত্রফল হিসাব করে লিখি-

(ii) বৃত্তের ক্ষেত্রফল

প্রতিটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 3.5 সেমি। চারটি বৃত্তের কেন্দ্র যথাক্রমে A,B,C,D

সমাধানঃ

প্রতিটি বৃত্তের ক্ষেত্রফল

$=\pi \times \left ( 3.5 \right )^{2}$

$=\frac{22}{7}\times \frac{35}{10}\times \frac{35}{10}$

= 38.5 বর্গসেমি.

∴ 4টি বৃত্তের মোট ক্ষেত্রফল

= 4 × 38.5

= 154 বর্গসেমি.

ABCD বর্গক্ষেত্রটি প্রতিটি বৃত্তের $\frac{1}{4}$ অংশ দখল করে আছে।

চিত্রে 4 টি বৃত্ত আছে।

∴ ABCD বর্গক্ষেত্রটি মোট $4\times \frac{1}{4}=1$ টি বৃত্তের সমান স্থান দখল করে আছে।

অর্থাৎ,

ABCD বর্গক্ষেত্রটির ক্ষেত্রফল

= একটি বৃত্তের ক্ষেত্রফল

= 38.5 বর্গসেমি.

∴ 4 টি বৃত্তের রেখাঙ্কিত অঞ্চলের ক্ষেত্রফল

= 4টি বৃত্তের মোট ক্ষেত্রফল − ABCD বর্গক্ষেত্রটির ক্ষেত্রফল

= (154 − 38.5) বর্গসেমি.

= 115.5 বর্গসেমি.

উত্তরঃ রেখাঙ্কিত অঞ্চলের ক্ষেত্রফল 115.5 বর্গসেমি.

14. দীনেশ তাদের শ্রেণির কতজন কোন খেলা খেলতে ভালােবাসে তার একটা পাই-চিত্র তৈরি করেছে। সে বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 3.5 সেমি. নিয়েছে। হিসাব করে প্রতিটি বৃত্তকলার পরিসীমা ও ক্ষেত্রফল লিখি।

সমাধানঃ

ধরা যাক, দীনেশের শ্রেণীতে মোট 60 জন ছাত্র আছে। এই 60 জন ছাত্রের মধ্যে কতজন ছাত্র কোন খেলা পছন্দ করে তার একটি সারণি নিচে দেওয়া হলো –

খেলার নাম	ছাত্র সংখ্যা (জন)
ক্রিকেট	26
ফুটবল	20
টেনিস	8
ভলিবল	6
মোট	= 60

পাই চিত্র গঠনের তথ্য
মোট খেলোয়াড়ের সংখ্যা = 60 জন
ক্রিকেট খেলতে ভালোবাসে এমন ছাত্রের সংখ্যা = 26 জন

∴ পাই চিত্রে ক্রিকেট খেলা যে বৃত্তকলা সৃষ্টি করে তা বৃত্তের কেন্দ্রে $\small \left (\frac{26}{60}\times 360 \right )^{\circ}$ অর্থ্যাৎ 156° কোণ উৎপন্ন করে।

একইভাবে, পাই চিত্রে ফুটবল খেলা যে বৃত্তকলা সৃষ্টি করে তা বৃত্তের কেন্দ্রে $\small \left (\frac{20}{60}\times 360 \right )^{\circ}$ অর্থ্যাৎ 120° কোণ উৎপন্ন করে।

পাই চিত্রে টেনিস খেলা যে বৃত্তকলা সৃষ্টি করে তা বৃত্তের কেন্দ্রে $\small \left (\frac{8}{60}\times 360 \right )^{\circ}$ অর্থ্যাৎ 48° কোণ উৎপন্ন করে।

পাই চিত্রে ভলিবল খেলা যে বৃত্তকলা সৃষ্টি করে তা বৃত্তের কেন্দ্রে $\small \left (\frac{6}{60}\times 360 \right )^{\circ}$ অর্থ্যাৎ 36° কোণ উৎপন্ন করে।

পরিসীমা :

156° কেন্দ্রীয় কোণ সম্পন্ন বৃত্তকলার পরিসীমা,

$\small =\frac{2\pi r}{360^{\circ}}\times 156^{\circ}$

এখন, বৃত্তের ব্যাসার্ধ (r) = 3.5 সেমি. (দেওয়া আছে) বসিয়ে পাই,

$\small =\frac{2\pi \times 3.5}{360^{\circ}}\times 156^{\circ}$ সেমি.

$\small =\frac{91\pi}{30}$ সেমি. (উত্তর)

120° কেন্দ্রীয় কোণ সম্পন্ন বৃত্তকলার পরিসীমা,

$\small =\frac{2\pi r}{360^{\circ}}\times 120^{\circ}$

এখন, বৃত্তের ব্যাসার্ধ (r) = 3.5 সেমি. (দেওয়া আছে) বসিয়ে পাই,

$\small =\frac{2\pi \times 3.5}{360^{\circ}}\times 120^{\circ}$ সেমি.

$\small =\frac{7\pi}{3}$ সেমি. (উত্তর)

48° কেন্দ্রীয় কোণ সম্পন্ন বৃত্তকলার পরিসীমা,

$\small =\frac{2\pi r}{360^{\circ}}\times 48^{\circ}$

এখন, বৃত্তের ব্যাসার্ধ (r) = 3.5 সেমি. (দেওয়া আছে) বসিয়ে পাই,

$\small =\frac{2\pi \times 3.5}{360^{\circ}}\times 48^{\circ}$ সেমি.

$\small =\frac{14\pi}{15}$ সেমি. (উত্তর)

36° কেন্দ্রীয় কোণ সম্পন্ন বৃত্তকলার পরিসীমা,

$\small =\frac{2\pi r}{360^{\circ}}\times 36^{\circ}$

এখন, বৃত্তের ব্যাসার্ধ (r) = 3.5 সেমি. (দেওয়া আছে) বসিয়ে পাই,

$\small =\frac{2\pi \times 3.5}{360^{\circ}}\times 36^{\circ}$ সেমি.

$\small =\frac{7\pi}{10}$ সেমি. (উত্তর)

ক্ষেত্রফল :

156° কেন্দ্রীয় কোণ সম্পন্ন বৃত্তকলার ক্ষেত্রফল,

$\small =\frac{\pi r^{2}}{360^{\circ}}\times 156^{\circ}$

এখন, বৃত্তের ব্যাসার্ধ (r) = 3.5 সেমি. (দেওয়া আছে) বসিয়ে পাই,

$\small =\frac{\pi \times 3.5^{2}}{360^{\circ}}\times 156^{\circ}$ বর্গ সেমি.

$\small =\frac{637\pi}{120}$ বর্গ সেমি. (উত্তর)

120° কেন্দ্রীয় কোণ সম্পন্ন বৃত্তকলার ক্ষেত্রফল,

$\small =\frac{\pi r^{2}}{360^{\circ}}\times 120^{\circ}$

এখন, বৃত্তের ব্যাসার্ধ (r) = 3.5 সেমি. (দেওয়া আছে) বসিয়ে পাই,

$\small =\frac{\pi \times 3.5^{2}}{360^{\circ}}\times 120^{\circ}$ বর্গ সেমি.

$\small =\frac{49\pi}{12}$ বর্গ সেমি. (উত্তর)

48° কেন্দ্রীয় কোণ সম্পন্ন বৃত্তকলার ক্ষেত্রফল,

$\small =\frac{\pi r^{2}}{360^{\circ}}\times 48^{\circ}$

এখন, বৃত্তের ব্যাসার্ধ (r) = 3.5 সেমি. (দেওয়া আছে) বসিয়ে পাই,

$\small =\frac{\pi \times 3.5^{2}}{360^{\circ}}\times 48^{\circ}$ বর্গ সেমি.

$\small =\frac{49\pi}{30}$ বর্গ সেমি. (উত্তর)

36° কেন্দ্রীয় কোণ সম্পন্ন বৃত্তকলার ক্ষেত্রফল,

$\small =\frac{\pi r^{2}}{360^{\circ}}\times 36^{\circ}$

এখন, বৃত্তের ব্যাসার্ধ (r) = 3.5 সেমি. (দেওয়া আছে) বসিয়ে পাই,

$\small =\frac{\pi \times 3.5^{2}}{360^{\circ}}\times 36^{\circ}$ বর্গ সেমি.

$\small =\frac{49\pi}{40}$ বর্গ সেমি. (উত্তর)

15. নীতু একটি বর্গক্ষেত্র ABCD এঁকেছে যার প্রতিটি বাহুর দৈর্ঘ্য 12 সেমি.। আমার বােন পাশের ছবির মতাে A, B, C ও D বিন্দুকে কেন্দ্র করে 6 সেমি. দৈর্ঘ্যের ব্যাসার্ধের চারটি বৃত্তচাপ এঁকেছে এবং কিছু জায়গায় নকশা এঁকেছে৷

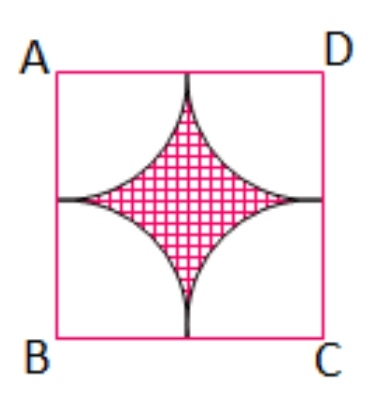
বৃত্তের ক্ষেত্রফল

হিসাব করে নকশা আঁকা ক্ষেত্রের পরিসীমা ও ক্ষেত্রফল লিখি।

সমাধানঃ

বর্গক্ষেত্র ABCD এর প্রতিটি বাহুর দৈর্ঘ্য (a) = 12 সেমি.।

4 টি বৃত্তচাপ মিলিত হয়ে 1 টি সম্পূর্ণ বৃত্ত গঠন করে।

প্রতিটি বৃত্তের বৃত্তচাপের দৈর্ঘ্য

$=\frac{1}{4}\times 2\pi r$

$=\frac{1}{4}\times 2\times \frac{22}{7}\times 6$

$=\frac{1}{4}\times \frac{264}{7}$ সেমি

∴ নকশা আঁকা ক্ষেত্রের পরিসীমা

$=4\times \frac{1}{4}\times \frac{264}{7}$

$=\frac{264}{7}$

$=37\frac{5}{7}$ সেমি.

∴ বর্গক্ষেত্রটির ক্ষেত্রফল

$=\left ( a \right )^{2}$

$=\left ( 12 \right )^{2}$

= 144 বর্গসেমি.

নকশা আঁকা ছাড়া বাকি অংশের ক্ষেত্রফল

$=\pi \times \left ( 6 \right )^{2}$

$=\frac{22}{7}\times 36$

$=\frac{792}{7}$ বর্গ সেমি

∴ নকশা আঁকা ক্ষেত্রের ক্ষেত্রফল

$=144-\frac{792}{7}$

$=\frac{1008-792}{7}$

$=\frac{216}{7}$

$=30\frac{6}{7}$ বর্গ সেমি

উত্তরঃ নকশা আঁকা ক্ষেত্রের পরিসীমা ${\color{DarkGreen} 37\frac{5}{7}}$ সেমি. ও ক্ষেত্রফল ${\color{DarkGreen} 30\frac{6}{7}}$ বর্গ সেমি।

16. একটি বৃত্তাকার মাঠের ক্ষেত্রফল 154 বর্গ সেমি.। বৃত্তাকার মাঠটির পরিলিখিত বর্গক্ষেত্রের পরিসীমা ও ক্ষেত্রফল হিসাব করে লিখি। যদি বর্গক্ষেত্রটি বৃত্তাকার মাঠের অন্তলিখিত হতাে তাহলে বর্গক্ষেত্রটির পরিসীমা ও ক্ষেত্রফল কত হতাে তা হিসাব করে লিখি।

সমাধানঃ

ধরি, বৃত্তাকার মাঠের ব্যাসার্ধ r সেমি. ও বর্গক্ষেত্রের বাহুর দৈর্ঘ্য a সেমি.।

প্রশ্নানুসারে,

$\pi r^{2}=154$

বা, $\frac{22}{7}\times r^{2}=154$

বা, $r^{2}=154\times \frac{7}{22}$

বা, $r^{2}=7\times 7$

∴ r = 7 সেমি.

বৃত্তাকার মাঠটির পরিলিখিত বর্গক্ষেত্রের বাহুর দৈর্ঘ্য (a) = বৃত্তাকার মাঠটির ব্যাস (2r) = 2 × 7 = 14 সেমি.

∴ বর্গক্ষেত্রটির পরিসীমা

= 4a

= 4 × 14

= 56 সেমি.

ও ক্ষেত্রফল

$=a^{2}$

$=\left ( 14 \right )^{2}$

= 196 বর্গ সেমি

আবার,যদি বর্গক্ষেত্রটি বৃত্তাকার মাঠের অন্তলিখিত হতাে তবে

বৃত্তাকার মাঠটির অন্তলিখিত বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য $\left ( a\sqrt{2} \right )$ = বৃত্তাকার মাঠটির ব্যাস (2r) = 2 × 7 = 14 সেমি. হতো।

$a\sqrt{2}=14$

বা, $a=\frac{14}{\sqrt{2}}$

$\therefore a=7\sqrt{2}$ সেমি.

∴ বর্গক্ষেত্রটির পরিসীমা

= 4a

$=4\times 7\sqrt{2}$

$=28\sqrt{2}$ সেমি.

ও ক্ষেত্রফল

$=a^{2}$

$=\left ( 7\sqrt{2} \right )^{2}$

= 98 বর্গ সেমি

উত্তরঃ (i) বৃত্তাকার মাঠটির পরিলিখিত বর্গক্ষেত্রের পরিসীমা 56 সেমি. ও ক্ষেত্রফল 196 বর্গ সেমি।

(ii) বৃত্তাকার মাঠের অন্তলিখিত হতাে তাহলে বর্গক্ষেত্রটির পরিসীমা ${\color{DarkGreen} 28\sqrt{2}}$ সেমি. ও ক্ষেত্রফল 98 বর্গ সেমি।

17. নীচের বৃত্তকলাগুলির রেখাঙ্কিত অঞ্চলের পরিসীমা ও ক্ষেত্রফল লিখি –

(i) বৃত্তের ক্ষেত্রফল

সমাধানঃ

সমকোণী ত্রিভুজের অতিভূজ AB এর দৈর্ঘ্য

$=\sqrt{\left ( 12 \right )^{2}+\left ( 12 \right )^{2}}$

$=\sqrt{2\left ( 12 \right )^{2}}$

$=12\sqrt{2}$

= 12 × 1.432

= 16.968 সেমি.

AB বৃত্তচাপের দৈর্ঘ্য

$=\frac{1}{4}\times 2\pi r$ [ যেহেতু,সম্পূর্ণ বৃত্তের ${\color{Blue} \frac{1}{4}}$ অংশ ]

$=\frac{1}{4}\times 2\times \frac{22}{7}\times 12$

= 18.857 সেমি.

∴ রেখাঙ্কিত অঞ্চলের পরিসীমা

= অতিভূজ AB এর দৈর্ঘ্য + AB বৃত্তচাপের দৈর্ঘ্য

= 16.968 + 18.857

= 35.83 সেমি. (প্রায়)

সমগ্র অংশের ক্ষেত্রফল

$=\frac{1}{4}\pi r^{2}$

$=\frac{1}{4}\times \frac{22}{7}\times \left ( 12 \right )^{2}$

$=\frac{792}{7}$ বর্গসেমি.

সমকোণী ত্রিভুজের ক্ষেত্রফল

$=\frac{1}{2}$ × ভূমি × উচ্চতা

$=\frac{1}{2}\times 12\times 12$

= 72 বর্গসেমি.

∴ রেখাঙ্কিত অঞ্চলের ক্ষেত্রফল

$=\left (\frac{792}{7}-72 \right )$ বর্গসেমি.

$=\frac{288}{7}$

$=41\frac{1}{7}$ বর্গসেমি.

উত্তরঃ রেখাঙ্কিত অঞ্চলের পরিসীমা 35.83 সেমি. (প্রায়) ও ক্ষেত্রফল ${\color{DarkGreen} 41\frac{1}{7}}$ বর্গসেমি. ।

17. নীচের বৃত্তকলাগুলির রেখাঙ্কিত অঞ্চলের পরিসীমা ও ক্ষেত্রফল লিখি –

(ii) বৃত্তের ক্ষেত্রফল

সমাধানঃ

AC বৃত্তচাপের দৈর্ঘ্য

$=\frac{60}{360}\times 2\pi r$ [ যেহেতু,সম্পূর্ণ বৃত্তের ${\color{Blue} \frac{1}{6}}$ অংশ ]

$=\frac{1}{6}\times 2\times \frac{22}{7}\times 42$

= 44 সেমি.

∴ রেখাঙ্কিত অঞ্চলের পরিসীমা

= AC বাহুর দৈর্ঘ্য + AC বৃত্তচাপের দৈর্ঘ্য

= 42 + 44

= 86 সেমি.

সমগ্র অংশের ক্ষেত্রফল

$=\frac{60}{360}\pi r^{2}$

$=\frac{1}{6}\times \frac{22}{7}\times \left ( 42 \right )^{2}$

=924 বর্গসেমি.

ABC সমবাহু ত্রিভুজের ক্ষেত্রফল

$=\frac{\sqrt{3}}{4}$ × বাহু × বাহু

$=\frac{\sqrt{3}}{4}\times 42\times 42$

= 763.812 বর্গসেমি.

∴ রেখাঙ্কিত অঞ্চলের ক্ষেত্রফল

= (924 − 763.812) বর্গসেমি.

= 160.188 বর্গসেমি.

উত্তরঃ রেখাঙ্কিত অঞ্চলের পরিসীমা 86 সেমি. ও ক্ষেত্রফল 160.188 বর্গসেমি.

18. লীনা মেলা থেকে একটি বালা কিনে হাতে পরেছে৷ বালাটিতে 269.5 বর্গ সেমি. ধাতু আছে। বালাটির বহির্ব্যাসের দৈর্ঘ্য 28 সেমি. হলে অন্তর্ব্যাসের দৈর্ঘ্য কত হিসাব করে লিখি।

সমাধানঃ

ধরি, অন্তর্ব্যাসার্ধের দৈর্ঘ্য r সেমি.

বালাটির বহির্ব্যাসের দৈর্ঘ্য 28 সেমি.

∴ বহির্ব্যাসার্ধের দৈর্ঘ্য $=\frac{28}{2}=14$ সেমি.

প্রশ্নানুসারে,

$\pi \left ( 14 \right )^{2}-\pi r^{2}=269.5$

বা, $\frac{22}{7}\left ( 196-r^{2} \right )=269.5$

বা, $\left ( 196-r^{2} \right )=269.5\times \frac{7}{22}$

বা, $\left ( 196-r^{2} \right )=85.75$

বা, $-r^{2}=85.75 - 196$

বা, $-r^{2}=-110.25$

বা, $r^{2}=110.25$

∴ r = 10.5 সেমি.

অন্তর্ব্যাসের দৈর্ঘ্য

= 2r

= 2 × 10.5

= 21 সেমি.

উত্তরঃ অন্তর্ব্যাসের দৈর্ঘ্য 21 সেমি.

19. প্রতুল পাশের ছবির মতাে একটি সমবাহু ত্রিভুজ ABC এঁকেছে যার প্রতিটি বাহুর দৈর্ঘ্য 10 সেমি.। সুমিতা A, B ও C বিন্দুকে কেন্দ্র করে 5 সেমি. দৈর্ঘ্যের ব্যাসার্ধের তিনটি বৃত্তচাপ এঁকেছে এবং মাঝের কিছু জায়গা রঙিন করেছে। হিসাব করে রঙিন জায়গার ক্ষেত্রফল লিখি। [√3 = 1.732 (প্রায়)]।

বৃত্তের ক্ষেত্রফল

সমাধানঃ

যেহেতু ABC একটি সমবাহু ত্রিভুজ।
∴ ABC ত্রিভুজের প্রতিটি কোণের মান 60°

এখন, 60° কেন্দ্রীয় কোণ সম্পন্ন প্রতিটি বৃত্তকলার ক্ষেত্রফল,

$\small =\frac{\pi r^{2}}{360}\times \theta \; \; \; {\color{Blue} \left [ \theta =60 ^{\circ}; r=5 \; cm. \right ]}$

$\small =\frac{\pi \times 5^{2}}{360}\times 60$ cm²

$\small =\frac{25 \pi}{6}\; \; cm^{2}$

এখন, A, B, C বিন্দুগুলিকে কেন্দ্র করে 5 cm ব্যাসার্ধের যে তিনটি বৃত্তকলা অঙ্কন করা হয়েছে তার মোট ক্ষেত্রফল,

$\small =3\times \left ( \frac{25 \pi}{6} \right )\; \; cm^{2}$

$\small =\frac{25 \pi}{2}\; \; cm^{2}$

$\small =\frac{25}{2}\times \frac{22}{7}\; \; cm^{2}\; \; {\color{Blue} \left [ \pi\approx\frac{22}{7} \right ]}$

$\small =\frac{275}{7}\; \: cm^{2}$

$\small =39.29\; \: cm^{2}$ (প্রায়)

ABC সমবাহু ত্রিভুজের ক্ষেত্রফল,

$\small =\frac{\sqrt{3}}{4}$ × (সমান বাহুগুলির একটির দৈর্ঘ্য)²

$\small =\frac{1.732}{4}\times \left (10 \right )^{2}\; \; cm^{2}$ [√3 = 1.732 (প্রায়)]

$\small =\frac{1.732}{4}\times 100\; \; cm^{2}$ (প্রায়)

$\small =0.433\times 100\; \; cm^{2}$ (প্রায়)

$\small =43.3\; \; cm^{2}$ (প্রায়)

এখন, রঙিন অংশের ক্ষেত্রফল,

= (ABC সমবাহু ত্রিভুজের ক্ষেত্রফল) − (3টি বৃত্তকলার মোট ক্ষেত্রফল)

$\small =\left (43.3-39.29 \right )\; \; cm^{2}$ (প্রায়)

$\small =4.01\; \: cm^{2}$ (প্রায়)

উত্তরঃ নির্ণেয় রঙিন অংশের ক্ষেত্রফল 4.01 cm² প্রায়।

20. রাবেয়া একটি বড়াে কাগজে 21 সেমি. বাহুবিশিষ্ট সমবাহু ত্রিভুজ আঁকল। ওই সমবাহু ত্রিভুজের একটি অন্তর্বৃত্ত অঙ্কন করে বৃত্তাকার জায়গাটি রঙিন করল। আমি রঙিন জায়গার ক্ষেত্রফল হিসাব করে লিখি।

সমাধানঃ

সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য (a) = 21 সেমি.

∴ ত্রিভুজটির উচ্চতা (h)

$=\frac{\sqrt{3}}{2}a$

$=\frac{\sqrt{3}}{2}\times 21$

$=\frac{21\sqrt{3}}{2}$ সেমি.

ত্রিভুজটির অন্তর্বৃত্ত ব্যাসার্ধ (r)

$=\frac{1}{3}h$

$=\frac{1}{3}\times \frac{21\sqrt{3}}{2}$

$=\frac{7\sqrt{3}}{2}$

বৃত্তাকার জায়গার ক্ষেত্রফল

$=\pi r^{2}$

$=\frac{22}{7}\times \left (\frac{7\sqrt{3}}{2} \right )^{2}$

$=\frac{22}{7}\times \frac{49\times 3}{4}$

= 115.5 বর্গসেমি।

উত্তরঃ রঙিন জায়গার ক্ষেত্রফল 115.5 বর্গসেমি।

21. একটি সমবাহু ত্রিভুজের পরিবৃত্তের ক্ষেত্রফল 462 বর্গ সেমি। ত্রিভুজটির প্রতিটি বাহুর দৈর্ঘ্য হিসাব করে লিখি।

সমাধানঃ

ধরি, পরিবৃত্তের ব্যাসার্ধ r সেমি এবং সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য a সেমি ।

প্রশ্নানুসারে,

$\pi r^{2}=462$

বা, $\frac{22}{7}\times r^{2}=462$

বা, $r^{2}=462\times \frac{7}{22}$

বা, $r=\sqrt{21\times 7}$

$\therefore r=7\sqrt{3}$

সমবাহু ত্রিভুজের উচ্চতা

$=\frac{\sqrt{3}}{2}\times$ বাহু

$=\frac{\sqrt{3}}{2}\times a$

আবার, আমরা জানি,

সমবাহু ত্রিভুজের পরিবৃত্তের ব্যাসার্ধ

$r=\frac{2}{3}\times$ উচ্চতা

বা, $7\sqrt{3}=\frac{2}{3}\times \frac{\sqrt{3}}{2}\times a$

বা, $a=\frac{7\sqrt{3}\times 3\times 2}{2\sqrt{3}}$

∴ a = 21

উত্তরঃ সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য 21 সেমি ।

22. একটি ত্রিভুজের পরিসীমা 32 সেমি. এবং ত্রিভুজটির অন্তবৃত্তের ক্ষেত্রফল 38.5 বর্গ সেমি.। ত্রিভুজটির ক্ষেত্রফল হিসাব করে লিখি।

সমাধানঃ

ধরি, ত্রিভুজটির অন্তবৃত্তের ব্যাসার্ধ r সেমি.।

প্রশ্নানুসারে,

$\pi r^{2}=38.5$

বা, $\frac{22}{7}r^{2}=\frac{385}{10}$

বা, $r^{2}=\frac{385}{10}\times \frac{7}{22}$

বা, $r=\sqrt{\frac{7\times 7}{2\times 2}}$

বা, $r=\frac{7}{2}$

এখন,

Δ ABC এর ক্ষেত্রফল

= Δ AOB এর ক্ষেত্রফল + Δ BOC এর ক্ষেত্রফল + Δ AOC এর ক্ষেত্রফল

$=\frac{1}{2}\times AB\times OP+\frac{1}{2}\times BC\times OQ+\frac{1}{2}\times AC\times OR$

$=\frac{1}{2}\times AB\times r+\frac{1}{2}\times BC\times r+\frac{1}{2}\times AC\times r$

$=\frac{1}{2}\times r \times \left (AB+BC+AC \right )$

$=\frac{1}{2}\times \frac{7}{2}\times 32$

= 56 বর্গ সেমি.

উত্তরঃ ত্রিভুজটির ক্ষেত্রফল 56 বর্গ সেমি.।

23. 20 সেমি., 15 সেমি. এবং 25 সেমি. বাহুবিশিষ্ট ত্রিভুজের অন্তবৃত্ত ও পরিবৃত্তের ব্যাসার্ধের দৈর্ঘ্য হিসাব করে লিখি৷ অন্তবৃত্ত ও পরিবৃত্তের ক্ষেত্রফল হিসাব করে নির্ণয় করি।

সমাধানঃ

যেহেতু,

$20^{2}+15^{2}$

= 400 + 225

= 625

$=25^{2}$

∴ ত্রিভুজটি একটি সমকোণী ত্রিভুজ।

∴ ত্রিভুজটির ক্ষেত্রফল

$=\frac{1}{2}\times 20\times 15$

= 150 বর্গ সেমি

ধরি, অন্তর্বৃত্তের ব্যাসার্ধ OP = OQ = OR = r সেমি

এখন, Δ ABC এর ক্ষেত্রফল

= Δ AOB এর ক্ষেত্রফল + Δ BOC এর ক্ষেত্রফল + Δ AOC এর ক্ষেত্রফল

$=\frac{1}{2}\times AB\times OP+\frac{1}{2}\times BC\times OQ+\frac{1}{2}\times AC\times OR$

$=\frac{1}{2}\times AB\times r+\frac{1}{2}\times BC\times r+\frac{1}{2}\times AC\times r$

$=\frac{1}{2}\times r\left ( AB+BC+AC \right )$

$=\frac{r}{2}\times \left ( 15+20+25 \right )$

= 30r

প্রশ্নানুসারে,

30r = 150

বা, $r=\frac{150}{30}$

∴ r = 5

∴ ত্রিভুজটির অন্তর্বৃত্তের ব্যাসার্ধ 5 সেমি .

∴ ত্রিভুজটির অন্তর্বৃত্তের ক্ষেত্রফল

$=\pi \times \left ( 5 \right )^{2}$

$=\frac{22}{7}\times 25$

$=\frac{550}{7}$

$=78\frac{4}{7}$ বর্গ সেমি

আমরা জানি, সমকোণী ত্রিভুজের পরিবৃত্তের ব্যাসার্ধ অতিভুজের অর্ধেক হয়।

∴ ত্রিভুজটির পরিবৃত্তের ব্যাসার্ধ

$=\frac{25}{2}$ সেমি

∴ ত্রিভুজটির পরিবৃত্তের ক্ষেত্রফল

$=\pi \times \left ( \frac{25}{2} \right )^{2}$

$=\frac{22}{7}\times \frac{625}{4}$

$=\frac{6875}{14}$

$=491\frac{1}{14}$ বর্গ সেমি

উত্তরঃ ত্রিভুজটির অন্তর্বৃত্তের ব্যাসার্ধ 5 সেমি এবং পরিবৃত্তের ব্যাসার্ধ ${\color{DarkGreen} \frac{25}{2}}$ সেমি।

ত্রিভুজটির অন্তর্বৃত্তের ক্ষেত্রফল ${\color{DarkGreen} 78\frac{4}{7}}$ বর্গ সেমি এবং পরিবৃত্তের ক্ষেত্রফল ${\color{DarkGreen} 491\frac{1}{14}}$ বর্গ সেমি।

24. জয়া একটি বর্গক্ষেত্রের অন্তর্বৃত্ত অঙ্কন করল। ওই বৃত্তটি আবার একটি সমবাহু ত্রিভুজের পরিবৃত্ত যার প্রত্যেক বাহুর দৈর্ঘ্য ${\color{Blue} 4\sqrt{3}}$ সেমি.৷ বর্গক্ষেত্রটির একটি কর্ণের দৈর্ঘ্য হিসাব করে লিখি।

সমাধানঃ

প্রদত্ত,

সমবাহু ত্রিভুজের বাহুর দৈর্ঘ্য (a) = $4\sqrt{3}$ সেমি.৷

∴ সমবাহু ত্রিভুজের উচ্চতা (h)

$=\frac{\sqrt{3}}{2}\times 4\sqrt{3}$

= 6 সেমি.

∴ সমবাহু ত্রিভুজের পরিবৃত্তের ব্যাসার্ধ

$=\frac{2}{3}\times h$

$=\frac{2}{3}\times 6$

= 4 সেমি.

∴ বৃত্তটির ব্যাস

= 2 × 4

= 8 সেমি.

এখন বৃত্তটির ব্যাস = বর্গক্ষেত্রের বাহুর দৈর্ঘ্য = 8 সেমি.

∴ বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য

= বর্গক্ষেত্রের বাহুর দৈর্ঘ্য × $\sqrt{2}$

$=8\times \sqrt{2}$

$=8\sqrt{2}$ সেমি.

উত্তরঃ বর্গক্ষেত্রটির একটি কর্ণের দৈর্ঘ্য ${\color{DarkGreen} 8\sqrt{2}}$ সেমি.

25. সুমিত একটি তারকে দুটি সমান অংশে কাটল। একটি অংশকে বর্গাকারে ও অপর অংশটিকে বৃত্তাকারে বাঁকাল। বৃত্তাকার তারটি বর্গাকার তারটির থেকে 33 বর্গসেমি. বেশি জায়গা নিলে তারটির প্রকৃত দৈর্ঘ্য হিসাব করে লিখি।

সমাধানঃ

ধরি, বৃত্তাকার তারটির ব্যাসার্ধ r সেমি এবং বর্গাকার তারটির বাহুর দৈর্ঘ্য a সেমি।

∴ বৃত্তাকার তারটির ক্ষেত্রফল $=\pi r^{2}$ বর্গসেমি।

∴ বর্গাকার তারটির ক্ষেত্রফল $\left ( a^{2} \right )=\pi r^{2}-33$ বর্গসেমি।

∴ বর্গাকার তারটির বাহুর দৈর্ঘ্য $\left ( a \right )=\sqrt{\pi r^{2}-33}$ সেমি।

∴ বর্গাকার তারটির পরিসীমা $\left ( 4a \right )=4\times \sqrt{\pi r^{2}-33}$ সেমি।

∴ বৃত্তাকার তারটির পরিধি $=2\pi r$ সেমি।

প্রশ্নানুসারে,

$4\times \sqrt{\pi r^{2}-33}=2\pi r$

বা, $\left (4\times \sqrt{\pi r^{2}-33} \right )^{2}=\left (2\pi r \right )^{2}$

বা, $16\left (\pi r^{2}-33 \right )=4\pi^{2} r^{2}$

বা, $16\pi r^{2}-16\times 33 -4\pi^{2} r^{2}=0$

বা, $4\pi r^{2}\left ( 4-\pi \right )=16\times 33$

বা, $4\times \frac{22}{7}\times r^{2}\times \left ( 4-\frac{22}{7} \right )=16\times 33$

বা, $r^{2}\times \left ( \frac{28-22}{7} \right )=16\times 33\times \frac{7}{22\times 4}$

বা, $r^{2}=16\times 33\times \frac{7}{22\times 4}\times \frac{7}{6}$

বা, $r^{2}=7\times 7$

∴ r = 7

∴ বৃত্তাকার তারটির পরিধি

$=2\pi r$

$=2\times \frac{22}{7}\times 7$

= 44 সেমি।

= বর্গক্ষেত্রের পরিসীমা

∴ তারটির দৈর্ঘ্য = 44 + 44 = 88 সেমি।

উত্তরঃ তারটির প্রকৃত দৈর্ঘ্য 88 সেমি।

26. বহু পছন্দভিত্তিক প্রশ্ন (M.C.Q.) :

(i) একটি বৃত্তকার ক্ষেত্রের ক্ষেত্রফল x বর্গএকক, পরিধি y একক ও ব্যাসের দৈর্ঘ্য z একক হলে $\dpi{100} \small {\color{Blue} \frac{x}{yz}}$ -এর মান

(a) $\dpi{100} \small {\color{Blue} \frac{1}{2}}$

(b) $\dpi{100} \small {\color{Blue} \frac{1}{4}}$

(d) $\dpi{100} \small {\color{Blue} \frac{1}{8}}$

সমাধানঃ

ধরি, বৃত্তাকার ক্ষেত্রের ব্যাসার্ধ r একক।

∴ বৃত্তকার ক্ষেত্রের ব্যাসের দৈর্ঘ্য z = 2r একক,

ক্ষেত্রফল $\left ( x \right )=\pi r^{2}$ বর্গএকক,

এবং

পরিধি $\left ( y \right )=2\pi r$ একক

∴ $\dpi{100} \small \frac{x}{yz}$ -এর মান

$=\frac{\pi r^{2}}{2\pi r\times 2r}$

$=\frac{1}{4}$

উত্তরঃ (b) $\dpi{100} \small {\color{DarkGreen} \frac{1}{4}}$

26. বহু পছন্দভিত্তিক প্রশ্ন (M.C.Q.) :

(ii) একটি বৃত্তের পরিলিখিত ও অন্তলিখিত বর্গক্ষেত্রদ্বয়ের ক্ষেত্রফলের অনুপাত

(a) 4 : 1

(b) 1 : 4

(d) 1 : 2

সমাধানঃ

ধরি, বৃত্তাকার ক্ষেত্রের ব্যাসার্ধ r একক।

বৃত্তের পরিলিখিত বর্গক্ষেত্রের বাহু (a) = বৃত্তের ব্যাস = 2r একক।

∴ বৃত্তের পরিলিখিত বর্গক্ষেত্রের ক্ষেত্রফল $=\left ( 2r \right )^{2}=4r^{2}$ বর্গ একক

আবার, বৃত্তের অন্তর্লিখিত বর্গক্ষেত্রের কর্ণ $\left ( a\sqrt{2} \right )$ = বৃত্তের ব্যাস = 2r একক।

$\therefore a\sqrt{2}=2r$

বা, $a=\frac{2r}{\sqrt{2}}$

$\therefore a=\sqrt{2}r$

∴ বৃত্তের অন্তর্লিখিত বর্গক্ষেত্রের ক্ষেত্রফল $=\left ( \sqrt{2}r \right )^{2}=2r^{2}$ বর্গ একক

∴ বৃত্তের পরিলিখিত ও অন্তর্লিখিত বর্গক্ষেত্রের ক্ষেত্রফলের অনুপাত

$=4r^{2}:2r^{2}$

= 2 : 1

উত্তরঃ (c) 2 : 1

26. বহু পছন্দভিত্তিক প্রশ্ন (M.C.Q.) :

(iii) একটি বৃত্তকার ক্ষেত্রের পরিধি ও ক্ষেত্রফলের সাংখ্যমান সমান। ওই বৃত্তের পরিলিখিত বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য

(a) 4 একক

(b) 2 একক

(d) $\dpi{100} \small {\color{Blue} 2\sqrt{2}}$ একক

সমাধানঃ

ধরি, বৃত্তাকার ক্ষেত্রের ব্যাসার্ধ r একক।

প্রশ্নানুসারে,

$2\pi r=\pi r^{2}$

বা, 2 = r

∴ r = 2

∴ বৃত্তের পরিলিখিত বর্গক্ষেত্রের বাহু = বৃত্তের ব্যাস = 2r = 2 × 2 = 4 একক

∴ বৃত্তের পরিলিখিত বর্গক্ষেত্রের কর্ণের দৈর্ঘ্য = বাহু × $\sqrt{2}=4\sqrt{2}$ একক।

উত্তরঃ (c) $\dpi{100} {\color{DarkGreen} 4\sqrt{2}}$ একক

26. বহু পছন্দভিত্তিক প্রশ্ন (M.C.Q.) :

(iv) একটি সমবাহু ত্রিভুজের পরিলিখিত ও অন্তলিখিত বৃত্তাকার ক্ষেত্রের ক্ষেত্রফলের অনুপাত

(a) 4 : 1

(b) 1 : 4

(d) 1 : 2

সমাধানঃ

আমরা জানি,

সমবাহু ত্রিভুজের পরিলিখিত ও অন্তলিখিত বৃত্তাকার ক্ষেত্রের ব্যাসার্ধের অনুপাত 2 : 1

∴ সমবাহু ত্রিভুজের পরিলিখিত ও অন্তলিখিত বৃত্তাকার ক্ষেত্রের ক্ষেত্রফলের অনুপাত

$=\pi \times \left ( 2 \right )^{2}:=\pi \times \left ( 1 \right )^{2}$

= 4 : 1

উত্তরঃ (a) 4 : 1

26. বহু পছন্দভিত্তিক প্রশ্ন (M.C.Q.) :

(v) একটি বলয়াকৃতি লােহার পাতের অন্তর্ব্যাস 20 সেমি. এবং বহির্ব্যাস 22 সেমি.। বলয়টিতে লােহার পাত আছে(a) 22 বর্গসেমি.

(b) 44 বর্গসেমি.

(d) 88 বর্গসেমি.

সমাধানঃ

বলয়াকৃতি লােহার পাতের অন্তর্ব্যাস 20 সেমি. এবং বহির্ব্যাস 22 সেমি.

∴ অন্তর্ব্যাসার্ধ 10 সেমি. এবং বহির্ব্যাসার্ধ 11 সেমি.

এখন, বলয়টিতে লোহার পাত আছে

$=\pi \times \left ( 11 \right )^{2}-\pi \times \left ( 10 \right )^{2}$

$=\pi \times \left ( 121-100 \right )$

$=\frac{22}{7}\times 21$

= 66 বর্গসেমি.

উত্তরঃ (c) 66 বর্গসেমি.

27. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন :

(i) একটি বৃত্তাকার ক্ষেত্রের ব্যাসার্ধের দৈর্ঘ্য 10% বৃদ্ধি করলে বৃত্তাকার ক্ষেত্রের ক্ষেত্রফল শতকরা কত বৃদ্ধি পায় হিসাব করি।

সমাধানঃ

ধরি, বৃত্তাকার ক্ষেত্রের ব্যাসার্ধ ছিল r একক।

∴ ক্ষেত্রফল ছিল $\pi r^{2}$ বর্গ একক।

ব্যাসার্ধের দৈর্ঘ্য 10% বৃদ্ধি করলে বৃত্তাকার ক্ষেত্রের নতুন ব্যাসার্ধ

$=r+r\times \frac{10}{100}$

$=r+\frac{r}{10}$

$=\frac{11r}{10}$ একক

∴ এখন বৃত্তাকার ক্ষেত্রটির নতুন ক্ষেত্রফল হবে

$=\pi \times \left ( \frac{11r}{10} \right )^{2}$

$=\frac{121}{100}\pi r^{2}$ বর্গ একক

ক্ষেত্রফল বৃদ্ধি পেয়েছে

$=\frac{121}{100}\pi r^{2}-\pi r^{2}$

$=\frac{121\pi r^{2}-100\pi r^{2}}{100}$

$=\frac{21}{100}\pi r^{2}$ বর্গ একক

∴ বৃত্তাকার ক্ষেত্রের ক্ষেত্রফল শতকরা বৃদ্ধি পায়

$=\frac{\frac{21\pi r^{2}}{100}}{\pi r^{2}}\times 100$

$=\frac{21\pi r^{2}}{100}\times \frac{1}{\pi r^{2}}\times 100$

= 21 %

উত্তরঃ বৃত্তাকার ক্ষেত্রের ক্ষেত্রফল শতকরা 21% বৃদ্ধি পায়।

27. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন :

(ii) একটি বৃত্তাকার ক্ষেত্রের পরিসীমা 50% হ্রাস করলে বৃত্তাকার ক্ষেত্রের ক্ষেত্রফল শতকরা কত হ্রাস পায় হিসাব করি।

সমাধানঃ

ধরি, বৃত্তাকার ক্ষেত্রের ব্যাসার্ধ ছিল r একক।

∴ পরিসীমা ছিল $=2\pi r$ একক এবং ক্ষেত্রফল ছিল $\pi r^{2}$ বর্গ একক।

পরিসীমা 50% হ্রাস করলে বৃত্তাকার ক্ষেত্রের নতুন পরিসীমা হবে

$=2\pi r-2\pi r\times \frac{50}{100}$

$=2\pi r-\pi r$

$=\pi r$ একক

$=2\times \pi \times \frac{r}{2}$ একক

∴ এখন বৃত্তাকার ক্ষেত্রটির নতুন ব্যাসার্ধ হবে $=\frac{r}{2}$ একক

∴ এখন বৃত্তাকার ক্ষেত্রটির নতুন ক্ষেত্রফল হবে

$=\pi \times \left ( \frac{r}{2} \right )^{2}$

$=\frac{\pi r^{2}}{4}$ বর্গ একক

ক্ষেত্রফল হ্রাস পেয়েছে

$=\pi r^{2}-\frac{\pi r^{2}}{4}$

$=\frac{4\pi r^{2}-\pi r^{2}}{4}$

$=\frac{3}{4}\pi r^{2}$ বর্গ একক

∴ বৃত্তাকার ক্ষেত্রের ক্ষেত্রফল শতকরা হ্রাস পায়

$=\frac{\frac{3\pi r^{2}}{4}}{\pi r^{2}}\times 100$

$=\frac{3\pi r^{2}}{4}\times \frac{1}{\pi r^{2}}\times 100$

= 75 %

উত্তরঃ বৃত্তাকার ক্ষেত্রের ক্ষেত্রফল শতকরা 75 % হ্রাস পায়।

27. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন :

(iii) একটি বৃত্তাকার ক্ষেত্রের ব্যাসার্ধের দৈর্ঘ্য r মিটার। অন্য একটি বৃত্তাকার ক্ষেত্রের ব্যাসার্ধের দৈর্ঘ্য কত হলে তার ক্ষেত্রফল প্রথম বৃত্তের ক্ষেত্রফলের x গুণ হবে তা হিসাব করে দেখি।

সমাধানঃ

প্রথম বৃত্তের ব্যাসার্ধের দৈর্ঘ্য r মিটার।

∴ প্রথম বৃত্তের ক্ষেত্রফল $=\pi r^{2}$ বর্গ মিটার।

প্রশ্নানুসারে,

দ্বিতীয় বৃত্তের ক্ষেত্রফল

= x × প্রথম বৃত্তের ক্ষেত্রফল

$=x\pi r^{2}$ বর্গমিটার

$=\pi \times \left ( \sqrt{x}r \right )^{2}$ বর্গমিটার।

উত্তরঃ দ্বিতীয় বৃত্তের ব্যাসার্ধের দৈর্ঘ্য ${\color{DarkGreen} \sqrt{x}r}$ মিটার।

27. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন :

(iv) 3 সেমি., 4 সেমি. ও 5 সেমি. বাহুবিশিষ্ট ত্রিভুজের পরিবৃত্তের ক্ষেত্রফল কত হিসাব করি।

সমাধানঃ

$3^{2}+4^{2}=5^{2}$ ∴ ত্রিভুজটি একটি সমকোণী ত্রিভুজ।

আমরা জানি, সমকোণী ত্রিভুজের পরিবৃত্তের কেন্দ্র ত্রিভুজটির অতিভুজের মধ্যবিন্দুতে অবস্থিত হয়।

∴ ত্রিভুজটির পরিবৃত্তের ব্যাসার্ধ $=\frac{5}{2}$ সেমি

∴ ত্রিভুজটির পরিবৃত্তের ক্ষেত্রফল

$=\pi \times \left ( \frac{5}{2} \right )^{2}$

$=\frac{22}{7}\times \frac{25}{4}$

$=\frac{275}{14}$

$=19\frac{9}{14}$

উত্তরঃ ত্রিভুজটির পরিবৃত্তের ক্ষেত্রফল ${\color{DarkGreen} 19\frac{9}{14}}$ বর্গ সেমি।

27. সংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন :

(v) সমবেধবিশিষ্ট একটি টিনের পাত থেকে তিনটি বৃত্তাকার চাকতি কেটে নেওয়া হলাে। বৃত্তাকার চাকতি তিনটির ব্যাসের দৈর্ঘ্যের অনুপাত 3 : 5 : 7 হলে তাদের ওজনের অনুপাত কত হিসাব করে দেখি।

সমাধানঃ

যেহেতু, বৃত্তাকার চাকতি তিনটির ব্যাসের দৈর্ঘ্যের অনুপাত 3 : 5 : 7

∴ বৃত্তাকার চাকতি তিনটির ব্যাসার্ধের দৈর্ঘ্যের অনুপাত 3 : 5 : 7

ধরি, বৃত্তাকার চাকতি তিনটির ব্যাসার্ধের দৈর্ঘ্য যথাক্রমে 3r, 5r এবং 7r

∴ বৃত্তাকার চাকতি তিনটির ক্ষেত্রফলের অনুপাত

$=\pi \times \left ( 3r \right )^{2}:\pi \times \left ( 5r \right )^{2}:\pi \times \left ( 7r \right )^{2}$

$=9r^{2}:25r^{2}:49r^{2}$

= 9 : 25 : 49

উত্তরঃ বৃত্তাকার চাকতি তিনটির ওজনের অনুপাত 9 : 25 : 49