Koshe Dekhi 23.2 Class 10

koshe dekhi 23.2 class 10

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q1. আমাদের বাড়ির জানালায় একটি মই ভূমির সঙ্গে 60° কোণে রাখা আছে। মইটি $2\sqrt{3}$ মিটার লম্বা হলে আমাদের এই জানালাটি ভূমি থেকে কত উপরে আছে ছবি এঁকে হিসাব করে লিখি।

সমাধান :

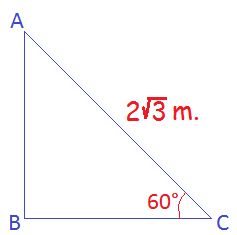
ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

AB = ?

আমরা জানি,

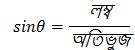
$sin \theta$

বা, $sin\theta =\frac{AB}{AC}$

বা, $sin60^{\circ}=\frac{AB}{2\sqrt{3}}$

বা, $\frac{\sqrt{3}}{2}=\frac{AB}{2\sqrt{3}}$ ${\color{Blue} \left [ \because sin60^{\circ}=\frac{\sqrt{3}}{2} \right ]}$

বা, $AB=\sqrt{3}\times \sqrt{3}$

∴ AB = 3

উত্তরঃ নির্ণেয় জানালাটি ভূমি থেকে 3 মিটার উপরে আছে।

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q2. ABC সমকোণী ত্রিভুজের $\angle B$ সমকোণ। $AB=8\sqrt{3}$ সেমি এবং BC = 8 সেমি হলে $\angle ACB$ ও $\angle BAC$ এর মান হিসাব করে লিখি।

সমাধান :

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

আমরা জানি,

$tan \theta$

$tan\angle ACB=\frac{AB}{BC}$

বা, $tan\angle ACB=\frac{8\sqrt{3}}{8}$

বা, $tan\angle ACB=\sqrt{3}$

বা, $tan\angle ACB=tan60^{\circ}$ ${\color{Blue} \left [ \because tan60^{\circ}=\sqrt{3} \right ]}$

$\therefore \angle ACB=60^{\circ}$

এবং

$tan\angle BAC=\frac{BC}{AB}$

বা, $tan\angle BAC=\frac{8}{8\sqrt{3}}$

বা, $tan\angle BAC=\frac{1}{\sqrt{3}}$

বা, $tan\angle BAC=tan30^{\circ}$ ${\color{Blue} \left [ \because tan30^{\circ}=\frac{1}{\sqrt{3}} \right ]}$

$\therefore \angle BAC=30^{\circ}$

উত্তরঃ নির্ণেয়, ${\color{DarkGreen} \angle ACB=60^{\circ};\angle BAC=30^{\circ}}$

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q3. ABC সমকোণী ত্রিভুজের $\angle B=90^{\circ},\angle A=30^{\circ}$ এবং AC = 20 সেমি.। BC ও AB বাহুদ্বয়ের দৈর্ঘ্য হিসাব করে লিখি।

সমাধান :

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

আমরা জানি,

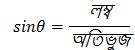
$sin \theta$

$sin\angle BAC=\frac{BC}{AC}$

$\Rightarrow sin30{^{\circ}}=\frac{BC}{20}$

$\Rightarrow \frac{1}{2}=\frac{BC}{20}$ ${\color{Blue} [\because sin30^{\circ}=\frac{1}{2}]}$

$\Rightarrow 2BC=20$

$\Rightarrow BC=\frac{20}{2}$

$\therefore BC=10$ সেমি.

আবার,

আমরা জানি,

$cos \theta$

$cos\angle BAC =\frac{AB}{AC}$

$\Rightarrow cos30^{\circ}=\frac{AB}{20}$

$\Rightarrow \frac{\sqrt{3}}{2}=\frac{AB}{20}\; \; {\color{Blue} [\because cos30^{\circ}=\frac{\sqrt{3}}{2}]}$

$\Rightarrow 2AB=20\sqrt{3} \\$

$\Rightarrow AB=\frac{20\sqrt{3}}{2}$

$\therefore AB=10\sqrt{3}$ সেমি.

উত্তরঃ নির্ণেয়, AB = ${\color{DarkGreen} 10\sqrt{3}}$ সেমি. এবং BC = 10 সেমি.।

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q4. PQR সমকোণী ত্রিভুজের $\angle Q=90^{\circ},\angle R=45^{\circ};$ যদি PR = $3\sqrt{2}$ মিটার হয়, তাহলে PQ ও QR বাহুদ্বয়ের দৈঘ্য নির্ণয় করি।

সমাধান :

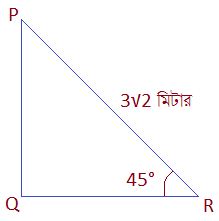
ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

আমরা জানি,

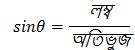
$sin \theta$

$sin\angle QRP=\frac{PQ}{PR}$

$\Rightarrow sin45{^{\circ}}=\frac{PQ}{3\sqrt{2}}$

$\Rightarrow \frac{1}{\sqrt{2}}=\frac{PQ}{3\sqrt{2}}$ ${\color{Blue} [\because sin45^{\circ}=\frac{1}{\sqrt {2}}]}$

$\Rightarrow \sqrt {2}PQ=3 \sqrt {2}$

$\Rightarrow PQ=\frac{3\sqrt{2}}{\sqrt{2}}$

$\therefore PQ=3$ সেমি.

আবার, যেহেতু, $\Delta PQR$ একটি সমদ্বিবাহু ত্রিভুজ, যার PQ = QR. [ $\because$ $\angle R=\angle P=45^{\circ}$ ]

∴ PQ = QR = 3 সেমি.।

উত্তরঃ নির্ণেয়, PQ = QR = 3 সেমি.।

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q5. মান নির্ণয় করি : (i) ${{\sin }^{2}}45{}^\circ -\text{cose}{{\text{c}}^{2}}60{}^\circ +{{\sec }^{2}}30{}^\circ$

সমাধান :

প্রদত্ত,

${{\sin }^{2}}45{}^\circ -\text{cose}{{\text{c}}^{2}}60{}^\circ +{{\sec }^{2}}30{}^\circ$

$=\left ( \frac{1}{\sqrt{2}} \right )^{2}-\left ( \frac{2}{\sqrt{3}} \right )^{2}+\left ( \frac{2}{\sqrt{3}} \right )^{2}$ ${\color{Blue} \left [ \because sin45^{\circ}=\frac{1}{\sqrt{2}}, cosec60^{\circ}=\frac{2}{\sqrt{3}}, sec30^{\circ}=\frac{2}{\sqrt{3}} \right ]}$

$=\left ( \frac{1}{\sqrt{2}} \right )^{2}$

$=\frac{1}{\sqrt{2}}\times \frac{1}{\sqrt{2}}$

$=\frac{1}{2}$

উত্তরঃ নির্ণেয় ${\color{DarkGreen} {{\sin }^{2}}45{}^\circ -\text{cose}{{\text{c}}^{2}}60{}^\circ +{{\sec }^{2}}30{}^\circ}$ এর মান ${\color{DarkGreen} \frac{1}{2}}$

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q5. মান নির্ণয় করি : (ii) ${{\sec }^{2}}45{}^\circ -{{\cot }^{2}}45{}^\circ -{{\sin }^{2}}30{}^\circ -{{\sin }^{2}}60{}^\circ$

সমাধান :

প্রদত্ত

${{\sec }^{2}}45{}^\circ -{{\cot }^{2}}45{}^\circ -{{\sin }^{2}}30{}^\circ -{{\sin }^{2}}60{}^\circ$

$=\left ( \sqrt{2} \right )^{2}-\left ( 1 \right )^{2}-\left ( \frac{1}{2} \right )^{2}-\left ( \frac{\sqrt{3}}{2} \right )^{2}$

$=2-1-\frac{1}{4}-\frac{3}{4}$

$=\frac{8-4-1-3}{4}$

$=\frac{8-8}{4}$

$=\frac{0}{4}$

= 0

উত্তরঃ নির্ণেয় ${\color{DarkGreen} {{\sec }^{2}}45{}^\circ -{{\cot }^{2}}45{}^\circ -{{\sin }^{2}}30{}^\circ -{{\sin }^{2}}60{}^\circ}$ এর মান 0

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q5. মান নির্ণয় করি : (iii) $3{{\tan }^{2}}45{}^\circ -{{\sin }^{2}}60{}^\circ -\frac{1}{3}{{\cot }^{2}}30{}^\circ -\frac{1}{8}{{\sec }^{2}}45{}^\circ$

সমাধান :

প্রদত্ত

$3{{\tan }^{2}}45{}^\circ -{{\sin }^{2}}60{}^\circ -\frac{1}{3}{{\cot }^{2}}30{}^\circ -\frac{1}{8}{{\sec }^{2}}45{}^\circ$

$=3\times \left ( 1 \right )^{2}-\left ( \frac{\sqrt{3}}{2} \right )^{2}-\frac{1}{3}\times \left ( \sqrt{3} \right )^{2}-\frac{1}{8}\times \left ( \sqrt{2} \right )^{2}$

$=3-\frac{3}{4}-\frac{1}{3}\times 3-\frac{1}{8}\times 2$

$=3-\frac{3}{4}-1-\frac{1}{4}$

$=\frac{12-3-4-1}{4}$

$=\frac{12-8}{4}$

$=\frac{4}{4}$

= 1

উত্তরঃ নির্ণেয় ${\color{DarkGreen} 3{{\tan }^{2}}45{}^\circ -{{\sin }^{2}}60{}^\circ -\frac{1}{3}{{\cot }^{2}}30{}^\circ -\frac{1}{8}{{\sec }^{2}}45{}^\circ}$ এর মান 1

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q5. মান নির্ণয় করি : (iv) $\frac{4}{3}{{\cot }^{2}}30{}^\circ +3{{\sin }^{2}}60{}^\circ -2\text{cose}{{\text{c}}^{2}}60{}^\circ -\frac{3}{4}{{\tan }^{2}}30{}^\circ$

সমাধান :

প্রদত্ত

$\frac{4}{3}{{\cot }^{2}}30{}^\circ +3{{\sin }^{2}}60{}^\circ -2\text{cose}{{\text{c}}^{2}}60{}^\circ -\frac{3}{4}{{\tan }^{2}}30{}^\circ$

$=\frac{4}{3}\times \left ( \sqrt{3} \right )^{2}+3\times \left ( \frac{\sqrt{3}}{2} \right )^{2}-2\times \left ( \frac{2}{\sqrt{3}} \right )^{2}-\frac{3}{4}\times \left ( \frac{1}{\sqrt{3}} \right )^{2}$

$=\frac{4}{3}\times 3+3\times \frac{3}{4}-2\times \frac{4}{3}-\frac{3}{4}\times \frac{1}{3}$

$=4+\frac{9}{4}-\frac{8}{3}-\frac{1}{4}$

$=\frac{48+27-32-3}{12}$

$=\frac{75-35}{12}$

$=\frac{40}{12}$

$=\frac{10}{3}$

$=3\frac{1}{3}$

উত্তরঃ নির্ণেয় ${\color{DarkGreen} \frac{4}{3}{{\cot }^{2}}30{}^\circ +3{{\sin }^{2}}60{}^\circ -2\text{cose}{{\text{c}}^{2}}60{}^\circ -\frac{3}{4}{{\tan }^{2}}30{}^\circ}$ এর মান ${\color{DarkGreen} 3\frac{1}{3}}$

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q5. মান নির্ণয় করি : (v) $\frac{\frac{1}{3}\cos 30{}^\circ }{\frac{1}{2}\sin 45{}^\circ }+\frac{\tan 60{}^\circ }{\cos 30{}^\circ }$

সমাধান :

প্রদত্ত

$\frac{\frac{1}{3}\cos 30{}^\circ }{\frac{1}{2}\sin 45{}^\circ }+\frac{\tan 60{}^\circ }{\cos 30{}^\circ }$

$=\frac{\frac{1}{3}\times \frac{\sqrt{3}}{2}}{\frac{1}{2}\times \frac{1}{\sqrt{2}}}+\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$ ${\color{Blue} \left [ \because cos30^{\circ}=\frac{\sqrt{3}}{2}, sin45^{\circ}=\frac{1}{\sqrt{2}}, tan60^{\circ}=\sqrt{3}, cos30^{\circ}=\frac{\sqrt{3}}{2} \right ]}$

$=\frac{\frac{1}{2\sqrt{3}}}{\frac{1}{2\sqrt{2}}}+\frac{\sqrt{3}}{\frac{\sqrt{3}}{2}}$

$=\left ( \frac{1}{2\sqrt{3}}\times \frac{2\sqrt{2}}{1} \right )+\left ( \sqrt{3}\times \frac{2}{\sqrt{3}} \right )$

$=\frac{\sqrt{2}}{\sqrt{3}}+2$

$=\frac{\sqrt{2}+2\sqrt{3}}{\sqrt{3}}$

$=\frac{\sqrt{3}\left (\sqrt{2}+2\sqrt{3} \right )}{\sqrt{3}\times \sqrt{3}}$ { লব ও হর উভয়কে ${\color{Blue} \sqrt{3}}$ দিয়ে গুন্ করে পাই ]

$=\frac{\sqrt{6}+6}{3}$

উত্তরঃ নির্ণেয় ${\color{DarkGreen} \frac{\frac{1}{3}\cos 30{}^\circ }{\frac{1}{2}\sin 45{}^\circ }+\frac{\tan 60{}^\circ }{\cos 30{}^\circ }}$ এর মান ${\color{DarkGreen} \frac{\sqrt{6}+6}{3}}$

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q5. মান নির্ণয় করি : (vi) ${{\cot }^{2}}30{}^\circ -2{{\cos }^{2}}60{}^\circ -\frac{3}{4}{{\sec }^{2}}45{}^\circ -4{{\sin }^{2}}30{}^\circ$

সমাধান :

প্রদত্ত,

${{\cot }^{2}}30{}^\circ -2{{\cos }^{2}}60{}^\circ -\frac{3}{4}{{\sec }^{2}}45{}^\circ -4{{\sin }^{2}}30{}^\circ$

$=\left ( \sqrt{3} \right )^{2}-2\times \left ( \frac{1}{2} \right )^{2}-\frac{3}{4}\times \left ( \sqrt{2} \right )^{2}-4\times \left ( \frac{1}{2} \right )^{2}$

$=3-2\times \frac{1}{4}-\frac{3}{4}\times 2-4\times \frac{1}{4}$

$=3-\frac{1}{2}-\frac{3}{2}-1$

$=\frac{6-1-3-2}{2}$

$=\frac{6-6}{2}$

$=\frac{0}{2}=0$

উত্তরঃ নির্ণেয় ${\color{DarkGreen} {{\cot }^{2}}30{}^\circ -2{{\cos }^{2}}60{}^\circ -\frac{3}{4}{{\sec }^{2}}45{}^\circ -4{{\sin }^{2}}30{}^\circ}$ এর মান 0 .

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q5. মান নির্ণয় করি : (vii) ${{\sec }^{2}}60{}^\circ -{{\cot }^{2}}30{}^\circ -\frac{2\tan 30{}^\circ \text{cosec}60{}^\circ }{1+{{\tan }^{2}}30{}^\circ }$

সমাধান :

প্রদত্ত

${{\sec }^{2}}60{}^\circ -{{\cot }^{2}}30{}^\circ -\frac{2\tan 30{}^\circ \text{cosec}60{}^\circ }{1+{{\tan }^{2}}30{}^\circ }$

$=\left ( \sqrt{3} \right )^{2}-2\times \left ( \frac{1}{2} \right )^{2}-\frac{3}{4}\times \left ( \sqrt{2} \right )^{2}-4\times \left ( \frac{1}{2} \right )^{2}$

$=3-\frac{1}{2}-\frac{3}{2}-1$

$=\frac{6-1-3-2}{2}$

$=\frac{6-6}{2}$

$=\frac{0}{2}=0$

উত্তরঃ নির্ণেয় ${\color{DarkGreen} {{\sec }^{2}}60{}^\circ -{{\cot }^{2}}30{}^\circ -\frac{2\tan 30{}^\circ \text{cosec}60{}^\circ }{1+{{\tan }^{2}}30{}^\circ }}$ এর মান 0 .

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q5. মান নির্ণয় করি : (viii) $\frac{\tan 60{}^\circ -\tan 30{}^\circ }{1+\tan 60{}^\circ \tan 30{}^\circ }+\cos 60{}^\circ \cos 30{}^\circ +\sin 60{}^\circ \sin 30{}^\circ$

সমাধান :

প্রদত্ত

$\frac{\tan 60{}^\circ -\tan 30{}^\circ }{1+\tan 60{}^\circ \tan 30{}^\circ }+\cos 60{}^\circ \cos 30{}^\circ +\sin 60{}^\circ \sin 30{}^\circ$

$=\frac{\sqrt{3}-\frac{1}{\sqrt{3}}}{1+\sqrt{3}\times \frac{1}{\sqrt{3}}}+\frac{1}{2}\times \frac{\sqrt{3}}{2}+\frac{\sqrt{3}}{2}\times \frac{1}{2}$

$=\frac{\frac{\sqrt{3}-1}{\sqrt{3}}}{1+1}+\frac{\sqrt{3}}{4}+\frac{\sqrt{3}}{4}$

$=\frac{\sqrt{3}-1}{2\sqrt{3}}+\frac{2\sqrt{3}}{4}$

$=\frac{\sqrt{3}\left (\sqrt{3}-1 \right )}{\sqrt{3}\times 2\sqrt{3}}+\frac{2\sqrt{3}}{4}$

$=\frac{3-\sqrt{3}}{6}+\frac{2\sqrt{3}}{4}$

$=\frac{2\left ( 3-\sqrt{3} \right )+3\times 2\sqrt{3}}{12}$

$=\frac{6-2\sqrt{3}+6\sqrt{3}}{12}$

$=\frac{6+4\sqrt{3}}{12}$

$=\frac{2\left ( 3+2\sqrt{3} \right )}{2\times 6}$

$=\frac{\left ( 3+2\sqrt{3} \right )}{6}$

উত্তরঃ নির্ণেয় ${\color{DarkGreen} \frac{\tan 60{}^\circ -\tan 30{}^\circ }{1+\tan 60{}^\circ \tan 30{}^\circ }+\cos 60{}^\circ \cos 30{}^\circ +\sin 60{}^\circ \sin 30{}^\circ}$ এর মান ${\color{DarkGreen} \frac{\left ( 3+2\sqrt{3} \right )}{6}}$

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q5. মান নির্ণয় করি : (ix) $\frac{1-{{\sin }^{2}}30{}^\circ }{1+{{\sin }^{2}}45{}^\circ }\times \frac{{{\cos }^{2}}60{}^\circ +{{\cos }^{2}}30{}^\circ }{\text{cose}{{\text{c}}^{2}}90{}^\circ -{{\cot }^{2}}90{}^\circ }\div \left( \sin 60{}^\circ \tan 30{}^\circ \right)$

সমাধান :

প্রদত্ত

$\frac{1-{{\sin }^{2}}30{}^\circ }{1+{{\sin }^{2}}45{}^\circ }\times \frac{{{\cos }^{2}}60{}^\circ +{{\cos }^{2}}30{}^\circ }{\text{cose}{{\text{c}}^{2}}90{}^\circ -{{\cot }^{2}}90{}^\circ }\div \left( \sin 60{}^\circ \tan 30{}^\circ \right)$

$=\frac{1-\left ( \frac{1}{2} \right )^{2}}{1+\left ( \frac{1}{\sqrt{2}} \right )^{2}}\times \frac{\left ( \frac{1}{2} \right )^{2}+\left ( \frac{\sqrt{3}}{2} \right )^{2}}{\left ( 1 \right )^{2}-\left ( 0 \right )^{2}}$ $\div \left( \frac{\sqrt{3}}{2}\times \frac{1}{\sqrt{3}} \right)$

$=\frac{1-\frac{1}{4}}{1+\frac{1}{2}}\times \frac{\frac{1}{4}+\frac{3}{4}}{1}$ $\div \frac{1}{2}$

$=\frac{\frac{3}{4}}{\frac{3}{2}}\times \frac{\frac{4}{4}}{1}$ $\div \frac{1}{2}$

$=\frac{3}{4}\times \frac{2}{3}\times \frac{1}{1}\times \frac{2}{1}$

= 1

উত্তরঃ নির্ণেয় ${\color{DarkGreen} \frac{1-{{\sin }^{2}}30{}^\circ }{1+{{\sin }^{2}}45{}^\circ }\times \frac{{{\cos }^{2}}60{}^\circ +{{\cos }^{2}}30{}^\circ }{\text{cose}{{\text{c}}^{2}}90{}^\circ -{{\cot }^{2}}90{}^\circ }\div \left( \sin 60{}^\circ \tan 30{}^\circ \right)}$ এর মান 1 .

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q6. দেখাই যে,

(i) ${{\sin }^{2}}45{}^\circ +{{\cos }^{2}}45{}^\circ =1$

সমাধান :

বামপক্ষ :

${{\sin }^{2}}45{}^\circ +{{\cos }^{2}}45{}^\circ$

$=\left ( \frac{1}{\sqrt{2}} \right )^{2}+\left ( \frac{1}{\sqrt{2}} \right )^{2}$ ${\color{Blue} \left [ \because sin45^{\circ}=\frac{1}{\sqrt{2}},cos45^{\circ}=\frac{1}{\sqrt{2}} \right ]}$

$=\frac{1}{2}+\frac{1}{2}$

$=\frac{1+1}{2}$

$=\frac{2}{2}$

= 1

ডানপক্ষ :

∴ বামপক্ষ = ডানপক্ষ (প্রমাণিত)

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q6. দেখাই যে,

(ii) $\cos 60{}^\circ ={{\cos }^{2}}30{}^\circ -{{\sin }^{2}}30{}^\circ$

সমাধান :

বামপক্ষ :

$\cos 60{}^\circ$

$=\frac{1}{2}$

ডানপক্ষ :

${{\cos }^{2}}30{}^\circ -{{\sin }^{2}}30{}^\circ$

$=\left ( \frac{\sqrt{3}}{2} \right )^{2}-\left ( \frac{1}{2} \right )^{2}$

$=\frac{3}{4}-\frac{1}{4}$

$=\frac{3-1}{4}$

$=\frac{2}{4}$

$=\frac{1}{2}$

বামপক্ষ = ডানপক্ষ (প্রমাণিত)

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q6. দেখাই যে,

(iii) $\frac{2\tan 30{}^\circ }{1-{{\tan }^{2}}30{}^\circ }=\sqrt{3}$

সমাধান :

বামপক্ষ :

$\frac{2\tan 30{}^\circ }{1-{{\tan }^{2}}30{}^\circ }$

$=\frac{2\times \frac{1}{\sqrt{3}}}{1-\left ( \frac{1}{\sqrt{3}} \right )^{2}}$

$=\frac{\frac{2}{\sqrt{3}}}{1-\frac{1}{3}}$

$=\frac{\frac{2}{\sqrt{3}}}{\frac{3-1}{3}}$

$=\frac{2}{\sqrt{3}}\times \frac{3}{2}$

$=\sqrt{3}$

ডানপক্ষ :

$\sqrt{3}$

বামপক্ষ = ডানপক্ষ (প্রমাণিত)

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q6. দেখাই যে,

(iv) $\sqrt{\frac{1+\cos 30{}^\circ }{1-\cos 30{}^\circ }}=\sec 60{}^\circ +\tan 60{}^\circ$

সমাধান :

বামপক্ষ :

$\sqrt{\frac{1+\cos 30{}^\circ }{1-\cos 30{}^\circ }}$

$=\sqrt{\frac{1+\frac{\sqrt{3}}{2}}{1-\frac{\sqrt{3}}{2}}}$

$=\sqrt{\frac{\frac{2+\sqrt{3}}{2}}{\frac{2-\sqrt{3}}{2}}}$

$=\sqrt{\frac{2+\sqrt{3}}{2}\times \frac{2}{2-\sqrt{3}}}$

$=\sqrt{\frac{\left (2+\sqrt{3} \right )\left (2+\sqrt{3} \right )}{\left (2-\sqrt{3} \right )\left (2+\sqrt{3} \right )}}$

$=\frac{2+\sqrt{3}}{\sqrt{2^{2}-\left ( \sqrt{3} \right )^{2}}}$

$=\frac{2+\sqrt{3}}{ \sqrt{4-3}}$

$=\frac{2+\sqrt{3}}{ \sqrt{1}}$

$=2+\sqrt{3}$

ডানপক্ষ :

$\sec 60{}^\circ +\tan 60{}^\circ$

$=2+\sqrt{3}$

বামপক্ষ = ডানপক্ষ (প্রমাণিত)

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q6. দেখাই যে,

(v) $\frac{2{{\tan }^{2}}30{}^\circ }{1-{{\tan }^{2}}30{}^\circ }+{{\sec }^{2}}45{}^\circ -{{\cot }^{2}}45{}^\circ =\sec 60{}^\circ$

সমাধান :

বামপক্ষ :

$\frac{2{{\tan }^{2}}30{}^\circ }{1-{{\tan }^{2}}30{}^\circ }+{{\sec }^{2}}45{}^\circ -{{\cot }^{2}}45{}^\circ$

$=\frac{2\times \left ( \frac{1}{\sqrt{3}} \right )^{2}}{1-\left ( \frac{1}{\sqrt{3}} \right )^{2}}+\left ( \sqrt{2} \right )^{2}-\left ( 1 \right )^{2}$

$=\frac{\frac{2}{3}}{1-\frac{1}{3}}+2-1$

$=\frac{2}{3}\times \frac{3}{2}+1$

= 1 + 1

= 2

ডানপক্ষ :

$\sec 60{}^\circ$

= 2

বামপক্ষ = ডানপক্ষ (প্রমাণিত)

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q6. দেখাই যে,

(vi) ${{\tan }^{2}}\frac{\pi }{4}\sin \frac{\pi }{3}\tan \frac{\pi }{6}{{\tan }^{2}}\frac{\pi }{3}=1\frac{1}{2}$

সমাধান :

বামপক্ষ :

${{\tan }^{2}}\frac{\pi }{4}\sin \frac{\pi }{3}\tan \frac{\pi }{6}{{\tan }^{2}}\frac{\pi }{3}=1\frac{1}{2}$

$=tan^{2}\frac{180^{\circ}}{4}sin\frac{180^{\circ}}{3}tan\frac{180^{\circ}}{6}tan^{2}\frac{180^{\circ}}{3} {\color{Blue} \left [ \because \pi =180^{\circ} \right ]}$

$=tan^{2}45^{\circ}sin60^{\circ}tan30^{\circ}tan^{2}60^{\circ}$

$=\left ( 1 \right )^{2}\times \frac{\sqrt{3}}{2}\times \frac{1}{\sqrt{3}}\times \left ( \sqrt{3} \right )^{2}$

$=1\times \frac{1}{2}\times 3$

$=\frac{3}{2}$

$=1\frac{1}{2}$

ডানপক্ষ :

$1\frac{1}{2}$

∴ বামপক্ষ = ডানপক্ষ (প্রমাণিত)

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q6. দেখাই যে,

(vii) $\sin \frac{\pi }{3}\tan \frac{\pi }{6}+\sin \frac{\pi }{2}\cos \frac{\pi }{3}=2{{\sin }^{2}}\frac{\pi }{4}$

সমাধান :

বামপক্ষ :

$\sin \frac{\pi }{3}\tan \frac{\pi }{6}+\sin \frac{\pi }{2}\cos \frac{\pi }{3}$

$=sin\frac{180^{\circ}}{3}tan\frac{180^{\circ}}{6}+sin\frac{180^{\circ}}{2}cos\frac{180^{\circ}}{3} {\color{Blue} \left [ \because \pi =180^{\circ} \right ]}$

$=sin60^{\circ}tan30^{\circ}+sin90^{\circ}cos60^{\circ}$

$=\frac{\sqrt{3}}{2}\times \frac{1}{\sqrt{3}}+1\times \frac{1}{2}$

$=\frac{1}{2}+\frac{1}{2}$

= 1

ডানপক্ষ :

$2{{\sin }^{2}}\frac{\pi }{4}$

$=2sin^{2}\left ( \frac{180^{\circ}}{4} \right )$

$=2sin^{2}45^{\circ}$

$=2\times \left ( \frac{1}{\sqrt{2}} \right )^{2} {\color{Blue} \left [ \because sin45^{\circ}=\frac{1}{\sqrt{2}} \right ]}$

$=2\times \frac{1}{2}$

= 1

∴ বামপক্ষ = ডানপক্ষ (প্রমাণিত)

koshe dekhi 23.2 class 10

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q7. (i) $x\sin 45{}^\circ \cos 45{}^\circ \tan 60{}^\circ ={{\tan }^{2}}45{}^\circ -\cos 60{}^\circ$ হলে, $x$ -এর মান নির্ণয় করি।

সমাধান :

প্রদত্ত,

$x\sin 45{}^\circ \cos 45{}^\circ \tan 60{}^\circ ={{\tan }^{2}}45{}^\circ -\cos 60{}^\circ$

বা, $x\times \frac{1}{\sqrt{2}}\times \frac{1}{\sqrt{2}}\times \sqrt{3}=\left ( 1 \right )^{2}-\frac{1}{2}$

বা, $\frac{\sqrt{3}x}{2}=1-\frac{1}{2}$

বা, $\frac{\sqrt{3}x}{2}=\frac{1}{2}$

বা, $\sqrt{3}x=1$

$\therefore x=\frac{1}{\sqrt{3}}$

উত্তরঃ নির্ণেয় x -এর মান ${\color{DarkGreen} \frac{1}{\sqrt{3}}}$ .

koshe dekhi 23.2 class 10

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q7. (ii) $x\sin 60{}^\circ {{\cos }^{2}}30{}^\circ =\frac{{{\tan }^{2}}45{}^\circ \sec 60{}^\circ }{\text{cosec}60{}^\circ }$ হলে, $x$ -এর মান নির্ণয় করি।

সমাধান :

প্রদত্ত,

$x\sin 60{}^\circ {{\cos }^{2}}30{}^\circ =\frac{{{\tan }^{2}}45{}^\circ \sec 60{}^\circ }{\text{cosec}60{}^\circ }$

বা, $x\times \frac{\sqrt{3}}{2}\times \left ( \frac{\sqrt{3}}{2} \right )^{2}=\frac{\left ( 1 \right )^{2}\times 2}{\frac{2}{\sqrt{3}}}$

বা, $\frac{3\sqrt{3}x}{8}=2\times \frac{\sqrt{3}}{2}$

বা, $\frac{3x}{8}=1$

$\therefore x=\frac{8}{3}=2\frac{2}{3}$

উত্তরঃ নির্ণেয় x -এর মান ${\color{DarkGreen} 2\frac{2}{3}}$ .

koshe dekhi 23.2 class 10

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q7. (iii) ${{x}^{2}}={{\sin }^{2}}30{}^\circ +4{{\cot }^{2}}45{}^\circ -{{\sec }^{2}}60{}^\circ$ হলে, $x$ -এর মান নির্ণয় করি।

সমাধান :

প্রদত্ত, ${{x}^{2}}={{\sin }^{2}}30{}^\circ +4{{\cot }^{2}}45{}^\circ -{{\sec }^{2}}60{}^\circ$

বা, $x^{2}=\left ( \frac{1}{2} \right )^{2}+4\left ( 1 \right )^{2}-\left ( 2 \right )^{2}$

বা, $x^{2}=\frac{1}{4}+4-4$

বা, $x^{2}=\frac{1}{4}$

বা, $x=\pm \sqrt{\frac{1}{4}}$

$\therefore x=\frac{1}{2}$

উত্তরঃ নির্ণেয় x -এর মান ${\color{DarkGreen} \frac{1}{2}}$ .

koshe dekhi 23.2 class 10

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q8. $x\tan 30{}^\circ +y\cot 60{}^\circ =0$ এবং $2x-y\tan 45{}^\circ =1$ হলে $x$ ও $y$ এর মান হিসাব করে লিখি।

সমাধান :

প্রদত্ত,

$x\tan 30{}^\circ +y\cot 60{}^\circ =0$

বা, $x\times \frac{1}{\sqrt{3}}+y\times \frac{1}{\sqrt{3}}=0$

বা, $\frac{1}{\sqrt{3}}\left ( x+y \right )=0$

বা, $x+y=0\times \sqrt{3}$

বা, $x+y=0$ ……….(i)

প্রদত্ত,

$2x-y\tan 45{}^\circ =1$

বা, $2x-y\times 1=1 {\color{Blue} \left [ \because tan45^{\circ}=1 \right ]}$

বা, $2x-y=1$ ……….(ii)

(1) নং ও (2) নং সমীকরণ যোগ করে পাই,

$x+y+2x-y=0+1$

বা, 3x = 1

$\therefore x=\frac{1}{3}$

(1) নং সমীকরণে ${\color{Blue} x=\frac{1}{3}}$ বসিয়ে পাই,

$\frac{1}{3}+y=0$

$\therefore y=-\frac{1}{3}$

উত্তরঃ নির্ণেয় ${\color{DarkGreen} x=\frac{1}{3};y=-\frac{1}{3}}$

koshe dekhi 23.2 class 10

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q9. যদি A = B = 45° হয়, তবে যাচাই করি যে,

(i) $\sin \left( A+B \right)=\sin A\cos B+\cos A\sin B$

সমাধান :

বামপক্ষ :

$sin\left ( A+B \right )$

A ও B এর মান (= 45°) বসিয়ে পাই,

$\Rightarrow sin\left ( 45^{\circ}+45^{\circ} \right )$

$=sin90^{\circ}$

$=1\; \; [\because sin90^{\circ}=1]$

ডানপক্ষ :

$sinA.cosB+cosA.sinB$

A ও B এর মান (= 45°) বসিয়ে পাই,

$=sin45^{\circ}.cos45^{\circ}+cos45^{\circ}.sin45^{\circ}$

$=\left ( \frac{1}{\sqrt{2}} \right ).\left ( \frac{1}{\sqrt{2}} \right )+\left ( \frac{1}{\sqrt{2}} \right ).\left ( \frac{1}{\sqrt{2}} \right )\; \; [\because sin45^{\circ}=cos45^{\circ}=\frac{1}{\sqrt{2}}]$

$=\frac{1}{2}+\frac{1}{2}\Rightarrow \frac{1+1}{2}\Rightarrow \frac{2}{2}=1$

${\color{DarkGreen} \therefore \sin \left( A+B \right)=\sin A\cos B+\cos A\sin B}$ (প্রমানিত)

koshe dekhi 23.2 class 10

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q9. যদি A = B = 45° হয়, তবে যাচাই করি যে,

(ii) $\cos \left( A+B \right)=\cos A\cos B-\sin A\sin B$

সমাধান :

বামপক্ষ :

$cos\left ( A+B \right )$

A ও B এর মান (= 45°) বসিয়ে পাই,

$\Rightarrow cos\left ( 45^{\circ}+45^{\circ} \right )$

$=cos90^{\circ}$

$=0\; \; [\because cos90^{\circ}=0]$

ডানপক্ষ :

$cosA.cosB-sinA.sinB$

A ও B এর মান (= 45°) বসিয়ে পাই,

$=cos45^{\circ}.cos45^{\circ}-sin45^{\circ}.sin45^{\circ}$

$=\left ( \frac{1}{\sqrt{2}} \right ).\left ( \frac{1}{\sqrt{2}} \right )-\left ( \frac{1}{\sqrt{2}} \right ).\left ( \frac{1}{\sqrt{2}} \right )\; \; {\color{Blue} [\because sin45^{\circ}=cos45^{\circ}=\frac{1}{\sqrt{2}}]}$

$=\frac{1}{2}-\frac{1}{2}\Rightarrow 0$

∴ ${\color{DarkGreen} \cos \left( A+B \right)=\cos A\cos B-\sin A\sin B}$ (প্রমানিত)

koshe dekhi 23.2 class 10

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q10. (i) ABC সমবাহু ত্রিভুজের BD একটি মধ্যমা। প্রমাণ করি যে, $\tan \angle ABD=\cot \angle BAD$

সমাধান :

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

$\because$ BD হলো সমবাহু $\Delta ABC$ এর মধ্যমা।

∴ $BD \bot AC$ অর্থাৎ $\angle BDA=90^{\circ}$

∴ $\Delta ABD$ এর $\angle BAD+\angle ABD=180^{\circ}-\angle BDA$

অর্থাৎ, $\angle BAD+\angle ABD=180^{\circ}-90^{\circ}\Rightarrow 90^{\circ}$

$\therefore \angle ABD=90^{\circ}-\angle BAD$

এখন, সমকোণী $\Delta ABD$ এর $tan\angle ABD\Rightarrow tan\left ( 90^{\circ}-\angle BAD \right )\; \; [\because \angle ABD=90^{\circ}-\angle BAD]$

${\color{DarkGreen} \therefore tan\angle ABD=cot\angle BAD\; \; \;} {\color{Blue} [\because tan\left ( 90^{\circ}- \theta \right )=cot \theta]}$ (প্রমানিত)

koshe dekhi 23.2 class 10

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q10. (ii) ABC সমদ্বিবাহু ত্রিভুজের AB = AC এবং $\angle BAC={{90}^{\circ }};\angle BAC$ এর সমদ্বিখণ্ডক BC বাহুকে D বিন্দুতে ছেদ করে।

প্রমাণ করি যে, $\frac{sec\angle ACD}{sin\angle CAD}=cosec^{2}\angle CAD$

সমাধান :

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

$\because$ ABC সমদ্বিবাহু ত্রিভুজ এবং AD হলো $\angle BAC$ এর সমদ্বিখণ্ডক।

∴ $AD \bot BC$ অর্থাৎ $\angle ADC=90^{\circ}$

∴ $\Delta ADC$ এর $\angle CAD+\angle ACD=180^{\circ}-\angle ADC\Rightarrow 180^{\circ}-90^{\circ}$

অর্থাৎ, $\angle CAD+\angle ACD=90^{\circ}$

$\angle ACD=90^{\circ}-\angle CAD$

এখন, সমকোণী $\Delta ADC$ এর $\frac{sec\angle ACD}{sin\angle CAD}\Rightarrow \frac{sec\left ( 90^{\circ}-\angle CAD \right )}{sin\angle CAD}\; \; [\because \angle ACD=90^{\circ}-\angle CAD]$

$\Rightarrow \frac{cosec\angle CAD}{sin\angle CAD}\; \; \; [\because sec\left ( 90^{\circ}- \theta)=cosec \theta \right]$

$\Rightarrow cosec^{2}\angle CAD\; \; \; [\because \frac{1}{sin \theta}=cosec \theta]$

∴ ${\color{DarkGreen} \frac{sec\angle ACD}{sin\angle CAD}=cosec^{2}\angle CAD}$ (প্রমানিত)

koshe dekhi 23.2 class 10

ত্রিকোণমিতিক অনুপাত এবং ত্রিকোণমিতিক অভেদাবলি : কষে দেখি - 23.2

Q11. $\theta \left( 0{}^\circ \le \theta \le {{90}^{\circ }} \right)$ -এর কোণ মান/মানগুলির জন্য $2{{\cos }^{2}}\theta -3\cos \theta +1=0$ সত্য হবে নির্ণয় করি।