Koshe Dekhi 5.2 Class 9

রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট)

(Linear Simultaneous Equations)

1. নীচের সমীকরণগুলির লেখচিত্র অঙ্কন করে সমাধানযােগ্য কিনা লিখি ও সমাধানযােগ্য হলে সমাধানটি বা অসংখ্য সমাধানের ক্ষেত্রে 3 টি সমাধান লিখি।

(a) 2x + 3y − 7 = 0

3x + 2y − 8 = 0

সমাধানঃ

2x + 3y − 7 = 0 —– (i)

(i) সমীকরণটির লেখচিত্র অঙ্কন করতে হলে আমাদের কমপক্ষে তিনটি বিন্দুর স্থানাঙ্ক নির্ণয় করতে হবে যা দ্বারা সমীকরণটি সিদ্ধ হয়।

2x + 3y − 7 = 0

বা, 3y = 7 − 2x

∴ y = (7 − 2x) / 3

x	−1	2	8
y	3	1	−3

3x + 2y − 8 = 0 —– (ii)

(ii) সমীকরণটির লেখচিত্র অঙ্কন করতে হলে আমাদের কমপক্ষে তিনটি বিন্দুর স্থানাঙ্ক নির্ণয় করতে হবে যা দ্বারা সমীকরণটি সিদ্ধ হয়।

3x + 2y − 8 = 0

বা, 2y = 8 − 3x

∴ y = (8 − 3x) / 2

x	2	8	14
y	1	−8	−17

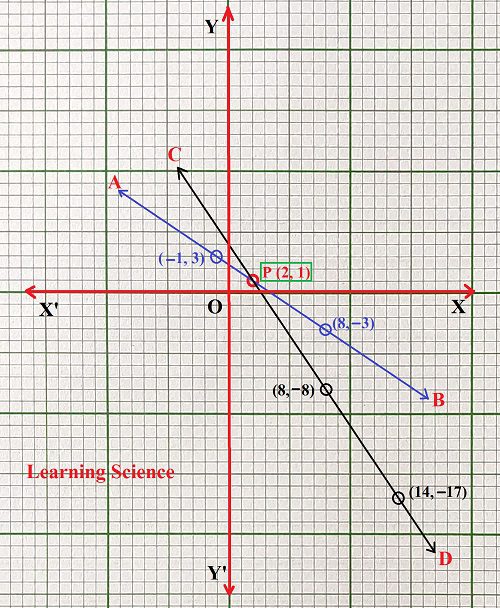
ছককাগজে XOX’ ও YOY’ লম্ব অক্ষ দুটি অঙ্কন করার পরে প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের 1টি বাহুর দৈর্ঘ্য = 1 একক ধরে (i) নং সমীকরণের (−1, 3), (2, 1), (8, −3) বিন্দুগুলি স্থাপন করলাম। এরপর বিন্দুগুলি স্কেলের সাহায্যে যুক্ত করে AB সরলরেখা পেলাম। AB সরলরেখাটি হলো (i) নং সমীকরণের লেখচিত্র।

আবার (i) নং সমীকরণের (2, 1), (8, −8), (14, −17) বিন্দুগুলি স্থাপন করলাম। এরপর বিন্দুগুলি স্কেলের সাহায্যে যুক্ত করে CD সরলরেখা পেলাম। CD সরলরেখাটি হলো (ii) নং সমীকরণের লেখচিত্র।

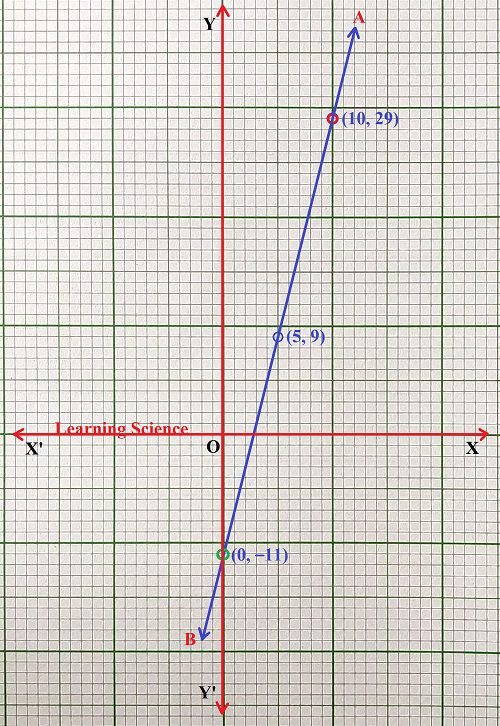
koshe dekhi 5.2 class 9

ওপরের লেখচিত্র থেকে আমি দেখতে পেলাম AB ও CD সরলরেখা দুটি পরস্পরকে P বিন্দুতে ছেদ করেছে।

∴ সমীকরণ দুটি সমাধানযোগ্য।

লেখচিত্র থেকে পেলাম P বিন্দুর স্থানাঙ্ক (2, 1).

∴ সমীকরণ দুটির সাধারণ সমাধান হলো x = 2 এবং y = 1. (Answer)

(b) 4x − y = 11

−8x + 2y = −22

সমাধানঃ

4x − y = 11 —– (i)

4x − y = 11

∴ y = 4x − 11

x	0	5	10
y	−11	9	29

−8x + 2y = −22 —– (ii)

−8x + 2y = −22

বা, 2y = 8x − 22

বা, 2y = 2(4x − 11)

∴ y = 4x − 11

x	0	5	10
y	−11	9	29

ছককাগজে XOX’ ও YOY’ লম্ব অক্ষ দুটি অঙ্কন করার পরে প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের 1টি বাহুর দৈর্ঘ্য = 1 একক ধরে (i) নং ও (ii) নং সমীকরণের (0, −11), (5, 9), (10, 29) বিন্দুগুলি স্থাপন করলাম। এরপর বিন্দুগুলি স্কেলের সাহায্যে যুক্ত করে AB সরলরেখা পেলাম। AB সরলরেখাটি হলো (i) নং ও (ii) নং সমীকরণের লেখচিত্র।

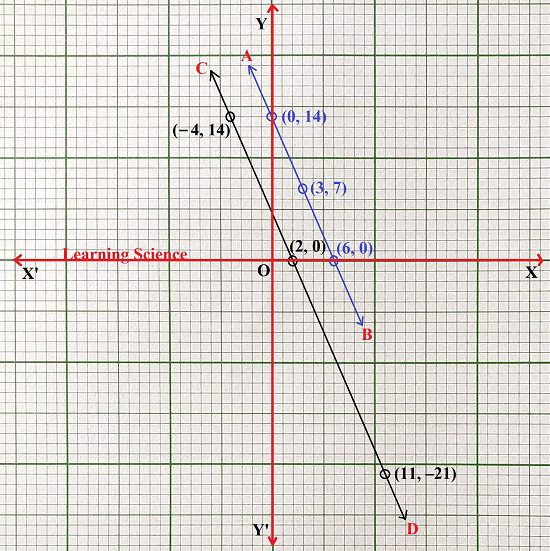
koshe dekhi 5.2 class 9

ওপরের লেখচিত্র থেকে আমি দেখতে পেলাম প্রদত্ত সমীকরণ দুটির জন্য একটি সাধারণ সরলরেখা পেলাম।

∴ সমীকরণ দুটি সমাধানযোগ্য এবং সমীকরণ দুটির অসংখ্য সাধারণ সমাধান পাওয়া যাবে।

∴ সমীকরণ দুটির তিনটি সাধারণ সমাধান হলো

x = 0 এবং y = −11;

x = 5 এবং y = 9;

x = 10 এবং y = 29. (Answer)

21x + 9y = 42

সমাধানঃ

2x + 3y − 7 = 0 —– (i)

7x + 3y = 42

বা, 3y = 42 − 7x

∴ y = (42 − 7x) / 3

x	0	3	6
y	14	7	0

21x + 9y = 42 —– (ii)

21x + 9y = 42

বা, 9y = 42 − 21x

∴ y = (42 − 21x) / 9

x	−4	2	11
y	14	0	−21

ছককাগজে XOX’ ও YOY’ লম্ব অক্ষ দুটি অঙ্কন করার পরে প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের 1টি বাহুর দৈর্ঘ্য = 1 একক ধরে (i) নং সমীকরণের (0, 14), (3, 7), (6, 0) বিন্দুগুলি স্থাপন করলাম। এরপর বিন্দুগুলি স্কেলের সাহায্যে যুক্ত করে AB সরলরেখা পেলাম। AB সরলরেখাটি হলো (i) নং সমীকরণের লেখচিত্র।

আবার (ii) নং সমীকরণের (−4, 14), (2, 0), (11, −21) বিন্দুগুলি স্থাপন করলাম। এরপর বিন্দুগুলি স্কেলের সাহায্যে যুক্ত করে CD সরলরেখা পেলাম। CD সরলরেখাটি হলো (ii) নং সমীকরণের লেখচিত্র।

koshe dekhi 5.2 class 9

ওপরের লেখচিত্র থেকে আমি দেখতে পেলাম AB ও CD সরলরেখা দুটি পরস্পর সমান্তরাল।

∴ সমীকরণ দুটি সমাধানযোগ্য নয়। (Answer)

(d) 5x + y = 13

5x + 5y = 12

সমাধানঃ

5x + y = 13 —– (i)

5x + y = 13

∴ y = (13 − 5x)

x	1	2	3
y	8	3	−2

5x + 5y = 12 —– (ii)

5x + 5y = 12

বা, 5y = 12 − 5x

∴ y = (12 − 5x) / 5

x	$\frac{12}{5}$	0	$\frac{2}{5}$
y	0	$\frac{12}{5}$	2

ছককাগজে XOX’ ও YOY’ লম্ব অক্ষ দুটি অঙ্কন করার পরে প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের 1টি বাহুর দৈর্ঘ্য = $\frac{1}{5}$ একক ধরে (i) নং সমীকরণের (1, 8), (2, 3), (3, −2) বিন্দুগুলি স্থাপন করলাম। এরপর বিন্দুগুলি স্কেলের সাহায্যে যুক্ত করে AB সরলরেখা পেলাম। AB সরলরেখাটি হলো (i) নং সমীকরণের লেখচিত্র।

আবার (ii) নং সমীকরণের $\left (\frac{12}{5},0 \right ),\left ( 0,\frac{12}{5} \right ),\left ( \frac{2}{5},2 \right )$ বিন্দুগুলি স্থাপন করলাম। এরপর বিন্দুগুলি স্কেলের সাহায্যে যুক্ত করে CD সরলরেখা পেলাম। CD সরলরেখাটি হলো (ii) নং সমীকরণের লেখচিত্র।

koshe dekhi 5.2 class 9

∴ সমীকরণ দুটি সমাধানযোগ্য।

লেখচিত্র থেকে পেলাম P বিন্দুর স্থানাঙ্ক $\left ( \frac{53}{20},-\frac{1}{4} \right )$ .

∴ সমীকরণ দুটির সাধারণ সমাধান হলো $x=\frac{53}{20}$ এবং $y=-\frac{1}{4}$ . (Answer)

Koshe Dekhi 5.2 Class 9 Koshe Dekhi 5.2 Class 9

2. নীচের প্রতিজোড়া সমীকরণগুলির একই চলের সহগগুলির ও ধ্রুবকগুলির অনুপাতের সম্পর্ক নির্ণয় করে সমীকরণ দুটি সমাধানযােগ্য কিনা লিখি ও সমীকরণগুলির লেখচিত্র এঁকে যাচাই করি।

(a) x + 5y = 7

x + 5y = 20

সমাধানঃ

x + 5y = 7

∴ x + 5y − 7 = 0 —– (i)

x + 5y = 20

∴ x + 5y − 20 = 0 —– (ii)

এখন, (i) ও (ii) নং সমীকরণের চলের (অর্থাৎ, x ও y) সহগগুলির ও ধ্রুবকগুলির অনুপাতের সম্পর্ক নির্ণয় করি –

$\frac{1}{1}=\frac{5}{5}\neq \frac{-7}{-20}$ ${\color{Blue} \left [ \because \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}} \right ]}$

∴ প্রদত্ত সমীকরণ দুটি সমাধানযোগ্য নয়। (Answer)

এখন আমি লেখচিত্র অঙ্কন করে যাচাই করি –

x + 5y = 7

বা, 5y = 7 − x

∴ y = (7 − x) / 5

x	−3	7	17
y	2	0	−2

x + 5y = 20

বা, 5y = 20 − x

∴ y = (20 − x) / 5

x	0	10	20
y	4	2	0

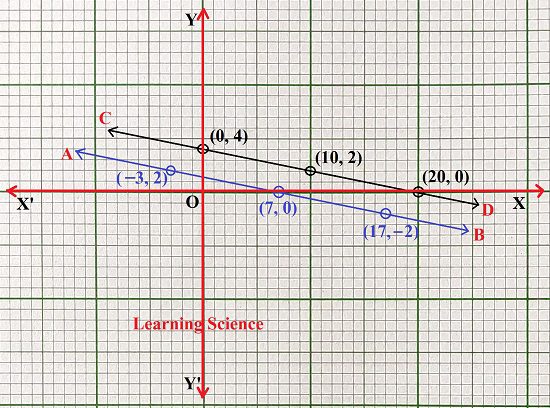
ছককাগজে XOX’ ও YOY’ লম্ব অক্ষ দুটি অঙ্কন করার পরে প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের 1টি বাহুর দৈর্ঘ্য = 1 একক ধরে (i) নং সমীকরণের (−3, 2), (7, 0), (17, −2) বিন্দুগুলি স্থাপন করলাম। এরপর বিন্দুগুলি স্কেলের সাহায্যে যুক্ত করে AB সরলরেখা পেলাম। AB সরলরেখাটি হলো (i) নং সমীকরণের লেখচিত্র।

আবার (ii) নং সমীকরণের (0, 4), (10, 2), (20, 0) বিন্দুগুলি স্থাপন করলাম। এরপর বিন্দুগুলি স্কেলের সাহায্যে যুক্ত করে CD সরলরেখা পেলাম। CD সরলরেখাটি হলো (ii) নং সমীকরণের লেখচিত্র।

koshe dekhi 5.2 class 9

ওপরের লেখচিত্র থেকে আমি দেখতে পেলাম AB ও CD সরলরেখা দুটি পরস্পর সমান্তরাল।

∴ সমীকরণ দুটি সমাধানযোগ্য নয়। (Answer)

(b) 2x + y = 8

2y − 3x = −5

সমাধানঃ

2x + y = 8

∴ 2x + y − 8 = 0 —– (i)

2y − 3x = −5

∴ −3x + 2y + 5 = 0 —– (ii)

$\frac{2}{-3}\neq\frac{1}{2}$ ${\color{Blue} \left [ \because \frac{a_{1}}{a_{2}}\neq\frac{b_{1}}{b_{2}} \right ]}$

∴ প্রদত্ত সমীকরণ দুটি সমাধানযোগ্য এবং সমীকরণ দুটির শুধুমাত্র একটি নিদৃষ্ট সাধারণ সমাধান থাকবে। (Answer)

এখন আমি লেখচিত্র অঙ্কন করে যাচাই করি –

2x + y = 8

∴ y = 8 − 2x

x	0	4	8
y	8	0	−8

2y − 3x = −5

বা, 2y = 3x − 5

∴ y = (3x − 5) / 2

x	1	5	11
y	−1	5	14

ছককাগজে XOX’ ও YOY’ লম্ব অক্ষ দুটি অঙ্কন করার পরে প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের 1টি বাহুর দৈর্ঘ্য = 1 একক ধরে (i) নং সমীকরণের (0, 8), (4, 0), (8, −8) বিন্দুগুলি স্থাপন করলাম। এরপর বিন্দুগুলি স্কেলের সাহায্যে যুক্ত করে AB সরলরেখা পেলাম। AB সরলরেখাটি হলো (i) নং সমীকরণের লেখচিত্র।

আবার (ii) নং সমীকরণের (1, 4), (5, 5), (11, 14) বিন্দুগুলি স্থাপন করলাম। এরপর বিন্দুগুলি স্কেলের সাহায্যে যুক্ত করে CD সরলরেখা পেলাম। CD সরলরেখাটি হলো (ii) নং সমীকরণের লেখচিত্র।

koshe dekhi 5.2 class 9

লেখচিত্র থেকে পেলাম P বিন্দুর স্থানাঙ্ক (3, 2).

∴ সমীকরণ দুটির সাধারণ সমাধান হলো x = 3 এবং y = 2. (Answer)

15x + 24y = 42

সমাধানঃ

5x + 8y = 14

∴ 5x + 8y − 14 = 0 —– (i)

15x + 24y = 42

∴ 15x + 24y − 42 = 0 —– (ii)

$\frac{5}{15}=\frac{8}{24}=\frac{-14}{-42}$ ${\color{Blue} \left [ \because \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}} \right ]}$

∴ প্রদত্ত সমীকরণ দুটি সমাধানযোগ্য এবং সমীকরণ দুটির অসংখ্য সাধারণ সমাধান থাকবে। (Answer)

এখন আমি লেখচিত্র অঙ্কন করে যাচাই করি –

5x + 8y = 14

বা, 8y = 14 − 5x

∴ y = (14 − 5x) / 8

x	−2	6	14
y	3	−2	−7

15x + 24y = 42

বা, 24y = 42 − 15x

বা, 24y = 3(14 − 5x)

বা, 8y = 14 − 5x

∴ y = (14 − 5x) / 8

x	−2	6	14
y	3	−2	−7

ছককাগজে XOX’ ও YOY’ লম্ব অক্ষ দুটি অঙ্কন করার পরে প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের 1টি বাহুর দৈর্ঘ্য = 1 একক ধরে (i) নং ও (ii) নং সমীকরণের (−2, 3), (6, −2), (14, −7) বিন্দুগুলি স্থাপন করলাম। এরপর বিন্দুগুলি স্কেলের সাহায্যে যুক্ত করে AB সরলরেখা পেলাম। AB সরলরেখাটি হলো (i) নং ও (ii) নং সমীকরণের লেখচিত্র।

koshe dekhi 5.2 class 9

(d) 3x + 2y = 6

12x + 8y = 24

সমাধানঃ

3x + 2y = 6

∴ 3x + 2y − 6 = 0 —– (i)

12x + 8y = 24

∴ 12x + 8y − 24 = 0 —– (ii)

$\frac{3}{12}=\frac{2}{8}=\frac{-6}{-24}$ ${\color{Blue} \left [ \because \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}} \right ]}$

এখন আমি লেখচিত্র অঙ্কন করে যাচাই করি –

3x + 2y = 6

বা, 2y = 6 − 3x

∴ y = (6 − 3x) / 8

x	−6	2	10
y	3	0	−3

12x + 8y = 24

বা, 8y = 24 − 12x

বা, 8y = 4(6 − 3x)

বা, 2y = 6 − 3x

∴ y = (6 − 3x) / 8

x	−6	2	10
y	3	0	−3

ছককাগজে XOX’ ও YOY’ লম্ব অক্ষ দুটি অঙ্কন করার পরে প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের 1টি বাহুর দৈর্ঘ্য = 1 একক ধরে (i) নং ও (ii) নং সমীকরণের (−6, 3), (2, 0), (10, −3) বিন্দুগুলি স্থাপন করলাম। এরপর বিন্দুগুলি স্কেলের সাহায্যে যুক্ত করে AB সরলরেখা পেলাম। AB সরলরেখাটি হলো (i) নং ও (ii) নং সমীকরণের লেখচিত্র।

koshe dekhi 5.2 class 9

Koshe Dekhi 5.2 Class 9 Koshe Dekhi 5.2 Class 9

3. নীচের প্রতিজোড়া সমীকরণগুলি একই চলের সহগগুলির ও ধ্রুবকগুলির অনুপাতের সম্পর্ক নির্ণয় করে সমীকরণগুলির লেখচিত্রগুলি সমান্তরাল বা পরস্পরছেদী বা সমাপতিত হবে কিনা লিখি।

(a) 5x + 3y = 11

2x − 7y = −12

সমাধানঃ

5x + 3y = 11

∴ 5x + 3y − 11 = 0 —– (i)

2x − 7y = −12

2x − 7y + 12 = 0 —– (ii)

$\frac{5}{2}\neq \frac{3}{-7}$ ${\color{Blue} \left [ \because \frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}} \right ]}$

∴ প্রদত্ত সমীকরণ দুটির লেখচিত্রগুলি পরস্পরছেদী হবে। (Answer)

(b) 6x − 8y = 2

3x − 4y = 1

সমাধানঃ

6x − 8y = 2

∴ 6x − 8y − 2 = 0 —– (i)

3x − 4y = 1

3x − 4y − 1 = 0 —– (ii)

$\frac{6}{3}=\frac{-8}{-4}=\frac{-2}{-1}$ ${\color{Blue} \left [ \because \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}} \right ]}$

∴ প্রদত্ত সমীকরণ দুটির লেখচিত্রগুলি পরস্পর সমাপতিত হবে। (Answer)

8x − 7y = 56

সমাধানঃ

8x − 7y = 0 —– (i)

8x − 7y = 56

∴ 8x − 7y − 56 = 0 —– (ii)

$\frac{8}{8}=\frac{-7}{-7}\neq \frac{0}{56}$ ${\color{Blue} \left [ \because \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}} \right ]}$

∴ প্রদত্ত সমীকরণ দুটির লেখচিত্রগুলি পরস্পর সমান্তরাল হবে। (Answer)

(d) 4x − 3y = 6

4y − 5x = −7

সমাধানঃ

4x − 3y = 6
∴ 4x − 3y − 6 = 0 —– (i)

4y − 5x = −7

− 5x + 4y + 7 = 0 —– (ii)

$\frac{4}{-5}\neq \frac{-3}{4}$ ${\color{Blue} \left [ \because \frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}} \right ]}$

∴ প্রদত্ত সমীকরণ দুটির লেখচিত্রগুলি পরস্পরছেদী হবে। (Answer)

Koshe Dekhi 5.2 Class 9 Koshe Dekhi 5.2 Class 9

4. নীচের প্রতিজোড়া সমীকরণগুলির মধ্যে যেগুলি সমাধানযােগ্য তাদের লেখচিত্র এঁকে সমাধান করি এবং অসংখ্য সমাধানের ক্ষেত্রে 3টি সমাধান লিখি।

(a) 4x + 3y = 20

8x + 6y = 40

সমাধানঃ

প্রথম অংশ :

4x + 3y = 20

∴ 4x + 3y − 20 = 0 —– (i)

8x + 6y = 40

8x + 6y − 40 = 0 —– (ii)

$\frac{4}{8}=\frac{3}{6}=\frac{-20}{-40}$ ${\color{Blue} \left [ \because \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}= \frac{c_{1}}{c_{2}} \right ]}$

∴ প্রদত্ত সমীকরণ দুটি সমাধানযোগ্য এবং সমীকরণ দুটির অসংখ্য সাধারণ সমাধান থাকবে।

দ্বিতীয় অংশ :

4x + 3y − 20 = 0 —– (i)

বা, 3y = 20 − 4x

∴ y = (20 − 4x) / 3

x	−1	5	11
y	8	0	−8

8x + 6y − 40 = 0 —– (ii)

বা, 6y = 40 − 8x

বা, 6y = 2(20 − 4x)

বা, 3y = 20 − 4x

∴ y = (20 − 4x) / 3

x	−1	5	11
y	8	0	−8

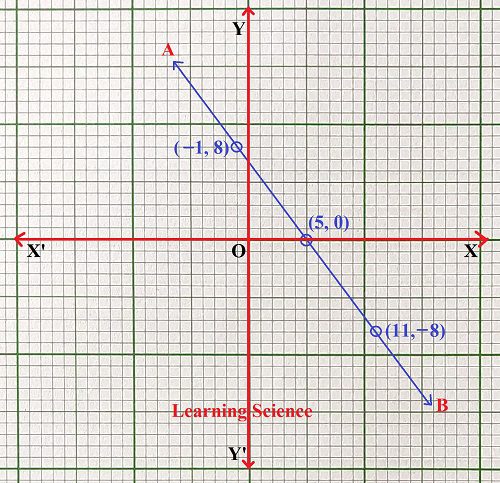
ছককাগজে XOX’ ও YOY’ লম্ব অক্ষ দুটি অঙ্কন করার পরে প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের 1টি বাহুর দৈর্ঘ্য = 1 একক ধরে (i) নং ও (ii) নং সমীকরণের (−1, 8), (5, 0), (11, −8) বিন্দুগুলি স্থাপন করলাম। এরপর বিন্দুগুলি স্কেলের সাহায্যে যুক্ত করে AB সরলরেখা পেলাম। AB সরলরেখাটি হলো (i) নং ও (ii) নং সমীকরণের লেখচিত্র।

koshe dekhi 5.2 class 9

∴ প্রদত্ত সমীকরণ দুটির তিনটি সাধারণ সমাধান হলো নিম্নলিখিত:

(1) x = −1, y = 8;

(2) x = 5, y = 0 এবং

(3) x = 11, y = −8 (Answer)

(b) 4x + 3y = 20

12x + 9y = 20

সমাধানঃ

4x + 3y = 20

∴ 4x + 3y − 20 = 0 —– (i)

12x + 9y = 20

12x + 9y − 20 = 0 —– (ii)

$\frac{4}{12}=\frac{3}{9}\neq \frac{-20}{-20}$ ${\color{Blue} \left [ \because \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}} \right ]}$

∴ প্রদত্ত সমীকরণ দুটি সমাধানযোগ্য নয়। (Answer)

$\fn_cm {\color{Blue} \frac{3x}{4}-\frac{y}{8}=1}$

সমাধানঃ

প্রথম অংশ :

4x + 3y = 20

∴ 4x + 3y − 20 = 0 —– (i)

$\fn_cm \frac{3x}{4}-\frac{y}{8}=1$

বা, $\frac{6x-y}{8}=1$

বা, 6x − y = 8

∴ 6x − y − 8 = 0 —– (ii)

$\frac{4}{6}\neq \frac{3}{-1}$ ${\color{Blue} \left [ \because \frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}} \right ]}$

∴ প্রদত্ত সমীকরণ দুটি সমাধানযোগ্য এবং সমীকরণ দুটির কেবলমাত্র একটি নিদৃষ্ট সাধারণ সমাধান থাকবে।

দ্বিতীয় অংশ :

4x + 3y − 20 = 0 —– (i)

বা, 3y = 20 − 4x

∴ y = (20 − 4x) / 3

x	−1	5	11
y	8	0	−8

6x − y − 8 = 0 —– (ii)

∴ y = 6x − 8

x	0	3	6
y	−8	10	28

ছককাগজে XOX’ ও YOY’ লম্ব অক্ষ দুটি অঙ্কন করার পরে প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের 1টি বাহুর দৈর্ঘ্য = 1 একক ধরে (i) নং সমীকরণের (−1, 8), (5, 0), (11, −8) বিন্দুগুলি স্থাপন করলাম। এরপর বিন্দুগুলি স্কেলের সাহায্যে যুক্ত করে AB সরলরেখা পেলাম। AB সরলরেখাটি হলো (i) নং সমীকরণের লেখচিত্র।

আবার (ii) নং সমীকরণের (0, −8), (3, 10), (6, 28) বিন্দুগুলি স্থাপন করলাম। এরপর বিন্দুগুলি স্কেলের সাহায্যে যুক্ত করে CD সরলরেখা পেলাম। CD সরলরেখাটি হলো (ii) নং সমীকরণের লেখচিত্র।

koshe dekhi 5.2 class 9

লেখচিত্র থেকে পেলাম P বিন্দুর স্থানাঙ্ক (2, 4).

∴ সমীকরণ দুটির নিদৃষ্ট সাধারণ সমাধান হলো x = 2 এবং y = 4. (Answer)

(d) p − q = 3

$\fn_cm {\color{Blue} \frac{p}{3}+\frac{q}{2}=6}$

সমাধানঃ

প্রথম অংশ :

p − q = 3

∴ p − q − 3 = 0 —– (i)

$\fn_cm \frac{p}{3}+\frac{q}{2}=6$

বা, $\frac{2p+3q}{6}=6$

বা, 2p + 3q = 36

∴ 2p + 3q − 36 = 0 —– (ii)

এখন, (i) ও (ii) নং সমীকরণের চলের (অর্থাৎ, p ও q) সহগগুলির ও ধ্রুবকগুলির অনুপাতের সম্পর্ক নির্ণয় করি –

$\frac{1}{2}\neq \frac{-1}{3}$ ${\color{Blue} \left [ \because \frac{a_{1}}{a_{2}}\neq \frac{b_{1}}{b_{2}} \right ]}$

দ্বিতীয় অংশ :

p − q − 3 = 0 —– (i)

∴ q = p − 3

p	0	5	10
q	−3	2	7

2p + 3q − 36 = 0 —– (ii)

বা, 3q = 36 − 2p

∴ q = (36 − 2p) / 3

p	0	6	12
q	12	8	4

ছককাগজে XOX’ ও YOY’ লম্ব অক্ষ দুটি অঙ্কন করার পরে প্রতিটি ক্ষুদ্রতম বর্গক্ষেত্রের 1টি বাহুর দৈর্ঘ্য = 1 একক ধরে (i) নং সমীকরণের (0, −3), (5, 2), (10, 7) বিন্দুগুলি স্থাপন করলাম। এরপর বিন্দুগুলি স্কেলের সাহায্যে যুক্ত করে AB সরলরেখা পেলাম। AB সরলরেখাটি হলো (i) নং সমীকরণের লেখচিত্র।

আবার (ii) নং সমীকরণের (0, 12), (6, 8), (12, 4) বিন্দুগুলি স্থাপন করলাম। এরপর বিন্দুগুলি স্কেলের সাহায্যে যুক্ত করে CD সরলরেখা পেলাম। CD সরলরেখাটি হলো (ii) নং সমীকরণের লেখচিত্র।

koshe dekhi 5.2 class 9

ওপরের লেখচিত্র থেকে আমি দেখতে পেলাম AB ও CD সরলরেখা দুটি পরস্পরকে M বিন্দুতে ছেদ করেছে।

লেখচিত্র থেকে পেলাম M বিন্দুর স্থানাঙ্ক (9, 6).

∴ সমীকরণ দুটির সাধারণ সমাধান হলো p = 9 এবং q = 6. (Answer)

4. (e) p − q = 3

$\fn_cm {\color{Blue} \frac{p}{5}-\frac{q}{5}=3}$

সমাধানঃ

p − q = 3

∴ p − q − 3 = 0 —– (i)

$\fn_cm \frac{p}{5}-\frac{q}{5}=3$

বা, $\frac{p-q}{5}=3$

বা, p − q = 15

∴ p − q − 15 = 0 —– (ii)

$\frac{1}{1}=\frac{-1}{-1}\neq \frac{-3}{-15}$ ${\color{Blue} \left [ \because \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}} \right ]}$

∴ প্রদত্ত সমীকরণ দুটি সমাধানযোগ্য নয়। (Answer)

4. (f) p − q = 3

8p − 8q = 5

সমাধানঃ

p − q = 3

∴ p − q − 3 = 0 —– (i)

8p − 8q = 5

8p − 8q − 5 = 0 —– (ii)

$\frac{1}{8}=\frac{-1}{-8}\neq \frac{-3}{-5}$ ${\color{Blue} \left [ \because \frac{a_{1}}{a_{2}}=\frac{b_{1}}{b_{2}}\neq \frac{c_{1}}{c_{2}} \right ]}$

∴ প্রদত্ত সমীকরণ দুটি সমাধানযোগ্য নয়। (Answer)

Koshe Dekhi 5.2 Class 9 Koshe Dekhi 5.2 Class 9

5. তথাগত একটি দুইচল বিশিষ্ট একঘাত সমীকরণ x + y = 5 লিখেছে। আমি আর একটি দুইচল বিশিষ্ট একঘাত সমীকরণ লিখি যাতে দুটি সমীকরণের লেখচিত্র৷

(a) পরস্পর সমান্তরাল হবে।

(b) পরস্পরছেদি হবে।

সমাধানঃ

(a) x + y = 5 সমীকরণের লেখচিত্রের সাথে সমান্তরাল হবে এমন একটি লেখচিত্রের সমীকরণ হবে 3x + 3y = 30.

(b) x + y = 5 সমীকরণের লেখচিত্রের সাথে পরস্পরছেদি হবে এমন একটি লেখচিত্রের সমীকরণ হবে x − y = 1.

Koshe dekhi 5.2 class 9

রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট)

(Linear Simultaneous Equations)

Support Me

If you like my work then you can Support me by contributing a small amount which will help me a lot to grow my Website. It’s a request to all of you. You can donate me through phone pay / Paytm/ Gpay on this number 7980608289 or by the link below :

and visit Our website : learningscience.co.in

গণিত প্রকাশ (দশম শ্রেণী) সম্পূর্ণ সমাধান

গণিত প্রকাশ (নবম শ্রেণী) সম্পূর্ণ সমাধান

গণিত প্রভা (ষষ্ঠ শ্রেণী) সম্পূর্ণ সমাধান

জীবন বিজ্ঞান (দশম শ্রেণী) (Life Science)

Thank You

Koshe Dekhi 5.2 Class 9 Koshe Dekhi 5.2 Class 9 Koshe Dekhi 5.2 Class 9 Koshe Dekhi 5.2 Class 9 Koshe Dekhi 5.2 Class 9 Koshe Dekhi 5.2 Class 9 Koshe Dekhi 5.2 Class 9 Koshe Dekhi 5.2 Class 9 Koshe Dekhi 5.2 Class 9 Koshe Dekhi 5.2 Class 9 Koshe Dekhi 5.2 Class 9 Koshe Dekhi 5.2 Class 9 Koshe Dekhi 5.2 Class 9 Koshe Dekhi 5.2 Class 9 Koshe Dekhi 5.2 Class 9 Koshe Dekhi 5.2 Class 9 Koshe Dekhi 5.2 Class 9 Koshe Dekhi 5.2 Class 9 Koshe Dekhi 5.2 Class 9

Koshe Dekhi 5.2 Class 9

Koshe Dekhi 5.2 Class 9

Support Me

Leave a Comment Cancel reply