Koshe dekhi 5.3 class 9

রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) : Koshe dekhi - 5.3

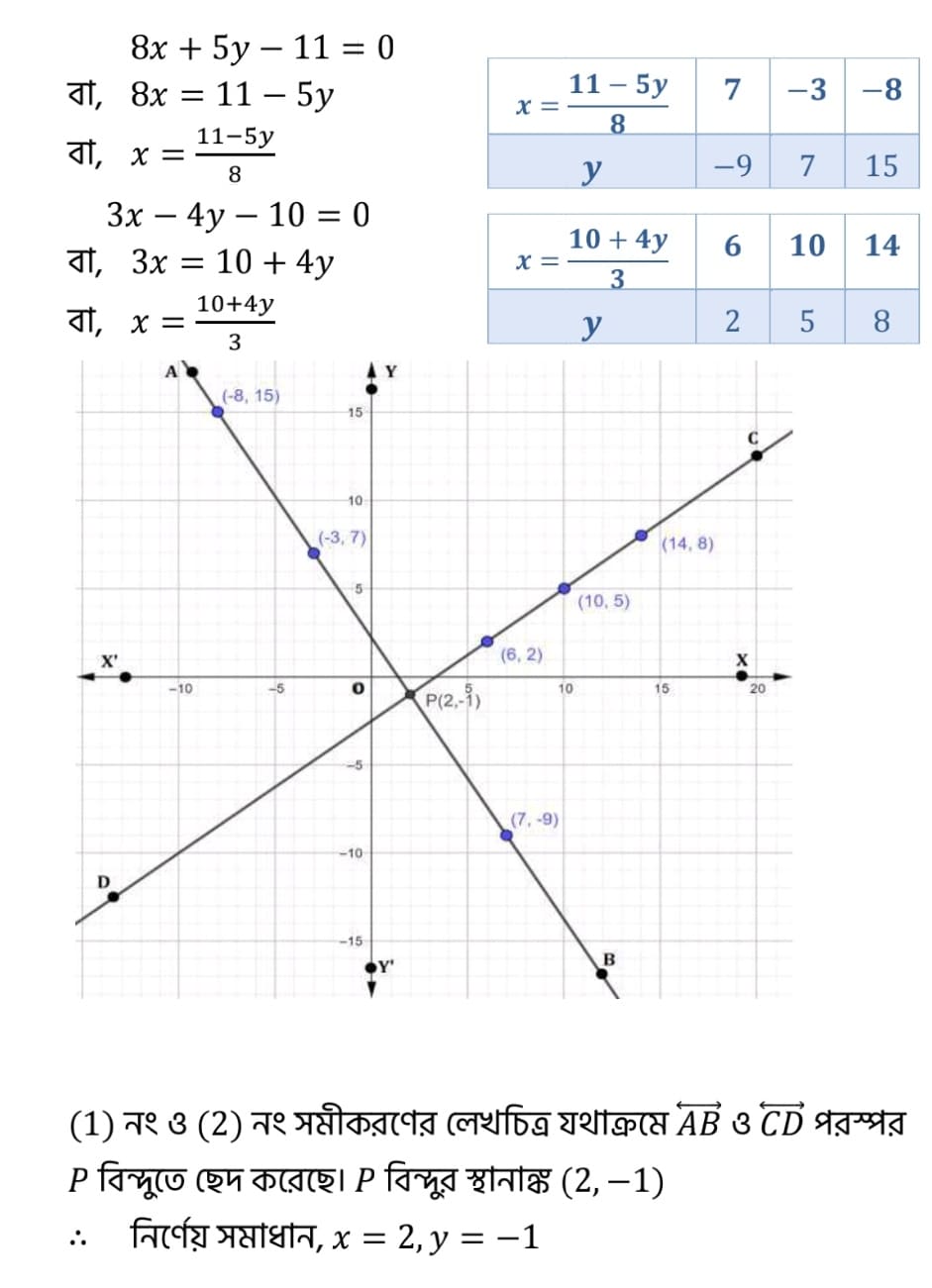
1. নীচের দুইচলবিশিষ্ট একঘাত সমীকরণগুলি অপনয়ন পদ্ধতিতে সমাধান করি ও লেখচিত্রের সাহায্যে সমাধান করে যাচাই করি।

(a) $\fn_cm {\color{Blue} 8x+5y-11=0}$

$\fn_cm {\color{Blue} 3x-4y-10=0}$

অপনয়ন পদ্ধতিতে সমাধানঃ

$\fn_cm 8x+5y-11=0$

বা, $\fn_cm 8x+5y=11 .....\left ( i \right )$

এবং,

$\fn_cm 3x-4y-10=0$

বা, $\fn_cm 3x-4y=10......\left ( ii \right )$

(i) নং সমীকরণকে 3 দ্বারা এবং (ii) নং সমীকরণকে 8 দ্বারা গুন্ করে পাই,

$\small 24x+15y=33$ ……(iii)

$\small 24x-32y=80$ ……(iv)

(iii) নং সমীকরণ থেকে (iv) নং সমীকরণ বিয়োগ করে পাই,

$\small 24x+15y-24x+32y=33-80$

বা, $\small 47y=-47$

$\small \therefore y=\frac{-47}{47}=-1$

y এর মান (i) নং সমীকরণে বসিয়ে পাই,

$\small 8x+5\times \left ( -1 \right )=11$

বা, $\small 8x=11+5$

বা, $\small x=\frac{16}{8}$

$\small \therefore x=2$

নির্ণেয় সমীকরণের সমাধান x = 2 ও y = -1

লেখচিত্রের সাহায্যে সমাধান :

Koshe dekhi 5.3 class 9

রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) : Koshe dekhi - 5.3

(b) $\fn_cm {\color{Blue} 2x+3y-7=0}$

$\fn_cm {\color{Blue} 3x+2y-8=0}$

সমাধানঃ

$\fn_cm 2x+3y-7=0$

বা, $\fn_cm 2x+3y=7$ …..(i)

এবং,

$\fn_cm 3x+2y-8=0$

বা, $\fn_cm 3x+2y=8$ ……(ii)

(i) নং সমীকরণকে 3 দ্বারা এবং (ii) নং সমীকরণকে 2 দ্বারা গুন্ করে পাই,

$\fn_cm 6x+9y=21$ ……(iii)

$\fn_cm 6x+4y=16$ ……(iv)

(iii) নং সমীকরণ থেকে (iv) নং সমীকরণ বিয়োগ করে পাই,

$\fn_cm 6x+9y-6x-4y=21-16$

বা, $\small 5y=5$

বা, $\small y=\frac{5}{5}$

$\small \therefore y=1$

y এর মান (i) নং সমীকরণে বসিয়ে পাই,

$\small 2x+3\times 1=7$

বা, $\small 2x=7-3$

বা, $\small x=\frac{4}{2}$

$\small \therefore x=2$

নির্ণেয় সমীকরণের সমাধান x = 2 ও y = 1

লেখচিত্রের সাহায্যে সমাধান :

Koshe Dekhi 5.3 class 9

Koshe dekhi 5.3 class 9

রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) : Koshe dekhi - 5.3

2. $\fn_cm {\color{Blue} 7x-5y+2=0}$ সমীকরণকে কত দিয়ে গুণ করে $\fn_cm {\color{Blue} 2x+15y+3=0}$ সমীকরণের সঙ্গে যােগ করব। যাতে y চলটিকে অপনীত করতে পারি।

সমাধানঃ

$\fn_cm 7x-5y+2=0$ সমীকরণকে 3 দিয়ে গুণ করে $\fn_cm 2x+15y+3=0$ সমীকরণের সঙ্গে যােগ করলে y চলটিকে অপনীত করা যাবে।

Koshe dekhi 5.3 class 9

রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) : Koshe dekhi - 5.3

3. $\fn_cm {\color{Blue} 4x-3y=16}$ ও $\fn_cm {\color{Blue} 6x+5y=62}$ উভয় সমীকরণকে সবথেকে ছােটো কোন কোন স্বাভাবিক সংখ্যা দিয়ে গুণ করলে দুটি সমীকরণের x-এর সহগ সমান হবে তা লিখি।

সমাধানঃ

$\fn_cm 4x-3y=16$

বা, $\fn_cm 4x\times 3-3y\times 3=16\times 3$

বা, $\fn_cm 12x-9y=48$

আবার,

$\fn_cm 6x+5y=62$

বা, $\fn_cm 6x\times 2+5y\times 2=62\times 2$

বা, $\fn_cm 12x+10y=124$

$\fn_cm {\color{DarkGreen} 4x-3y=16}$ সমীকরণকে সবথেকে ছােটো 3 দিয়ে গুণ করলে ও $\fn_cm {\color{DarkGreen} 6x+5y=62}$ সমীকরণকে সবথেকে ছােটো 2 দিয়ে গুণ করলে দুটি সমীকরণের x-এর সহগ সমান হবে।

Koshe dekhi 5.3 class 9

রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) : Koshe dekhi - 5.3

4. নীচের দুইচলবিশিষ্ট সমীকরণগুলি অপনয়ন পদ্ধতিতে সমাধান করি।

(i) $\fn_cm {\color{Blue} 3x+2y=6}$

$\fn_cm {\color{Blue} 2x-3y=17}$

সমাধানঃ

$3x+2y=6$ …..(i)

$2x-3y=17$ ….(ii)

(i) নং সমীকরণকে 2 দ্বারা এবং (ii) নং সমীকরণকে 3 দ্বারা গুন্ করে পাই,

$\fn_cm 6x+4y=12$ ……(iii)

$\fn_cm 6x-9y=51$ ……(iv)

(iii) নং সমীকরণ থেকে (iv) নং সমীকরণ বিয়োগ করে পাই,

$\fn_cm 6x+4y-6x+9y=12-51$

বা, $13y=-39$

বা, $y=-\frac{39}{13}$

$\small \therefore y=-3$

y এর মান (i) নং সমীকরণে বসিয়ে পাই,

$\small 3x+2\times \left (-3 \right )=6$

বা, $3x=6+6$

বা, $\small x=\frac{12}{3}$

$\small \therefore x=4$

নির্ণেয় সমীকরণের সমাধান x = 4 ও y = -3

Koshe dekhi 5.3 class 9

রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) : Koshe dekhi - 5.3

4. নীচের দুইচলবিশিষ্ট সমীকরণগুলি অপনয়ন পদ্ধতিতে সমাধান করি।

(ii) $\fn_cm {\color{Blue} 2x+3y=32}$

$\fn_cm {\color{Blue} 11y-9x=3}$

সমাধানঃ

$2x+3y=32$ ……(i)

$-9x+11y=3$ …….(ii)

(i) নং সমীকরণকে 11 দ্বারা এবং (ii) নং সমীকরণকে 3 দ্বারা গুন্ করে পাই,

$22x+33y=352$ ……(iii)

$-27x+33y=9$ ……(iv)

(iii) নং সমীকরণ থেকে (iv) নং সমীকরণ বিয়োগ করে পাই,

$22x+33y+27x-33y=352-9$

বা, $49x=343$

বা, $x=\frac{343}{49}$

$\small \therefore x=7$

x এর মান (i) নং সমীকরণে বসিয়ে পাই,

$\small 2\times 7+3y=32$

বা, $3y=32-14$

বা, $\small y=\frac{18}{3}$

$\small \therefore y=6$

নির্ণেয় সমীকরণের সমাধান x = 7 ও y = 6

Koshe dekhi 5.3 class 9

রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) : Koshe dekhi - 5.3

4. নীচের দুইচলবিশিষ্ট সমীকরণগুলি অপনয়ন পদ্ধতিতে সমাধান করি।

(iii) $\fn_cm {\color{Blue} x+y=48}$

$\fn_cm {\color{Blue} x+4=\frac{5}{2}\left ( y+4 \right )}$

সমাধানঃ

$\fn_cm x+y=48$ ……(i)

$\fn_cm x+4=\frac{5}{2}\left ( y+4 \right )$

বা, $2x+8=5y+20$

বা, $2x-5y=20-8$

বা, $2x-5y=12$ …….(ii)

(i) নং সমীকরণকে 2 দ্বারা এবং (ii) নং সমীকরণকে 1 দ্বারা গুন্ করে পাই,

$2x+2y=96$ ……(iii)

$2x-5y=12$ ……(iv)

(iii) নং সমীকরণ থেকে (iv) নং সমীকরণ বিয়োগ করে পাই,

$2x+2y-2x+5y=96-12$

বা, $7y=84$

বা, $y=\frac{84}{7}$

$\small \therefore y=12$

y এর মান (i) নং সমীকরণে বসিয়ে পাই,

$x+12=48$

বা, $x=48-12$

$\small \therefore x=36$

নির্ণেয় সমীকরণের সমাধান x = 36 ও y = 12

Koshe dekhi 5.3 class 9

রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) : Koshe dekhi - 5.3

4. নীচের দুইচলবিশিষ্ট সমীকরণগুলি অপনয়ন পদ্ধতিতে সমাধান করি।

(iv) $\fn_cm {\color{Blue} \frac{x}{2}+\frac{y}{3}=8}$

$\fn_cm {\color{Blue} \frac{5x}{4}-3y=-3}$

সমাধানঃ

$\fn_cm \frac{x}{2}+\frac{y}{3}=8$

বা, $\frac{3x+2y}{6}=8$

বা, $3x+2y=48$ ……(i)

$\fn_cm \frac{5x}{4}-3y=-3$

বা, $\frac{5x-12y}{4}=-3$

বা, $5x-12y=-12$ …….(ii)

(i) নং সমীকরণকে 5 দ্বারা এবং (ii) নং সমীকরণকে 3 দ্বারা গুন্ করে পাই,

$15x+10y=240$ ……(iii)

$15x-36y=-36$ ……(iv)

(iii) নং সমীকরণ থেকে (iv) নং সমীকরণ বিয়োগ করে পাই,

$15x+10y-15x+36y=240+36$

বা, $46y=276$

বা, $y=\frac{276}{46}$

$\small \therefore y=6$

y এর মান (i) নং সমীকরণে বসিয়ে পাই,

$3x+2\times 6=48$

বা, $3x=48-12$

বা, $x=\frac{36}{3}$

$\small \therefore x=12$

নির্ণেয় সমীকরণের সমাধান x = 12 ও y = 6

Koshe dekhi 5.3 class 9

রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) : Koshe dekhi - 5.3

4. নীচের দুইচলবিশিষ্ট সমীকরণগুলি অপনয়ন পদ্ধতিতে সমাধান করি।

(v) $\fn_cm {\color{Blue} 3x-\frac{2}{y}=5}$

$\fn_cm {\color{Blue} x+\frac{4}{y}=4}$

সমাধানঃ

$\fn_cm 3x-\frac{2}{y}=5$

বা, $\frac{3xy-2}{y}=5$

বা, $3xy-2=5y$

বা, $3xy-5y=2$ …….(i)

এবং

$\fn_cm x+\frac{4}{y}=4$

বা, $\frac{xy+4}{y}=4$

বা, $xy+4=4y$

বা, $xy-4y=-4$ ……(ii)

(i) নং সমীকরণকে 1 দ্বারা এবং (ii) নং সমীকরণকে 3 দ্বারা গুন্ করে পাই,

$3xy-5y=2$ ……(iii)

$3xy-12y=-12$ ……(iv)

(iii) নং সমীকরণ থেকে (iv) নং সমীকরণ বিয়োগ করে পাই,

$3xy-5y-3xy+12y=2+12$

বা, $7y=14$

বা, $y=\frac{14}{7}$

$\small \therefore y=2$

y এর মান (i) নং সমীকরণে বসিয়ে পাই,

$3x\times 2-5\times 2=2$

বা, $6x=2+10$

বা, $x=\frac{12}{6}$

$\small \therefore x=2$

নির্ণেয় সমীকরণের সমাধান x = 2 ও y = 2

Koshe dekhi 5.3 class 9

রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) : Koshe dekhi - 5.3

4. নীচের দুইচলবিশিষ্ট সমীকরণগুলি অপনয়ন পদ্ধতিতে সমাধান করি।

(vi) $\fn_cm {\color{Blue} \frac{x}{2}+\frac{y}{3}=1}$

$\fn_cm {\color{Blue} \frac{x}{3}+\frac{y}{2}=1}$

সমাধানঃ

$\fn_cm \frac{x}{2}+\frac{y}{3}=1$

বা, $\frac{3x+2y}{6}=1$

বা, $3x+2y=6$ …….(i)

এবং

$\fn_cm \frac{x}{3}+\frac{y}{2}=1$

বা, $\frac{2x+3y}{6}=1$

বা, $2x+3y=6$ …….(ii)

(i) নং সমীকরণকে 2 দ্বারা এবং (ii) নং সমীকরণকে 3 দ্বারা গুন্ করে পাই,

$6x+4y=12$ ……(iii)

$6x+9y=18$ ……(iv)

(iii) নং সমীকরণ থেকে (iv) নং সমীকরণ বিয়োগ করে পাই,

$6x+4y-6x-9y=12-18$

বা, $-5y=-6$

$\therefore y=\frac{6}{5}$

y এর মান (i) নং সমীকরণে বসিয়ে পাই,

$3x+2\times \frac{6}{5}=6$

বা, $3x=6-\frac{12}{5}$

বা, $3x=\frac{30-12}{5}$

$x=\frac{18}{5\times 3}$

$\therefore x=\frac{6}{5}$

নির্ণেয় সমীকরণের সমাধান ${\color{DarkGreen} x=\frac{6}{5}}$ ও ${\color{DarkGreen} y=\frac{6}{5}}$

Koshe dekhi 5.3 class 9

রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) : Koshe dekhi - 5.3

4. নীচের দুইচলবিশিষ্ট সমীকরণগুলি অপনয়ন পদ্ধতিতে সমাধান করি।

(vii) $\fn_cm {\color{Blue} \frac{x+y}{2}+\frac{3x-5y}{4}=2}$

$\fn_cm {\color{Blue} \frac{x}{14}+\frac{y}{18}=1}$

সমাধানঃ

$\fn_cm \frac{x+y}{2}+\frac{3x-5y}{4}=2$

বা, $\frac{2x+2y+3x-5y}{4}=2$

বা, $5x-3y=8$ …….(i)

এবং

$\fn_cm \frac{x}{14}+\frac{y}{18}=1$

বা, $\frac{9x+7y}{126}=1$

বা, $9x+7y=126$ …….(ii)

(i) নং সমীকরণকে 9 দ্বারা এবং (ii) নং সমীকরণকে 5 দ্বারা গুন্ করে পাই,

$45x-27y=72$ ……(iii)

$45x+35y=630$ ……(iv)

(iii) নং সমীকরণ থেকে (iv) নং সমীকরণ বিয়োগ করে পাই,

$45x-27y-45x-35y=72-630$

বা, $-62y=-558$

বা, $y=\frac{-558}{-62}$

$\therefore y=9$

y এর মান (i) নং সমীকরণে বসিয়ে পাই,

$5x-3\times 9=8$

বা, $5x=27+8$

বা, $5x=35$

বা, $x=\frac{35}{5}$

$\therefore x=7$

নির্ণেয় সমীকরণের সমাধান x = 7 ও y = 9

Koshe dekhi 5.3 class 9

রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) : Koshe dekhi - 5.3

4. নীচের দুইচলবিশিষ্ট সমীকরণগুলি অপনয়ন পদ্ধতিতে সমাধান করি।

(viii) $\fn_cm {\color{Blue} \frac{xy}{x+y}=\frac{1}{5}}$

$\fn_cm {\color{Blue} \frac{xy}{x-y}=\frac{1}{9}}$

সমাধানঃ

$\fn_cm \frac{xy}{x+y}=\frac{1}{5}$

বা, $x+y=5xy$ …….(i)

এবং

$\fn_cm \frac{xy}{x-y}=\frac{1}{9}$

বা, $x-y=9xy$ …….(ii)

(i) নং সমীকরণ থেকে (ii) নং সমীকরণ বিয়োগ করে পাই,

$x+y-x+y=5xy-9xy$

বা, $2y=-4xy$

বা, $2=-4x$

বা, $x=\frac{2}{-4}$

$\therefore x=-\frac{1}{2}$

x এর মান (i) নং সমীকরণে বসিয়ে পাই,

$-\frac{1}{2}+y=5\times \left ( -\frac{1}{2} \right )y$

বা, $y+\frac{5y}{2}=\frac{1}{2}$

বা, $\frac{2y+5y}{2}=\frac{1}{2}$

বা, $\frac{7y}{2}=\frac{1}{2}$

বা, $7y=1$

$\therefore y=\frac{1}{7}$

নির্ণেয় সমীকরণের সমাধান ${\color{DarkGreen} x=-\frac{1}{2}}$ ও ${\color{DarkGreen} y=\frac{1}{7}}$

Koshe dekhi 5.3 class 9

রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) : Koshe dekhi - 5.3

4. নীচের দুইচলবিশিষ্ট সমীকরণগুলি অপনয়ন পদ্ধতিতে সমাধান করি।

(ix) $\fn_cm {\color{Blue} \frac{1}{x-1}+\frac{1}{y-2}=3}$

$\fn_cm {\color{Blue} \frac{2}{x-1}+\frac{3}{y-2}=5}$

সমাধানঃ

$\fn_cm \frac{1}{x-1}+\frac{1}{y-2}=3$

ধরি, $\frac{1}{x-1}=a$ এবং $\frac{1}{y-2}=b$

∴ a + b = 3 …….(i)

আবার,

$\fn_cm \frac{2}{x-1}+\frac{3}{y-2}=5$

বা, 2a + 3b = 5 …….(ii)

(i) নং সমীকরণকে 2 দ্বারা এবং (ii) নং সমীকরণকে 1 দ্বারা গুন্ করে পাই,

2a + 2b = 6 . ……(iii)

2a + 3b = 5 . ……(iv)

(iii) নং সমীকরণ থেকে (iv) নং সমীকরণ বিয়োগ করে পাই,

2a + 2b – 2a – 3b = 6 – 5

বা, – b = 1

∴ b = – 1

b এর মান (i) নং সমীকরণে বসিয়ে পাই,

a – 1 = 3

বা, a = 3 + 1

∴ a = 4

এখন,

$\frac{1}{y-2}=b$

বা, $\frac{1}{y-2}=-1$

বা, – y + 2 = 1

বা, – y = 1 – 2

বা, – y = – 1

∴ y = 1

$\frac{1}{x-1}=a$

বা, $\frac{1}{x-1}=4$

বা, 4x – 4 = 1

বা, 4x = 1 + 4

বা, 4x = 5

$\therefore x=\frac{5}{4}=1\frac{1}{4}$

নির্ণেয় সমীকরণের সমাধান ${\color{DarkGreen} x=1\frac{1}{4}}$ ও y = 1

Koshe dekhi 5.3 class 9

রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) : Koshe dekhi - 5.3

4. নীচের দুইচলবিশিষ্ট সমীকরণগুলি অপনয়ন পদ্ধতিতে সমাধান করি।

(x) $\fn_cm {\color{Blue} \frac{14}{x+y}+\frac{3}{x-y}=5}$

$\fn_cm {\color{Blue} \frac{21}{x+y}-\frac{1}{x-y}=2}$

সমাধানঃ

$\fn_cm \frac{14}{x+y}+\frac{3}{x-y}=5$

ধরি, $\frac{1}{x+y}=a$ এবং $\frac{1}{x-y}=b$

∴ 14a + 3b = 5 …….(i)

আবার,

$\fn_cm \frac{21}{x+y}-\frac{1}{x-y}=2$

বা, 21a – b = 2 …….(ii)

(i) নং সমীকরণকে 1 দ্বারা এবং (ii) নং সমীকরণকে 3 দ্বারা গুন্ করে পাই,

14a + 3b = 5 . ……(iii)

63a – 3b = 6 . ……(iv)

(iii) নং সমীকরনের সাথে (iv) নং সমীকরণ যোগ করে পাই,

14a + 3b + 63a – 3b= 5 + 6

বা, 77a = 11

$a=\frac{11}{77}$

$\therefore a=\frac{1}{7}$

a এর মান (i) নং সমীকরণে বসিয়ে পাই,

$14\times \frac{1}{7}+3b=5$

বা, 2 + 3b = 5

বা, 3b = 5 – 2

বা, 3b = 3

বা, $b=\frac{3}{3}$

∴ b = 1

এখন,

$\frac{1}{x+y}=a$

বা, $\frac{1}{x+y}=\frac{1}{7}$

বা, x + y = 7 ……(v)

$\frac{1}{x-y}=b$

বা, $\frac{1}{x-y}=1$

বা, x – y = 1 …….(vi)

(v) নং সমীকরনের সাথে (vi) নং সমীকরণ যোগ করে পাই,

x + y + x – y = 7 + 1

বা, 2x = 8

বা, $x=\frac{8}{2}$

$\therefore x=4$

x এর মান (v) নং সমীকরণে বসিয়ে পাই,

4 + y = 7

∴ y = 7 – 4 = 3

নির্ণেয় সমীকরণের সমাধান x = 4 ও y = 3

Koshe dekhi 5.3 class 9

রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) : Koshe dekhi - 5.3

4. নীচের দুইচলবিশিষ্ট সমীকরণগুলি অপনয়ন পদ্ধতিতে সমাধান করি।

(xi) $\fn_cm {\color{Blue} \frac{x+y}{5}-\frac{x-y}{4}=\frac{7}{20}}$

$\fn_cm {\color{Blue} \frac{x+y}{3}-\frac{x-y}{2}+\frac{5}{6}=0}$

সমাধানঃ

$\fn_cm \frac{x+y}{5}-\frac{x-y}{4}=\frac{7}{20}$

বা, $\frac{4x+4y-5x+5y}{20}=\frac{7}{20}$

বা, $\frac{-x+9y}{20}=\frac{7}{20}$

বা, $-x+9y=7$ ……(i)

$\fn_cm \frac{x+y}{3}-\frac{x-y}{2}+\frac{5}{6}=0$

বা, $\frac{2x+2y-3x+3y}{6}=-\frac{5}{6}$

বা, $\frac{-x+5y}{6}=-\frac{5}{6}$

বা, $-x+5y=-5$

বা, $x-5y=5$ ……(ii)

(i) নং সমীকরণের সাথে (ii) নং সমীকরণ যোগ করে পাই,

− x + 9y + x – 5y = 7 + 5

বা, 4y = 12

বা, $y=\frac{12}{4}$

∴ y = 3

y এর মান (ii) নং সমীকরণে বসিয়ে পাই,

$x-5\times 3=5$

বা, x = 5 + 15

∴ x = 20

নির্ণেয় সমীকরণের সমাধান x = 20 ও y = 3

Koshe dekhi 5.3 class 9

রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) : Koshe dekhi - 5.3

4. নীচের দুইচলবিশিষ্ট সমীকরণগুলি অপনয়ন পদ্ধতিতে সমাধান করি।

(xii) $\fn_cm {\color{Blue} x+y=a+b}$

$\fn_cm {\color{Blue} ax-by=a^{2}-b^{2}}$

সমাধানঃ

$\fn_cm x+y=a+b$ ……(i)

$\fn_cm ax-by=a^{2}-b^{2}$ (ii)

(i) নং সমীকরণকে a দ্বারা গুন্ করে পাই,

$ax+ay=a^{2}+ab$ ……(iii)

(iii) নং সমীকরণ থেকে (ii) নং সমীকরণ বিয়োগ করে পাই,

$ax+ay-ax+by=a^{2}+ab-a^{2}+b^{2}$

বা, $ay+by=ab+b^{2}$

বা, $y\left ( a+b \right )=b\left ( a+b \right )$

∴ y = b

y এর মান (i) নং সমীকরণে পাই,

x + b = a + b

বা, x = a + b – b

∴ x = a

নির্ণেয় সমীকরণের সমাধান x = a ও y = b

Koshe dekhi 5.3 class 9

রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) : Koshe dekhi - 5.3

4. নীচের দুইচলবিশিষ্ট সমীকরণগুলি অপনয়ন পদ্ধতিতে সমাধান করি।

(xiii) $\fn_cm {\color{Blue} \frac{x+a}{a}=\frac{y+b}{b}}$

$\fn_cm {\color{Blue} ax-by=a^{2}-b^{2}}$

সমাধানঃ

$\fn_cm \frac{x+a}{a}=\frac{y+b}{b}$

বা, bx +ab = ay + ab

বা, bx – ay = ab – ab

বা, bx – ay = 0 ……..(i)

$\fn_cm ax-by=a^{2}-b^{2}$ …….(ii)

(i) নং সমীকরণকে a দ্বারা এবং (ii) নং সমীকরণকে b দ্বারা গুন্ করে পাই,

$abx-a^{2}y=0$ …….(iii)

$abx-b^{2}y=a^{2}b-b^{3}$ ……(iv)

(iii) নং সমীকরণ থেকে (ii) নং সমীকরণ বিয়োগ করে পাই,

$abx-a^{2}y-abx+b^{2}y=0-a^{2}b+b^{3}$

বা, $y\left ( b^{2}-a^{2} \right )=b\left ( b^{2}-a^{2} \right )$

∴ y = b

y এর মান (i) নং সমীকরণে পাই,

bx – a × b = 0

বা, bx = ab

∴ x = a

নির্ণেয় সমীকরণের সমাধান x = a ও y = b

Koshe dekhi 5.3 class 9

রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) : Koshe dekhi - 5.3

4. নীচের দুইচলবিশিষ্ট সমীকরণগুলি অপনয়ন পদ্ধতিতে সমাধান করি।

(xiv) $\fn_cm {\color{Blue} ax+by=c}$

$\fn_cm {\color{Blue} a^{2}x+b^{2}y=c^{2}}$

সমাধানঃ

$\fn_cm ax+by=c$ ……(i)

$\fn_cm a^{2}x+b^{2}y=c^{2}$ …….(ii)

(i) নং সমীকরণকে a দ্বারা এবং (ii) নং সমীকরণকে 1 দ্বারা গুন্ করে পাই,

$\fn_cm a^{2}x+aby=ac$ …….(iii)

$\fn_cm a^{2}x+b^{2}y=c^{2}$ ……(iv)

(iii) নং সমীকরণ থেকে (iv) নং সমীকরণ বিয়োগ করে পাই,

$\fn_cm a^{2}x+aby-a^{2}x-b^{2}y=ac-c^{2}$

বা, $\fn_cm aby-b^{2}y=ac-c^{2}$

বা, $\fn_cm by\left (a-b \right )=c\left (a-c \right )$

$\therefore y=\frac{c\left ( a-c \right )}{b\left ( a-b \right )}$

y এর মান (i) নং সমীকরণে পাই,

$ax+b\times \frac{c\left ( a-c \right )}{b\left ( a-b \right )}=c$

বা, $ax=c-\frac{c\left ( a-c \right )}{\left ( a-b \right )}$

বা, $ax=\frac{ac-bc-ac+c^{2}}{\left ( a-b \right )}$

বা, $ax=\frac{c^{2}-ac}{a-b}$

$\therefore x=\frac{c\left ( c-a \right )}{a\left ( a-b \right )}$

নির্ণেয় সমীকরণের সমাধান ${\color{DarkGreen} x=\frac{c\left ( c-a \right )}{a\left ( a-b \right )}$ ও ${\color{DarkGreen} y=\frac{c\left ( a-c \right )}{b\left ( a-b \right )}}$

Koshe dekhi 5.3 class 9

রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) : Koshe dekhi - 5.3

4. নীচের দুইচলবিশিষ্ট সমীকরণগুলি অপনয়ন পদ্ধতিতে সমাধান করি।

(xv) $\fn_cm {\color{Blue} ax+by=1}$

$\fn_cm {\color{Blue} bx+ay=\frac{\left ( a+b \right )^{2}}{a^{2}+b^{2}}-1}$

সমাধানঃ

$ax+by=1$ ……(i)

$\fn_cm bx+ay=\frac{\left ( a+b \right )^{2}}{a^{2}+b^{2}}-1$

বা, $\fn_cm bx+ay=\frac{\left ( a+b \right )^{2}-\left (a^{2}+b^{2} \right )}{a^{2}+b^{2}}$

বা, $\fn_cm bx+ay=\frac{a^{2}+b^{2}+2ab-a^{2}-b^{2}}{a^{2}+b^{2}}$

বা, $\fn_cm bx+ay=\frac{2ab}{a^{2}+b^{2}}$ ……..(ii)

(i) নং সমীকরণকে b দ্বারা এবং (ii) নং সমীকরণকে a দ্বারা গুন্ করে পাই,

$abx+b^{2}y=b$ …….(iii)

$\fn_cm abx+a^{2}y=\frac{2a^{2}b}{a^{2}+b^{2}}$ …… (iv)

(iii) নং সমীকরণ থেকে (iv) নং সমীকরণ বিয়োগ করে পাই ,

$\fn_cm abx+b^{2}y-abx-a^{2}y=b-\frac{2a^{2}b}{a^{2}+b^{2}}$

বা, $\fn_cm b^{2}y-a^{2}y=\frac{a^{2}b+b^{3}-2a^{2}b}{a^{2}+b^{2}}$

বা, $\fn_cm \left (b^{2}-a^{2} \right )y=\frac{b\left ( b^{2}-a^{2} \right )}{a^{2}+b^{2}}$

$\fn_cm \therefore y=\frac{b}{a^{2}+b^{2}}$

y এর মান (i) নং সমীকরণে বসিয়ে পাই,

$ax+b\times \frac{b}{a^{2}+b^{2}}=1$

বা, $ax=1-\frac{b^{2}}{a^{2}+b^{2}}$

বা, $ax=\frac{a^{2}+b^{2}-b^{2}}{a^{2}+b^{2}}$

বা, $ax=\frac{a^{2}}{a^{2}+b^{2}}$

$\therefore x=\frac{a}{a^{2}+b^{2}}$

নির্ণেয় সমীকরণের সমাধান ${\color{DarkGreen} x=\frac{a}{a^{2}+b^{2}}}$ ও $\fn_cm {\color{DarkGreen} y=\frac{b}{a^{2}+b^{2}}}$

Koshe dekhi 5.3 class 9

রৈখিক সহ সমীকরণ (দুই চল বিশিষ্ট) : Koshe dekhi - 5.3

4. নীচের দুইচলবিশিষ্ট সমীকরণগুলি অপনয়ন পদ্ধতিতে সমাধান করি।

(xvi) $\fn_cm {\color{Blue} \left ( 7x-y-6 \right )^{2}+\left ( 14x+2y-16 \right )^{2}=0}$

সমাধানঃ

$\fn_cm \left ( 7x-y-6 \right )^{2}+\left ( 14x+2y-16 \right )^{2}=0$

দুটি রাশির বর্গের সমষ্টি শূন্য হলে তারা প্রত্যেকে পৃথক পৃথক ভাবে শূন্য হয়।

অর্থাৎ,

$\fn_cm \left ( 7x-y-6 \right )^{2}=0$

বা, $7x-y-6=0$

বা, $7x-y=6$ …….(i)

এবং

$\fn_cm \left ( 14x+2y-16 \right )^{2}=0$

বা, $14x+2y-16=0$

বা, $14x+2y=16$ …..(ii)

(i) নং সমীকরণকে 2 দ্বারা এবং (ii) নং সমীকরণকে 1 দ্বারা গুন্ করে পাই,

14x – 2y = 12 …….(iii)

14x + 2y = 16 …… (iv)

(iii) নং সমীকরণ থেকে (iv) নং সমীকরণ বিয়োগ করে পাই ,

14x – 2y -14x – 2y = 12 – 16

বা, − 4y = − 4

বা, $y=\frac{-4}{-4}$

∴ y = 1

y এর মান (i) নং সমীকরণে বসিয়ে পাই,

7x – 1 = 6

বা, 7x = 6 + 1

বা, 7x = 7

বা, $x=\frac{7}{7}$

∴ x = 1

নির্ণেয় সমীকরণের সমাধান x = 1 ও y = 1

Koshe dekhi 5.3 class 9

Thank You

Koshe dekhi 5.3 class 9

Koshe dekhi 5.3 class 9

Koshe dekhi 5.3 class 9

Koshe dekhi 5.3 class 9

Related Post

Koshe Dekhi 20 Class 9

Koshe Dekhi 17 Class 9

Koshe Dekhi 12 Class 9

Leave a Reply Cancel reply

You missed

NIACL Assistant Recruitment 2024 Apply Online

NIACL Assistant Recruitment 2024

Railway TTE Recruitment 2024 Online Apply, Eligibility Criteria rrcb.gov.in

Madhyamik ABTA Test Papers 2024 : Life Science Page 1022