Q1. ABC ত্রিভুজের B কোণটি সমকোণ। যদি AC-কে ব্যাস করে একটি বৃত্ত অঙ্কন করি যা AB -কে D বিন্দুতে ছেদ করে, তবে নীচের তথ্যগুলির মধ্যে কোনটি ঠিক লিখি-

(i) AB > AD (ii) AB = AD (iii) AB < AD

উত্তর : (ii) AB = AD

ব্যাখ্যা :

ΔABC -এর তিনটি বিন্দু অসমরেখ বিন্দু এবং A ও C বিন্দুটি বৃত্তের উপর অবস্থিত, তাই B বিন্দুটিও বৃত্তের উপরেই অবস্থিত হবে। (Note : তিনটি অসমরেখ বিন্দু দিয়ে কেবলমাত্র একটিই বৃত্ত অঙ্কন করা যাবে।)

প্রশ্নানুযায়ী, AB রেখাকে বৃত্তটি D বিন্দুতে ছেদ করেছে।

সুতরাং, B ও D বিন্দু দুটি একই বিন্দু হবে।

অর্থ্যাৎ, AB = AD হবে। [উঃ (ii)]

Q2. প্রমাণ করি যে, একটি সমদ্বিবাহু ত্রিভুজের সমান বাহু দুটির যে-কোনোটিকে ব্যাস করে অঙ্কিত বৃত্ত অসমান বাহুটিকে সমদ্বিখণ্ডিত করে।

সমাধানঃ 

ধরা যাক, সমদ্বিবাহু ΔABC -এর AB = AC; AB বাহুকে ব্যাস করে একটি বৃত্ত অঙ্কন করা হলো যা ত্রিভুজটির অসমান বাহু অর্থ্যাৎ, BC কে D বিন্দুতে ছেদ করেছে।

প্রমাণ করতে হবে যে, D, BC -এর মধ্যবিন্দু।

অঙ্কনঃ A, D যুক্ত করা হলো।

প্রমাণঃ যেহেতু, AB হলো বৃত্তের ব্যাস এবং D বিন্দুটি বৃত্তের উপর অবস্থিত (যেখানে, A, B, ও D অসমরেখ বিন্দু)

∴ ∠ADB = 90° (অর্ধবৃত্তস্থ কোণ)

সুতরাং, ∠ADC = 90° (∴ ∠BDC = 180°)

এখন, যেহেতু, ΔABD ও ΔADC -এর
AB = AC (স্বীকারনুযায়ী)
∠ADB = অন্তর্ভুত ∠ADC (প্রতিটি কোণের মান 90°)
এবং, AD হলো সাধারণ বাহু।

∴ ΔABD ≅ ΔADC (সর্বসমতার S-A-S সূত্রানুযায়ী)

∴ BD = CD  (অনুরূপ বাহু)

অর্থ্যাৎ, D, BC -এর মধ্যবিন্দু (প্রমাণিত)

Q3. সাহানা দুটি বৃত্ত এঁকেছে যারা পরস্পরকে P ও Q বিন্দুতে ছেদ করেছে। PA ও PB যথাক্রমে দুটি বৃত্তের ব্যাস হলে, প্রমাণ করি যে A, Q ও B বিন্দুত্রয় সমরেখ।

সমাধানঃ

ধরা যাক, M ও N কেন্দ্রীয় বৃত্ত দুটি পরস্পরকে P ও Q বিন্দুতে ছেদ করে এবং PA ও PB হলো যথাক্রমে তাদের ব্যাস। A, Q ও B, Q যুক্ত করা হলো।

প্রমাণ করতে হবে যে, A, Q, ও B বিন্দু তিনটি হলো সমরেখ বিন্দু।

অঙ্কনঃ P, Q যুক্ত করা হলো।

প্রমাণঃ যেহেতু, M কেন্দ্রীয় বৃত্তের PA হলো ব্যাস এবং Q বৃত্তের উপর অবস্থিত একটি বিন্দু। (যেখানে, P, A, ও Q বিন্দু তিনটি অসমরেখ বিন্দু)

∴ ∠PQA = 90°

একইভাবে,
যেহেতু, N কেন্দ্রীয় বৃত্তের PB হলো ব্যাস এবং Q বৃত্তের উপর অবস্থিত একটি বিন্দু। (যেখানে, P, B, ও Q বিন্দু তিনটি অসমরেখ বিন্দু)

∴ ∠PQB = 90°

এখন, ∠PQA + ∠PQB = 90° + 90° = 180° বা, 1 সরলকোণ।

যেহেতু, একই সরলরেখা PQ -এর বিপরীত দিকে যে দুটি কোণ (অর্থ্যাৎ, ∠PQA ও ∠PQB) উৎপন্ন হয়েছে তাদের সমষ্টি 180° বা, 1 সরলকোণ।

∴ AQB একটি সরলরেখা অর্থ্যাৎ, A, Q, ও B বিন্দু তিনটি হলো সমরেখ বিন্দু। (প্রমাণিত)

Q4. রজত একটি সরলরেখাংশ PQ অঙ্কন করেছে যার মধ্যবিন্দু R এবং সে PR ও PQ -কে ব্যাস করে দুটি বৃত্ত অঙ্কন করেছে। আমি P বিন্দুগামী একটি সরলরেখা অঙ্কন করেছি যা প্রথম বৃত্তকে S বিন্দুতে এবং দ্বিতীয় বৃত্তকে T বিন্দুতে ছেদ করেছে। যুক্তি দিয়ে প্রমাণ করি যে, PS = ST.

সমাধানঃ

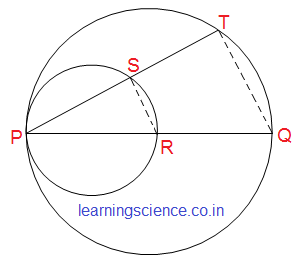ধরা যাক, PQ সরলরেখার মধ্যবিন্দু R অর্থ্যাৎ, PR = RQ; PR ও PQ কে ব্যাস করে দুটি বৃত্ত অঙ্কণ করা হলো। P বিন্দু থেকে একটি সরলরেখা অঙ্কণ করা হলো যা ছোট বৃত্তটিকে S বিন্দুতে এবং বড়ো বৃত্তটিকে T বিন্দুতে ছেদ করেছে।

প্রমাণ করতে হবে যে, PS = ST

অঙ্কনঃ R, S ও Q, T যুক্ত করা হলো।

প্রমাণঃ ∵ PR হলো ছোট বৃত্তটির ব্যাস এবং R বৃত্তের উপর অবস্থিত একটি বিন্দু। (যেখানে, P, S, ও R বিন্দু তিনটি অসমরেখ বিন্দু)

∴ ∠PSR = 90° অর্থ্যাৎ, RS ⊥ PT

একইভাবে,
∵ PQ হলো বড়ো বৃত্তের ব্যাস এবং T বৃত্তের উপর অবস্থিত একটি বিন্দু। (যেখানে, P, T, ও Q বিন্দু তিনটি অসমরেখ বিন্দু)

∴ ∠PTQ = 90° অর্থ্যাৎ, QT ⊥ PT

এখন, ∵ RS, QT ⊥ PT

∴ SR ∥ TQ

আবার, ∵

ΔPQT -এর  SR ∥ TQ

    (থ্যালেসের উপপাদ্য থেকে পাই)

বা,     [∵ PR = RQ]

বা,

(প্রমাণিত)

Q5. একটি বৃত্তের উপর তিনটি বিন্দু P, Q ও R অবস্থিত। PQ ও PR -এর উপর P বিন্দুতে অঙ্কিত লম্ব দুটি বৃত্তকে যথাক্রমে S ও T বিন্দুতে ছেদ করেছে। প্রমাণ করি যে, RQ = ST.

সমাধানঃ

ধরা যাক, P, Q  ও  R বিন্দু তিনটি একটি বৃত্তের উপর অবস্থিত। P বিন্দু থেকে PQ ও PR -এর উপর যথাক্রমে PS ও PT লম্ব অঙ্কণ করা হলো যারা বৃত্তটিকে যথাক্রমে S  ও  T বিন্দুতে ছেদ করে। S, T  ও  R, Q যুক্ত করা হলো।

প্রমাণ করতে হবে যে, RQ = ST

অঙ্কনঃ S, Q  ও  R, T যুক্ত করা হলো।

প্রমাণঃ ∵ ΔPSQ -এর ∠SPQ = 90° (অর্ধবৃত্তস্থ কোণ)
∴ SQ হলো বৃত্তটির একটি ব্যাস।

একইভাবে,
∵ ΔPTR -এর ∠TPR = 90° (অর্ধবৃত্তস্থ কোণ)
∴ TR  হলো বৃত্তটির একটি ব্যাস।

এখন, ∵ SQ  ও  TR ব্যাস দুটি পরস্পরকে  O  বিন্দুতে ছেদ করে।
∴ O বিন্দুটি বৃত্তের কেন্দ্র হবে।

∴ আমরা বলতে পারি,
OT = OR = OS = OQ = O কেন্দ্রীয় বৃত্তের ব্যাসার্ধ …(i)

এখন, ∵ ΔROQ  ও  ΔSOT -এর
OR = OT   [(i) নং সিদ্ধান্ত অনুযায়ী]
∠ROQ = অন্তর্ভুত ∠SOT (বিপ্রতীপ কোণ)
এবং, OQ = OS [(i) নং সিদ্ধান্ত অনুযায়ী]

∴ ΔROQ ≅ ΔSOT (সর্বসমতার S-A-S সূত্রানুযায়ী)

∴ RQ = ST (অনুরূপ বাহু) (প্রমাণিত)

Q6. ABC একটি সূক্ষ্মকোণী ত্রিভুজ ABC ত্রিভুজের পরিবৃত্তের ব্যাস AP; BE ও CF যথাক্রমে AC ও AB বাহুর উপর লম্ব এবং তারা পরস্পরকে Q বিন্দুতে ছেদ করে। প্রমাণ করি যে, BPCQ একটি সামান্তরিক।

সমাধানঃ

ধরা যাক, ABC একটি সূক্ষকোণী ত্রিভুজ যার পরিবৃত্তের ব্যাস হলো AP; BE ও CF হলো যথাক্রমে AC ও AB বাহুর উপর লম্ব যারা পরস্পরকে Q বিন্দুতে ছেদ করেছে। B, P ও P, C যুক্ত করা হলো।

প্রমাণ করতে হবে যে, BPCQ একটি সামান্তরিক।

প্রমাণঃ ∵ AP হলো বৃত্তের ব্যাস এবং B বিন্দুটি বৃত্তের উপর অবস্থিত (যেখানে, A, B, ও P অসমরেখ বিন্দু)
∠ABP = 90° (অর্ধবৃত্তস্থ কোণ) অর্থ্যাৎ, PB ⊥ AB

আবার, CF ⊥ AB (স্বীকারনুযায়ী)

এখন, ∵ CF ও PB উভয়ই AB -এর উপর লম্ব।
∴ CF ∥ PB অর্থ্যাৎ, CQ ∥ PB

আবার, ∵ AP হলো বৃত্তের ব্যাস এবং C বিন্দুটি বৃত্তের উপর অবস্থিত (যেখানে, A, C, ও P অসমরেখ বিন্দু)
∠ACP = 90° (অর্ধবৃত্তস্থ কোণ) অর্থ্যাৎ, PC ⊥ AC

আবার, BE ⊥ AC (স্বীকারনুযায়ী)

এখন, ∵ PC ও BE উভয়ই AC -এর উপর লম্ব।
∴ BE ∥ PC অর্থ্যাৎ, BQ ∥ PC

এখন, ∵ চতুর্ভুজ BPCQ -এর
BQ ∥ PC এবং CQ ∥ PB

∴ চতুর্ভুজ BPCQ হলো একটি সামন্তরিক। (প্রমাণিত)

Q7. একটি ত্রিভুজের শীর্ষকোণের অন্তসমদ্বিখণ্ডক ও বহির্সমদ্বিখণ্ডক ত্রিভুজটির পরিবৃত্তকে যথাক্রমে P ও Q বিন্দুতে ছেদ করে। প্রমাণ করি যে, PQ বৃত্তের একটি ব্যাস।

সমাধানঃ

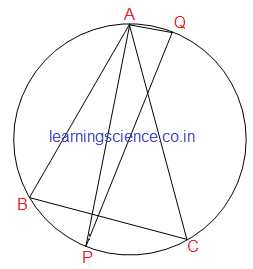ধরা যাক, ABC একটি ত্রিভুজ। ∠BAC -এর অন্তঃসমদ্বিখণ্ডক ও বহিঃসমদ্বিখণ্ডক হলো যথাক্রমে AP ও AQ, যারা ABC ত্রিভুজটির পরিবৃত্তকে যথাক্রমে P ও Q বিন্দুতে ছেদ করেছে।

প্রমাণ করতে হবে যে, PQ হলো বৃত্তের একটি ব্যাস।

প্রমাণঃ ∵ আমরা জানি, কোনো কোণের অন্তঃসমদ্বিখণ্ডক ও বহিঃসমদ্বিখণ্ডক দুটির মধ্যবর্তী কোণের মান 90°
∴ ∠PAQ = 90°

আবার, ∵ ∠PAQ = 90° এবং P, A, ও Q বিন্দু তিনটি হলো অসমরেখ বিন্দু যারা বৃত্তের উপরে অবস্থিত।
∴ ∠PAQ হবে অর্ধবৃত্তস্থ কোণ।

সুতরাং, ∠PAQ -এর বিপরীত বহু অর্থ্যাৎ, PQ হবে বৃত্তটির একটি ব্যাস। (প্রমাণিত)

Q8. AB এবং CD একটি বৃত্তের দুটি ব্যাস। প্রমাণ করি যে, ACBD একটি আয়তাকার চিত্র।

সমাধানঃ

ধরা যাক, AB ও CD একই বৃত্তের দুটি ব্যাস। A, C ; B, C ; B, D ;  ও  A, D যুক্ত করা হলো।

প্রমাণ করতে হবে যে, ACBD হলো একটি আয়তক্ষেত্র।

প্রমাণঃ ∵ AB হলো বৃত্তটির ব্যাস এবং D ও C বৃত্তের উপর অবস্থিত দুটি বিন্দু (যেখান, A, B, C ও D বিন্দুগুলি হলো অসমরেখ বিন্দু)।
∴ ∠ACB = ∠ADB = 90° (অর্ধবৃত্তস্থ কোণ)

একইভাবে,
∵ CD হলো বৃত্তটির ব্যাস এবং A ও B বৃত্তের উপর অবস্থিত দুটি বিন্দু (যেখান, A, B, C ও D বিন্দুগুলি হলো অসমরেখ বিন্দু)।
∴ ∠DAC = ∠DBC = 90° (অর্ধবৃত্তস্থ কোণ)

এখন, ∵ ACBD চতুর্ভুজের প্রতিটি কোণের মান 90° -এর সমান
অর্থ্যাৎ, ∠DAC = ∠DBC = ∠ACB = ∠ADB = 90°

∴ চতুর্ভুজ ACBD হবে একটি আয়তক্ষেত্র। (প্রমাণিত)

Q9. প্রমাণ করি, একটি রম্বসের বাহুগুলিকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তগুলি একটি নির্দিষ্ট বিন্দু দিয়ে যায়।

সমাধানঃ

ধরা যাক, ABCD রম্বসের AB , BC , CD ও DA বাহুকে ব্যাস করে চারটি বৃত্ত অঙ্কন করা হয়েছে।

প্রমাণ করতে হবে যে, ACBD রম্বসের বাহুগুলিকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তগুলি একটি নির্দিষ্ট বিন্দু দিয়ে যাবে।

অঙ্কনঃ AC ও BD কর্ণ দুটি অঙ্কন করা হলো যারা পরস্পরকে P বিন্দুতে ছেদ করে।

প্রমাণঃ ∵ কোনো রম্বসের কর্ণ দুটি পরস্পরকে সমকোণে সমদ্বিখন্ডিত করে।
∴ ∠APB = ∠BPC = ∠CPD = ∠DPA = 90°

আবার, যেহেতু আমরা জানি, অর্ধবৃত্তস্থ কোণ সমকোণ এবং অর্ধবৃত্তস্থ কোণের বিপরীত বহু ওই বৃত্তটির ব্যাস হয়। তাই, ABCD রম্বসের AB, BC, CD ও DA বাহুকে ব্যাস করে বৃত্ত অঙ্কন করলে তারা অবশ্যই একটি নির্দিষ্ট বিন্দু P দিয়ে যাবে। এক্ষেত্রে রম্বসের কর্ণদ্বয়ের ছেদবিন্দুতে যে চারটি সমকোণ উৎপন্ন হয়েছে তারা ওই বৃত্তগুলির ক্ষেত্রে অর্ধবৃত্তস্থ কোণ হবে।

সুতরাং, ACBD রম্বসের বাহুগুলিকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তগুলি একটি নির্দিষ্ট বিন্দু দিয়েই যাবে।  (প্রমাণিত)

Q10. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)

(A) বহু বিকল্পীয় প্রশ্ন (M.C.Q.) :

(i) O কেন্দ্রীয় বৃত্তে PQ একটি ব্যাস এবং PR = RQ; ∠RPQ -এর মান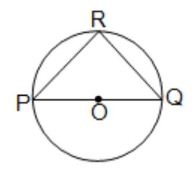

(a) 30°

(b) 90°

(c) 60°

(d) 45°

উত্তরঃ (d) 45°

ব্যাখ্যা : 

Q10. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)

(A) বহু বিকল্পীয় প্রশ্ন (M.C.Q.) :

(ii) QR বৃত্তের একটি জ্যা এবং POR বৃত্তের একটি ব্যাস। OD, QR বাহুর উপর লম্ব। OD = 4 সেমি. হলে, PQ -এর দৈর্ঘ্য

(a) 4 সেমি.

(b) 2 সেমি.

(c) 8 সেমি.

(d) কোনটিই নয়। 

উত্তরঃ (c) 8 সেমি.

ব্যাখ্যা : 

Q10. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)

(A) বহু বিকল্পীয় প্রশ্ন (M.C.Q.) :

(iii) AOB বৃত্তের ব্যাস। AC এবং BD জ্যা দুটি বর্ধিত করলে E বিন্দুতে মিলিত হয়। ∠COD = 40°  হলে, ∠CED -এর মান

(a) 40°

(b) 80°

(c) 20

(d) 70°

উত্তরঃ (d) 70°

ব্যাখ্যা : 

Q10. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)

(A) বহু বিকল্পীয় প্রশ্ন (M.C.Q.) :

(iv) AOB বৃত্তের ব্যাস। AC = 3 সেমি. ও BC = 4 সেমি. হলে, AB -এর দৈর্ঘ্য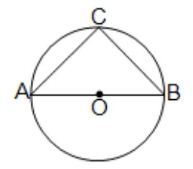

(a) 3 সেমি.

(b) 4 সেমি.

(c) 5 সেমি.

(d) 8 সেমি.

উত্তরঃ (c) 5 সেমি.

ব্যাখ্যা :

Q10. অতি সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.)

(A) বহু বিকল্পীয় প্রশ্ন (M.C.Q.) :

(v) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB ব্যাস।  BCE = 20°, CAE =2 5°  হলে , AEC -এর মান নির্ণয় করি

(a) 50°

(b) 90°

(c) 45°

(d) 20°

উত্তরঃ (c) 45°

ব্যাখ্যা :

Q10. (B) সত্য বা মিথ্যা লিখি :

(i) অর্ধবৃত্ত অপেক্ষা বৃহত্তর বৃত্তাংশস্থ কোণ স্থূলকোণ।

উত্তর : বিবৃতিটি মিথ্যা।

ব্যাখ্যা : অর্ধবৃত্ত অপেক্ষা ক্ষুদ্রতর বৃত্তাংশস্থ কোণ স্থূলকোণ।

Q10. (B) সত্য বা মিথ্যা লিখি :

(ii) ABC ত্রিভুজের AB বাহুর মধ্যবিন্দু O এবং OA = OB = OC; AB বাহুকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তটি C বিন্দু দিয়ে যাবে।

উত্তর : বিবৃতিটি সত্য।

ব্যাখ্যা : AB হলো বৃত্তের ব্যাস এবং O হলো AB -এর মধ্যবিন্দু অর্থ্যাৎ, বৃত্তের কেন্দ্র এবং যেহেতু, OA = OB = OC

সুতরাং, A, B ও C বিন্দুগুলি হয় অসমরেখ না হয় C বিন্দুটি A অথবা B বিন্দুর সাথে সমাপতিত হবে।

আবার, যেহেতু আমরা জানি, “তিনটি অসমরেখ বিন্দু দিয়ে কেবলমাত্র একটি বৃত্ত অঙ্কন করা যায়”, তাই বৃত্তটি অবশ্যই C বিন্দু দিয়ে যাবে।

Q10. (C) শূন্যস্থান পূরণ করি :

(i) অর্ধবৃত্তস্থ কোণ _______।

উত্তর : অর্ধবৃত্তস্থ কোণ সমকোণ ।

Q10. (C) শূন্যস্থান পূরণ করি :

(ii) অর্ধবৃত্ত অপেক্ষা ক্ষুদ্রতর বৃত্তাংশস্থ কোণ ______।

উত্তর : অর্ধবৃত্ত অপেক্ষা ক্ষুদ্রতর বৃত্তাংশস্থ কোণ স্থূলকোণ।

Q10. (C) শূন্যস্থান পূরণ করি :

(iii) সমকোণী ত্রিভুজের অতিভুজকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তটি ________ বিন্দু দিয়ে যাবে।

উত্তর : সমকোণী ত্রিভুজের অতিভুজকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তটি সমকৌণিক বিন্দু দিয়ে যাবে।

Q11. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)

(i) ABC সমদ্বিবাহু ত্রিভুজের AB = AC; AB বাহুকে ব্যাস করে বৃত্ত অঙ্কন করলে বৃত্তটি BC বাহুকে D বিন্দুতে ছেদ করে, BD = 4 সেমি. হলে CD -এর দৈর্ঘ্য নির্ণয় করি।

উত্তর : CD -এর দৈর্ঘ্য  4  সেমি.

ব্যাখ্যা :

Q11. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)

(ii) একটি বৃত্তে দুটি জ্যা AB এবং AC পরস্পর লম্ব AB = 4 সেমি. ও AC = 3 সেমি. হলে, বৃত্তটির ব্যাসার্ধের দৈর্ঘ্য নির্ণয় করি।

উত্তর : বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 2.5 সেমি.

ব্যাখ্যা :

Q11. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)

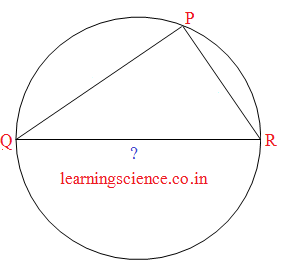
(iii) একটি বৃত্তে দুটি জ্যা PQ এবং PR পরস্পর লম্ব। বৃত্তের ব্যাসার্ধের দৈর্ঘ্য  r  সেমি. হলে, জ্যা QR -এর দৈর্ঘ্য নির্ণয় করি।

উত্তর : জ্যা QR -এর দৈর্ঘ্য  2r  সেমি.

ব্যাখ্যা :

Q11. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)

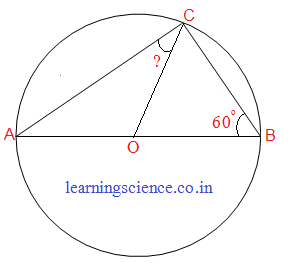
(iv) AOB বৃত্তের একটি ব্যাস। C বৃত্তের উপর একটি বিন্দু। ∠OBC = 60°  হলে  ∠OCA -এর মান নির্ণয় করি।

উত্তর : ∠OCA -এর মান  30°

ব্যাখ্যা :

Q11. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.)

(v) পাশের চিত্রে O বৃত্তের কেন্দ্র এবং AB ব্যাস। জ্যা CD -এর দৈর্ঘ্য বৃত্তের ব্যাসার্ধের দৈর্ঘ্যের সমান। AC ও BD -কে বর্ধিত করায় P বিন্দুতে ছেদ করে।  ∠APB -এর মান নির্ণয় করি।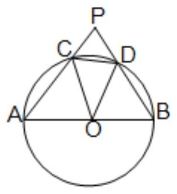

উত্তর : ∠APB -এর মান  60°

ব্যাখ্যা :