Students Request : Math (Class 5 to 10) (Part – 3)

Question 1:

ΔABC -এর পরিকেন্দ্র O এবং ∠OAB = 50° হলে, ∠ACB -এর মান হবে –

Ⓐ 50°

Ⓑ 100°

Ⓓ 80°

সমাধানঃ

∠OAB = 50°

যেহেতু, OA = OB = বৃত্তের ব্যাসার্ধ

∴ ∠OAB = ∠OBA = 50°

Δ OAB এর

∠OAB + ∠OBA + ∠AOB = 180°

বা, 50° + 50° + ∠AOB = 180°

বা, ∠AOB = 180° -100°

∴ ∠AOB = 80°

আমরা জানি, একই বৃত্তচাপের (BCA) উপর অবস্থিত পরিধিস্থ কোণ (∠ACB) কেন্দ্রস্থ কোণের ( ∠AOB ) অর্ধেক হয়।

∴ ∠ACB = $\therefore \angle ACB=\frac{\angle AOB}{2}=\frac{80^{\circ}}{2}=40^{\circ}$

উত্তরঃ Ⓒ 40°

Students Request : Math (Class 5 to 10) (Part – 3)

Question 2:

ABCD একটি বৃত্তস্থ সামান্তরিক হলে, ∠A এর মান কত হবে ?

সমাধানঃ

ABCD একটি বৃত্তস্থ সামান্তরিক হলে, ∠A এর মান 90° হবে।

কারণ, বৃত্তস্থ সামান্তরিক সর্বদা একটি আয়তক্ষেত্র হয় এবং আয়তক্ষেত্রের প্রত্যেকটি কোণের মান সর্বদা 90° হয়। (উত্তর)

Students Request : Math (Class 5 to 10) (Part – 3)

Question 3:

বছরের প্রথমে বুলু ও তুলি যথাক্রমে 36000 ও 45000 টাকা দিয়ে ব্যবসা শুরু করে। 5 মাস পরে টুসি 60000 টাকা মূলধন দেয়। যদি বছরের শেষে 40832 টাকা লাভ হয়, তাহলে কে কত টাকা পাবে ?

সমাধান :

যেহেতু 5 মাস পর টুসি 60000 টাকা মূলধন দেন, তাই 5 মাসের পর থেকে বাকি (12 − 5) মাস অর্থাৎ, 7 মাস টুসির মূলধন ব্যবসায় খাটে।

বছরের শেষে যে লভ্যাংশের পরিমাণ হবে, তা যদি টুসি প্রত্যেক মাসে পেতে চায় তবে টুসিকে প্রতিমাসে ব্যবসায় মূলধন নিয়োগ করতে হবে

= (60000 × 7)

= 420000 টাকা

যেহেতু, বুলু ও তুলি বছরের মাঝে কোনো মূলধন নিয়োগ করেনি বা তুলে নেয়নি, তাই বুলু ও তুলির মূলধনের পরিমাণ হবে যথাক্রমে 36000 ও 45000 টাকা।

বছরের শেষে যে লভ্যাংশের পরিমাণ হবে, তা যদি বুলু প্রত্যেক মাসে পেতে চায় তবে বুলুকে প্রতিমাসে ব্যবসায় মূলধন নিয়োগ করতে হবে

= (36000 × 12)

= 432000 টাকা

আবার, বছরের শেষে যে লভ্যাংশের পরিমাণ হবে, তা যদি তুলি প্রত্যেক মাসে পেতে চায় তবে তুলিকে প্রতিমাসে ব্যবসায় মূলধন নিয়োগ করতে হবে

= (45000 × 12)

= 540000 টাকা

বুলু , তুলি ও টুসির মূলধনের অনুপাত

= 432000 : 540000 : 420000

= 432 : 540 : 420

= 144 : 180 : 140

= 72 : 90 : 70

= 36 : 45 : 35

এখন,

বুলুর মূলধনের অনুপাতিক ভাগহার

$=\frac{36}{36+45+35}$

$=\frac{36}{116}$

তুলির মূলধনের অনুপাতিক ভাগহার

$=\frac{45}{36+45+35}$

$=\frac{45}{116}$

এবং টুসির মূলধনের অনুপাতিক ভাগহার

$=\frac{35}{36+45+35}$

$=\frac{35}{116}$

মোট লভ্যাংশের পরিমাণ = 40832 টাকা

সুতরাং, 40832 টাকা থেকে

বুলুর লভ্যাংশ হবে

$=40832\times \frac{36}{116}$

= 12672 টাকা।

তুলির লভ্যাংশ হবে

$=40832\times \frac{45}{116}$

= 15840 টাকা।

এবং টুসির লভ্যাংশ হবে

$=40832\times \frac{35}{116}$

= 12320 টাকা।

উত্তরঃ নির্ণেয় লভ্যাংশ থেকে বুলু পাবে 12672 টাকা, তুলি পাবে 15840 টাকাএবং টুসি পাবে 12320 টাকা।

Students Request : Math (Class 5 to 10) (Part – 3)

Question 4:

একটি লম্ববৃত্তাকার চোঙের আয়তন এবং বক্রতলের ক্ষেত্রফল সাংখ্যমানে সমান হলে উহার ব্যাসার্ধ নির্ণয় কর।

সমাধান :

Students Request : Math (Class 5 to 10) (Part – 3)

Question 5:

O কেন্দ্রীয় বৃত্তের AC ব্যাস, ABC বৃত্তস্থ ত্রিভুজ এবং OP ⊥ AB । প্রমাণ করো যে, OP : BC = 1 : 2

সমাধান :

Students Request : Math (Class 5 to 10) (Part – 3)

Question 6:

কোন বৃত্তের ${\color{Blue} 5\sqrt{2}}$ সেমি. দৈর্ঘ্যের একটি জ্যা ওই বৃত্তের কেন্দ্রে সমকোণ উৎপন্ন করে। বৃত্তের ব্যাসের দৈর্ঘ্য কত ?

সমাধান :

Students Request : Math (Class 5 to 10) (Part – 3)

Question 7:

যদি ${\color{Blue} x+y+z=1,xy+yz+zx=2}$ এবং ${\color{Blue} xyz=-3}$ হয়, তবে প্রমান করো যে ${\color{Blue} \frac{1}{x+yz}}+{\color{Blue} \frac{1}{y+zx}}+{\color{Blue} \frac{1}{z+xy}=2}$

সমাধান :

Something Wrong in Question.

Students Request : Math (Class 5 to 10) (Part – 3)

Question 8:

লোহার পাতে তৈরি একটি গোলকের ব্যাস 14 সেমি.। গোলকটির রং করতে প্রতি বর্গ সেমি 2.50 টাকা হিসাবে কত খরচ পড়বে হিসাব করি।

সমাধান :

প্রদত্ত, গোলকের ব্যাস (2r) = 14 সেমি.

∴ গোলকের ব্যাসার্ধ (r) = $\frac{14}{2}$ সেমি.

∴ r = 7 সেমি.

এখন, গোলকটির বক্রতল বা সমগ্রতলের ক্ষেত্রফল (A),

$=4\pi r^{2}$

r –এর মান বসিয়ে পাই,

$=4\times \frac{22}{7}\times \left ( 7 \right )^{2}$ ${\color{Blue} \left [ \pi =\frac{22}{7} \right ]}$ বর্গ সেমি.

$=4\times \frac{22}{7}\times 7\times 7$ বর্গ সেমি.

$=4\times 22\times 7$ বর্গ সেমি.

$=616$ বর্গ সেমি.

এখন, গোলকটির পৃষ্ঠতল প্রতি বর্গ সেমি. 2.50 টাকা হিসাবে রং করতে মোট খরচ পড়বে,

= 616 × 2.50 টাকা

= 1540 টাকা

উত্তরঃ নির্ণেয় মোট খরচের পরিমান 1540 টাকা।

Students Request : Math (Class 5 to 10) (Part – 3)

Question 9:

একই দৈর্ঘ্যের ভূমিতলের ব্যাসার্ধ এবং একই উচ্চতাবিশিষ্ট একটি নিরেট শব্ঙ্কু ও একটি নিরেট লম্ববৃত্তাকার চোঙের বক্রতলের ক্ষেত্রফলের অনুপাত 5 : 8 হলে, উহাদের ভূমির ব্যাসার্ধের দৈর্ঘ্য ও উচ্চতার অনুপাত নির্ণয় করি।

সমাধান :

উত্তরঃ নির্ণেয় ভূমির ব্যাসার্ধ এবং উচ্চতার অনুপাত 3 : 4।

Students Request : Math (Class 5 to 10) (Part – 3)

Question 10: ${\color{Blue} \frac{x^{2}+y^{2}}{2xy}}$ -এর মান লিখি যখন ${\color{Blue} x+y=9,\, x-y=5}$

সমাধান :

$x^{2}+y^{2}$

$=\frac{1}{2}\left [ \left ( x+y \right )^{2} +\left ( x-y \right )^{2}\right ]$

$=\frac{1}{2}\left [ \left ( 9 \right )^{2} +\left ( 5 \right )^{2}\right ]$

$=\frac{1}{2}\left ( 81+25 \right )$

$=\frac{1}{2}\times 126$

$=63$

আবার,

$2xy$

$=\frac{1}{2}\times 4xy$

$=\frac{1}{2}\left [ \left ( x+y \right )^{2}-\left ( x-y \right )^{2} \right ]$

$=\frac{1}{2}\left [ \left ( 9 \right )^{2} -\left ( 5 \right )^{2}\right ]$

$=\frac{1}{2}\left ( 81-25 \right )$

$=\frac{1}{2}\times 56$

$=28$

এখন,

$\frac{x^{2}+y^{2}}{2xy}$

$=\frac{63}{28}$

$=\frac{9}{4}$

$=2\frac{1}{4}$ (উত্তর)

Students Request : Math (Class 5 to 10) (Part – 3)

Question 11: একটি লম্ববৃত্তাকার শঙ্কুর তির্যক উচ্চতা 7 সেমি ও সমগ্রতলের ক্ষেত্রফল 147.84 বর্গ সেমি হলে শঙ্কুর ভূমির ব্যাসার্ধ কত হবে?

সমাধান :

উত্তরঃ নির্ণেয় ব্যাসার্ধের দৈর্ঘ্য 4.2 সেমি.।

Students Request : Math (Class 5 to 10) (Part – 3)

Question 12: ${\color{Blue} 3x-4y\propto \sqrt{xy}}$ হলে, প্রমাণ করা যে ${\color{Blue} x^{2}+y^{2}\propto xy}$

সমাধান :

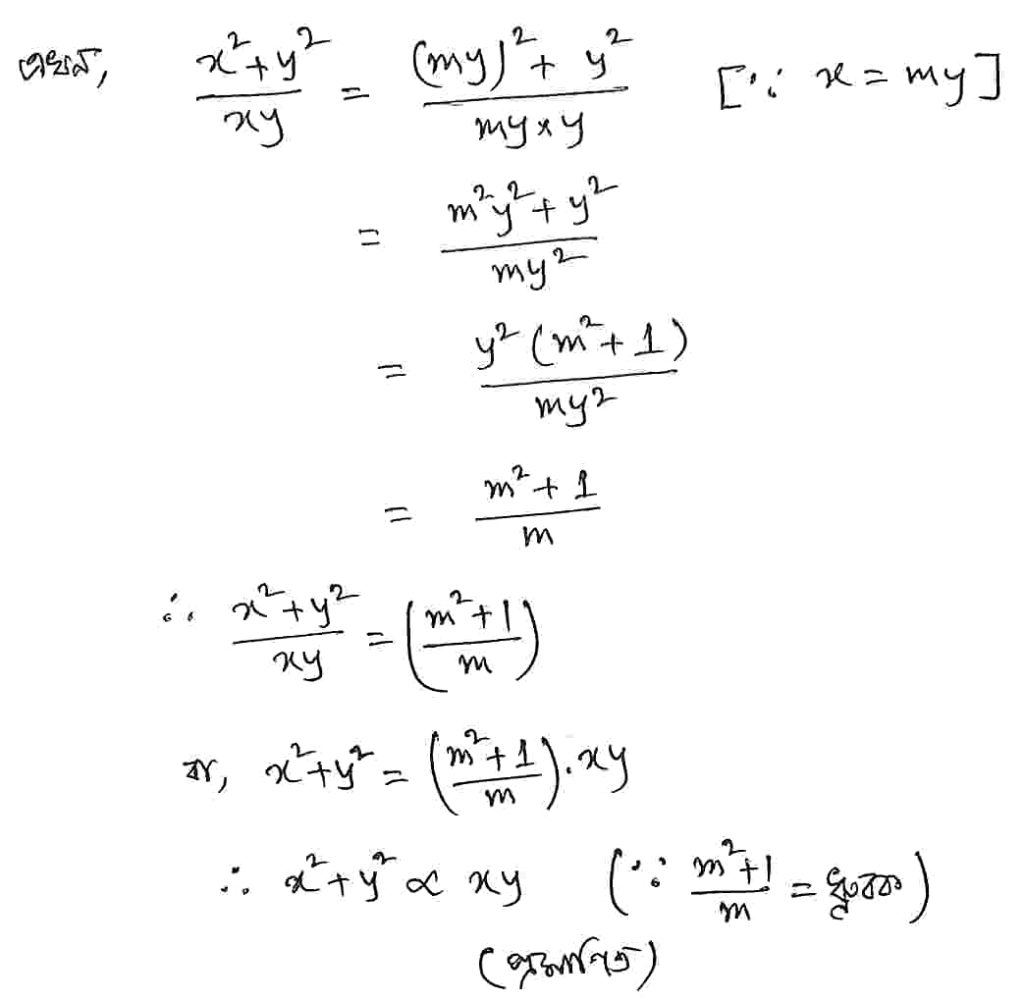
Students Request : Math (Class 5 to 10) (Part – 3)

Question 13: 4 জন পুরুষ , 6 জন স্ত্রীলোক এবং7 জন বালক কে 112 টাকা এমন ভাবে ভাগ করে দাও যেন প্রত্যেক পুরুষ , প্রত্যেক বালকের 3 গুণ ও প্রত্যেক স্ত্রী লোকের দ্বিগুণ পায়৷

সমাধান :

পুরুষ = M

স্ত্রীলোক = F

বালক = B

প্রশ্নানুযায়ী,

$\frac{M}{B}=\frac{3}{1}$ এবং $\frac{M}{F}=\frac{2}{1}$

এখন,

$\frac{M}{B}=\frac{3\times 2}{1\times 2}=\frac{6}{2}$ এবং

$\frac{M}{F}=\frac{2\times 3}{1\times 3}=\frac{6}{3}$

সুতরাং, $M:F:B=6:3:2$

অর্থ্যাৎ, $4M:6F:7B$

$=4\times 6:6\times 3:7\times 2$

$=24:18:14$

$=12:9:7$

আনুপাতিক সমষ্টি = 12 + 9 + 7 = 28

112 টাকার মধ্যে 4 জন পুরুষ মোট ভাগ পাবে,

$=112\times \frac{12}{28}$ টাকা

$=4\times 12$ টাকা

$=48$ টাকা (উত্তর)

112 টাকার মধ্যে 6 জন স্ত্রীলোক মোট ভাগ পাবে,

$=112\times \frac{9}{28}$ টাকা

$=4\times 9$ টাকা

$=36$ টাকা (উত্তর)

112 টাকার মধ্যে 7 জন বালক মোট ভাগ পাবে,

$=112\times \frac{7}{28}$ টাকা

$=4\times 7$ টাকা

$=28$ টাকা (উত্তর)

Students Request : Math (Class 5 to 10) (Part – 3)

Question 14: (3x − 2y) : (x + 3y) = 5 : 6 হলে, (2x − 5y) : (3x + 4y) নির্ণয় করি।

সমাধান :

উত্তরঃ

Students Request : Math (Class 5 to 10) (Part – 3)

Question 15: a : b = c : d হলে দেখাই যে ${\color{Blue} \left ( a^{2}+c^{2} \right )\left ( b^{2}+d^{2} \right )=\left ( ab+cd \right )^{2}}$

সমাধান :

a : b = c : d

বা, $\frac{a}{b}=\frac{c}{d}$

বা, $\frac{a}{b}=\frac{c}{d}=k$ (ধরি)

∴ a = bk ও c = dk

বামপক্ষ :

$\left ( a^{2}+c^{2} \right )\left ( b^{2}+d^{2} \right )$

$=\left [ \left ( bk \right )^{2}+\left ( dk \right )^{2} \right ]\left ( b^{2}+d^{2} \right )$

$=\left [\left (b^{2}k^{2} \right )+\left (d^{2}k^{2} \right ) \right ]\left ( b^{2}+d^{2} \right )$

$=\left [k^{2}\left (b^{2}+d^{2} \right ) \right ]\left ( b^{2}+d^{2} \right )$

$=k^{2}\left (b^{2}+d^{2} \right )^{2}$

ডানপক্ষ :

$\left ( ab+cd \right )^{2}$

$=\left ( bk\times b+dk\times d \right )^{2}$

$=\left (b^{2}k+d^{2}k \right )^{2}$

$=\left [k\left (b^{2}+d^{2} \right ) \right ]^{2}$

$=k^{2}\left (b^{2}+d^{2} \right )^{2}$

∴ বামপক্ষ = ডানপক্ষ

${\color{DarkGreen} \therefore \left ( a^{2}+c^{2} \right )\left ( b^{2}+d^{2} \right )=\left ( ab+cd \right )^{2}}$ (প্রমাণিত)

Students Request : Math (Class 5 to 10) (Part – 3)

Question 16: x : a = y : b = z : c হলে দেখাই যে ${\color{Blue} \frac{x^{3}}{a^{3}}+\frac{y^{3}}{b^{3}}+\frac{z^{3}}{c^{3}}=\frac{3xyz}{abc}}$

সমাধান :

x : a = y : b = z : c

বা, $\frac{x}{a}=\frac{y}{b}=\frac{z}{c}$

বা, $\frac{x}{a}=\frac{y}{b}=\frac{z}{c}=k$ (ধরি)

∴ x = ak, y = bk এবং z = ck

বামপক্ষ :

$\frac{x^{3}}{a^{3}}+\frac{y^{3}}{b^{3}}+\frac{z^{3}}{c^{3}}$

$=\frac{\left ( ak \right )^{3}}{a^{3}}+\frac{\left ( bk \right )^{3}}{b^{3}}+\frac{\left ( ck \right )^{3}}{c^{3}}$

$=\frac{a^{3}k^{3}}{a^{3}}+\frac{b^{3}k^{3}}{b^{3}}+\frac{c^{3}k^{3}}{c^{3}}$

$=k^{3}+k^{3}+k^{3}$

$=3k^{3}$

ডানপক্ষ :

$\frac{3xyz}{abc}$

$=\frac{3\times ak\times bk\times ck}{abc}$

$=\frac{3abck^{3}}{abc}$

$=3k^{3}$

∴ বামপক্ষ = ডানপক্ষ

${\color{DarkGreen} \therefore \frac{x^{3}}{a^{3}}+\frac{y^{3}}{b^{3}}+\frac{z^{3}}{c^{3}}=\frac{3xyz}{abc}}$ (প্রমাণিত)

Students Request : Math (Class 5 to 10) (Part – 3)

Question 17: যদি, a : b = e : d হয় তবে প্রমাণ করো ${\color{Blue} a^{3}+b^{3}:a^{3}-b^{3}=e^{3}+d^{3}:e^{3}-d^{3}}$

সমাধান :

a : b = e : d

বা, $\frac{a}{b}=\frac{e}{d}$

বা, $\frac{a}{b}=\frac{e}{d}=k$ (ধরি)

∴ a = bk, e = dk

বামপক্ষ :

$a^{3}+b^{3}:a^{3}-b^{3}$

$=\frac{a^{3}+b^{3}}{a^{3}-b^{3}}$

$=\frac{\left ( bk \right )^{3}+b^{3}}{\left ( bk \right )^{3}-b^{3}}$

$=\frac{b^{3}k^{3}+b^{3}}{b^{3}k^{3}-b^{3}}$

$=\frac{b^{3}\left (k^{3}+1 \right )}{b^{3}\left (k^{3}-1 \right )}$

$=\frac{\left (k^{3}+1 \right )}{\left (k^{3}-1 \right )}$

ডানপক্ষ :

$e^{3}+d^{3}:e^{3}-d^{3}$

$=\frac{e^{3}+d^{3}}{e^{3}-d^{3}}$

$=\frac{\left ( dk \right )^{3}+d^{3}}{\left ( dk \right )^{3}-d^{3}}$

$=\frac{d^{3}k^{3}+d^{3}}{d^{3}k^{3}-d^{3}}$

$=\frac{d^{3}\left (k^{3}+1 \right )}{d^{3}\left (k^{3}-1 \right )}$

$=\frac{\left (k^{3}+1 \right )}{\left (k^{3}-1 \right )}$

∴ বামপক্ষ = ডানপক্ষ

${\color{DarkGreen} a^{3}+b^{3}:a^{3}-b^{3}=e^{3}+d^{3}:e^{3}-d^{3}}$ (প্রমাণিত)

Students Request : Math (Class 5 to 10) (Part – 3)

Question 18: ${\color{Blue} \frac{x}{a}=\frac{y}{2b}=\frac{z}{3c}}$ হলে, ${\color{Blue} \frac{6x+3y-2z}{12x}}$ -এর মান কত হবে ?

সমাধান :

প্রদত্ত,

$\frac{x}{a}=\frac{y}{2b}=\frac{z}{3c}$

ধরি, $\frac{x}{a}=\frac{y}{2b}=\frac{z}{3c}=k$

∴ x = ak, y = 2bk ও z = 3ck

এখন,

$\frac{6x+3y-2z}{12x}$ -এর মান

$=\frac{6\times ak+3\times 2bk-2\times 3ck}{12\times ak}$

$=\frac{6ak+6bk-6ck}{12ak}$

$=\frac{6k\left (a+b-c \right )}{12ak}$

${\color{DarkGreen} =\frac{\left (a+b-c \right )}{2a}}$ (উত্তর)

Students Request : Math (Class 5 to 10) (Part – 3)

Question 19: ${\color{Blue} \frac{x}{2}=\frac{y}{3}=\frac{z}{7}}$ হলে, ${\color{Blue} \frac{2x-3y+4z}{2y}}$ -এর মান কত হবে ?

সমাধান :

প্রদত্ত,

$\frac{x}{2}=\frac{y}{3}=\frac{z}{7}$

ধরি, $\frac{x}{2}=\frac{y}{3}=\frac{z}{7}=k$

∴ x = 2k, y = 3k ও z = 7k

এখন,

$\frac{2x-3y+4z}{2y}$ -এর মান

$=\frac{2\times 2k-3\times 3k+4\times 7k}{2\times 3k}$

$=\frac{4k-9k+28k}{6k}$

$=\frac{23k}{6k}$

${\color{DarkGreen} =\frac{23}{6}}$ (উত্তর)

Students Request : Math (Class 5 to 10) (Part – 3)

Question 20: প্রমাণ করো ${\color{Blue} \frac{1}{cosec\alpha -cot\alpha }-\frac{1}{sin\alpha }=\frac{1}{sin\alpha }-\frac{1}{cosec\alpha +cot\alpha }}$

সমাধান :

বামপক্ষ :

$\frac{1}{cosec\alpha -cot\alpha }-\frac{1}{sin\alpha }$

$=\frac{\left (cosec\alpha +cot\alpha \right ) }{\left (cosec\alpha +cot\alpha \right )\left (cosec\alpha -cot\alpha \right )}-\frac{1}{sin\alpha }$

$=\frac{\left ( cosec\alpha +cot\alpha \right )}{cosec^{2}\alpha -cot^{2}\alpha}-cosec\alpha$

$=cosec\alpha +cot\alpha -cosec\alpha \; {\color{Blue} \left [ \because cosec^{2}\alpha -co^{2}t\alpha=1 \right ]}$

$=cot\alpha$

ডানপক্ষ :

$\frac{1}{sin\alpha }-\frac{1}{cosec\alpha +cot\alpha }$

$=\frac{1}{sin\alpha }-\frac{\left (cosec\alpha -cot\alpha \right ) }{\left (cosec\alpha +cot\alpha \right )\left (cosec\alpha -cot\alpha \right )}$

$=cosec\alpha-\frac{\left ( cosec\alpha -cot\alpha \right )}{cosec^{2}\alpha -cot^{2}\alpha}$

$=cosec\alpha -cosec\alpha +cot\alpha \; {\color{Blue} \left [ \because cosec^{2}\alpha -co^{2}t\alpha=1 \right ]}$

$=cot\alpha$

∴ বামপক্ষ = ডানপক্ষ (প্রমাণিত)

Students Request : Math (Class 5 to 10) (Part – 3)

Question 21: প্রমাণ করো ${\color{Blue} \sqrt{\frac{cosec\theta -1}{cosec\theta +1}}=\frac{1-sin\theta}{cos\theta}}$

সমাধান :

বামপক্ষ :

$\sqrt{\frac{cosec\theta -1}{cosec\theta +1}}$

$=\sqrt{\frac{\left ( cosec\theta -1 \right )^{2}}{\left ( cosec\theta +1 \right )\left ( cosec\theta +1 \right )}}$

$=\sqrt{\frac{\left ( cosec\theta -1 \right )^{2}}{cosec^{2}\theta -1}}$

$=\sqrt{\frac{\left ( cosec\theta -1 \right )^{2}}{cot^{2}\theta}}\; \; {\color{Blue} \left [ \because cosec^{2}\theta -1=cot^{2}\theta \right ]}$

$=\frac{cosec\theta -1}{cot\theta}$

$=\frac{\frac{1}{sin\theta}-1}{\frac{cos\theta}{sin\theta}}$

$=\frac{\left (\frac{1-sin\theta}{sin\theta} \right )}{\frac{cos\theta}{sin\theta}}$

$=\frac{1-sin\theta}{cos\theta}$ = ডানপক্ষ (প্রমাণিত)

Students Request : Math (Class 5 to 10) (Part – 3)

Question 22: θ ধনাত্মক সূক্ষকোণ হলে secθ -এর মান হতে পারে না –

Ⓐ 1 -এর চেয়ে বেশি

Ⓑ 1 -এর চেয়ে কম

Ⓓ 0

সমাধান :

সঠিক নির্বাচনটি হবে Ⓑ 1 -এর চেয়ে কম

θ ধনাত্মক সূক্ষকোণ হলে secθ -এর মান 1 -এর চেয়ে কম হতে পারে না।

উত্তরঃ

Students Request : Math (Class 5 to 10) (Part – 3)

Question 23:

In ΔABC, DE//BC, ${\color{Blue} \frac{AD}{DB}=\frac{2}{5}}$ ; If AC = 21 cm, find AE = ?

সমাধান :

Students Request : Math (Class 5 to 10) (Part – 3)

Question 24:

${\color{Blue} 5x^{2}-11x+k=0}$ সমীকরণের বীজদ্বয় পরস্পরের অন্যোন্যক হলে, k এর মান –

(a) −5

(b) 5

(d) 11

সমাধান :

Students Request : Math (Class 5 to 10) (Part – 3)

Question 25:

${\color{Blue} ax^{2}+abcx-bc=0 \left ( a,b,c>0 \right )}$ দ্বিঘাত সমীকরণের বীজদ্বয় সমান ও বিপরীত চিহ্নযুক্ত হবে যখন –

(a) abc = 0

(b) bc = 0

(d) a + bc = 0

সমাধান :

Students Request : Math (Class 5 to 10) (Part – 3)

Question 26:

A ও B যৌথভাবে ব্যবসা শুরু করে। A-এর মূলধন B-এর মূলধনের দ্বিগুণ। 3 মাস পরে A তার মূলধনের 1/3 অংশ তুলে নেয় কিন্তু 7 মাস পরে যত অংশ তুলে নিয়েছিল তারই 1/3 অংশ জমা দেয় এবং B তার মূলধনের 1/4 অংশ তুলে নেয়। বছরের শেষে A-এর লভ্যাংশ 300 টাকা হলে B-এর লভ্যাংশ কত টাকা হবে?

সমাধান :

ধরি B- এর মূলধন = x টাকা

সুতরাং A-এর মূলধন = 2x টাকা

3 মাস পরে A মূলধন তুলে নেয়

$=\frac{2x}{3}$ টাকা

3মাস পর A-এর মূলধন হবে

$=\left ( 2x-\frac{2x}{3} \right )$ টাকা

$=\frac{4x}{3}$ টাকা

7 মাস পরে A মূলধন নিয়োগ করে

$=\frac{2x}{3}\times \frac{1}{3}$ টাকা

$=\frac{2x}{9}$ টাকা

7 মাস পর A-এর মূলধন হবে

$=\left ( \frac{4x}{3}+\frac{2x}{9} \right )$ টাকা

$=\frac{14x}{9}$ টাকা

বছরের শেষে যে লাভ হয় সেই লাভ প্রতিমাসে পেতে হলে A-কে বার্ষিক মূলধন নিয়োগ করতে হবে,

$=\left ( 2x\times 3 \right )+\left (\left ( 7-3 \right )\times \frac{4x}{3} \right )+\left (\left ( 12-7 \right )\times \frac{14x}{9} \right )$ টাকা

$=6x+\frac{16x}{3}+\frac{70x}{9}$ টাকা

$=\frac{172x}{9}$ টাকা

7 মাস পরে B মূলধন তুলে নেয়

$=\frac{x}{4}$ টাকা

7 মাস পর B-এর মূলধন হবে

$=\left ( x-\frac{x}{4} \right )$ টাকা

$=\frac{3x}{4}$ টাকা

বছরের শেষে যে লাভ হয় সেই লাভ প্রতিমাসে পেতে হলে B-কে বার্ষিক মূলধন নিয়োগ করতে হবে,

$=\left ( 7\times x \right )+\left ( \left ( 12-7 \right )\times \frac{3x}{4} \right )$ টাকা

$=\left (7x+\frac{15x}{4} \right )$ টাকা

$=\frac{43x}{4}$ টাকা

A ও B- এর মূলধনের অনুপাত

$=\frac{172x}{9}:\frac{43x}{4}$

$=\frac{172}{9}:\frac{43}{4}$

$=\left (\frac{172}{9}\times 36 \right ):\left (\frac{43}{4}\times 36 \right )$

$=688:387$

$=\left ( 688\times \frac{300}{688} \right ):\left ( 387\times \frac{300}{688} \right )$

$=300:168.75$

সুতরাং A -এর মূলধন 300 টাকা হলে B -এর মূলধন হবে 168.75 টাকা।

উত্তরঃ B -এর মূলধনের পরিমান 168.75 টাকা।

Students Request : Math (Class 5 to 10) (Part – 3)

Question 27:

10টি কামান প্রতি 5 মিনিটে 3 বার গোলা ছুড়ে ${\color{Blue} 1\frac{1}{2}}$ ঘণ্টায় 270টি টার্গেট বিদ্ধ করলে 25টি কামান প্রতি 6 মিনিটে 5 বার গোলা ছুড়ে 1 ঘন্টায় ক-টি টার্গেট বিদ্ধ করতে পারবে?

সমাধান :

ভেদ তত্ত্বের প্রয়োগের মাধ্যমে এই গাণিতিক সমস্যাটি অতি সহজে সমাধান করা যায়।

ধরি, টার্গেটের সংখ্যা x টি, কামানের সংখ্যা c টি, গোলা ছোড়ার পরিমাণ y টি/মিনিট এবং সময়ের পরিমাণ t ঘন্টা।

মিশ্র ভেদের উপপাদ্য প্রয়োগে লেখা যায়,

$x\propto cyt$

$\therefore x=kcyt$ যেখানে k = অশুণ্য ভেদ ধ্রুবক।

আমরা লিখতে পারি,

$k=\frac{x}{cyt}$

x = 270 টি , c = 10 টি, y = $\frac{3}{5}$ টি/মিনিট এবং t = $1\frac{1}{2}=\frac{3}{2}$ ঘন্টা হলে,

$k=\frac{270}{\left ( 10\times \frac{3}{5}\times \frac{3}{2} \right )}$

$\therefore k=30$

এখন, k = 30, c = 25 টি, y = $\frac{5}{6}$ টি/মিনিট এবং t = 1 ঘন্টা হলে,

$x=kcyt\Rightarrow \left ( 30\times 25\times \frac{5}{6}\times 1 \right )$

$\therefore x=625$ টি

উত্তরঃ নির্ণেয় 1 ঘন্টায় 625 টি বিদ্ধ করা যাবে।

Students Request : Math (Class 5 to 10) (Part – 3)

Question 28:

10 বছর পর স্ত্রী ও পুত্র 3 : 2 অনুপাতে ভাগ পাবে এই শর্তে এক ব্যক্তি বার্ষিক 14% সরল সুদের হারে সরকারি ঋণপত্র ক্রয় করেন। মেয়াদ শেষে তার পুত্র 6720 টাকা পেলে তিনি কত টাকার ঋণপত্র কিনেছিলেন?

সমাধান :

স্ত্রীর প্রাপ্ত অর্থ : পুত্রের প্রাপ্ত অর্থ

= 3 : 2

$=\left ( 3\times \frac{6720}{2} \right ):\left ( 2\times \frac{6720}{2} \right )$

$=10080:6720$

অর্থাৎ, পুত্রের প্রাপ্ত অর্থ = 6720 টাকা হলে

স্ত্রীর প্রাপ্ত অর্থ হবে = 10080 টাকা

∴ মোট = (6720 + 10080) টাকা (= সুদ-আসল)

ধরি ঋণপত্রের পরিমাণ P টাকা

10 বছরের সরল সুদ (I) = (16800 − P) টাকা

এখন, $I=\frac{Ptr}{100}$ সূত্র থেকে পাই,

বা, $16800-P=\frac{P\times 10\times 14}{100}\; \; {\color{Blue} \left [ t=10,r=14 \right ]}$

বা, $140P=1680000-100P$

বা, $240P=1680000$

বা, $P=\frac{1680000}{240}$

$\therefore P=7000$ টাকা

উত্তরঃ নির্ণেয় ঋণপত্রের পরিমাণ 7000 টাকা।

Students Request : Math (Class 5 to 10) (Part – 3)

Question 28:

A, B, C একটি অংশীদারি কারবার এই শর্তে শুরু করল যে লাভের 1/3 অংশ ব্যবসা বৃদ্ধির জন্য এবং বাকি টাকা 5 : 4 : 3 অনুপাতে ভাগ হবে। বছরের শেষে A, C -এর চেয়ে 500 টাকা বেশি পেলে লাভের বাৎসরিক পরিমাণ কত?

সমাধান :

Students Request : Math (Class 5 to 10) (Part – 3)

Question 28:

এক ব্যাক্তি তার সঞ্চয়ের কিছু অংশ ব্যাংকে ও বাকি অংশ পোস্ট অফিসে রাখায় তার বছরের শেষে যা আয় হয়,সমস্ত টাকা ব্যাংকে রাখলে তার 50 টাকা বেশি আয় হতো। যদি ব্যাংক ও পোস্ট অফিসে বার্ষিক সুদের হার যথক্রমে 10% ও 8% হয় তবে তিনি ব্যাংক ও পোস্ট অফিসে কত করে টাকা রেখেছিলেন। তার সঞ্চয়ের পরিমাণ 5700 টাকা।

সমাধান :

Student request