Koshe Dekhi 20 Class 10 |
koshe dekhi 20 class 10
Q1. নিমলিখিতগুলিকে ডিগ্রি, মিনিট ও সেকেন্ডে প্রকাশ করি :
(i) 832′
∵ আমরা জানি, 1° = 60′
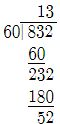
∴ 832′ = 13’52” (Answer)
koshe dekhi 20 class 10
Q1. নিমলিখিতগুলিকে ডিগ্রি, মিনিট ও সেকেন্ডে প্রকাশ করি :
(ii) 6312”
সমাধান :
∵ আমরা জানি, 1′ = 60”

∴ 6312” = 105’12”
আবার, যেহেতু 105 > 60
∴ 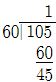 [∵ 1° = 60′]
[∵ 1° = 60′]
∴ 105′ = 1°45′
সুতরাং, 6312” = 1°45’12” (Answer)
koshe dekhi 20 class 10
Q1. নিমলিখিতগুলিকে ডিগ্রি, মিনিট ও সেকেন্ডে প্রকাশ করি :
(iii) 375”
সমাধান :
∵ আমরা জানি, 1′ = 60”
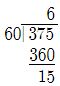
∴ 375” = 6’15” (Answer)
koshe dekhi 20 class 10
Q1. নিমলিখিতগুলিকে ডিগ্রি, মিনিট ও সেকেন্ডে প্রকাশ করি :
(iv)
সমাধান :
koshe dekhi 20 class 10
Q1. নিমলিখিতগুলিকে ডিগ্রি, মিনিট ও সেকেন্ডে প্রকাশ করি :
(v) 72.04°
সমাধান :
(Answer)
koshe dekhi 20 class 10
Q2. নিম্নলিখিতগুলির বৃত্তীয় মান নির্ণয় করি :
(i) 60°
সমাধান :
(Answer)
koshe dekhi 20 class 10
Q2. নিম্নলিখিতগুলির বৃত্তীয় মান নির্ণয় করি :
(ii) 135°
সমাধান :
(Answer)
koshe dekhi 20 class 10
Q2. নিম্নলিখিতগুলির বৃত্তীয় মান নির্ণয় করি :
(iii) −150°
সমাধান :
(Answer)
koshe dekhi 20 class 10
Q2. নিম্নলিখিতগুলির বৃত্তীয় মান নির্ণয় করি :
(iv) 72°
সমাধান :
(Answer)
koshe dekhi 20 class 10
Q2. নিম্নলিখিতগুলির বৃত্তীয় মান নির্ণয় করি :
(v) 22°30′
সমাধান :
22°30′
এখন,
∴ 22°30′ (Answer)
koshe dekhi 20 class 10
Q2. নিম্নলিখিতগুলির বৃত্তীয় মান নির্ণয় করি :
(vi) − 62°30′
সমাধান :
− 62°30′
এখন,
∴ − 62°30′ (Answer)
koshe dekhi 20 class 10
Q2. নিম্নলিখিতগুলির বৃত্তীয় মান নির্ণয় করি :
(vii) 52°52’30”
সমাধান :
এখন,
∴
(Answer)
koshe dekhi 20 class 10
Q2. নিম্নলিখিতগুলির বৃত্তীয় মান নির্ণয় করি :
(viii) 40°16’24”
সমাধান :
এখন,
∴
(Answer)
koshe dekhi 20 class 10
Q3. -এর AC = BC এবং BC বাহুকে D পর্যন্ত বর্ধিত করলাম। যদি
হয়, তবে ABC ত্রিভুজের প্রতিটি কোণের বৃত্তীয় মান নির্ণয় করি।
সমাধান :

(1 সরলকোণ)
আবার,
∴ এখন, 36° এর বৃত্তীয় মান =
এবং, 72° এর বৃত্তীয় মান =
উত্তর : ΔABC এর এবং
koshe dekhi 20 class 10
Q4. একটি সমকোণী ত্রিভুজের সূক্ষ্মকোণ দুটির অন্তর হলে, ষষ্টিক পদ্ধতিতে ওই কোণদ্বয়ের মান লিখি।
সমাধান :
∵ সমকোণী ত্রিভুজের যে কোনো একটি কোণ সমকোণ।
∴ অপর দুটি সূক্ষকোণ পরস্পর পূরক কোণ (অর্থাৎ, কোণ দুটির সমষ্টি 90° এর সমান)।
ধরি, কোণ দুটির মান হলো যথাক্রমে x ও y (যেখানে, x > y)।
∴ এবং
প্রদত্ত,
‘1’ + ‘2’ নং সমীকরণ যোগ করে পাই,
‘1’ নং সমীকরণে x = 81° বসিয়ে পাই,
উত্তর : সমকোণী ত্রিভুজটির সূক্ষকোণ দুটির ষষ্ঠিক মান হলো যথাক্রমে 81° ও 9°।
koshe dekhi 20 class 10
Q5. একটি ত্রিভুজের একটি কোণের পরিমাপ 65° এবং দ্বিতীয়টির পরিমাপ হলে, তৃতীয় কোণটির ষষ্টিক ও বৃত্তীয় মান হিসাব করে লিখি।
সমাধান :
∴ ত্রিভুজটির কোণ দুটির সমষ্টি = (65 + 15)° ⇒ 80°
সুতরাং, ত্রিভুজটির তৃতীয় কোনটির ষষ্ঠিক মান = 180° − 80° ⇒ 100°
100° এর বৃত্তীয় মান হলো =
উত্তর : ত্রিভুজটির তৃতীয় কোণটির ষষ্ঠিক মান ও বৃত্তীয় মান হলো যথাক্রমে 100° ও .
koshe dekhi 20 class 10
Q6. দুটি কোণের সমষ্টি 135° এবং তাদের অন্তর , হলে, কোণ দুটির ষষ্টিক ও বৃত্তীয় মান হিসাব করে। লিখি।
সমাধান :
ধরি, কোণ দুটির মান হলো যথাক্রমে x ও y (যেখানে, x > y)।
প্রশ্নানুযায়ী, \( x+y=135°\; \; ……\: (1) \) এবং
\( x-y=\frac{\pi^c }{12}\Rightarrow \frac{180°}{12}\Rightarrow 15°\; \; \; \; [ \because \pi^c=180°] \)
\( \therefore x-y=15° \; \; \; ……\: \left ( 2 \right ) \)
‘1’ + ‘2’ নং সমীকরণ যোগ করে পাই,
\( \therefore ( x+y )+ ( x-y )=135° + 15° \)
\( \Rightarrow x+y+x-y=150° \)
\( \Rightarrow 2x=150° \)
\( \Rightarrow x=\frac{150°}{2} \Rightarrow 75° \)
\( \therefore x=75° \)
‘1’ নং সমীকরণে x = 75° বসিয়ে পাই,
\( x + y = 135° \)
\( ⇒ 75° + y = 135° \)
\( ⇒ y = 135° − 75° \)
\( ∴ y = 60° \)
∴ এখন, 75° এর বৃত্তীয় মান = \( (75°\times \frac{\pi^c}{180} )\Rightarrow \frac{5 \pi ^c}{12}\; \; \; [ \because x°= ( x\times \frac{\pi ^c}{180°})] \)
এবং, 60° এর বৃত্তীয় মান = \( (60°\times \frac{\pi^c}{180} )\Rightarrow \frac{ \pi ^c}{3} \)
উত্তর : নির্ণেয় কোন দুটির ষষ্ঠিক মান হলো 75° ও 60° এবং বৃত্তীয় মান হলো যথাক্রমে \( \frac{5\pi^c}{12} \) ও \( \frac{\pi^c}{3} \).
koshe dekhi 20 class 10
Q7. একটি ত্রিভুজের কোণ তিনটির অনুপাত 2:3:4 হলে, ত্রিভুজটির বৃহত্তম কোণটির বৃত্তীয় মান হিসাব করে লিখি।
সমাধান :
ধরি, তিনটি কোনের মান যথাক্রমে 2x, 3x এবং 4x.
∵ ত্রিভুজের তিনটি কোনের সমষ্টি 180° এর সমান।
∴ 2x + 3x + 4x = 180°
বা, 9x = 180°
বা, x = 20°
∴ বৃহত্তম কোনটির ষষ্টিক মান =
∴ বৃহত্তম কোনটির (অর্থাৎ, 80°) বৃত্তীয় মান –
(Answer)
koshe dekhi 20 class 10
Q8. একটি বৃত্তের ব্যাসার্ধের দৈঘ্য 28 সেমি.। এই বৃত্তে 5.5 সেমি. দৈর্ঘ্যের বৃত্তচাপ দ্বারা ধৃত কেন্দ্রীয় কোণটির বৃত্তীয় মান হিসাব করে লিখি।
সমাধান :
আমরা জানি, 
[∵ বৃত্তের পরিধি = 2π × ব্যাসার্ধ]
এর বৃত্তীয় মান =
উত্তর : 5.5 cm. বৃত্তচাপ বৃত্তের কেন্দ্রে যে কোন উৎপন্ন করে তার বৃত্তীয় মান ।
koshe dekhi 20 class 10
Q9. একটি বৃত্তের অসমান দৈর্ঘ্যের দুটি চাপ কেন্দ্রে যে কোণ ধারণ করে আছে তার অনুপাত 5:2 এবং দ্বিতীয় কোণটির ষষ্টিক মান 30° হলে, প্রথম কোণটির ষষ্টিক মান ও বৃত্তীয় মান হিসাব করে লিখি।
সমাধান :
ধরি, প্রথম কোণটির ষষ্ঠিক মান x°
প্রশ্নানুযায়ী,
∴ এখন, 75° এর বৃত্তীয় মান =
উত্তর : প্রথম কোণটির ষষ্ঠিক মান ও বৃত্তীয় মান হলো যথাক্রমে 75° ও
Q10. একটি ঘূর্ণায়মান রশ্মি কোণ উৎপন্ন করেছে। রশ্মিটি কোনদিকে কতবার পূর্ণ আবর্তন করেছে এবং তারপরে আরও কত ডিগ্রি কোণ উৎপন্ন করেছে তা হিসাব করে লিখি।
সমাধান :
∵ প্রদত্ত, কোণটির মান ঋণাত্মক।
∴ রশ্মিটি ঘড়ির কাঁটার দিকে ঘুরছে। (Answer)
প্রদত্ত,
∵ 1 টি পূর্ণ আবর্তন করার অর্থ হলো 360° কোণ পরিক্রমণ করা।
∴

উত্তর : রশ্মিটি 2 বার পূর্ণ আবর্তন করার পর আরো 195° কোণ উৎপন্ন করেছে।
Q11. ABC একটি সমদ্বিবাহু ত্রিভূজ অঙ্কন করেছি যার সমান বাহুদ্বয়ের অন্তর্ভুত কোণ ;
এর সমদ্বিখণ্ডক AC বাহুকে D বিন্দুতে ছেদ করেছে।
এবং
এর বৃত্তীয় মান নির্ণয় করি।
সমাধান :
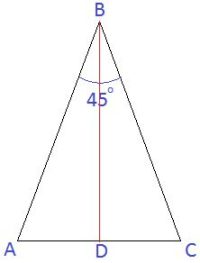
∵ ABC একটি সমদ্বিবাহু ত্রিভুজ, যার AB = BC
∴ এখন, এর বৃত্তীয় মান =
আবার, ∵ BD হলো এর সমদ্বিখণ্ডক।
∴ এখন, এর বৃত্তীয় মান =
উত্তর : ও
এর প্রত্যেকটির বৃত্তীয় মান
এবং
ও
এর প্রত্যেকটির বৃত্তীয় মান
Q12. ABC সমবাহু ত্রিভুজের BC ভূমিকে E বিন্দু পর্যন্ত এমনভাবে বর্ধিত করলাম যেন CE = BC হয়। A, E যুক্ত করে ACE ত্রিভুজের কোণগুলির বৃত্তীয় মান নির্ণয় করি।
সমাধান :
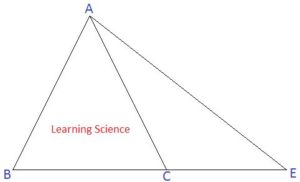
∵ ABC হলো সমবাহু ত্রিভুজ।
∴ AB = BC = AC এবং প্রতিটি কোণের মান 60° অর্থাৎ
আবার, ∵ প্রদত্ত BC = CE
∴ AC = CE [∵ BC = AC]
সুতরাং, ΔACE হলো সমদ্বিবাহু ত্রিভুজ যার AC = CE.
∴
এখন,
∴ এখন, 120° এর বৃত্তীয় মান = (Answer)
সুতরাং,
∴ এখন, 30° এর বৃত্তীয় মান = (Answer)
উত্তর : ΔACE এর এবং
.
Q13. কোনো চতুর্ভুজের তিনটি কোণের পরিমাপ যথাক্রমে ও 90° হলে, চতুর্থ কোণটির ষষ্টিক ও বৃত্তীয় মান হিসাব করে লিখি।
সমাধান :
এবং,
∵ চতুর্ভুজের চারটি কোণের সমষ্টি 360°.
∴ চতুর্ভুজের চতুর্থ কোনটির ষষ্টিক মান = 360° − (60 + 150 + 90)° ⇒ 60° এবং বৃত্তীয় মান . (Answer)
Q14. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.) :
(A) বহুবিকল্পীও প্রশ্ন (M.C.Q.)
(i) একটি ঘড়ির মিনিটের কাঁটার প্রান্তবিন্দু 1 ঘন্টায় আবর্তন করে
(a) রেডিয়ান
(b) রেডিয়ান
(c) রেডিয়ান
(d) রেডিয়ান
ঘড়ির মিনিটের কাঁটার প্রান্তবিন্দু 1 ঘন্টায় = 360° আবর্তন করে।
∴ এখন, 360° এর বৃত্তীয় মান (উত্তর – d)
Q14. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.) :
(A) বহুবিকল্পীও প্রশ্ন (M.C.Q.)
(ii) রেডিয়ান সমান
(a) 60°
(b) 45°
(c) 90°
(d) 30°
সমাধান : (d) 30°
(উত্তর – d)
Q14. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.) :
(A) বহুবিকল্পীও প্রশ্ন (M.C.Q.)
(iv) s = rθ সম্পর্কে θ -এর পরিমাপ করা হয়
(a) ষষ্টিক পদ্ধতিতে
(b) বৃত্তীয় পদ্ধতিতে
(c) ওই দুই পদ্ধতিতে
(d) ওই দুই পদ্ধতির কোনোটিতেই নয়।
সমাধান : (b) বৃত্তীয় পদ্ধতিতে (উত্তর – b)
Q14. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A.) :
(A) বহুবিকল্পীও প্রশ্ন (M.C.Q.)
(v) ABCD বৃত্তস্থ চতুর্ভুজের হলে,
-এর বৃত্তীয় মান
(a)
(b)
(c)
(d)
সমাধান :
আমরা জানি, বৃত্তস্থ চতুর্ভুজের বিপরীত কোণ দুটির সমষ্টি 180° এর সমান।
∴ এখন, 60° এর বৃত্তীয় মান = (উত্তর – a)
Q.14 (B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি :
(i) একটি রশ্মির প্রান্তবিন্দুকে কেন্দ্র করে রশ্মিটির ঘড়ির কাঁটার বিপরীত দিকে ঘোরার জন্য উৎপন্ন কোনটি ধনাত্মক।
সমাধান : সত্য।
Note : রশ্মিকে ঘড়ির কাঁটার বিপরীত দিকে ঘোরানোর ফলে যে কোণ সৃষ্টি হয় তার মানকে ধনাত্মক ধরা হয়।
Q.14 (B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি :
(ii) একটি রশ্মির প্রান্তবিন্দুকে কেন্দ্র করে রশ্মিটির ঘড়ির কাঁটার দিকে দু-বার আবর্তনের জন্য 720° কোন উৎপন্ন হয়।
সমাধান : মিথ্যা।
সঠিক উত্তর হবে = − 720°
Note : রশ্মিকে ঘড়ির কাঁটার দিকে ঘোরানোর ফলে যে কোণ সৃষ্টি হয় তার মানকে ঋণাত্মক ধরা হয়।
Q.14 (C) শুন্যস্থান পূরণ করি :
(i) π রেডিয়ান একটি _______ কোণ।
সমাধান : π রেডিয়ান একটি বৃত্তীয় কোণ।
Q.14 (C) শুন্যস্থান পূরণ করি :
(ii) ষষ্ঠিক পদ্ধতিতে 1 রেডিয়ান সমান _______ (প্রায়)।
সমাধান : ষষ্ঠিক পদ্ধতিতে 1 রেডিয়ান সমান 57.3° (প্রায়)।
Q.14 (C) শুন্যস্থান পূরণ করি :
(iii) পরিমাপের কোনটির সম্পূরক কোণের বৃত্তীয় মান ______।
সমাধান : পরিমাপের কোনটির সম্পূরক কোণের বৃত্তীয় মান
।
∵ দুটি কোণের সমষ্টি 180° বা এর সমান হলে কোণ দুটিকে পরস্পরের সম্পূরক কোণ বলা হয়।
∴ পরিমাপের কোনটির সম্পূরক কোণের বৃত্তীয় মান হবে,
Q15. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A)
(i) একটি কোণের ডিগ্রিতে মান D এবং ওই কোণের রেডিয়ানে মান R হলে, -এর মান নির্ণয় করি।
সমাধান :
এখন, প্রশ্নানুযায়ী,
উত্তর : নির্ণেয় -এর মান
।
Q15. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A)
(ii) 63°35’15” পরিমাপের কোণটির পূরক কোণের মান লিখি।
সমাধান :
∵ দুটি কোণের সমষ্টি 90° এর সমান হলে কোণ দুটিকে পরস্পরের পূরক কোণ বলা হয়।
∴ 63°35’15” পরিমাপের কোণটির পূরক কোণের মান হবে,
উত্তর : নির্ণেয় 63°35’15” পরিমাপের কোণটির পূরক কোণের মান ।
Q15. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A)
(iii) একটি ত্রিভুজের দুটি কোণের পরিমাপ 65°56’55” এবং 64°3’5″ হলে, তৃতীয় কোণটির বৃত্তীয় মান নির্ণয় করি।
সমাধান :
∵ ত্রিভুজের তিনটি কোণের সমষ্টি 180° এর সমান।
∴ ত্রিভুজটির তৃতীয় কোনটির ষষ্টিক মান হবে
∴ এখন, 50° এর বৃত্তীয় মান =
উত্তর : নির্ণেয় তৃতীয় কোণটির বৃত্তীয় মান ।
Q15. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A)
(iv) একটি বৃত্তে 220 সেমি. দৈর্ঘ্যের বৃত্তচাপ বৃত্তের কেন্দ্রে 63° পরিমাপের কোণ উৎপন্ন করলে, বৃত্তের ব্যাসার্ধের দৈর্ঘ্য নির্ণয় করি।
সমাধান :
ধরি, বৃত্তটির ব্যাসার্ধ r সেমি.।
আমরা জানি, 
[∵ বৃত্তের পরিধি = 2πr]
সেমি.।
উত্তর : নির্ণেয় বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 200 সেমি.।
Q15. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A)
(v) একটি ঘড়ির ঘন্টার কাঁটার প্রান্তবিন্দু 1 ঘন্টা আবর্তনে যে পরিমাণ কোণ উৎপন্ন করে তার বৃত্তীয় মান লিখি।
সমাধান :
আমরা জানি, ঘড়ির ঘণ্টার কাঁটা 12 ঘণ্টায় 360° কোণ উৎপন্ন করে।
∴ ঘড়ির ঘণ্টার কাঁটা 1 ঘণ্টায় অর্থাৎ
কোণ উৎপন্ন করবে।
∴ এখন, 30° এর বৃত্তীয় মান = (উত্তর)
উত্তর : নির্ণেয় কোনটির বৃত্তীয় মান ।

Thank you
mst wlcm
Koi
Thank you
mst wlcm
Thank you so much
mst wlcm
Thanks
Thanks for your valuable comment.
Please keep visiting our website learningscience.co.in and also visit our youtube channel youtube.com/c/scienceduniyainbangla.
Thanks a lot
My Pleasure. Thank you.