Koshe dekhi 8 class 10

Q1. পাশের চিত্রের ঘনবস্তুটি দেখি ও নীচের প্রশ্নের উত্তর লিখি। লম্ব বৃত্তাকার চোঙ

(i) ছবির ঘনবস্তুটির ______ টি তল।

উত্তরঃ 3 টি তল।

(ii) ছবির ঘনবস্তুটির _______ টি বক্রতল ও _______ টি সমতল।

উত্তরঃ 1 টি বক্রতল ও 2 টি সমতল।

Q2. আমার বাড়ির 5টি ঘনবস্তুর নাম লিখি যাদের আকার লম্ব বৃত্তাকার চোঙ।

উত্তরঃ আমার বাড়ির 5টি ঘনবস্তু যাদের আকার লম্ব বৃত্তাকার চোঙঃ গ্যাস সিলিন্ডার, জলের পাইপ, টিউব লাইট, বেলন, গোলাকার থাম।

Q3. স্টিলের পাতলা চাদর দিয়ে তৈরি ঢাকনা সমেত একটি ড্রামের ব্যাসের দৈর্ঘ্য 28 সেমি.। ড্রামটি তৈরি করতে যদি 2816 বর্গসেমি. চাদর লাগে তবে ড্রামটির উচ্চতা হিসাব করে লিখি।

সমাধানঃ

ধরি,

ড্রামটির ব্যাসার্ধ = r সেমি. ও উচ্চতা = h সেমি.।

প্রদত্ত,

ড্রামের ব্যাসের দৈর্ঘ্য (2r) = 28 সেমি.।

∴ ড্রামটির ব্যাসার্ধ $\left ( r \right )=\frac{28}{2}=14$ সেমি.।

ড্রামটি তৈরি করতে চাদর লাগে 2816 বর্গসেমি.।

অর্থাৎ, ড্রামটির সমগ্রতলের ক্ষেত্রফল = 2816 বর্গসেমি.।

$\therefore 2\pi r\left ( r+h \right )=2816$

বা, $2\times \frac{22}{7}\times 14\left ( 14+h \right )=2816$

বা, $88\left ( 14+h \right )=2816$

বা, $\left ( 14+h \right )=\frac{2816}{88}=32$

$\therefore h=32-14=18$

উত্তরঃ নির্ণেয় ড্রামটির উচ্চতা 18 সেমি।

Q4. একটি ঘরের বারান্দায় 5.6 ডেসিমি. ব্যাসের এবং 2.5 মিটার.লম্ব দুটি লম্ব বৃত্তাকার পিলার ঢালাই করতে কত ঘনডেসিমি. মশলা লাগবে হিসাব করে লিখি। প্রতি বর্গমিটার 125 টাকা হিসাবে পিলার দুটি প্লাস্টার করতে কত খরচ হবে হিসাব করি।

সমাধানঃ

প্রদত্ত,

লম্ব বৃত্তাকার পিলারের ব্যাসের দৈর্ঘ্য (2r) = 5.6 ডেসিমি.।

∴ পিলারটির ব্যাসার্ধ $\inline \left ( r \right )=\frac{5.6}{2}=2.8$ ডেসিমি. ও

উচ্চতা (h) = 2.5 মিটার $\inline =2.5\times 10=25$ ডেসিমি.

লম্ব বৃত্তাকার পিলার দুটির আয়তন –

$=2\times \pi r^{2}h$

$=2\times \frac{22}{7}\times \left ( 2.8 \right )^{2}\times 25$

$=\frac{2\times 22\times 28\times 28\times 25}{7\times 10\times 10}$

$=1232$ ঘনডেসিমি.

∴ পিলার দুটি ঢালাই করতে 1232 ঘনডেসিমি. মশলা লাগবে। (উত্তর)

পিলার দুটির বক্রতলের ক্ষেত্রফল –

$=2\times 2\pi rh$ বর্গ ডেসিমি. ।

$=2\times 2\times \frac{22}{7}\times 2.8\times 25$

$=\frac{2\times 2\times 22\times 28\times 25}{7\times 10}$

$=880$ বর্গ ডেসিমি.

$=\frac{880}{100}$ বর্গমিটার

$=8.8$ বর্গমিটার।

প্রতি বর্গমিটার 125 টাকা হিসাবে পিলার দুটি প্লাস্টার করতে খরচ হবে $=8.8\times 125=1100$ টাকা।

উত্তরঃ নির্ণেয় পিলার দুটি ঢালাই করতে 1232 ঘনডেসিমি. মশলা লাগবে এবং পিলার দুটি প্লাস্টার করতে মোট 1100 টাকা খরচ হবে।

Q5. 2.8 ডেসিমি দৈর্ঘ্যের অন্তর্ব্যাসবিশিষ্ট এবং 7.5 ডেসিমি. লম্বা একটি জ্বালানি গ্যাস সিলিন্ডারে 15.015 কিগ্রা. গ্যাস থাকলে, প্রতি ঘন ডেসিমি. গ্যাসের ওজন হিসাব করে লিখি।

সমাধানঃ

প্রদত্ত,

সিলিন্ডারের অন্তর্ব্যাসের দৈর্ঘ্য (2r) = 2.8 ডেসিমি.।

∴ সিলিন্ডারের ব্যাসার্ধ $\left ( r \right )=\frac{2.8}{2}=1.4$ ডেসিমি. ও

উচ্চতা (h) = 7.5 ডেসিমি.।

জ্বালানি গ্যাস সিলিন্ডারের আয়তন,

$=\pi r^{2}h$

$=\frac{22}{7}\times \left ( 1.4 \right )^{2}\times 7.5$

$=\frac{22\times 14\times 14\times 75}{7\times 10\times 10\times 10}$

$=46.2$ ঘন ডেসিমি.

∴ প্রতি ঘন ডেসিমি. গ্যাসের ওজন

$=\frac{15.015}{46.2}=0.325$ কিগ্রা

$=0.325\times 1000=325$ গ্রাম।

উত্তরঃ নির্ণেয় সিলিন্ডারে প্রতি ঘন ডেসিমি. গ্যাসের ওজন 325 গ্রাম।

Q6. সমান ব্যাস ও সমান উচ্চতা বিশিষ্ট তিনটি জারের প্রথমটির ${\color{Blue} \frac{2}{3}}$ অংশ, দ্বিতীয়টির ${\color{Blue} \frac{5}{6}}$ অংশ ও তৃতীয়টির ${\color{Blue} \frac{7}{9}}$ অংশ লঘু সালফিউরিক অ্যাসিডে পূর্ণ ছিল। ওই তিনটি জারের অ্যাসিড যদি 2.1 ডেসিমি. দৈর্ঘ্যের ব্যাসের একটি জারে রাখা হয়, তবে জারে অ্যাসিডের উচ্চতা 4.1 ডেসিমি. হয়। প্রথম তিনটি জারের ব্যাসের দৈর্ঘ্য 1.4 ডেসিমি. হলে, তাদের উচ্চতা হিসাব করে লিখি।

সমাধানঃ

ধরি, প্রথম তিনটি জারের প্রত্যেকটির উচ্চতা = h ডেসিমি.।

প্রদত্ত,

প্রত্যেকটির ব্যাসের দৈর্ঘ্য (2r) = 1.4 ডেসিমি.।

∴ প্রত্যেকটির ব্যাসার্ধ $\left ( r \right )=\frac{1.4}{2}=\frac{14}{2\times 10}=\frac{14}{20}$ ডেসিমি.।

বড়ো জারটির ব্যাসের দৈর্ঘ্য (2R) = 2.1 ডেসিমি.।

∴ বড়ো জারটির ব্যাসার্ধ $\left ( R \right )=\frac{2.1}{2}=\frac{21}{2\times 10}=\frac{21}{20}$ ডেসিমি.।

বড়ো জারটির উচ্চতা ( H) = 4.1 ডেসিমি.।

∴ প্রথম তিনটি জারে মোট অ্যাসিডের আয়তন

$=\pi r^{2}\left ( \frac{2h}{3} \right )+\pi r^{2}\left ( \frac{5h}{6} \right )+\pi r^{2}\left ( \frac{7h}{9} \right )$

$=\pi r^{2}h\left ( \frac{2}{3}+\frac{5}{6}+\frac{7}{9} \right )$

$=\frac{22}{7}\times \left ( \frac{14}{20} \right )^{2}\times h\times \left ( \frac{12+15+14}{18} \right )$

$=\frac{22\times 14\times 14\times h\times 41}{7\times 20\times 20\times 18}$

$=\frac{77\times 41}{50\times 18}\times h$ ঘন ডেসিমি.

∴ বড়ো জারটির আয়তন

$=\pi R^{2}H$

$=\frac{22}{7}\times \left ( \frac{21}{20} \right )^{2}\times 4.1$

$=\frac{22\times 21\times 21\times 41}{7\times 20\times 20\times 10}$ ঘন ডেসিমি.

প্রশ্নানুসারে,

প্রথম তিনটি জারে মোট অ্যাসিডের আয়তন = বড়ো জারটির আয়তন

বা, $\frac{77\times 41}{50\times 18}\times h$ $=\frac{22\times 21\times 21\times 41}{7\times 20\times 20\times 10}$

বা, $h=\frac{22\times 21\times 21\times 41\times 50\times 18}{7\times 20\times 20\times 10\times 77\times 41}$

$\therefore h=\frac{81}{20}=4.05$

উত্তরঃ নির্ণেয় প্রথম তিনটি জারের প্রত্যেকটির উচ্চতা 4.05 ডেসিমি.।

Q7. একমুখ খোলা একটি লম্ব বৃত্তাকার পাত্রের সমগ্রতলের ক্ষেত্রফল 2002 বর্গ সেমি.। পাত্রটির ভূমির ব্যাসের দৈর্ঘ্য 14 সেমি. হলে, পাত্রটিতে কত লিটার জল ধরবে হিসাব করে লিখি।

সমাধানঃ

ধরি, পাত্রটির উচ্চতা = h সেমি।

প্রদত্ত,

পাত্রটির ব্যাসের দৈর্ঘ্য (2r) = 14 সেমি.।

∴ পাত্রটির ব্যাসার্ধ $\left ( r \right )=\frac{14}{2}=7$ সেমি.।

আমরা জানি,

একমুখ খোলা পাত্রের সমগ্রতলের ক্ষেত্রফল

$=\pi r^{2}+2\pi rh$

প্রশ্নানুসারে,

$\pi r^{2}+2\pi rh=2002$

বা, $\frac{22}{7}\times \left ( 7 \right )^{2}+2\times \frac{22}{7}\times 7\times h=2002$

বা, $154+44h=2002$

বা, $44h=2002-154$

বা, $44h=1848$

$\therefore h=\frac{1848}{44}=42$

∴ পাত্রটির উচ্চতা = 42 সেমি $=\frac{42}{10}$ ডেসিমি. ও

ব্যাসার্ধ $=7$ সেমি $=\frac{7}{10}$ ডেসিমি।

∴ পাত্রটির আয়তন $=\pi r^{2}h$

$=\frac{22}{7}\times \left ( \frac{7}{10} \right )^{2}\times \frac{42}{10}$

$=\frac{22\times 7\times 7\times 42}{7\times 10\times 10\times 10}$

$=6.468$ ঘন ডেসিমি.

$=6.468$ লিটার। [ ${\color{Blue} \because }$ 1 ঘন ডেসিমি. = 1 লিটার ]

উত্তরঃ নির্ণেয় পাত্রটিতে 6.468 লিটার জল ধরবে।

Q8. যদি 14 সেমি. ব্যাসের পাইপযুক্ত একটি পাম্পসেট মিনিটে 2500 মিটার জল সেচ করতে পারে, তাহলে ওই পাম্পটি 1 ঘন্টায় কত কিলোলিটার জলসেচ করবে, হিসাব করে লিখি।

[ 1 লিটার = 1 ঘন ডেসিমি. ]

সমাধানঃ

পাম্পসেটটির পাইপের ব্যাস (2r) = 14 সেমি.

∴ পাইপের ব্যাসার্ধ $\left ( r \right )=\frac{14}{2}=7$ সেমি. $=\frac{7}{10}$ ডেসিমি.।

$\because$ পাইপটি মিনিটে জলসেচ করে ( h ) = 2500 মিটার = 25000 ডেসিমি.।

∴ পাইপটি 1 ঘণ্টায় জলসেচ করে

$=\pi r^{2}h\times 60$ [ ${\color{Blue} \because }$ 1 ঘণ্টা = 60 মিনিট ]

$=\frac{22}{7}\times \left ( \frac{7}{10} \right )^{2}\times 25000\times 60$

$=\frac{22\times 7\times 7\times 25000\times 60}{7\times 10\times 10}$

$=2310000$ ঘন ডেসিমি.

= 2310000 লিটার

= 2310 কিলোলিটার।

উত্তরঃ নির্ণেয় পাইপটি 1 ঘণ্টায় 2310 কিলোলিটার জলসেচ করবে।

Q9. 7 সেমি. ব্যাসের একটি লম্বা গ্যাসজারে কিছু জলে আছে। ওই জল যদি 5.6 সেমি. দৈর্ঘ্যের ব্যাসের 5 সেমি. লম্বা একটি নিরেট লোহার লম্ব বৃত্তাকার চোঙাকৃতি টুকরো সম্পূর্ণ ডোবানো যায়, তবে জলতল কতটুকু উপরে উঠবে হিসাব করে লিখি।

সমাধানঃ

প্রদত্ত,

লম্ব বৃত্তাকার চোঙাকৃতি টুকরোটির ব্যাস (2r) = 5.6 সেমি.

∴ ব্যাসার্ধ (r) $=\frac{5.6}{2}=2.8$ সেমি. ও

উচ্চতা (h) = 5 সেমি.।

∴ লম্ব বৃত্তাকার চোঙের আয়তন

$=\pi r^{2}h$

$=\pi \left ( 2.8 \right )^{2}\times 5$ ঘনসেমি.

আবার,

গ্যাস জারের ব্যাস (2R) = 7 সেমি.

∴ ব্যাসার্ধ (R) $=\frac{7}{2}$ সেমি.।

ধরি, গ্যাস জারটিতে জলতল $x$ সেমি ওপরে উঠবে।

∴ গ্যাস জারের আয়তন

$=\pi \left ( \frac{7}{2} \right )^{2}\times x$ ঘনসেমি.

প্রশ্নানুসারে,

গ্যাস জারের আয়তন = লম্ব বৃত্তাকার চোঙের আয়তন

বা, $\pi \times \left ( \frac{7}{2} \right )^{2}\times x=\pi \times \left ( 2.8 \right )^{2}\times 5$

বা, $\pi \times \frac{7}{2} \times \frac{7}{2} \times x=\pi \times \frac{28}{10}\times \frac{28}{10}\times 5$

বা, $x=\frac{28}{10}\times \frac{28}{10}\times 5\times \frac{2}{7}\times \frac{2}{7}$

$\therefore x=\frac{32}{10}=3.2$

উত্তরঃ নির্ণেয় গ্যাসজারে জলতল 3.2 সেমি ওপরে উঠবে।

Q10. একটি লম্ব চোঙাকৃতি স্তম্ভের বক্রতলের ক্ষেত্রফল 264 বর্গ মিটার এবং আয়তন 924 ঘন মিটার হলে, এই স্তম্ভের ব্যাসের দৈর্ঘ্য ও উচ্চতা হিসাব করে লিখি।

সমাধানঃ

ধরি, লম্ব চোঙাকৃতি স্তম্ভের ব্যাসের দৈর্ঘ্য 2r মিটার ও উচ্চতা h মিটার।

প্রদত্ত,

স্তম্ভের বক্রতলের ক্ষেত্রফল $\left (2\pi rh \right )=264$ বর্গ মিটার

$\therefore \pi rh =\frac{264}{2}=132$ বর্গ মিটার…….(i)

এবং

আয়তন $\left (\pi r^{2}h \right )=924$ ঘন মিটার।

বা, $\pi rh\times r=924$

বা, $132\times r=924$ [ (i) থেকে πrh এর মান বসিয়ে পাই ]

$\therefore r=\frac{924}{132}=7$

$\therefore 2r=7\times 2=14$

(i) নং সমীকরণে r এর মান বসিয়ে পাই

$\frac{22}{7}\times 7\times h=132$

$22h=132$

$\therefore h=\frac{132}{22}=6$

উত্তরঃ নির্ণেয় লম্ব চোঙাকৃতি স্তম্ভের ব্যাসের দৈর্ঘ্য 14 মিটার ও উচ্চতা 6 মিটার।

Q11. 9 মিটার উচ্চতা বিশিষ্ট একটি লম্ব বৃত্তাকার চোঙাকৃতি ট্যাঙ্ক জলপূর্ণ আছে। 6 সেমি দৈর্ঘ্যের ব্যাসের একটি পাইপ দিয়ে মিনিটে 225 মিটার বেগে জল বের হয়, তাহলে 36 মিনিটে ট্যাঙ্কটির সমস্ত জল বেরিয়ে যায়। ট্যাঙ্কটির ব্যাসের দৈর্ঘ্য হিসাব করে লিখি।

সমাধানঃ

ধরি, ট্যাঙ্কটির ব্যাসের দৈর্ঘ্য 2R মিটার।

প্রদত্ত,

লম্ব বৃত্তাকার চোঙাকৃতি ট্যাঙ্কের উচ্চতা (H) = 9 মিটার।

পাইপটির ব্যাস, $2r=6$ সেমি $=\frac{6}{100}$ মিটার।

∴ পাইপটির ব্যাসার্ধ (r) $=\frac{6}{100\times 2}=\frac{3}{100}$ মিটার।

পাইপটি দিয়ে 36 মিনিটে জল বার হয়-

$=\pi r^{2}h$

$=\pi \left ( \frac{3}{100} \right )^{2}\times 225\times 36$ ঘন মিটার।

প্রশ্নানুসারে,

$\pi R^{2}\times 9=\pi \left ( \frac{3}{100} \right )^{2}\times 225\times 36$

বা, $R^{2}\times 9=\left ( \frac{3}{100} \right )^{2}\times 225\times 36$

বা, $R^{2}=\frac{3\times 3\times 225\times 36}{100\times 100\times 9}$

বা, $R^{2}=\frac{9\times 9}{10\times 10}$

বা, $R^{2}=\left ( \frac{9}{10} \right )^{2}$

$\therefore R=\frac{9}{10}$

∴ ব্যাস $=2R=2\times \frac{9}{10}=\frac{18}{10}=1.8$ মিটার।

উত্তরঃ নির্ণেয় ট্যাঙ্কটির ব্যাসের দৈর্ঘ্য 1.8 মিটার।

Q12. সমান ঘনত্বের একটি লম্ববৃত্তাকার কাঠের গুড়ির বক্রতলের ক্ষেত্রফল 440 বর্গ ডেসিমি.। এক ঘনডেসিমি. কাঠের ওজন 1.5 কিগ্রা. এবং গুড়িটির ওজন 9.24 কুইন্টাল হলে, গুড়িটির ব্যাসের দৈর্ঘ্য ও উচ্চতা হিসাব করে লিখি।

সমাধানঃ

ধরি, গুড়িটির ব্যাসার্ধ = r ডেসিমি. ও

উচ্চতা = h ডেসিমি.।

প্রদত্ত,

লম্ববৃত্তাকার কাঠের গুড়ির বক্রতলের ক্ষেত্রফল = 440 বর্গ ডেসিমি.।

∴ $2\pi rh=440$ ……. (i)

গুড়িটির ওজন = 9.24 কুইন্টাল = 9.24 × 100 = 924 কিগ্রা।

$\because$ এক ঘনডেসিমি. কাঠের ওজন 1.5 কিগ্রা.।

∴ গুড়িটির আয়তন $\left ( \pi r^{2}h \right )$

$=\frac{924}{1.5}=\frac{924\times 10}{15}=616$ ঘন ডেসিমি.।

$\pi r^{2}h=616$ ……… (ii)

এখন,

(ii) নং সমীকরণকে (i) নং সমীকরণ দ্বারা ভাগ করে পাই,

$\frac{\pi r^{2}h}{2\pi rh}=\frac{616}{440}$

বা, $\frac{r}{2}=\frac{7}{5}$

বা, $r=\frac{2\times 7}{5}=\frac{14}{5}$

$\therefore r=2.8$

∴ গুড়িটির ব্যাস = 2×2.8 = 5.6 ডেসিমি.।

(i) নং সমীকরণে r এর মান বসিয়ে পাই

$2\times \frac{22}{7}\times \frac{28}{10}\times h=440$

বা, $h=\frac{440\times 7\times 10}{2\times 22\times 28}$

$\therefore h=25$ ডেসিমি.

উত্তরঃ নির্ণেয় গুড়িটির ব্যাসের দৈর্ঘ্য 5.6 ডেসিমি. ও উচ্চতা 25 ডেসিমি.।

Q13. দুই মুখ খোলা একটি লম্ব বৃত্তাকার লোহার পাইপের মুখের বহির্ব্যাসের দৈর্ঘ্য 30 সেমি.। অন্তর্ব্যাসের দৈর্ঘ্য 26 সেমি. এবং পাইপটির দৈর্ঘ্য 14.7 মিটার। প্রতি বর্গ ডেসিমি. 2.25 টাকা হিসাবে ওই পাইপটির সমগ্রতলে আলকাতরার প্রলেপ দিতে কত খরচ হবে, তা হিসাব করে লিখি।

সমাধানঃ

$\because$ পাইপটির বহির্ব্যাসের দৈর্ঘ্য 30 সেমি.।

∴ বহির্ব্যাসার্ধ $\left ( R \right )=\frac{30}{2}$ সেমি. $=\frac{15}{10}$ ডেসিমি.।

$\because$ অন্তর্ব্যাসের দৈর্ঘ্য 26 সেমি.।

∴ অন্তর্ব্যাসার্ধ $\left ( r \right )=\frac{26}{2}$ সেমি. $=\frac{13}{10}$ ডেসিমি.।

পাইপটির দৈর্ঘ্য (h) = 14.7 মিটার =14.7 × 10 =147 ডেসিমি.।

∴ পাইপটির বাইরের ক্ষেত্রফল $=2\pi Rh=2\times \frac{22}{7}\times \frac{15}{10}\times 147=1386$ বর্গ ডেসিমি.।

পাইপটির ভেতরের ক্ষেত্রফল $=2\pi rh=2\times \frac{22}{7}\times \frac{13}{10}\times 147=1201.2$ বর্গ ডেসিমি.।

পাইপটির দুই ধারের বৃত্তাকার অংশের ক্ষেত্রফল

$=2\pi \left ( R^{2}-r^{2} \right )$ বর্গ ডেসিমি.

$=2 \times \frac{22}{7}\times \left \{ \left ( \frac{15}{10} \right )^{2}-\left ( \frac{13}{10} \right )^{2} \right \}$

$=2\times \frac{22}{7}\times \left ( \frac{225}{100} -\frac{169}{100}\right )$

$=2\times \frac{22}{7}\times \frac{56}{100}$

$=\frac{352}{100}$

$=3.52$ বর্গ ডেসিমি.

∴ পাইপটির সমগ্রতলের ক্ষেত্রফল

$=\left ( 1386+1201.2+3.52 \right )=2590.72$ বর্গ ডেসিমি.।

∴ প্রতি বর্গ ডেসিমি. 2.25 টাকা হিসাবে সমগ্র পাইপটি আলকাতরার প্রলেপ দিতে খরচ হবে

$=2590.72\times 2.25=5829.12$ টাকা।

উত্তরঃ নির্ণেয় পাইপটির সমগ্রতলে আলকাতরার প্রলেপ দিতে 5829.12 টাকা খরচ হবে।

Koshe dekhi 8 class 10

Q14. একটি দুই মুখ খোলা লোহার লম্ববৃত্তাকার ফাপা চোঙের উচ্চতা 2.8 মিটার। চোঙটির অন্তর্ব্যাসের দৈর্ঘ্য 4.6 ডেসিমি. এবং চোঙটি 84.48 ঘন ডেসিমি. লোহা দিয়ে তৈরি হলে, চোঙটির বহির্ব্যাসের দৈর্ঘ্য নির্ণয় করি।

সমাধানঃ

প্রদত্ত,

চোঙটির উচ্চতা (h) = 2.৪ মিটার = 28 ডেসিমি.।

চোঙটির অন্তর্ব্যাসের দৈর্ঘ্য (2r) = 4.6 ডেসিমি.

∴ অন্তর্ব্যাসার্ধ (r) $=\frac{4.6}{2}=2.3$ ডেসিমি.

ধরি, চোঙটির বহির্ব্যাসের দৈর্ঘ্য 2R ডেসিমি.

প্রশ্নানুযায়ী

$\pi \left ( R^{2}-r^{2} \right )h=84.48$

বা, $\frac{22}{7}\left \{ R^{2}\left ( 2.3 \right )^{2} \right \}\times 28=84.48$

বা, $R^{2}-5.29=\frac{84.48\times 7}{22\times 28}$

বা, $R^{2}=0.96+5.29=6.25$

বা, $R=\sqrt{6.25}$

$\therefore R=2.5$

∴ চোঙটির বহির্ব্যাস = 2.5×2 = 5 ডেসিমি.

উত্তরঃ নির্ণেয় চোঙটির বহির্ব্যাসের দৈর্ঘ্য 5 ডেসিমিটার।

Koshe dekhi 8 class 10

Q15. একটি লম্ববৃত্তাকার চোঙের উচ্চতা উহার ব্যাসার্ধের দ্বিগুণ। যদি উচ্চতা 6 গুণ হতো তবে চোঙটির আয়তন 539 ঘন ডেসিমি. বেশি হতো। চোঙটির উচ্চতা হিসাব করে লিখি।

সমাধানঃ

ধরি, লম্ববৃত্তাকার চোঙের ব্যাসার্ধ r ডেসিমি.।

∴ চোঙটির উচ্চতা (h) = 2r ডেসিমিটার।

∴ বর্তমানে চোঙটির আয়তন $=\pi r^{2}h=\pi r^{2}\left ( 2r \right )=2\pi r^{3}$ ঘন ডেসিমি.

আবার,

যদি উচ্চতা 6 গুণ হতো, অর্থাৎ h = 6×r = 6r ডেসিমি.

∴ এখন চোঙটির আয়তন হবে $=\pi r^{2}h=\pi r^{2}\left ( 6r \right )=6\pi r^{3}$ ঘন ডেসিমি.।

প্রশ্নানুসারে,

$2\pi r^{3}+539=6\pi r^{3}$

বা, $539=6\pi r^{3}-2\pi r^{3}$

বা, $539=4\pi r^{3}$

বা, $539=4\times \frac{22}{7}\times r^{3}$

বা, $\frac{539\times 7}{4\times 22}=r^{3}$

বা, $\frac{49\times 7}{4\times 2}=r^{3}$

বা, $\frac{\left ( 7 \right )^{3}}{\left ( 2 \right )^{3}}=r^{3}$

বা, $\left (\frac{7}{2} \right )^{3}=r^{3}$

$\therefore r=\frac{7}{2}$

$\therefore h=2\times \frac{7}{2}=7$

উত্তরঃ নির্ণেয় চোঙটির উচ্চতা 7 ডেসিমিটার।

Koshe dekhi 8 class 10

Q16. ফায়ার ব্রিগেডের কোনো একটি দল একটি জলভরতি লম্ব বৃত্তাকার ট্যাঙ্কারের জল 2 সেমি. দৈর্ঘ্যের ব্যাসের তিনটি হোস পাইপ দিয়ে মিনিটে 420 মিটার বেগে ঢেলে 40 মিনিটে আগুন নেভাল। যদি ট্যাঙ্কারটির ব্যাসের দৈর্ঘ্য 2.8 মিটার এবং দৈর্ঘ্য 6 মিটার হয়, তবে

(i) আগুন নেভাতে কত জল খরচ হয়েছে এবং

(ii) ট্যাঙ্কারে আর কত জল রয়েছে নির্ণয় করি।

সমাধানঃ

প্রদত্ত,

পাইপের ব্যাস (2r) = 2 সেমি.

$=\frac{2}{10}$ ডেসিমিটার।

∴ পাইপটির ব্যাসার্ধ,

$\left ( r \right )=\frac{2}{10\times 2}=\frac{1}{10}$ ডেসিমিটার।

ট্যাঙ্কারটির ব্যাস (2R)

= 2.8 মিটার

$=\frac{28}{10}$ মিটার

$=\frac{28}{10}\times 10=28$ ডেসিমিটার।

∴ ট্যাঙ্কারটির ব্যাসার্ধ (R)
$=\frac{28}{2}=14$ ডেসিমিটার।

ট্যাঙ্কারটির দৈর্ঘ্য (H)

= 6 মিটার

$=6\times 10=60$ ডেসিমিটার।

ট্যাঙ্কারটিতে যে পরিমান জল ধরে তার আয়তন –

$=\pi R^{2}H$ ঘন ডেসিমিটার।

$=\frac{22}{7}\times \left ( 14 \right )^{2}\times 60$

$=\frac{22\times 14\times 14\times 60}{7}$

$=36960$ ঘন ডেসিমিটার।

$=36960$ লিটার। [ ${\color{Blue} \because }$ 1 ঘন ডেসিমিটার = 1 লিটার ]

জলের পাইপের জলস্তম্ভের দৈর্ঘ্য $\left ( h \right )=420$ মিটার

$=420\times 10=4200$ ডেসিমিটার।

∴ 40 মিনিটে তিনটি হোস পাইপ দিয়ে মোট জল খরচ হয়

$=40\times 3\times \pi r^{2}h$

$=40\times 3\times \frac{22}{7}\times \frac{1}{10}\times 4200$

$=15840$ ঘন ডেসিমি।

$=15840$ লিটার।

ট্যাঙ্কারে বাকি জলের পরিমান $=\left ( 36960-15840 \right )=21120$ লিটার।

উত্তরঃ (i) আগুন নেভাতে 15840 লিটার জল খরচ হয়েছে এবং

(ii) ট্যাঙ্কারে আর 21120 লিটার জল রয়েছে।

Koshe dekhi 8 class 10

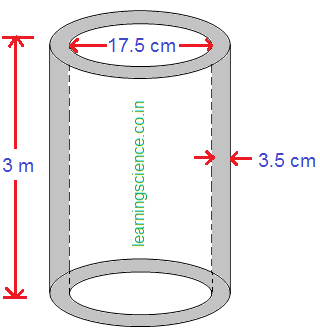
Q17. 17.5 সেমি. ব্যাসের 4টি লম্ব বৃত্তাকার ঢালাই পিলাইয়ের চারিপাশে 3.5 সেমি. পুর বালি-সিমেন্টের প্লাস্টার করতে হবে।

(i) প্রতিটি পিলার যদি 3 মিটার লম্বা হয়, তবে কত ঘন ডেসিমি. মশলা লাগবে হিসাব করে লিখি।

সমাধানঃ

কষে দেখি – 8

প্রদত্ত,

প্রতিটি পিলারের উচ্চতা,

$h=3$ মিটার $=30$ ডেসিমি.

প্রতিটি পিলারের ব্যসের দৈর্ঘ্য,

$2r=17.5$ সেমি.

∴ প্রতিটি পিলারের ব্যাসার্ধের দৈর্ঘ্য,

$r=\frac{17.5}{2}$ সেমি. $=\frac{17.5}{2\times 10}$ ডেসিমি.

$\because$ পিলারগুলো 3.5 সেমি. পুর বালি-সিমেন্টের প্লাস্টার করতে হবে।

∴ প্লাস্টার সহ প্রতিটি পিলারের ব্যাসার্ধর দৈর্ঘ্য,

$R=\left (r+3.5 \right )$ সেমি.

অর্থাৎ, $R=\left ( \frac{17.5}{2}+3.5 \right )$ সেমি.

বা, $R=\left ( 8.75+3.5 \right )=12.25$ সেমি.

$\therefore R=\frac{12.25}{10}$ ডেসিমি.

4 টি পিলার প্লাস্টার করতে যে পরিমান মশলা লাগবে তার আয়তন,

$V=4\times \left ( \pi R^{2}h -\pi r^{2}h\right )$

$=4\pi h\left ( R^{2}-r^{2} \right )$

$=4\pi h\left ( R+r \right )\left ( R-r \right )$

এখন, মান বসিয়ে পাই –

$V=4\times \frac{22}{7}\times 30\times \left ( \frac{12.25}{10}+\frac{17.5}{20} \right )\times \left ( \frac{12.25}{10}-\frac{17.5}{20} \right )$ ঘন ডেসিমি.

$=4\times \frac{22}{7}\times 30\times \left ( 1.225+0.875 \right )\times \left ( 1.225-0.875 \right )$ ঘন ডেসিমি.

$=4\times \frac{22}{7}\times 30\times 2.1\times 0.35$ ঘন ডেসিমি.

$=277.2$ ঘন ডেসিমি. (উত্তর)

(ii) প্লাস্টারের মশলা তৈরি করতে যদি 4 : 1 অনুপাতে বালি ও সিমেন্ট মেশাতে হয়, তবে কত ঘন ডেসিমি. সিমেন্টের প্রয়োজন, হিসাব করে লিখি।

সমাধানঃ

বালি-সিমেন্টের মশলার মোট আয়তন,

$V=277.2$ ঘন ডেসিমি.

$\because$ বালি ও সিমেন্টের আয়তনের অনুপাত = 4 : 1

∴ 277.2 ঘন ডেসিমি. মশলাতে সিমেন্টের পরিমান,

$=\frac{1}{4+1}\times 277.2$ ঘন ডেসিমি.

$=\frac{277.2}{5}$ ঘন ডেসিমি.

$=55.44$ ঘন ডেসিমি. (উত্তর)

Q18. একটি লম্ব বৃত্তাকার ফাপা চোঙের বহিঃর্ব্যাসের দৈর্ঘ্য 16 সেমি. এবং অন্তর্ব্যাসের দৈর্ঘ্য 12 সেমি.। চোঙটির উচ্চতা 36 সেমি.। চোঙটিকে গলিয়ে 2 সেমি. দৈর্ঘ্যের ব্যাসবিশিষ্ট এবং 6 সেমি. দৈর্ঘ্যের কতগুলি নিরেট চোঙ তৈরি করা যাবে হিসাব করি।

সমাধানঃ

কষে দেখি – 8

প্রদত্ত,

$\because$ ফাঁপা চোঙটির বহিঃর্ব্যাসের (2R) ও অন্তর্ব্যাসের (2r) দৈর্ঘ্য যথাক্রমে 16 সেমি. ও 12 সেমি.

∴ ফাঁপা চোঙটির বহিঃব্যাসার্ধ,

$R=\frac{16}{2}=8$ সেমি. এবং

ফাঁপা চোঙটির অন্তর্ব্যাসার্ধ,

$r=\frac{12}{2}=6$ সেমি.

ফাঁপা চোঙটির উচ্চতা,

$h=36$ সেমি.

ফাঁপা চোঙটির উপাদানের আয়তন,

$V_{1}=\pi R^{2}h-\pi r^{2}h$

$\because$ নিরেট চোঙটির ব্যসের দৈর্ঘ্য 2 সেমি.

∴ নিরেট চোঙটির ব্যাসার্ধ,

$R^{'}=\frac{2}{2}=1$ সেমি.

নিরেট চোঙটির উচ্চতা,

$h^{'}=6$ সেমি.

নিরেট চোঙটির উপাদানের আয়তন,

$V_{2}=\pi\left ( R^{'} \right )^{2}h^{'}$

ধরি, একটি ফাঁপা চোঙ গলিয়ে $x$ টি নিরেট চোঙ তৈরী করা যাবে।

∴ $x$ টি নিরেট চোঙের আয়তন = একটি ফাঁপা চোঙের আয়তন

সুতরাং, $x\times V_{2}=V_{1}$

বা, $x\times \pi\times \left ( R^{'} \right )^{2}\times h^{'}=\pi R^{2}h-\pi r^{2}h$

বা, $x\times \pi\times \left ( R^{'} \right )^{2}\times h^{'}=\pi h\left (R^{2}-r^{2} \right )$

বা, $x\times \left ( R^{'} \right )^{2}\times h^{'}=h\left (R^{2}-r^{2} \right )$

বা, $x\times \left ( R^{'} \right )^{2}\times h^{'}=h\left (R+r\right )\left (R-r\right )$

বা, $x=\frac{h\left ( R+r \right )\left ( R-r \right )}{h^{'}\left (R^{'} \right )^{2}}$

এখন মান বসিয়ে পাই –

বা, $x=\frac{36\times \left ( 8+6 \right )\left ( 8-6 \right )}{6\times \left ( 1 \right )^{2}}$

বা, $x=\frac{36\times 14\times 2}{6}$

বা, $x=6\times 14\times 2$

$\therefore x=168$

উত্তরঃ নির্ণেয় 168 টি নিরেট চোঙ তৈরী করা যাবে।

Q19. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A) :

(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) :

(i) দুটি লম্ব বৃত্তাকার নিরেট চোঙের ব্যাসার্ধের দৈর্ঘ্যের অনুপাত 2 : 3 এবং উচ্চতার অনুপাত 5 : 3 হলে, তাদের বক্রতলের ক্ষেত্রফলের অনুপাত

(a) 2 : 5

(b) 8 : 7

(d) 16 : 9

উত্তরঃ (c) 10 : 9

সমাধানঃ

ধরি,

প্রথম লম্ব বৃত্তাকার নিরেট চোঙের ক্ষেত্রে,

ব্যাসার্ধ = 2r একক ও উচ্চতা = 5h একক।

∴ বক্রতলের ক্ষেত্রফল $=2\times \pi \times 2r\times 5h$ $=20\pi rh$ বর্গ একক।

ধরি,

দ্বিতীয় লম্ব বৃত্তাকার নিরেট চোঙের ক্ষেত্রে,

ব্যাসার্ধ = 3r একক ও উচ্চতা = 3h একক।

∴ বক্রতলের ক্ষেত্রফল $=2\times \pi \times 3r\times 3h$ $=18\pi rh$ বর্গ একক।

লম্ব বৃত্তাকার নিরেট চোঙ দুটির বক্রতলের ক্ষেত্রফলের অনুপাত

$=\frac{20\pi rh}{18\pi rh}$

$=\frac{10}{9}$

$=10:9$

Q19. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A) :

(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) :

(ii) দুটি লম্ব বৃত্তাকার নিরেট চোঙের ব্যাসার্ধের দৈর্ঘ্যের অনুপাত 2 : 3 এবং উচ্চতার অনুপাত 5 : 3 হলে, তাদের আয়তনের অনুপাত

(a) 27 : 20

(b) 20 : 27

(d) 9 : 4

উত্তরঃ (b) 20 : 27

সমাধানঃ

ধরি,

প্রথম লম্ব বৃত্তাকার নিরেট চোঙের ক্ষেত্রে,

ব্যাসার্ধ = 2r একক ও উচ্চতা = 5h একক।

∴ আয়তন $=\pi\times \left ( 2r \right )^{2}\times \left ( 5h \right )=20\pi r^{2}h$ ঘন একক।

ধরি,

দ্বিতীয় লম্ব বৃত্তাকার নিরেট চোঙের ক্ষেত্রে,

ব্যাসার্ধ = 3r একক ও উচ্চতা = 3h একক।

∴ আয়তন $=\pi\times \left ( 3r \right )^{2}\times \left ( 3h \right )=27\pi r^{2}h$ ঘন একক।

লম্ব বৃত্তাকার নিরেট চোঙ দুটির আয়তনের অনুপাত

$=\frac{20\pi r^{2}h}{27\pi r^{2}h}$

$=\frac{20}{27}$

$=20:27$

Q19. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A) :

(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) :

(iii) দুটি লম্ব বৃত্তাকার নিরেট চোঙের আয়তন সমান এবং তাদের উচ্চতার অনুপাত 1 : 2 হলে, তাদের ব্যাসার্ধের অনুপাত

(a) ${\color{Blue} 1:\sqrt{2}}$

(b) ${\color{Blue} \sqrt{2}:1}$

(d) 2 : 1

উত্তরঃ (b) ${\color{DarkGreen} \sqrt{2}:1}$

সমাধানঃ

ধরি,

প্রথম লম্ব বৃত্তাকার নিরেট চোঙের ক্ষেত্রে,

ব্যাসার্ধ =r একক ও উচ্চতা = h একক।

∴ আয়তন $=\pi\times \left ( r \right )^{2}\times h=\pi r^{2}h$ ঘন একক।

ধরি,

দ্বিতীয় লম্ব বৃত্তাকার নিরেট চোঙের ক্ষেত্রে,

ব্যাসার্ধ = R একক ও উচ্চতা = 2h একক।

∴ আয়তন $=\pi\times \left ( R \right )^{2}\times \left ( 2h \right )=2\pi R^{2}h$ $=\pi\times \left ( R \right )^{2}\times \left ( 2h \right )=2\pi R^{2}h$ ঘন একক।

প্রশ্নানুসারে,

প্রথম লম্ব বৃত্তাকার নিরেট চোঙের আয়তন = দ্বিতীয় লম্ব বৃত্তাকার নিরেট চোঙের আয়তন

$\pi r^{2}h=2\pi R^{2}h$

বা, $r^{2}=2R^{2}$

বা, $\frac{r^{2}}{R^{2}}=\frac{2}{1}$

বা, $\frac{r}{R}=\sqrt{\frac{2}{1}}$

$\therefore r:R=\sqrt{2}:1$

Q19. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A) :

(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) :

(iv) একটি লম্ব বৃত্তাকার চোঙের ব্যাসার্ধের দৈর্ঘ্য অর্ধেক এবং উচ্চতা দ্বিগুণ হলে, চোঙটির আয়তন হবে পূর্বের চোঙের আয়তনের

(a) সমান

(b) দ্বিগুণ

(d) 4 গুণ

উত্তরঃ (c) অর্ধেক

সমাধানঃ

ধরি,

পূর্বের লম্ব বৃত্তাকার চোঙের ক্ষেত্রে,

ব্যাসার্ধ = r একক ও উচ্চতা = h একক।

∴ আয়তন $=\pi r^{2}h$ ঘন একক।

ধরি,

বর্তমান লম্ব বৃত্তাকার চোঙের ক্ষেত্রে,

ব্যাসার্ধ $=\frac{r}{2}$ একক ও উচ্চতা = 2h একক।

∴ আয়তন $=\pi \times \left ( \frac{r}{2} \right )^{2}\times 2h=\frac{\pi r^{2}h}{2}$ ঘন একক।

বর্তমান লম্ব বৃত্তাকার চোঙের আয়তন $=\frac{1}{2}\times \pi r^{2}h$ ঘন একক।

$=\frac{1}{2}\times$ পূর্বের লম্ব বৃত্তাকার চোঙের আয়তন।

Q19. অতিসংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (V.S.A) :

(A) বহুবিকল্পীয় প্রশ্ন (M.C.Q.) :

(v) একটি লম্ব বৃত্তাকার চোঙের ব্যাসার্ধের দৈর্ঘ্য দ্বিগুণ এবং উচ্চতা অর্ধেক করা হলে, বক্রতলের ক্ষেত্রফল পূর্বের চোঙের বক্রতলের ক্ষেত্রফলের

(a) সমান

(b) দ্বিগুণ

(d) 4 গুণ

উত্তরঃ (a) সমান

সমাধানঃ

ধরি,

পূর্বের লম্ব বৃত্তাকার চোঙের ক্ষেত্রে,

ব্যাসার্ধ = r একক ও উচ্চতা = h একক।

∴ বক্রতলের ক্ষেত্রফল $=2\times \pi \times r\times h=2\pi rh$ বর্গ একক।

ধরি,

বর্তমান লম্ব বৃত্তাকার চোঙের ক্ষেত্রে,

ব্যাসার্ধ $=2r$ একক ও উচ্চতা $=\frac{h}{2}$ একক।

∴ বক্রতলের ক্ষেত্রফল $=2\times \pi \times 2r\times \frac{h}{2}=2\pi rh$ বর্গ একক।

∴ বর্তমান লম্ব বৃত্তাকার চোঙের বক্রতলের ক্ষেত্রফল = পূর্বের লম্ব বৃত্তাকার চোঙের বক্রতলের ক্ষেত্রফল।

19 (B) নীচের বিবৃতিগুলি সত্য না মিথ্যা লিখি :

(i) একটি লম্ব বৃত্তাকার চোঙাকৃতি ড্রামের ব্যাসার্ধের দৈর্ঘ্য r সেমি. এবং উচ্চতা h সেমি.। ড্রামের অর্ধেক জলপূর্ণ থাকলে, জলের আয়তন হবে ${\color{Blue} \pi r^{2}h}$ ঘন সেমি.।

উত্তরঃ বিবৃতিটি মিথ্যা।

ব্যাখ্যা :

প্রদত্ত,

লম্ব বৃত্তাকার চোঙাকৃতি ড্রামের ব্যাসার্ধের দৈর্ঘ্য r সেমি. এবং উচ্চতা h সেমি.।

∴ সম্পূর্ণ ড্রামের আয়তন $=\pi r^{2}h$ ঘন একক।

ড্রামটিতে অর্ধেক জলপূর্ণ থাকলে, জলের আয়তন হবে $=\frac{1}{2}\times \pi r^{2}h$ ঘন একক।

(ii) একটি লম্ব বৃত্তাকার চোঙের ব্যাসার্ধের দৈর্ঘ্য 2 একক হলে, চোঙটির যে-কোনো উচ্চতার জন্য চোঙটির আয়তন এবং বক্রতলের ক্ষেত্রফলের সাংখ্যমান সমান হবে।

উত্তরঃ বিবৃতিটি সত্য।

ব্যাখ্যা :

প্রদত্ত,

লম্ব বৃত্তাকার চোঙের ব্যাসার্ধের দৈর্ঘ্য 2 একক।

ধরি, চোঙটির উচ্চতা h একক।

∴ চোঙটির আয়তন $=\pi \left ( 2 \right )^{2}h=4\pi h$ ঘন একক ও

বক্রতলের ক্ষেত্রফল $=2\pi \times 2\times h=4\pi h$ বর্গ একক।

19 (C) শূন্যস্থান পূরণ করি :

(i) একটি আয়তক্ষেত্রাকার কাগজের দৈর্ঘ্য ${\color{Blue} l}$ একক এবং প্রস্থ b একক। আয়তক্ষেত্রকার কাগজটি মুড়ে একটি লম্ব বৃত্তাকার চোঙ তৈরি করা হলো যার পরিধি কাগজটির দৈর্ঘ্যের সমান। চোঙটির বক্রতলের ক্ষেত্রফল _______ বর্গ একক।

সমাধানঃ

একটি আয়তক্ষেত্রাকার কাগজের দৈর্ঘ্য ${\color{Blue} l}$ একক এবং প্রস্থ b একক। আয়তক্ষেত্রকার কাগজটি মুড়ে একটি লম্ব বৃত্তাকার চোঙ তৈরি করা হলো যার পরিধি কাগজটির দৈর্ঘ্যের সমান। চোঙটির বক্রতলের ক্ষেত্রফল lb বর্গ একক।

[ Note : চোঙের বক্রতলের ক্ষেত্রফল = (2πr) × h

যেখানে,

l = 2πr = চোঙের বৃত্তাকার তলের পরিধি।

b = h = চোঙের উচ্চতা ]

(ii) একটি লম্ব বৃত্তাকার চোঙের ব্যাসের দৈর্ঘ্য 3 সেমি. এবং উচ্চতা 4 সেমি. হলে, চোঙটির ভিতর সর্বাপেক্ষা লম্বা যে দন্ড রাখা যাবে তার দৈর্ঘ্য ____ সেমি.।

সমাধানঃ

একটি লম্ব বৃত্তাকার চোঙের ব্যাসের দৈর্ঘ্য 3 সেমি. এবং উচ্চতা 4 সেমি. হলে, চোঙটির ভিতর সর্বাপেক্ষা লম্বা যে দন্ড রাখা যাবে তার দৈর্ঘ্য 5 সেমি.।

ব্যাখ্যা :

প্রদত্ত,

লম্ব বৃত্তাকার চোঙের ব্যাসের দৈর্ঘ্য 3 সেমি. এবং উচ্চতা 4 সেমি.

∴ চোঙটির ভিতর সর্বাপেক্ষা লম্বা যে দন্ড রাখা যাবে তার দৈর্ঘ্য হবে $=\sqrt{\left ( 3 \right )^{2}+\left ( 4 \right )^{2}}=\sqrt{9+16}=\sqrt{25}=5$ সেমি।

(iii) একটি লম্ব বৃত্তাকার চোঙের আয়তন এবং বক্রতলের ক্ষেত্রফলের সাংখ্যমান সমান হলে, চোঙটির ব্যাসের দৈর্ঘ্য _______ একক।

সমাধানঃ

একটি লম্ব বৃত্তাকার চোঙের আয়তন এবং বক্রতলের ক্ষেত্রফলের সাংখ্যমান সমান হলে, চোঙটির ব্যাসের দৈর্ঘ্য 4 একক।

ব্যাখ্যা :

ধরি, লম্ব বৃত্তাকার চোঙের ব্যাসার্ধ r একক ও উচ্চতা h একক।

∴ চোঙটির আয়তন $=\pi r^{2}h$ ঘন একক ও বক্রতলের ক্ষেত্রফল $=2\pi rh$ বর্গ একক।

প্রশ্নানুযায়ী,

$\pi r^{2}h=2\pi rh$

বা, $r=2$

∴ব্যাস $=2r=2\times 2=4$ একক।

Q20. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) :

(i) একটি লম্ব বৃত্তাকার চোঙাকৃতি স্তম্ভের বক্রতলের ক্ষেত্রফল 264 বর্গ মিটার এবং আয়তন 924 ঘন মিটার হলে, স্তম্ভের ভূমির ব্যাসার্ধের দৈর্ঘ্য কত লিখি।

সমাধানঃ

ধরি, লম্ব বৃত্তাকার চোঙাকৃতি স্তম্ভের ব্যাসার্ধ r মিটার ও উচ্চতা h মিটার।

প্রদত্ত,

স্তম্ভের বক্রতলের ক্ষেত্রফল 264 বর্গ মিটার এবং আয়তন 924 ঘন মিটার।

$\therefore 2\pi rh=264$

বা, $\pi rh=\frac{264}{2}=132$ ……..(i)

আবার,

$\pi r^{2}h=924$

বা, $\pi rh\times r=924$

বা, $132r=924$

∴ $r=\frac{924}{132}=7$

উত্তরঃ নির্ণেয় স্তম্ভের ভূমির ব্যাসার্ধের দৈর্ঘ্য 7 মিটার।

Q20. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) :

(ii) একটি লম্ব বৃত্তাকার চোঙের বক্রতলের ক্ষেত্রফল c বর্গ একক, ভূমির ব্যাসার্ধের দৈর্ঘ্য r একক এবং আয়তন v ঘন একক হলে, ${\color{Blue} \frac{cr}{v}}$ এর মান কত তা লিখি।

সমাধানঃ

ধরি, লম্ব বৃত্তাকার চোঙের উচ্চতা h একক।

প্রদত্ত,

চোঙের ব্যাসার্ধ r একক, আয়তন $\pi r^{2}h=v$ ঘন একক এবং

বক্রতলের ক্ষেত্রফল $2\pi rh=c$ বর্গ একক।

$\therefore \frac{cr}{v}$ এর মান হবে

$=\frac{2\pi rh\times r}{\pi r^{2}h}$

$=2$

উত্তরঃ নির্ণেয় ${\color{DarkGreen} \frac{cr}{v}}$ এর মান 2

Q20. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) :

(iii) একটি লম্ব বৃত্তাকার চোঙের উচ্চতা 14 সেমি. এবং বক্রতলের ক্ষেত্রফল 264 বর্গ সেমি. হলে, চোঙটির আয়তন কত তা লিখি।

সমাধানঃ

ধরি, লম্ব বৃত্তাকার চোঙের ব্যাসার্ধ r সেমি.।

প্রদত্ত,

চোঙের উচ্চতা (h)= 14 সেমি., এবং

বক্রতলের ক্ষেত্রফল 264 বর্গ সেমি.।

অর্থাৎ,

$2\pi rh=264$

বা, $2\times \frac{22}{7}\times r\times 14=264$

বা, $r=\frac{264\times 7}{2\times 22\times 14}$

$\therefore r=3$

∴ চোঙটির আয়তন

$=\pi r^{2}h$

$=\frac{22}{7}\times \left ( 3 \right )^{2}\times 14$

$=22\times 9\times 2$

$=396$ ঘন সেমি।

উত্তরঃ নির্ণেয় চোঙটির আয়তন 396 ঘন সেমি।

Q20. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) :

(iv) দুটি লম্ব বৃত্তাকার চোঙের উচ্চতার অনুপাত 1 : 2 এবং ভূমির পরিধির অনুপাত 3 : 4 হলে, তাদের আয়তনের অনুপাত কত তা লিখি।

সমাধানঃ

ধরি,

প্রথম লম্ব বৃত্তাকার চোঙের ক্ষেত্রে,

ব্যাসার্ধ = r একক ও উচ্চতা = h একক।

∴ ভূমির পরিধি $=2\pi r$ একক ও আয়তন $=\pi r^{2}h$ ঘন একক।

ধরি,

দ্বিতীয় লম্ব বৃত্তাকার চোঙের ক্ষেত্রে,

ব্যাসার্ধ = R একক ও উচ্চতা = 2h একক।

∴ ভূমির পরিধি $=2\pi R$ একক ও আয়তন $\pi\times R^{2}\times 2h=2\pi R^{2}h$ ঘন একক।

প্রশ্নানুযায়ী,

$\frac{2\pi r}{2\pi R}=\frac{3}{4}$

বা, $\frac{r}{R}=\frac{3}{4}$

লম্ব বৃত্তাকার নিরেট চোঙ দুটির আয়তনের অনুপাত

$=\frac{\pi r^{2}h}{2\pi R^{2}h}$

$=\frac{1}{2}\times \left ( \frac{r}{R} \right )^{2}$

$=\frac{1}{2}\times \left ( \frac{3}{4} \right )^{2}$

$=\frac{1}{2}\times \frac{3}{4}\times \frac{3}{4}$

$=\frac{9}{32}$

$=9:32$

উত্তরঃ নির্ণেয় লম্ব বৃত্তাকার নিরেট চোঙ দুটির আয়তনের অনুপাত 9 : 32

Q20. সংক্ষিপ্ত উত্তরধর্মী প্রশ্ন (S.A.) :

(v) একটি লম্ব বৃত্তাকার চোঙের ব্যাসার্ধের দৈর্ঘ্য 50% হ্রাস করা হলো এবং উচ্চতা 50% বৃদ্ধি করা হলো। চোঙর্টির আয়তনের শতকরা কত পরিবর্তন হবে তা লিখি।

সমাধানঃ

ধরি, লম্ব বৃত্তাকার চোঙের ব্যাসার্ধ r একক এবং উচ্চতা h একক।

∴ চোঙর্টির আয়তন $=\pi r^{2}h$ ঘন একক।

ব্যাসার্ধ 50% হ্রাস পেলে এখন ব্যাসার্ধ হবে

$=r-r\times \frac{50}{100}$

$=r-r\times \frac{1}{2}$

$=\frac{r}{2}$ একক।

উচ্চতা 50% বৃদ্ধি পেলে বর্তমান উচ্চতা হবে

$=h+h\times \frac{50}{100}$

$=h+\frac{h}{2}$

$=\frac{3h}{2}$ একক।

∴ চোঙর্টির বর্তমান আয়তন

$=\pi \times \left ( \frac{r}{2} \right )^{2}\times \frac{3h}{2}$

$=\frac{3\pi r^{2}h}{8}$ ঘন একক।

চোঙর্টির আয়তন হ্রাস পায়

$=\pi r^{2}h-\frac{3\pi r^{2}h}{8}$

$=\frac{8\pi r^{2}h-3\pi r^{2}h}{8}$

$=\frac{5\pi r^{2}h}{8}$ ঘন একক।

∴ চোঙর্টির আয়তন হ্রাসের শতকরা হার

$=\frac{\frac{5\pi r^{2}h}{8}}{\pi r^{2}h}\times 100%$

$=\frac{5\pi r^{2}h}{8}\times \frac{1}{\pi r^{2}h}\times 100%$

$=\frac{5}{8}\times 100%$

$=\frac{125}{2}%$

$=62\frac{1}{2}%$

উত্তরঃ নির্ণেয় চোঙর্টির আয়তনের শতকরা ${\color{DarkGreen} 62\frac{1}{2}}{\color{DarkGreen} %}$ পরিবর্তন হবে।