Madhyamik 2022 Math Paper Solution

1. নিম্নলিখিত প্রশ্নগুলির প্রতিটি ক্ষেত্রে সঠিক উত্তরটি নির্বাচন করাে। (1 × 6 = 6)

(i) একটি গ্রামের জনসংখ্যা p এবং প্রতি বছর জনসংখ্যা বৃদ্ধির হাঁর 2r % হলে, n বছর পর জনসংখ্যা হবে

(a) $p\left ( 1+\frac{r}{100} \right )^{n}$

(b) $p\left ( 1+\frac{r}{50} \right )^{n}$

(d) $p\left ( 1-\frac{r}{100} \right )^{n}$

সমাধানঃ আমরা জানি, গ্রামের বর্তমান জনসংখ্যা p এবং প্রতি বছর জনসংখ্যা বৃদ্ধির হাঁর 2r % হলে,

n বছর পর জনসংখ্যা হবে

$=p\left ( 1+\frac{2r}{100} \right )^{n}$

$= p\left ( 1+\frac{r}{50} \right )^{n}$

উত্তরঃ (b) ${\color{DarkGreen} p\left ( 1+\frac{r}{50} \right )^{n}}$

(ii) ফতিমা, শ্রেয়া এবং স্মিতা তিনজনে মােট 6,000 টাকা দিয়ে একটি ব্যবসা শুরু করে। এক বছর পরে ফতিমা, শ্রেয়া এবং স্মিতা যথাক্রমে লভ্যাংশের 50 টাকা, 100 টাকা এবং 150 টাকা পায়। স্মিতা ঐ ব্যবসায় নিয়ােজিত করে :

(a) 1,000 টাকা

(b) 2,000 টাকা

(d) 4,000 টাকা

সমাধানঃ

প্রশ্নানুযায়ী, গাণিতিক সমস্যাটি সরল অংশীদারী কারবার।

∴ মূলধনের অনুপাত = লভ্যাংশের অনুপাত

সুতরাং, ফতিমা, শ্রেয়া এবং স্মিতার মূলধনের অনুপাত

= 50 : 100 : 150

= 5 : 10 : 15

= 1 : 2 : 3

স্মিতার মূলধনের আনুপাতিক ভাগহার $=\frac{3}{1+2+3}=\frac{3}{6}=\frac{1}{2}$

∴ স্মিতা ব্যবসায় নিয়োজিত করে $=6000\times \frac{1}{2}=3000$ টাকা।

উত্তরঃ (c) 3,000 টাকা

(iii) A : B = 2 : 3, B : C = 5 : 8, C : D = 6 : 7 হলে , A : D = কত ?

(a) 2 : 7

(b) 7 : 2

(d) 5 : 14

সমাধানঃ

A : B = 2 : 3

বা, $\frac{A}{B}=\frac{2}{3}$

B : C = 5 : 8

বা, $\frac{B}{C}=\frac{5}{8}$

এবং

C : D = 6 : 7

বা, $\frac{C}{D}=\frac{6}{7}$

$\therefore \frac{A}{D}=\frac{A}{B}\times \frac{B}{C}\times \frac{C}{D}=\frac{2}{3}\times \frac{5}{8}\times \frac{6}{7}=\frac{5}{14}$

উত্তরঃ (d) 5 : 14

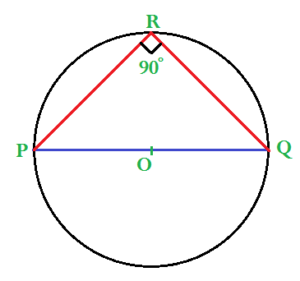
(iv) ‘O’ কেন্দ্রীয় বৃত্তে PQ একটি ব্যাস; R বৃত্তের ওপর একটি বিন্দু এবং PR = RQ হলে ∠RPQ এর মান :

(a) 30°

(b) 90°

(d) 45°

সমাধানঃ (d) 45°

madhyamik 2022 math paper solution

যেহেতু, ΔPQR -এর PQ হলো বৃত্তটির ব্যাস।

∴ ∠PRQ = 90° [অর্ধবৃত্তস্থ কোণ]

আবার, ΔPQR -এর PR = PQ [প্রদত্ত]

∴ ΔPQR হলো সমকোণী সমদ্বিবাহু ত্রিভুজ যার।

সুতরাং, ∠RPQ = 45° ….. (d)

(v) দুটি বৃত্ত পরস্পরকে স্পর্শ বা ছেদ না করলে বৃত্তদুটির সাধারণ স্পর্শক সংখ্যা :

(a) 2 টি

(b) 1 টি

(d) 4 টি

সমাধানঃ

উত্তরঃ (d) 4 টি

মাধ্যমিক ২০২২ গণিত প্রশ্নপত্র

(vi) 2r একক দৈর্ঘ্যের ব্যাসার্ধবিশিষ্ট নিরেট গােলকের আয়তন :

(a) $\frac{32\pi r^{3}}{3}$ ঘন একক

(b) $\frac{16\pi r^{3}}{3}$ ঘন একক

(d) $\frac{64\pi r^{3}}{3}$ ঘন একক

সমাধানঃ

2r একক দৈর্ঘ্যের ব্যাসার্ধবিশিষ্ট নিরেট গােলকের আয়তন

$=\frac{4}{3}\pi \left ( 2r \right )^{3}$ ঘনএকক

$=\frac{32\pi r^{3}}{3}$ ঘনএকক

উত্তরঃ (a) ${\color{DarkGreen} \frac{32\pi r^{3}}{3}}$ ঘনএকক

2. শূন্যস্থান পূরণ করাে (যে কোনাে পাঁচটি) : 1 × 5 = 5

(i) বার্ষিক চক্রবৃদ্ধি সুদের হার r% এবং প্রথম বছরের মূলধন P টাকা হলে, দ্বিতীয় বছরের মূলধন ____।

সমাধানঃ

দ্বিতীয় বছরের মূলধন

= প্রথম বছরের মূলধন + প্রথম বছরের সরল সুদ

$=p+\frac{pr\times 1}{100}$ [ যেখানে, সময়(t) = 1 ]

${\color{DarkGreen} =p\left (1+\frac{r}{100} \right )}$ (উত্তর)

2. শূন্যস্থান পূরণ করাে (যে কোনাে পাঁচটি) : 1 × 5 = 5

(ii) $7\sqrt{11}$ একটি ___ সংখ্যা।

উত্তরঃ

$7\sqrt{11}$ একটি অমূলদ সংখ্যা।

2. শূন্যস্থান পূরণ করাে (যে কোনাে পাঁচটি) : 1 × 5 = 5

(iii) কোনাে গােলকের ব্যাসার্ধ r এবং আয়তন v হলে, v ∝ ____ ।

সমাধানঃ

গােলকের আয়তন

$v=\frac{4}{3}\pi r^{3}$

∴ v ∝ r³ (উত্তর)

2. শূন্যস্থান পূরণ করাে (যে কোনাে পাঁচটি) : 1 × 5 = 5

(iv) দুটি ত্রিভুজ সদৃশ হবে, যদি তাদের অনুরুপ বাহুগুলি _____ হয়।

সমাধানঃ সমানুপাতী

madhyamik 2022 math paper solution

2. শূন্যস্থান পূরণ করাে (যে কোনাে পাঁচটি) : 1 × 5 = 5

(v) একটি চতুর্ভুজের বিপরীত কোণদ্বয় পরস্পর সম্পূরক হলে, চতুর্ভুজের শীর্ষবিন্দুগুলি ________।

সমাধানঃ সমবৃত্তস্থ (গণিত প্রকাশ দশম শ্রেণী বইটির পৃষ্ঠা নম্বর 165)

madhyamik 2022 math paper solution

2. শূন্যস্থান পূরণ করাে (যে কোনাে পাঁচটি) : 1 × 5 = 5

(vi) সমকোণী চৌপলের দৈর্ঘ্য, প্রস্থ ও উচ্চতা সমান হলে সেই ঘনবস্তুর বিশেষ নাম ______।

উত্তরঃ ঘনক

Madhyamik 2022 Math Paper Solution

Madhyamik 2020 Math Paper Solution

Madhyamik 2019 Math Paper Solution

Madhyamik 2018 Math Paper Solution

Madhyamik 2017 Math Paper Solution

3. সত্য বা মিথ্যা লেখাে (যে কোনাে পাঁচটি) : 1 × 5=5

(i) অংশীদারি ব্যবসায় কমপক্ষে 3 জন লােকের দরকার।

উত্তরঃ মিথ্যা

3. সত্য বা মিথ্যা লেখাে (যে কোনাে পাঁচটি) : 1 × 5=5

(ii) আসল ও সবৃদ্ধিমূলের মধ্যে সম্পর্কটি হল আসল < সবৃদ্ধিমূল।

উত্তরঃ সত্য

3. সত্য বা মিথ্যা লেখাে (যে কোনাে পাঁচটি) : 1 × 5=5

(iii) x² = 100 সমীকরণের দুটি বীজ হল ± 10.

উত্তরঃ সত্য

3. সত্য বা মিথ্যা লেখাে (যে কোনাে পাঁচটি) : 1 × 5=5

(iv) a ও b ব্যস্ত ভেদে থাকলে, $\frac{a}{b}$ = ধ্রুবক হবে।

উত্তরঃ মিথ্যা

3. সত্য বা মিথ্যা লেখাে (যে কোনাে পাঁচটি) : 1 × 5=5

(v) দুটি এককেন্দ্রীয় বৃত্তের একটি মাত্র সাধারণ স্পর্শক থাকবে।

উত্তরঃ বিবৃতিটি মিথ্যা

ব্যাখ্যা : দুটি এককেন্দ্রীয় বৃত্তের কোনো সাধারণ স্পর্শক থাকা সম্ভব নয়।

3. সত্য বা মিথ্যা লেখাে (যে কোনাে পাঁচটি) : 1 × 5=5

(vi) একটি লম্ব বৃত্তাকার শঙ্কুর উচ্চতা, ব্যাসার্ধ এবং তির্যক উচ্চতা সর্বদা একটি সমকোণী ত্রিভুজের বাহুত্রয়।

উত্তরঃ সত্য

4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাওঃ (যে কোনাে দশটি) 2 × 10 = 20

(i) বার্ষিক সুদ আসলের $\frac{1}{16}$ অংশ হলে, 8 মাসে 690 টাকার সুদ কত হবে ?

সমাধানঃ

ধরি,

আসল (p) = 16x টাকা, বার্ষিক সুদ (I) = x টাকা ও বার্ষিক সুদের হার = r %

প্রদত্ত,

সময় (t) = 12 মাস [ যেহেতু, 12 মাস = 1 বছর ]

আমরা জানি,

$I=\frac{prt}{100}$

বা, $x=\frac{16x\times r\times 12}{100}$

বা, $r=\frac{100}{16\times 12}$

$\therefore r=\frac{25}{48}$

আবার,

আসল (p) = 690 টাকা,

সময় (t) = 8 মাস

ও বার্ষিক সুদের হার $\left (r \right )=\frac{25}{48}%$

সুতরাং, 8 মাসে 690 টাকার সুদ

$I=\frac{690\times 25\times 8}{48\times 100}$

বা, $I=\frac{115}{4}$

∴ I = 28.75

উত্তরঃ নির্ণেয় সুদের পরিমান 28.75 টাকা।

4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাওঃ (যে কোনাে দশটি) 2 × 10 = 20

(ii) কোনাে স্থানের লােকসংখ্যা 13,310 জন ছিল। কি হারে বৃদ্ধি পেলে 3 বছরে 17,280 জন হবে ?

সমাধানঃ

ধরি, লােকসংখ্যা বৃদ্ধির হার = r %

প্রদত্ত,

A = 17280 জন, p = 13310 জন ও t = 3 বছর

আমরা জানি,

$A=p\left ( 1+\frac{r}{100} \right )^{t}$

বা, $17280=13310\left ( 1+\frac{r}{100} \right )^{3}$

বা, $\frac{17280}{13310}=\left ( 1+\frac{r}{100} \right )^{3}$

বা, $\frac{1728}{1331}=\left ( 1+\frac{r}{100} \right )^{3}$

বা, $\left (\frac{12}{11} \right )^{3}=\left ( 1+\frac{r}{100} \right )^{3}$

বা, $\frac{12}{11}=1+\frac{r}{100}$

বা, $\frac{12}{11}-1=\frac{r}{100}$

বা, $\frac{1}{11}=\frac{r}{100}$

বা, $r=\frac{100}{11}$

$\therefore r=9\frac{1}{11}%$

উত্তরঃ নির্ণেয় সুদের হার ${\color{DarkGreen} 9\frac{1}{11}%}$

Madhyamik 2022 Math Paper Solution

4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাওঃ (যে কোনাে দশটি) 2 × 10 = 20

(iii) কোনাে ব্যবসাতে A, B, C এর মূলধনের অনুপাত $\frac{1}{x}:\frac{1}{y}:\frac{1}{z}$ , বছরের শেষে ব্যবসাতে z টাকা ক্ষতি হয়েছে। C -এর ক্ষতির পরিমাণ নির্ণয় করাে।

সমাধানঃ

C এর মূলধনের আনুপাতিক ভাগহার

$=\frac{\frac{1}{z}}{\frac{1}{x}+\frac{1}{y}+\frac{1}{z}}$

$=\frac{\frac{1}{z}}{\frac{yz+xz+xy}{xyz}}$

$= \frac{1}{z}\times \frac{xyz}{yz+xz+xy}$

$= \frac{xy}{yz+xz+xy}$

বছরের শেষে ব্যবসায় z টাকা ক্ষতি হলে,

C -এর ক্ষতির পরিমাণ

$= z\times \frac{xy}{yz+xz+xy}$

$= \frac{xyz}{yz+xz+xy}$ টাকা।

উত্তরঃ নির্ণেয় C -এর ক্ষতির পরিমাণ ${\color{DarkGreen} \frac{xyz}{yz+xz+xy}}$ টাকা।

Madhyamik 2022 Math Paper Solution

4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাওঃ (যে কোনাে দশটি) 2 × 10 = 20

(iv) 7x² − 66x + 27 = 0 সমীকরণটির বীজদ্বয়ের যােগফল ও গুণফলের অনুপাত কতাে ?

সমাধানঃ

7x² − 66x + 27 = 0 সমীকরণটিকে $ax^{2}+bx+c=0$ সমীকরণের সাথে তুলনা করে পাই,

a = 7, b = − 66, c = 27

ধরি, 7x² − 66x + 27 = 0 সমীকরণটির বীজদ্বয় α ও β

আমরা জানি,

বীজদ্বয়ের যােগফল = α + β $=-\frac{b}{a}=-\frac{-66}{7}=\frac{66}{7}$

ও গুণফল = αβ $=\frac{c}{a}=\frac{27}{7}$

∴ প্রদত্ত সমীকরণটির বীজদ্বয়ের যােগফল ও গুণফলের অনুপাত

$=\frac{66}{7}:\frac{27}{7}$

$=\frac{66}{7}\times 7:\frac{27}{7}\times 7$

= 66 : 27

= 22 : 9 (উত্তর)

Madhyamik 2022 Math Paper Solution

4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাওঃ (যে কোনাে দশটি) 2 × 10 = 20

(v) হরের করণী নিরসন করাে : $\frac{12}{\sqrt{15}-3}$

সমাধানঃ

$\frac{12}{\sqrt{15}-3}$

হরের করণী নিরসন করে পাই,

$=\frac{12\left (\sqrt{15}+3 \right )}{\left (\sqrt{15}-3 \right )\left (\sqrt{15}+3 \right )}$

$=\frac{12\left (\sqrt{15}+3 \right )}{\left (\sqrt{15} \right )^{2}-\left (3 \right )^{2}}$ ${\color{Blue} \left [\because \left ( a+b \right )\left ( a-b \right )=a^{2}-b^{2} \right ]}$

$=\frac{12\left (\sqrt{15}+3 \right )}{15-9}$

$=\frac{12\left (\sqrt{15}+3 \right )}{6}$

${\color{DarkGreen} =2\left (\sqrt{15}+3 \right )}$ (উত্তর)

Madhyamik 2022 Math Paper Solution

4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাওঃ (যে কোনাে দশটি) 2 × 10 = 20

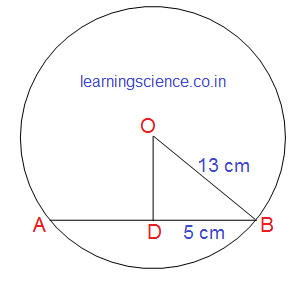
(vi) ‘O’ কেন্দ্রীয় একটি বৃত্তের ব্যাসার্ধের দৈর্ঘ্য 13 সেমি. এবং AB একটি জ্যা এর দৈর্ঘ্য 10 সেমি., ‘O’ বিন্দু থেকে AB জ্যা এর দূরত্ব কত ?

সমাধানঃ

কষে দেখি – 3.2

madhyamik 2022 math paper solution

Madhyamik 2022 Math Paper Solution

4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাওঃ (যে কোনাে দশটি) 2 × 10 = 20

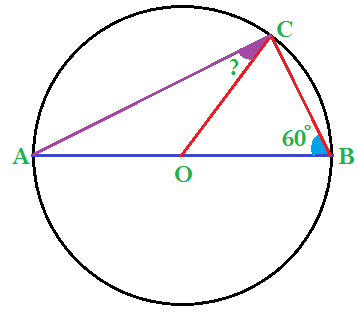
(vii) AOB বৃত্তের একটি ব্যাস যার কেন্দ্র O, C বৃত্তের উপর একটি বিন্দু। ∠OBC = 60°, হলে ∠OCA -এর মান নির্ণয় করাে।

সমাধানঃ

madhyamik 2022 math paper solution

ΔOBC -এর OB = OC [একই বৃত্তের ব্যাসার্ধ]

∴ ∠OCB = ∠OBC [ত্রিভুজের সমান বাহু দুটির বিপরীত কোণ দুটি সমান হয়]

অর্থাৎ, ∠OCB = 60° [যেহেতু, ∠OBC = 60°]

আবার, যেহেতু AOB হলো বৃত্তটির ব্যাস এবং C বৃত্তটির উপরিস্থ যেকোনো একটি বিন্দু।

∴ ∠ACB = 90° [অর্ধবৃত্তস্থ কোণ]

এখন, ∠OCA = ∠ACB − ∠OCB

বা, ∠OCA = 90° − 60°

∴ ∠OCA = 30° (উত্তর)

Madhyamik 2022 Math Paper Solution

4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাওঃ (যে কোনাে দশটি) 2 × 10 = 20

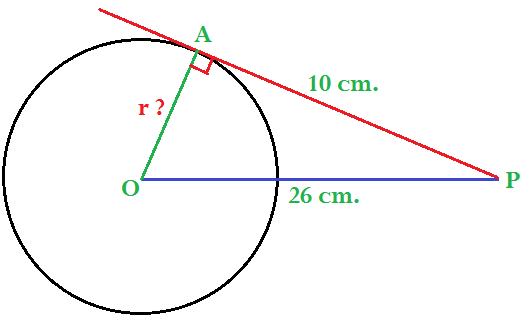
(viii) একটি ‘O’ কেন্দ্রীয় বৃত্ত যার কেন্দ্র থেকে 26 সেমি. দূরত্বে অবস্থিত P বিন্দু থেকে অতি বৃত্তের স্পর্শকের দৈর্ঘ্য 10 সেমি. হলে, বৃত্তের ব্যাসার্ধের দৈর্ঘ্য কত ?

সমাধানঃ

madhyamik 2022 math paper solution

r = OA = O কেন্দ্রীয় বৃত্তের ব্যাসার্ধ।

যেহেতু, O কেন্দ্রীয় বৃত্তের AP হলো স্পর্শক এবং OA হলো স্পর্শবিন্দুগামী ব্যাসার্ধ।

OA ⊥ AP অর্থাৎ, ΔOAP হলো সমকোণী ত্রিভুজ যার OP হলো অতিভুজ।

এখন, পিথাগোরাসের সূত্র থেকে আমরা বলতে পারি যে,

$OA=\sqrt{\left (OP \right )^{2}-\left ( AP \right )^{2}}$

বা, $OA=\sqrt{26^{2}-10^{2}}$

বা, $OA=\sqrt{676-100}$

বা, $OA=\sqrt{576}$

∴ $OA=24 \; cm.$ (উত্তর)

Madhyamik 2022 Math Paper Solution

4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাওঃ (যে কোনাে দশটি) 2 × 10 = 20

(ix) ΔABC -এর DE || BC, যেখানে D ও E যথাক্রমে AB ও AC বাহুর ওপর অবস্থিত। যদি AD = 5 সেমি., DB = 6 সেমি. এবং AE = 7.5 সেমি. হয়, তবে AC এর দৈর্ঘ্য নির্ণয় করাে।

সমাধানঃ

madhyamik 2022 math paper solution

যেহেতু, DE || BC

∴ $\frac{AC}{AE}=\frac{AB}{AD}$ [থ্যালেসের উপপাদ্য অনুসারে]

বা, $\frac{AC}{AE}=\frac{AD+BD}{AD}$

বা, $\frac{AC}{7.5}=\frac{5+6}{5}$

বা, $\frac{AC}{7.5}=\frac{11}{5}$

বা, $AC=\frac{11\times 7.5}{5}=11\times 1.5=16.5$

∴ AC = 16.5 cm. (উত্তর)

Madhyamik 2022 Math Paper Solution

4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাওঃ (যে কোনাে দশটি) 2 × 10 = 20

(x) দুটি লম্ববৃত্তাকার চোঙের উচ্চতার অনুপাত 1 : 2, ভূমির পরিধির অনুপাত 3 : 4 হলে, তাদের আয়তনের অনুপাত নির্ণয় করাে।

সমাধানঃ

ধরি,

প্রথম লম্ব বৃত্তাকার চোঙের ক্ষেত্রে,

ব্যাসার্ধ = r একক ও উচ্চতা = h একক।

∴ ভূমির পরিধি $=2\pi r$ একক ও আয়তন $=\pi r^{2}h$ ঘন একক।

ধরি,

দ্বিতীয় লম্ব বৃত্তাকার চোঙের ক্ষেত্রে,

ব্যাসার্ধ = R একক ও উচ্চতা = 2h একক।

∴ ভূমির পরিধি $=2\pi R$ একক ও আয়তন $\pi\times R^{2}\times 2h=2\pi R^{2}h$ ঘন একক।

প্রশ্নানুযায়ী,

$\frac{2\pi r}{2\pi R}=\frac{3}{4}$

বা, $\frac{r}{R}=\frac{3}{4}$

লম্ব বৃত্তাকার নিরেট চোঙ দুটির আয়তনের অনুপাত

$=\frac{\pi r^{2}h}{2\pi R^{2}h}$

$=\frac{1}{2}\times \left ( \frac{r}{R} \right )^{2}$

$=\frac{1}{2}\times \left ( \frac{3}{4} \right )^{2}$

$=\frac{1}{2}\times \frac{3}{4}\times \frac{3}{4}$

$=\frac{9}{32}$

$=9:32$

উত্তরঃ নির্ণেয় লম্ব বৃত্তাকার নিরেট চোঙ দুটির আয়তনের অনুপাত 9 : 32

Madhyamik 2022 Math Paper Solution

4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাওঃ (যে কোনাে দশটি) 2 × 10 = 20

(xi) একটি গােলকের ব্যাসার্ধের দৈর্ঘ্য 50% বৃদ্ধি করলে বক্রতলের ক্ষেত্রফল শতকরা কত বৃদ্ধি পায়, তা নির্ণয় করাে।

সমাধানঃ

ধরি,

গােলকটির ব্যাসার্ধ r একক।

∴ গােলকের বক্রতলের ক্ষেত্রফল $=4\pi r^{2}$ বর্গ একক।

এখন গােলকের ব্যাসার্ধের দৈর্ঘ্য 50% বৃদ্ধি করলে নতুন ব্যাসার্ধ হবে $=r+r\times \frac{50}{100}=r+\frac{r}{2}=\frac{3r}{2}$ একক ও বক্রতলের ক্ষেত্রফল হবে $=4\pi \left ( \frac{3r}{2} \right )^{2}=9\pi r^{2}$ বর্গ একক।

∴ বক্রতলের ক্ষেত্রফল শতকরা বৃদ্ধি পায়

$=\frac{9\pi r^{2}-4\pi r^{2}}{4\pi r^{2}}\times 100$

$=\frac{5\pi r^{2}}{4\pi r^{2}}\times 100$

= 125 %

উত্তরঃ নির্ণেয় গোলকটির বক্রতলের ক্ষেত্রফল শতকরা 125 % বৃদ্ধি পায়।

Madhyamik 2022 Math Paper Solution

4. নিম্নলিখিত প্রশ্নগুলির উত্তর দাওঃ (যে কোনাে দশটি) 2 × 10 = 20

(xii) একটি ঘনকের কর্ণের দৈর্ঘ্য $4\sqrt{3}$ সেমি.। ঘনকটির সমগ্রতলের ক্ষেত্রফল নির্ণয় করাে।

সমাধানঃ

ধরি, ঘনকের বাহুর দৈর্ঘ্য = a সেমি.

প্রদত্ত,

ঘনকের কর্ণের দৈর্ঘ্য $4\sqrt{3}$ সেমি.

আবার

আমরা জানি,

ঘনকের কর্ণের দৈর্ঘ্য $=a\sqrt{3}$

বা, $4\sqrt{3}=a\sqrt{3}$

$\therefore a=\frac{4\sqrt{3}}{\sqrt{3}}=4$

∴ ঘনকটির সমগ্রতলের ক্ষেত্রফল

$=6a^{2}=6\times \left ( 4 \right )^{2}=96$ বর্গসেমি.।

উত্তরঃ নির্ণেয় ঘনকটির সমগ্রতলের ক্ষেত্রফল 96 বর্গসেমি.।

Madhyamik 2022 Math Paper Solution

Madhyamik 2020 Math Paper Solution

Madhyamik 2019 Math Paper Solution

Madhyamik 2018 Math Paper Solution

Madhyamik 2017 Math Paper Solution

5. যে কোনাে দুটি প্রশ্নের উত্তর দাও : 5 × 2 = 10

(i) কোনাে মূলধনের একই বার্ষিক শতকরা সরল সুদের হারে 7 বছরে সুদে আসলে 7,100 টাকা এবং 4 বছরে সুদে-আসলে 6,200 টাকা হলে মূলধন ও বার্ষিক শতকরা সরল সুদের হার নির্ণয় করাে।

সমাধানঃ

প্রশ্নানুযায়ী,

আসল + 7 বছরের সুদ = 7100 টাকা…..(i)

আসল + 4 বছরের সুদ = 6200 টাকা…. (ii)

(i) নং সমীকরণ থেকে (ii) নং সমীকরণ বিয়োগ করে পাই ,

∴ 3 বছরের সুদ = 900 টাকা।

∴ 1 বছরের সুদ = $\frac{900}{3}$

⇒ 300 টাকা।

∴ 4 বছরের সুদ = 300 × 4

= 1200 টাকা।

∴ আসল (p) = 4 বছরের সুদ-আসল – 4 বছরের সুদ

= (6200 – 1200) টাকা

= 5000 টাকা ।

সময় (t) = 4 বছর ।

সুদ (I) = 1200 টাকা ।

ধরি, বার্ষিক সুদের হার = r %

আমরা জানি,
$I = \frac{prt}{100}$

$\Rightarrow 1200 = \frac{5000\times r\times 4}{100}$

$\therefore r = \frac{1200\times 100}{5000\times 4}\Rightarrow 6$

∴ r = 6%

উত্তরঃ নির্ণেয় মূলধন 5000 টাকা ও বার্ষিক সরল সুদের হার 6%

Madhyamik 2022 Math Paper Solution

5. যে কোনাে দুটি প্রশ্নের উত্তর দাও : 5 × 2 = 10

(ii) তিনবন্ধু যথাক্রমে 8,000 টাকা, 10,000 টাকা ও 12,000 টাকা সংগ্রহ করে এবং ব্যাঙ্ক থেকে কিছু টাকা ঋণ নিয়ে একটি ব্যবসা শুরু করেন। বছরের শেষে তারা দেখলেন 13,400 টাকা লাভ হয়েছে। সেই লাভ থেকে ব্যাঙ্কের বছরের কিস্তি 5,000 টাকা শােধ দেওয়ার পর বাকি টাকা তারা মূলধনের অনুপাতে ভাগ করে নিলেন। লভ্যাংশ থেকে কে কতাে টাকা পাবেন ?

সমাধানঃ

তিনবন্ধুর মূলধনের অনুপাত

= 8000 : 10000 : 12000

= 8 : 10 : 12

= 4 : 5 : 6

অর্থাৎ, 1ম বন্ধুর মূলধনের অনুপাতিক ভাগহার $=\frac{4}{4+5+6}=\frac{4}{15}$

2য় বন্ধুর মূলধনের অনুপাতিক ভাগহার $=\frac{5}{4+5+6}=\frac{5}{15}$

এবং 3য় বন্ধুর মূলধনের অনুপাতিক ভাগহার $=\frac{6}{4+5+6}=\frac{6}{15}$

বছরের শেষে লাভ হয় 13400 টাকা এবং তা থেকে ব্যাংকে বছরে কিস্তি দিতে হয় 5000 টাকা।

∴ লভ্যাংশের অবশিষ্ট পরিমান

= 13400 টাকা – 5000 টাকা

= 8400 টাকা।

বছরের শেষে লভ্যাংশের অবশিষ্ট পরিমান 8400 টাকা থেকে

1ম বন্ধু পাবে $=8400\times \frac{4}{15}$ টাকা = 2240 টাকা

2য় বন্ধু পাবে $=8400\times \frac{5}{15}$ টাকা = 2800 টাকা ও

3য় বন্ধু পাবে $=8400\times \frac{6}{15}$ টাকা = 3360 টাকা

উত্তরঃ লভ্যাংশ থেকে তিনবন্ধু যথাক্রমে 2240 টাকা, 2800 টাকা এবং 3360 টাকা পাবেন।

Madhyamik 2022 Math Paper Solution

5. যে কোনাে দুটি প্রশ্নের উত্তর দাও : 5 × 2 = 10

(iii) 20,000 টাকার বার্ষিক 5% সুদের হারে, 2 বছরের চক্রবৃদ্ধি সুদ ও সরল সুদের পার্থক্য কত হবে ?

সমাধানঃ

চক্রবৃদ্ধি সুদের ক্ষেত্রে :

প্রদত্ত, আসল (p) = 20000 টাকা,

বার্ষিক চক্রবৃদ্ধি সুদের হার (r) = 5%

সময় (t) = 2 বছর।

আমরা জানি,

t বছর পর সবৃদ্ধিমূল হবে,

$A=p\left ( \frac{100+r}{100} \right )^{t}$

∴ 2 বছর পর সবৃদ্ধিমূল হবে,

$A=20000\left ( \frac{100+5}{100} \right )^{2}$

$=20000\left ( \frac{105}{100} \right )^{2}$

$=20000\times \frac{105\times 105}{100\times 100}$

= 22050 টাকা

∵ চক্রবৃদ্ধি সুদ(I) = সবৃদ্ধিমূল (A) − আসল (p)

বা, I = 22050 টাকা − 20000 টাকা

বা, I = 2050 টাকা

সরল সুদের ক্ষেত্রে :

আমরা জানি,

$I=\frac{prt}{100}$

বা, $I=\frac{20000\times 5\times 2}{100}$

বা, I = 2000 টাকা

∴ এখন, চক্রবৃদ্ধি সুদ ও সরল সুদের অন্তর হবে,

= 2050 টাকা − 2000 টাকা = 50 টাকা

উত্তরঃ নির্ণেয় চক্রবৃদ্ধি সুদ ও সরল সুদের পার্থক্য হবে 50 টাকা।

Madhyamik 2022 Math Paper Solution

6. যে কোনাে দুটি প্রশ্নের সমাধান করাে : 3 × 2 = 6

(i) $\frac{1}{a+b+x}=\frac{1}{a}+\frac{1}{b}+\frac{1}{x}\; x\neq 0,-\left ( a+b \right )$

সমাধানঃ

$\frac{1}{a+b+x}=\frac{1}{a}+\frac{1}{b}+\frac{1}{x}$

$\Rightarrow \frac{1}{a+b+x}-\frac{1}{x}=\frac{1}{a}+\frac{1}{b}$

$\Rightarrow \frac{x-a-b-x}{x\left ( a+b+x \right )}=\frac{b+a}{ab}$

$\Rightarrow \frac{-\left ( a+b \right )}{ax+bx+x^{2}}=\frac{a+b}{ab}$

$\Rightarrow \frac{-1}{ax+bx+x^{2}}=\frac{1}{ab}$

$\Rightarrow ax+bx+x^{2}=-ab$

$\Rightarrow x^{2}+ax+bx+ab=0$

$\Rightarrow x\left ( x+a \right )+b\left ( x+a \right )=0$

$\Rightarrow \left ( x+a \right )\left ( x+b \right )=0$

$\because$ দুটি রাশির গুণফল শূন্য হলে তারা পৃথক পৃথক ভাবে শূন্য হয়,

অর্থাৎ,
$x+a=0$
$\therefore x=-a$

অথবা,
$x+b=0$
$\therefore x=-b$

উত্তরঃ নির্ণেয় দ্বিঘাত সমীকরণের সমাধান ${\color{DarkGreen} -a,-b.}$

Madhyamik 2022 Math Paper Solution

6. যে কোনাে দুটি প্রশ্নের সমাধান করাে : 3 × 2 = 6

(ii) সমীকরণের বীজদ্বয় – 4, 3 হলে দ্বিঘাত সমীকরণটি নির্ণয় করাে।

সমাধানঃ

আমরা জানি, x চলসংখ্যা বিশিষ্ট দ্বিঘাত সমীকরণটি হবে,

x² − (বীজ দুটির যোগফল)x + (বীজ দুটির গুনফল) = 0

সুতরাং, যে দ্বিঘাত সমীকরণের দুটি বীজ −4 ও 3, সেই সমীকরণটি হবে –

$x^{2}-\left \{ \left ( -4 \right )+3 \right \}x+\left \{ \left ( -4 \right )\times 3 \right \}=0$

বা, $x^{2}-\left (-1 \right )x+\left (-12 \right )=0$

∴ $x^{2}+x-12=0$

উত্তরঃ নির্ণেয় দ্বিঘাত সমীকরণটি হল ${\color{DarkGreen} x^{2}+x-12=0}$

অন্যভাবে :

$x=-4$ , $x=3$

বা, $\left ( x+4 \right )=0$ , $\left ( x-3 \right )=0$

সুতরাং, যে দ্বিঘাত সমীকরণের দুটি বীজ −4 ও 3, সেই সমীকরণটি হবে –

$\therefore \left ( x+4 \right )\left ( x-3 \right )=0$

বা, $x^{2}+4x-3x-12=0$

বা, $x^{2}+x-12=0$

উত্তরঃ নির্ণেয় দ্বিঘাত সমীকরণটি হল ${\color{DarkGreen} x^{2}+x-12=0}$

Madhyamik 2022 Math Paper Solution

6. যে কোনাে দুটি প্রশ্নের সমাধান করাে : 3 × 2 = 6

(iii) $m+\frac{1}{m}=\sqrt{3}$ হলে, (a) $m^{2}+\frac{1}{m^{2}}$ এবং (b) $m^{3}+\frac{1}{m^{3}}$ -এদের সরলতম মান নির্ণয় করাে ?

সমাধানঃ

(a) $\fn_cm {{m}^{2}}+\frac{1}{{{m}^{2}}}$

$\fn_cm =\left ( m+\frac{1}{m} \right )^{2}-2\times m\times \frac{1}{m}$

$\fn_cm =\left ( \sqrt{3} \right )^{2}-2\: \: {\color{Blue} \left [ \because m+\frac{1}{m}=\sqrt{3} \right ]}$

$\fn_cm =3-2$

$\fn_cm =1$

উত্তরঃ নির্ণেয় $\fn_cm {\color{DarkGreen} {{m}^{2}}+\frac{1}{{{m}^{2}}}}$ এর সরলতম মান 1

(b) $\fn_cm m^{3}+\frac{1}{m^{3}}$

$\fn_cm =\left ( m+\frac{1}{m} \right )^{3}-3\times m\times \frac{1}{m}\left ( m+\frac{1}{m} \right )$

$\fn_cm =\left ( \sqrt{3} \right )^{3}-3\times \sqrt{3}\: \: {\color{Blue} \left [ \because m+\frac{1}{m}=\sqrt{3} \right ]}$

$\fn_cm =3\sqrt{3}-3\sqrt{3}$

$\fn_cm =0$

উত্তরঃ নির্ণেয় $\fn_cm {\color{DarkGreen} {{m}^{3}}+\frac{1}{{{m}^{3}}}}$ এর সরলতম মান 0

Madhyamik 2022 Math Paper Solution

7. যে কোনাে দুটি প্রশ্নের উত্তর দাও : 3 × 2 = 6

(i) সরলতম মান নির্ণয় করাে : $\frac{\sqrt{5}}{\sqrt{3}+\sqrt{2}}-\frac{3\sqrt{3}}{\sqrt{2}+\sqrt{5}}+\frac{2\sqrt{2}}{\sqrt{3}+\sqrt{5}}$

সমাধানঃ

$\frac{\sqrt{5}}{\sqrt{3}+\sqrt{2}}-\frac{3\sqrt{3}}{\sqrt{2}+\sqrt{5}}+\frac{2\sqrt{2}}{\sqrt{3}+\sqrt{5}}$

$\fn_cm =\frac{\sqrt{5}\left ( \sqrt{3}-\sqrt{2} \right )}{\left ( \sqrt{3}+\sqrt{2} \right )\left ( \sqrt{3}-\sqrt{2} \right )}-\frac{3\sqrt{3}\left ( \sqrt{2}-\sqrt{5} \right )}{\left ( \sqrt{2}+\sqrt{5} \right )\left ( \sqrt{2}-\sqrt{5} \right )}+\frac{2\sqrt{2}\left ( \sqrt{3}-\sqrt{5} \right )}{\left ( \sqrt{3}+\sqrt{5} \right )\left ( \sqrt{3}-\sqrt{5} \right )}$ [হরের করণী নিরসন করে পাই ]

$\fn_cm =\frac{\left ( \sqrt{15}-\sqrt{10} \right )}{\left ( \sqrt{3} \right )^{2}-\left ( \sqrt{2} \right )^{2}}-\frac{3\left ( \sqrt{6}-\sqrt{15} \right )}{\left ( \sqrt{2} \right )^{2}-\left ( \sqrt{5} \right )^{2}}+\frac{2\left ( \sqrt{6}-\sqrt{10} \right )}{\left ( \sqrt{3} \right )^{2}-\left ( \sqrt{5} \right )^{2}}$

$=\frac{\left ( \sqrt{15}-\sqrt{10} \right )}{3-2}-\frac{3\left ( \sqrt{6}-\sqrt{15} \right )}{2-5}+\frac{2\left ( \sqrt{6}-\sqrt{10} \right )}{3-5}$

$=\frac{\left ( \sqrt{15}-\sqrt{10} \right )}{1}-\frac{3\left ( \sqrt{6}-\sqrt{15} \right )}{-3}+\frac{2\left ( \sqrt{6}-\sqrt{10} \right )}{-2}$

$=\sqrt{15}-\sqrt{10}+\sqrt{6}-\sqrt{15}-\sqrt{6}+\sqrt{10}$

= 0

উত্তরঃ নির্ণেয় সরলতম মান 0

Madhyamik 2022 Math Paper Solution

7. যে কোনাে দুটি প্রশ্নের উত্তর দাও : 3 × 2 = 6

(ii) যদি $a=\frac{\sqrt{5}+1}{\sqrt{5}-1}$ এবং ab = 1 হয়, তবে $\left ( \frac{a}{b}+\frac{b}{a} \right )$ –এর মান নির্ণয় করাে।

সমাধানঃ

প্রদত্ত,

$a=\frac{\sqrt{5}+1}{\sqrt{5}-1}$

এবং

ab = 1

বা, $b=\frac{1}{a}$

বা, $\fn_cm b=\frac{\sqrt{5}-1}{\sqrt{5}+1}$

∴ a + b

$\fn_cm =\frac{\sqrt{5}+1}{\sqrt{5}-1}+\frac{\sqrt{5}-1}{\sqrt{5}+1}$

$\fn_cm =\frac{\left ( \sqrt{5}+1 \right )^{2}+\left ( \sqrt{5}-1 \right )^{2}}{\left ( \sqrt{5}-1 \right )\left ( \sqrt{5}+1 \right )}$

$\fn_cm =\frac{2\left [ \left ( \sqrt{5} \right )^{2}+\left ( 1 \right )^{2} \right ]}{\left ( \sqrt{5} \right )^{2}-\left ( 1 \right )^{2}}$ $\fn_cm {\color{Blue}\left [\because \left ( i \right ) \left ( a+b \right )^{2}+\left ( a-b \right )^{2}=2\left (a^{2}+b ^{2} \right ), \left ( ii \right ) \left ( a-b \right )\left ( a+b \right )=a^{2}-b^{2}\right ]}$

$\fn_cm =\frac{2\left ( 5+1 \right )}{\left ( 5-1 \right )}$

$\fn_cm =\frac{2\times 6}{4}$

$\fn_cm =3$

নির্ণেয় ${\color{DarkGreen} \left ( \frac{a}{b}+\frac{b}{a} \right )}$ এর মান

$=\frac{a^{2}+b^{2}}{ab}$

$=\frac{\left ( a+b \right )^{2}-2ab}{ab}$

$=\frac{\left ( 3 \right )^{2}-2\times 1}{1}$

= 9 − 2

= 7 (উত্তর)

Madhyamik 2022 Math Paper Solution

7. যে কোনাে দুটি প্রশ্নের উত্তর দাও : 3 × 2 = 6

(iii) 15 জন কৃষক 5 দিনে 18 বিঘা জমি চাষ করতে পারেন। ভেদতত্ত্ব প্রয়ােগ করে 10 জন কৃষক 12 বিঘা জমি কত দিনে চাষ করতে পারবেন, তা নির্ণয় করাে।

সমাধানঃ

ধরি,

কৃষক সংখ্যা = x জন , সময় = y দিন ও জমির পরিমান = z বিঘা।

জমির পরিমান অপরিবর্তিত থাকলে, কৃষকের সংখ্যা কমলে চাষ করার জন্য প্রয়োজনীয় সময় বেশি লাগবে।

সুতরাং, কৃষক সংখ্যার সাথে সময় ব্যস্ত সম্পর্কে আছে।

অর্থাৎ,

y ∝ $\frac{1}{x}$ , যখন z ধ্রুবক।

আবার,

কৃষকের সংখ্যা অপরিবর্তিত রেখে, জমির পরিমান কমালে, চাষ করার জন্য প্রয়োজনীয় সময় কম লাগবে।

সুতরাং, জমির পরিমানের সাথে সময় সরল সম্পর্কে আছে।

অর্থাৎ,

y ∝ z , যখন x ধ্রুবক।

যৌগিক ভেদের উপপাদ্য অনুযায়ী ,

y ∝ $\frac{z}{x}$

বা, $y=k\times \frac{z}{x}$ [ k = অশূন্য ভেদ ধ্রুবক ]

বা, $k=\frac{xy}{z}$ ……….(i )

(i ) নং সমীকরণে y = 5 , z = 18 এবং x = 15 বসিয়ে পাই,

$k=\frac{15\times 5}{18}$

$\therefore k=\frac{25}{6}$

আবার (i ) নং সমীকরণে x = 10 , z = 12 এবং $k=\frac{25}{6}$ বসিয়ে পাই,

$\frac{25}{6}=\frac{10\times y}{12}$

বা, $y=\frac{25\times 12}{10\times 6}$

$\therefore y=5$

উত্তরঃ 10 জন কৃষক 12 বিঘা জমি 5 দিনে চাষ করতে পারবেন।

Madhyamik 2022 Math Paper Solution

8. যে কোনাে একটি প্রশ্নের উত্তর দাও : 1 × 3 = 3

(i) যদি a : b = b; c হয়, তবে প্রমাণ করাে

$\frac{abc\left ( a+b+c \right )^{3}}{\left ( a+b+c \right )^{3}}=1$

সমাধানঃ

a : b = b : c

বা, $\frac{a}{b}=\frac{b}{c}=k$ (ধরি)

$\therefore b=ck,a=bk=ck\times k=ck^{2}$

বামপক্ষ :

$\frac{abc{{\left( a+b+c \right)}^{3}}}{{{\left( ab+bc+ca \right)}^{3}}}$

a ও b এর মান বসিয়ে পাই,

$=\frac{ck^{2}\times ck\times c\times {{\left( ck^{2}+ck+c \right)}^{3}}}{{{\left( ck^{2}\times ck+ck\times c+c\times ck^{2} \right)}^{3}}}$

$=\frac{c^{3}k^{3}c^{3}{{\left( k^{2}+k+1 \right)}^{3}}}{{{\left( c^{2}k^{3}+c^{2}k+c^{2}k^{2} \right)}^{3}}}$

$=\frac{c^{6}k^{3}{{\left( k^{2}+k+1 \right)}^{3}}}{{{c^{6}k^{3}\left( k^{2}+1+k \right)}^{3}}}$

= 1

= ডানপক্ষ

∴ বামপক্ষ = ডানপক্ষ (প্রমাণিত)

Madhyamik 2022 Math Paper Solution

8. যে কোনাে একটি প্রশ্নের উত্তর দাও : 1 × 3 = 3

(ii) $\frac{a}{1-a}+\frac{b}{1-b}+\frac{c}{1-c}=1$ হলে, $\frac{1}{1-a}+\frac{1}{1-b}+\frac{1}{1-c}$ এর মান নির্ণয় করাে।

সমাধানঃ

$\frac{a}{1-a}+\frac{b}{1-b}+\frac{c}{1-c}=1$

বা, $\frac{a}{1-a}+1+\frac{b}{1-b}+1+\frac{c}{1-c}+1=1+3$

বা, $\frac{a+1-a}{1-a}+\frac{b+1-b}{1-b}+\frac{c+1-c}{1-c}=4$

${\color{DarkGreen} \therefore \frac{1}{1-a}+\frac{1}{1-b}+\frac{1}{1-c} =4}$ (উত্তর)

Madhyamik 2022 Math Paper Solution

9. যে কোনাে একটি প্রশ্নের উত্তর দাও : 1 × 5 = 5

(i) প্রমাণ করাে যে, বৃত্তস্থ চতুর্ভুজের বিপরীত কোণগুলি পরস্পর সম্পূরক।

সমাধানঃ

$madhyamik 2022 math paper solution$

Madhyamik 2022 Math Paper Solution

9. যে কোনাে একটি প্রশ্নের উত্তর দাও : 1 × 5 = 5

(ii) প্রমাণ করাে ব্যাস নয় এরূপ কোনাে জ্যা-এর উপর বৃত্তের কেন্দ্র থেকে লম্ব অঙ্কন করা হলে, ঐ লম্ব জ্যা-টিকে সমদ্বিখণ্ডিত করে।

সমাধানঃ

$madhyamik 2022 math paper solution$

Madhyamik 2022 Math Paper Solution

10. যে কোনাে একটি প্রশ্নের উত্তর দাও : 1 × 3 = 3

(i) ABCD একটি বৃত্তস্থ চতুর্ভুজ। DE জ্যা ∠BDC -এর বহির্দ্বিখণ্ডক। প্রমাণ করাে যে AE (বা বর্ধিত AE) ∠BAC -এর বহির্দ্বিখণ্ডক।

সমাধানঃ

$madhyamik 2022 math paper solution$

বৃত্তস্থ চতুর্ভুজ ABCD -এর ∠BDC -এর বহির্দ্বিখণ্ডক DE জ্যা।

প্রমাণ করতে হবে যে, AE হলো ∠BAC -এর বহির্দ্বিখণ্ডক।

অঙ্কনঃ CD কে Y পর্যন্ত এবং BA কে X পর্যন্ত বর্ধিত করা হল।

প্রমাণঃ বৃত্তস্থ চতুর্ভুজ AEDB থেকে পাই,

∠EAX = ∠EDB — (i) [যেহেতু, বৃত্তস্থ চতুর্ভুজের বহিঃস্থ কোন বিপরীত অন্তঃস্থ কোনের সমান]

আবার যেহেতু, ED হলো ∠BDC -এর বহির্দ্বিখণ্ডক।

∴ ∠EDB = ∠EDY —- (ii)

এখন (i) ও (ii) নং সমীকরণ তুলনা করে পাই,

∠EAX = ∠EDY —-(iii)

আবার, বৃত্তস্থ চতুর্ভুজ ACDE থেকে পাই,

∠EDY = ∠EAC —- (iv) [ যেহেতু, বৃত্তস্থ চতুর্ভুজের বহিঃস্থ কোন বিপরীত অন্তঃস্থ কোনের সমান ]-(ii)

(iii) ও (iv) নং সমীকরণ তুলনা করে পাই,

∠EAX = ∠EAC

অর্থাৎ, EA, ∠BAC -এর বহির্দ্বিখণ্ডক।(প্রমানিত)

Madhyamik 2022 Math Paper Solution

10. যে কোনাে একটি প্রশ্নের উত্তর দাও : 1 × 3 = 3

(ii) O কেন্দ্রীয় একটি বৃত্তের AB ও CD দুটি জা-কে বর্ধিত করলে তারা পরস্পরকে P বিন্দুতে ছেদ করে, প্রমাণ করাে যে, ∠AOC − ∠BOD = 2∠BPC.

সমাধানঃ

বৃত্তস্থ কোণ সম্পর্কিত উপপাদ্য

Madhyamik 2022 Math Paper Solution

11. যে কোনাে একটি প্রশ্নের উত্তর দাও : 1 × 5 = 5

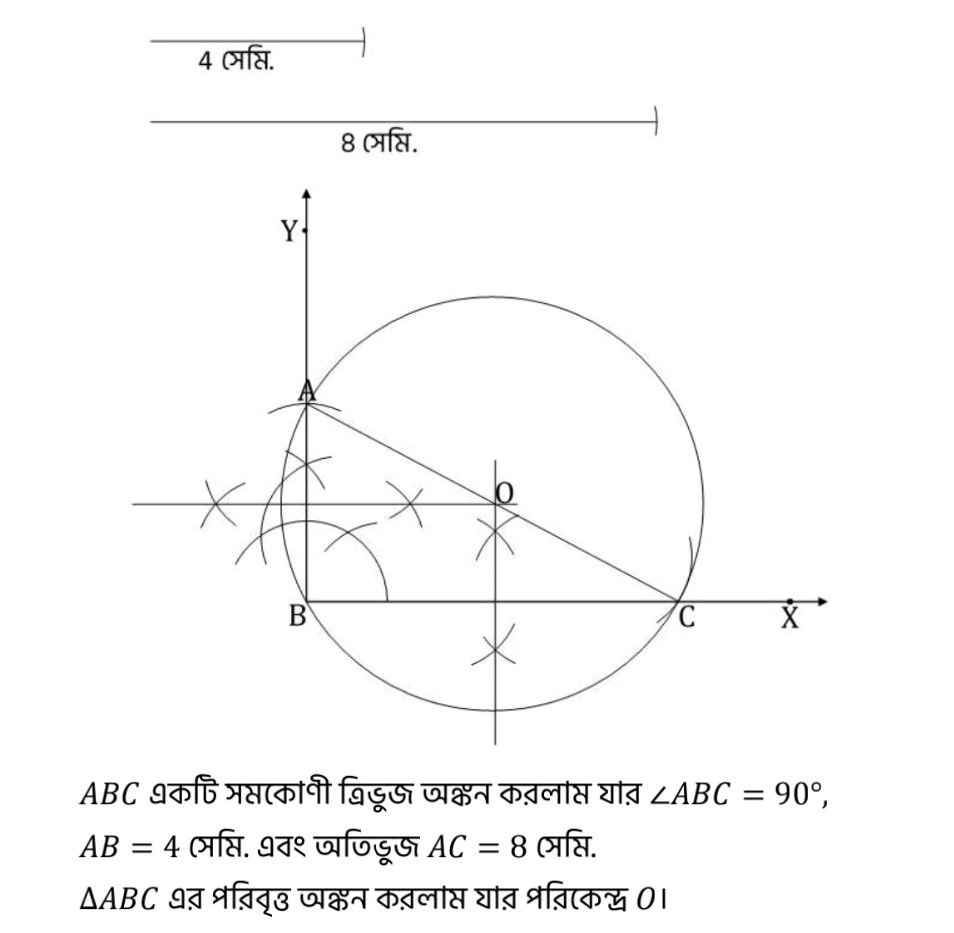
(i) একটি সমকোণী ত্রিভুজ অঙ্কন করাে যার সমকোণ সংলগ্ন বাহুদুটির দৈর্ঘ্য 4 সেমি. ও 8 সেমি.। ত্রিভুজটির পরিবৃত্ত অঙ্কন করাে। (কেবলমাত্র অঙ্কনচিহ্ন দিতে হবে।)

সমাধানঃ

madhyamik 2022 math paper solution

11. যে কোনাে একটি প্রশ্নের উত্তর দাও : 1 × 5 = 5

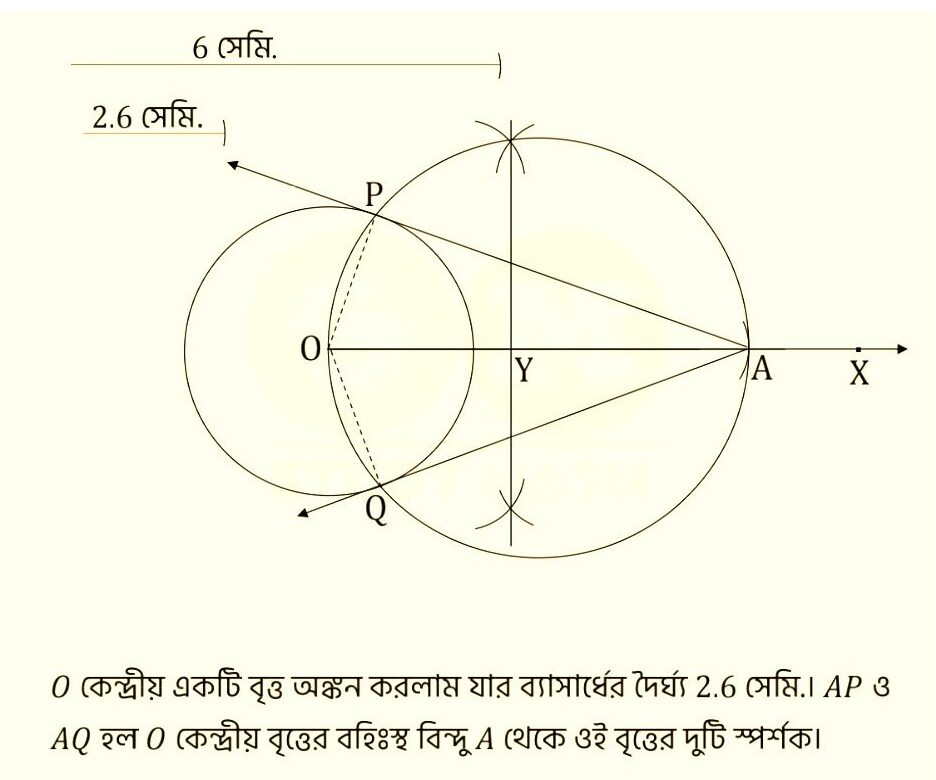
(ii) 2.6 সেমি. দৈর্ঘ্যের ব্যাসার্ধের একটি বৃত্ত অঙ্কন করাে এবং ঐ বৃত্তের কেন্দ্র থেকে 6 সেমি. দূরে, ঐ বৃত্তের বহিঃস্থ কোনাে বিন্দু থেকে বৃত্তটির একটি স্পর্শক অঙ্কন করাে।

সমাধানঃ

madhyamik 2022 math paper

Madhyamik 2022 Math Paper Solution

12. যে কোনাে চারটি প্রশ্নের উত্তর দাও : 4 × 4 = 16

(i) 2.1 মিটার দীর্ঘ, 1.5 মিটার প্রশস্ত একটি আয়তঘনাকার চৌবাচ্চার অর্ধেক জলপূর্ণ আছে। ওই চৌবাচ্চায় আরও 630 লিটার জল ঢাললে জলের উচ্চতা কতটা বৃদ্ধি পাবে নির্ণয় করাে।

সমাধানঃ

ধরি,

আয়তঘনকাকার চৌবাচ্চায় জলের গভীরতা h ডেসিমি বৃদ্ধি পাবে।

প্রদত্ত,

চৌবাচ্চাটির দৈর্ঘ্য (l) = 2.1 মিটার = 21 ডেসিমি. এবং

প্রস্থ (b) = 1.5 মিটার = 15 ডেসিমি.

630 লিটার = 630 ঘন ডেসিমি। [ $\fn_jvn {\color{DarkBlue} \because}$ 1 ঘন ডেসিমি = 1 লিটার ]

প্রশ্নানুসারে,

$\fn_jvn lbh=630$

বা, $\fn_jvn 21\times 15\times h=630$

বা, $\fn_jvn h=\frac{630}{21\times 15}$

$\fn_jvn \therefore h=2$

উত্তরঃ নির্ণেয় আয়তঘনকাকার চৌবাচ্চায় জলের গভীরতা 2 ডেসিমি বৃদ্ধি পাবে।

Madhyamik 2022 Math Paper Solution

12. যে কোনাে চারটি প্রশ্নের উত্তর দাও : 4 × 4 = 16

(ii) একটি লম্ববৃত্তাকার চোঙের উচ্চতা উহার ব্যাসার্ধের দ্বিগুণ। যদি উচ্চতা 6 গুণ হতাে, তবে চোঙটির আয়তন 539 ঘন ডেসিমি. বেশী হতাে, চোঙটির উচ্চতা কত ?

সমাধানঃ

ধরি, লম্ববৃত্তাকার চোঙের ব্যাসার্ধ r ডেসিমি.।

∴ চোঙটির উচ্চতা (h) = 2r ডেসিমিটার।

∴ বর্তমানে চোঙটির আয়তন $=\pi r^{2}h=\pi r^{2}\left ( 2r \right )=2\pi r^{3}$ ঘন ডেসিমি.

আবার,

যদি উচ্চতা 6 গুণ হতো, অর্থাৎ h = 6×r = 6r ডেসিমি.

∴ এখন চোঙটির আয়তন হবে $=\pi r^{2}h=\pi r^{2}\left ( 6r \right )=6\pi r^{3}$ ঘন ডেসিমি.।

প্রশ্নানুসারে,

$2\pi r^{3}+539=6\pi r^{3}$

বা, $539=6\pi r^{3}-2\pi r^{3}$

বা, $539=4\pi r^{3}$

বা, $539=4\times \frac{22}{7}\times r^{3}$

বা, $\frac{539\times 7}{4\times 22}=r^{3}$

বা, $\frac{49\times 7}{4\times 2}=r^{3}$

বা, $\frac{\left ( 7 \right )^{3}}{\left ( 2 \right )^{3}}=r^{3}$

বা, $\left (\frac{7}{2} \right )^{3}=r^{3}$

$\therefore r=\frac{7}{2}$

$\therefore h=2\times \frac{7}{2}=7$

উত্তরঃ নির্ণেয় চোঙটির উচ্চতা 7 ডেসিমিটার।

Madhyamik 2022 Math Paper Solution

Madhyamik 2020 Math Paper Solution

Madhyamik 2019 Math Paper Solution

Madhyamik 2018 Math Paper Solution

Madhyamik 2017 Math Paper Solution

12. যে কোনাে চারটি প্রশ্নের উত্তর দাও : 4 × 4 = 16

(iii) লম্ববৃত্তাকার শঙ্কু আকৃতির একটি তাবুতে 11 জন লােক থাকতে পারে। প্রত্যেক লােকের জন্য ভূমিতে 4 বর্গমিটার জায়গা লাগে এবং 20 ঘনমিটার বাতাসের প্রয়ােজন। ঠিক এই 11 জন লােকের জন্য নির্মিত তাবুর উচ্চতা নির্ণয় করাে।

সমাধানঃ

ধরি, 11 জন লোকের জন্য নির্মিত তাঁবুর উচ্চতা h মিটার।

প্রদত্ত,শঙ্কু আকৃতির তাঁবুতে থাকে 11 জন লোক এবং প্রত্যেক লোকের জন্য ভূমিতে জায়গা লাগে 4 বর্গমিটার এবং 20 ঘনমিটার বাতাসের প্রয়োজন।

∴ শঙ্কু আকৃতির তাঁবুটির ভূমির ক্ষেত্রফল $\left ( \pi r^{2} \right )$ = 4 × 11 বর্গ মিটার = 44 বর্গ মিটার।

ও আয়তন $\left ( \frac{1}{3}\pi r^{2}h \right )$ = 20 × 11 ঘন মিটার = 220 ঘন মিটার।

$\therefore \frac{1}{3}\pi r^{2}h =220$

বা, $\frac{1}{3}\times 44\times h=220$ ${\color{Blue} \left [\because \pi r^{2}=44 \right ]}$

বা, $h=\frac{220\times 3}{44}$

∴ h = 15 মিটার

উত্তরঃ নির্ণেয় 1 জন লোকের জন্য নির্মিত শঙ্কু আকৃতির তাঁবুর উচ্চতা 15 মিটার।

Madhyamik 2022 Math Paper Solution

12. যে কোনাে চারটি প্রশ্নের উত্তর দাও : 4 × 4 = 16

(iv) 8 সেমি. দৈর্ঘ্যের ব্যাসার্ধের একটি নিরেট লােহার গােলককে গলিয়ে 1 সেমি. দৈর্ঘ্যের ব্যাসার্ধের কয়টি নিরেট গােলাকার গুলি তৈরী করা যাবে তা নির্ণয় করাে।

সমাধানঃ

প্রদত্ত,

নিরেট লােহার গােলকের ব্যাসার্ধের দৈর্ঘ্য (R) = 8 সেমি.।

∴ গােলকটির আয়তন $=\frac{4}{3}\pi R^{3}=\frac{4}{3}\pi \times \left ( 8 \right )^{3}$ ঘন সেমি.

এবং গুলিগুলোর প্রত্যেকটির ব্যাসার্ধের দৈর্ঘ্য (r) = 1 সেমি.।

∴ নিরেট গুলির প্রত্যেকটির আয়তন $=\frac{4}{3}\pi r^{3}=\frac{4}{3}\pi \times \left ( 1 \right )^{3}$ ঘন সেমি.

∴ নিরেট গুলির সংখ্যা

= নিরেট লােহার গোলকের আয়তন ÷ নিরেট গুলিগুলোর প্রত্যেকটির আয়তন

$=\frac{\frac{4}{3}\pi \times \left ( 8 \right )^{3}}{\frac{4}{3}\pi \times \left ( 1 \right )^{3}}$

$=\frac{\left (8 \right )^{3}}{\left ( 1 \right )^{3}}$

= 512 টি

উত্তরঃ নিরেট লােহার গােলকটি গলিয়ে 1 সেমি. দৈর্ঘ্যের ব্যাসার্ধের 512 টি নিরেট গুলি তৈরি করা যাবে।

Madhyamik 2022 Math Paper Solution

12. যে কোনাে চারটি প্রশ্নের উত্তর দাও : 4 × 4 = 16

(v) একটি চা-এর বাক্সের ভিতরের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 7.5 ডেসিমি., 6 ডেসিমি. এবং 5.4 ডেসিমি.। চা ভর্তি বাক্সটির ওজন 52 কিগ্রা. 350 গ্রাম। কিন্তু খালি অবস্থায় বাক্সটির ওজন 3.75 কিগ্রা. হলে, 1 ঘন ডেসিমি. চা-এর ওজন কত হবে তা নির্ণয় করাে।

সমাধানঃ

প্রদত্ত,

চা-এর বাক্সের ভেতরের দৈর্ঘ্য, প্রস্থ ও উচ্চতা যথাক্রমে 7.5 ডেসিমি, 6 ডেসিমি এবং 5.4 ডেসিমি।

চা ভর্তি বাক্সটির ওজন 52 কিগ্রা. 350 গ্রাম =52.350 কিগ্রা।

খালি বাক্সটির ওজন 3.75 কিগ্রা।

∴ চা-এর বাক্সের আয়তন

$=7.5\times 6\times 5.4=243$ ঘন ডেসিমি।

বাক্সটির ওজন বাদ দিয়ে শুধুমাত্র 243 ঘন ডেসিমি চা এর ওজন

$=\left ( 52.350-3.75 \right )$ কিগ্রা

$=48.6$ কিগ্রা।

∴ 1 ঘন ডেসিমি. চা-এর ওজন

$=\frac{48.6}{243}$ কিগ্রা

= 0.2 কিগ্রা

= 0.2 × 1000 গ্রাম

= 200 গ্রাম।

উত্তরঃ নির্ণেয় 1 ঘন ডেসিমি. চা-এর ওজন 200 গ্রাম হবে।

Madhyamik 2022 Math Paper Solution

Madhyamik 2022 Math Paper Solution