Koshe dekhi 20.3 Class 8

Koshe dekhi 20.3 Class 8

1. দুজন ব্যক্তির একজন একটি পূর্ব-পশ্চিমমুখী রাস্তায় আসার জন্য দক্ষিণদিক বরাবর আসতে শুরু করলেন এবং অপরজন একই স্থান থেকে একই সাথে দক্ষিণ-পূর্ব দিকে আসতে শুরু করলেন। কোন ব্যক্তি রাস্তায় আগে আসবেন হিসাব করে লিখি।

সমাধানঃ 

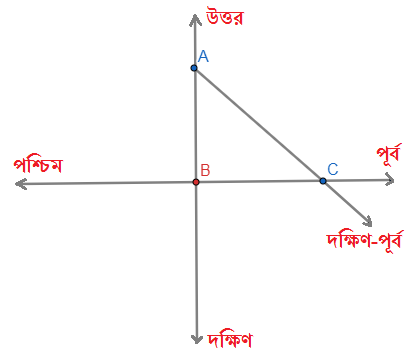
মনে করি, দুইজন ব্যাক্তি A বিন্দু থেকে পূর্ব-পশ্চিমমুখী আসতে শুরু করলেন। একজন \( AB \) বরাবর দক্ষিণদিকে এবং অপর ব্যক্তি \( A C \) বরাবর দক্ষিণপূর্ব দিকে আসতে শুরু করলেন। এখানে \( BC \) হল পূর্ব-পশ্চিমমুখী রাস্তা। দুজন ব্যক্তিকে \(BC \) রেখায় আসতে হলে প্রথম ব্যক্তিকে \( AB \) দূরত্ব এবং দ্বিতীয় ব্যক্তিকে \( AC \) দূরত্ব অতিক্রম করতে হবে।

এখানে, \( A B \perp B C \)
\(\therefore \angle A B C=90° \)

\(\triangle{ABC}\) এর  \(\angle A B C > \angle A C B \)  [\(\because \)  সমকোণ > সুক্ষকোণ] 
\(\therefore \mathrm{AC} > \mathrm{AB} \)

\( \therefore \) প্রথম ব্যক্তি যিনি দক্ষিণমুখী বরাবর আসছেন তিনি আগে পূর্ব-পশ্চিমমুখী রাস্তায় আসবেন।

2. ABCD চতুর্ভুজের  AB = AD  এবং  BC = DC; D  বিন্দু থেকে  AC  বাহুর ক্ষুদ্রতম দূরত্ব  DP; প্রমাণ করি যে  B, P, D  বিন্দু তিনটি সমরেখ।

সমাধানঃ 

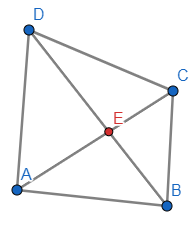
প্রদওঃ \( ABCD \) চতুর্ভুজের \( AB=AD \) এবং \( BC=DC. \)  \( D \) বিন্দু থেকে \( AC \) বাহুর ক্ষুদ্রতম দূরত্ব \( DP \)

প্রামাণ্যঃ \( B, P, D \) বিন্দু তিনটি সমরেখ।

প্রমাণঃ
\( \triangle \mathrm{ABC} \) এবং \( \triangle \mathrm{ADC} \) এর মধ্যে
\( \mathrm{AB}=\mathrm{AD} \) [প্রদত্ত] 
\( \mathrm{BC}=\mathrm{DC} \) [প্রদত্ত] 
\( A C \) সাধারণ বাহু
\( \therefore \triangle \mathrm{ABC} \cong \triangle \mathrm{ADC} \) [সর্বসমতার S-S-S শর্তানুসারে]
\( \therefore \angle B A C=\angle D A C \quad \) [সর্বসম ত্রিভুজের অনুরুপ বাহু ]

\( \triangle \mathrm{ABP} \) এবং \( \triangle \mathrm{ADP} \) এর মধ্যে
\( \mathrm{AB}=\mathrm{AD} \) [প্রদত্ত] 
\( \angle B A P=\angle D A P[\because \angle B A C=\angle D A C] \)
\( AP \)  সাধারণ বাহু 
\( \therefore \triangle \mathrm{ABP} \cong \triangle \mathrm{ADP} \) [সর্বসমতার S-S-S শ শর্তানুসারে]
\( \therefore \angle A P B=\angle A P D \) [সর্বসম ত্রিভুজের অনুরূপ কোণ]

\( D \) বিন্দু থেকে \( AC \) বাহুর ক্ষুদ্রতম দূরত্ব \( DP \)
\(\angle APD=90{}^\circ \)

আবার,
\(\begin{array}{l}\angle APB+\angle APD\\=\angle APD+\angle APD\quad \left[ {\because \angle APB=\angle APD} \right]\\=90{}^\circ +90{}^\circ \\=180{}^\circ \end{array}\)

\( \because \angle A P B \)  ও  \( \angle A P D \) সন্নিহিত কোণ দুটির সমষ্টি \( 180° \)
\( \therefore \quad  B, P, D\) একই সরলরেখায় অবস্থিত।

3. ABC ত্রিভুজের  AD  মধ্যমা। B  ও  C  বিন্দু থেকে  AD  বাহুর ক্ষুদ্রতম দূরত্ব  BP  ও  CQ; প্রমাণ করি যে BP = CQ .

সমাধানঃ 

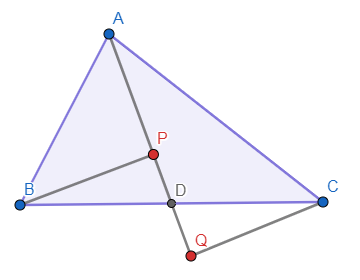
প্রদওঃ \( A B C \) ত্রিভুজের \( A D \) মধ্যমা। \( B \)  ও  \( C \) বিন্দু থেকে \( A D \) বাহুর ক্ষুদ্রতম দূরত্ব \( BP \) ও  \( CQ \)।
প্রামাণ্যঃ \( \mathrm{BP}=\mathrm{CQ} \)
প্রমাণঃ
\( ABC \) ত্রিভুজের \( AD \) মধ্যমা
\( \therefore \mathrm{D}, \mathrm{BC} \) বাহুর মধ্যবিব্দু
\( \therefore B D=C D \) ……(1)

\( \angle B P D=\angle C Q D =90°\) ….. (2)
[ \( B \) ও \(C \) বিন্দু থেকে \( AD \) এর উপর ক্ষুদ্রতম দূরত্ব্ব \( BP \) ও \( CQ \)
\( \therefore B P \perp A D \) এবং \( C Q \perp A D] \)

\( \triangle \mathrm{BDP} \) এবং \( \triangle \mathrm{CDQ} \) এর মধ্যে
\( \angle B P D=\angle C Q D\)   [(1) নং থেকে পাই]
\( \angle B D P= \) বিপ্রতীপ \( \angle C D Q \)
\( \mathrm{BD}=\mathrm{CD} \)   [(2) নং থেকে পাই]

\( \therefore \triangle \mathrm{BDP} \cong \triangle \mathrm{CDQ} \) [সর্বসমতার A-A-S শর্তানুসারে]
\( \therefore B P=C Q \) [সর্বসম ত্রিভুজের অনুরুপ বাহু] [প্রমাণিত]

Koshe Dekhi 20.3 Class 8

and visit Our website : learningscience.co.in 

আরও দেখুনঃ 

গণিত প্রকাশ দশম শ্রেণি – সম্পূর্ণ  সমাধান। 

গণিত প্রকাশ নবম শ্রেণি – সম্পূর্ণ  সমাধান।

গণিত প্রভা অষ্টম শ্রেণি – সম্পূর্ণ সমাধান। 

গণিত প্রভা সপ্তম শ্রেণি – সম্পূর্ণ সমাধান। 

গণিত প্রভা ষষ্ঠ শ্রেণি – সম্পূর্ণ সমাধান। 

জীবন বিজ্ঞান  (দশম শ্রেণী) (Life Science)

Thank You